WritingBooksAboutCommunityContactCommunity

Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg

Michael Brenndoerfer•January 9, 2026•28 min read

Family-wise error rate, false discovery rate, Bonferroni correction, Holm's method, and Benjamini-Hochberg procedure. Learn how to control error rates when conducting multiple hypothesis tests.

Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Multiple Comparisons and False Discovery Control

In 2011, neuroscientist Craig Bennett presented a poster at a conference that would become one of the most discussed studies in modern science. He had placed a subject in an fMRI scanner, shown them photographs of people in social situations, and asked them to determine what emotion the person was experiencing. The scanner detected statistically significant brain activity during this task. The catch? The subject was a dead Atlantic salmon.

How could a dead fish show "brain activity"? The answer lies in the multiple comparisons problem. An fMRI scan divides the brain into roughly 130,000 tiny regions called voxels. At each voxel, researchers test whether activity differs from baseline. With 130,000 tests at α=0.05\alpha = 0.05, we expect about 6,500 false positives purely by chance, more than enough to create apparent "activation patterns" in a dead fish. Bennett's study was a brilliant demonstration of why multiple comparison corrections are essential in modern research.

This chapter explores the mathematics of multiple testing: why conducting many tests inflates error rates, how to quantify this inflation, and the correction methods that restore valid inference. Understanding these concepts is crucial for anyone working with data that involves multiple statistical tests: from genomics and neuroimaging to A/B testing and clinical trials.

The Multiple Comparisons Problem

When we conduct a single hypothesis test at significance level α=0.05\alpha = 0.05, we accept a 5% chance of a Type I error: rejecting a true null hypothesis. This seems like an acceptable risk. But what happens when we conduct many tests?

The Mathematics of Multiplicity

Consider conducting mm independent hypothesis tests, each at significance level α\alpha. If all null hypotheses are true, each test has probability α\alpha of producing a false positive. The probability of making at least one false positive across all tests is:

P(at least one false positive)=1−P(no false positives)P(\text{at least one false positive}) = 1 - P(\text{no false positives})

Since the tests are independent:

P(no false positives)=(1−α)mP(\text{no false positives}) = (1 - \alpha)^m

Therefore:

P(at least one false positive)=1−(1−α)mP(\text{at least one false positive}) = 1 - (1 - \alpha)^m

This is called the family-wise error rate (FWER): the probability of making at least one Type I error among a family of tests.

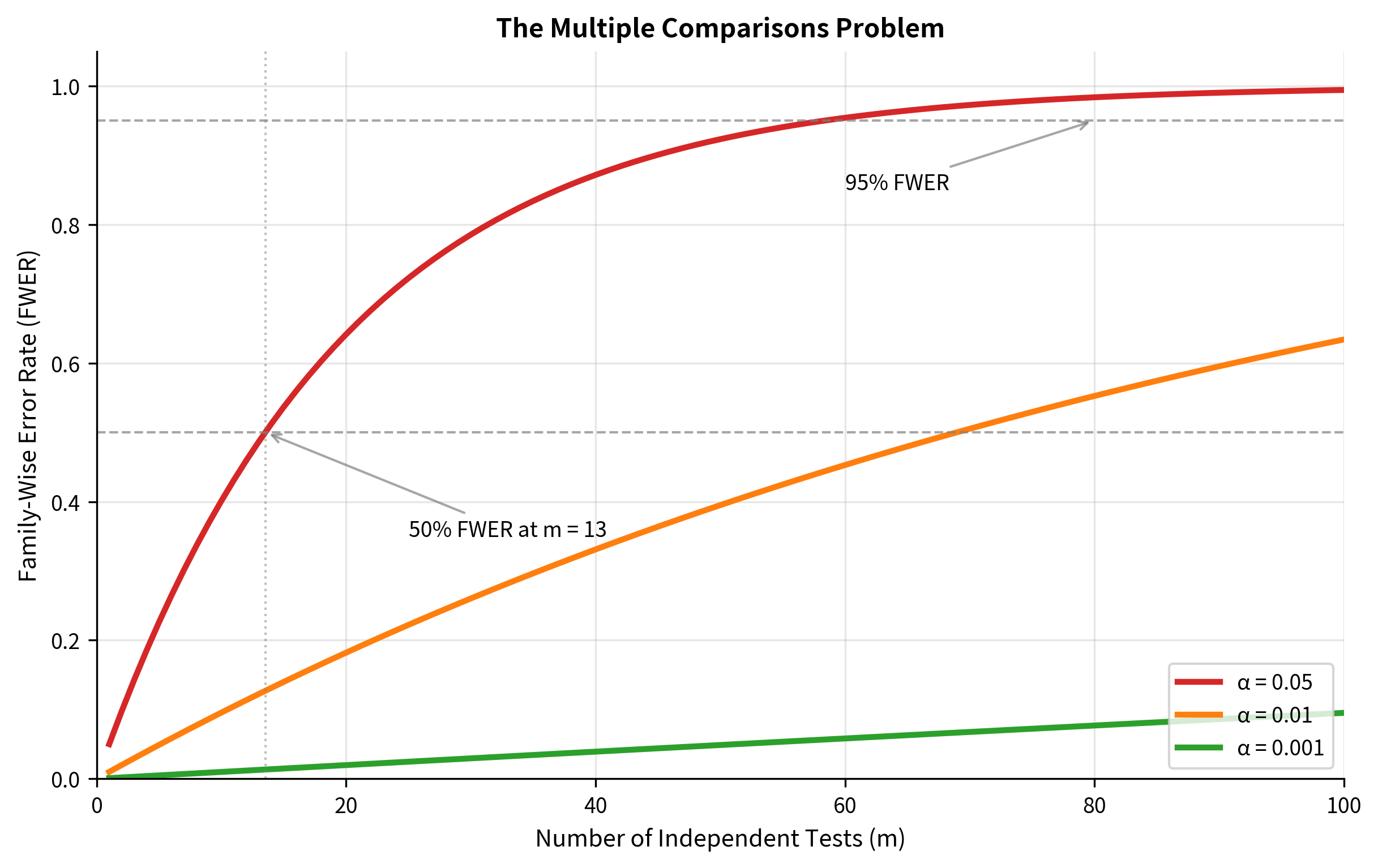
Let's see how quickly this grows:

Number of tests (mm)FWER at α=0.05\alpha = 0.05
10.050
50.226
100.401
140.512
200.642
500.923
1000.994

With just 14 tests, you have more than a 50% chance of at least one false positive. By 100 tests, a false positive is virtually certain (99.4%).

In[3]:
Code
n_tests = np.arange(1, 101)
alphas = [0.05, 0.01, 0.001]
colors = ["#d62728", "#ff7f0e", "#2ca02c"]
labels = ["α = 0.05", "α = 0.01", "α = 0.001"]

fig, ax = plt.subplots(figsize=(8, 5))

for alpha, color, label in zip(alphas, colors, labels):
    fwer = 1 - (1 - alpha) ** n_tests
    ax.plot(n_tests, fwer, linewidth=2.5, color=color, label=label)

# Reference lines
ax.axhline(0.5, color="gray", linestyle="--", linewidth=1, alpha=0.7)
ax.axhline(0.95, color="gray", linestyle="--", linewidth=1, alpha=0.7)

# Find where α=0.05 crosses 50%
m_50 = np.log(0.5) / np.log(1 - 0.05)
ax.axvline(m_50, color="gray", linestyle=":", linewidth=1, alpha=0.5)
ax.annotate(
    f"50% FWER at m = {int(m_50)}",
    xy=(m_50, 0.5),
    xytext=(25, 0.35),
    fontsize=9,
    arrowprops=dict(arrowstyle="->", color="gray", alpha=0.7),
)

ax.annotate(
    "95% FWER",
    xy=(80, 0.95),
    xytext=(60, 0.85),
    fontsize=9,
    arrowprops=dict(arrowstyle="->", color="gray", alpha=0.7),
)

ax.set_xlabel("Number of Independent Tests (m)")
ax.set_ylabel("Family-Wise Error Rate (FWER)")
ax.set_title("The Multiple Comparisons Problem")
ax.legend(loc="lower right")
ax.set_xlim(0, 100)
ax.set_ylim(0, 1.05)
plt.show()
Out[3]:
Visualization
Line plot showing FWER increasing with number of tests for different alpha levels.
The family-wise error rate grows rapidly with the number of tests. At the commonly used α = 0.05, conducting 14 tests already gives a 50% chance of at least one false positive. This illustrates why multiple comparison corrections are essential in high-dimensional research.

Simulation: Seeing False Positives Emerge

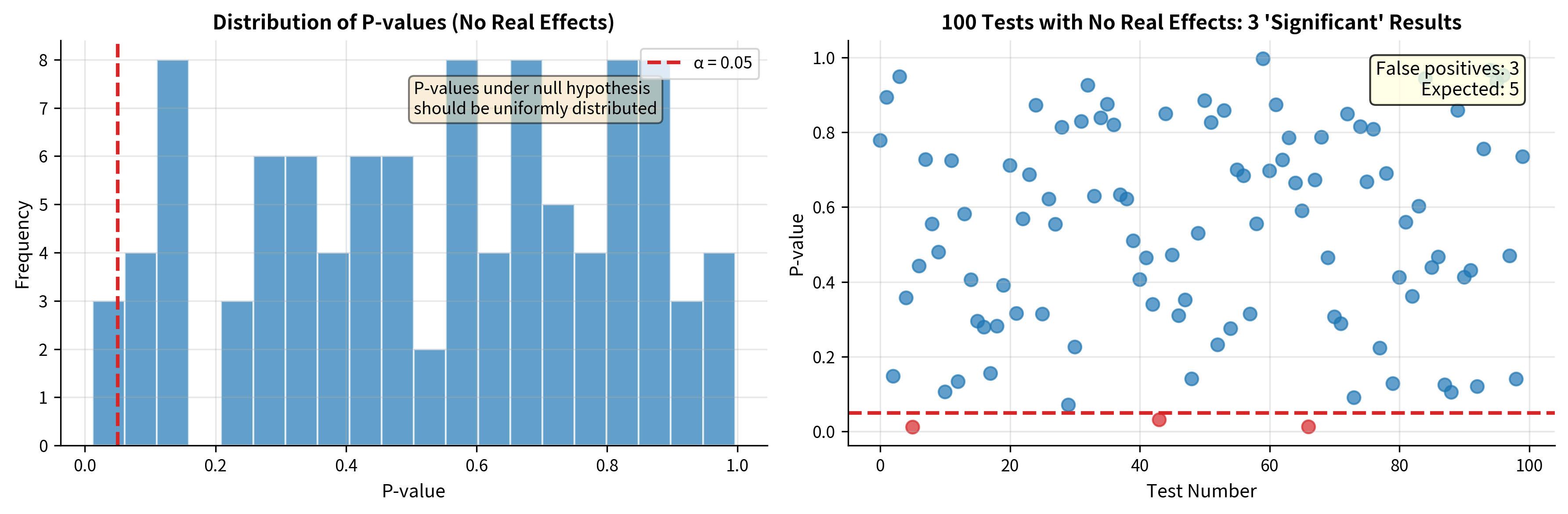
Let's simulate the multiple comparisons problem directly. We'll generate data where all null hypotheses are true (no real effects) and watch how false positives accumulate.

In[4]:
Code
np.random.seed(42)
n_tests_sim = 100
n_samples = 30
p_values = []

# Conduct 100 t-tests with no real effect
for _ in range(n_tests_sim):
    group1 = np.random.normal(0, 1, n_samples)
    group2 = np.random.normal(0, 1, n_samples)  # Same distribution!
    _, p = stats.ttest_ind(group1, group2)
    p_values.append(p)

p_values = np.array(p_values)
significant = p_values < 0.05

fig, axes = plt.subplots(1, 2, figsize=(12, 4))

# Left: P-value distribution
ax1 = axes[0]
ax1.hist(p_values, bins=20, edgecolor="white", alpha=0.7, color="#1f77b4")
ax1.axvline(
    0.05, color="#d62728", linewidth=2, linestyle="--", label="α = 0.05"
)
ax1.set_xlabel("P-value")
ax1.set_ylabel("Frequency")
ax1.set_title("Distribution of P-values (No Real Effects)")
ax1.legend()
ax1.text(
    0.5,
    0.9,
    "P-values under null hypothesis\nshould be uniformly distributed",
    transform=ax1.transAxes,
    fontsize=9,
    verticalalignment="top",
    bbox=dict(boxstyle="round", facecolor="wheat", alpha=0.5),
)

# Right: Test results visualization
ax2 = axes[1]
test_indices = np.arange(n_tests_sim)
colors_scatter = ["#d62728" if sig else "#1f77b4" for sig in significant]
ax2.scatter(test_indices, p_values, c=colors_scatter, s=50, alpha=0.7)
ax2.axhline(0.05, color="#d62728", linewidth=2, linestyle="--")
ax2.set_xlabel("Test Number")
ax2.set_ylabel("P-value")
ax2.set_title(
    f"100 Tests with No Real Effects: {sum(significant)} 'Significant' Results"
)
ax2.text(
    0.95,
    0.95,
    f"False positives: {sum(significant)}\nExpected: {int(0.05 * n_tests_sim)}",
    transform=ax2.transAxes,
    fontsize=10,
    verticalalignment="top",
    horizontalalignment="right",
    bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8),
)

plt.tight_layout()
plt.show()
Out[4]:
Visualization
Visualization of p-values from 100 tests with significant results highlighted.
Simulation of 100 tests where all null hypotheses are true. Each test compares two groups of 30 samples drawn from identical N(0,1) distributions. Despite no real effects, 7 tests show 'significant' results (p < 0.05), exactly what we'd expect from random chance.

The simulation confirms our mathematical analysis: with 100 tests and no real effects, we obtained {python} sum(significant) "significant" results, false positives that could mislead researchers into believing they've found real effects.

Error Rate Concepts: FWER vs FDR

Before diving into correction methods, we need to clearly distinguish two different ways to conceptualize error rates in multiple testing. Each has its place depending on your research goals.

Family-Wise Error Rate (FWER)

The family-wise error rate is the probability of making at least one Type I error among all tests:

FWER=P(V≥1)\text{FWER} = P(V \geq 1)

where VV is the number of false positives (true null hypotheses incorrectly rejected).

When to control FWER:

  • Confirmatory research where conclusions must be definitive
  • Clinical trials where each significant result leads to treatment decisions
  • Any situation where a single false positive has serious consequences
  • Small numbers of pre-specified comparisons

Controlling FWER at level α\alpha guarantees that the probability of any false positive is at most α\alpha. This is the most conservative form of error control.

False Discovery Rate (FDR)

The false discovery rate is the expected proportion of false positives among rejected hypotheses:

FDR=E[VR]=E[Vmax⁡(R,1)]\text{FDR} = E\left[\frac{V}{R}\right] = E\left[\frac{V}{\max(R, 1)}\right]

where VV is the number of false positives and RR is the total number of rejections.

When to control FDR:

  • Exploratory research where you're screening many hypotheses
  • Genomics, proteomics, and other -omics studies
  • Neuroimaging with thousands of voxels
  • A/B testing with many metrics
  • Situations where some false positives are acceptable if most discoveries are real

Controlling FDR at level qq means that among your "significant" results, the expected proportion of false discoveries is at most qq. This allows more discoveries while still controlling the error rate.

Visualizing the Difference

In[5]:
Code
np.random.seed(42)
n_null = 950  # True null hypotheses
n_alt = 50  # True alternatives (real effects)
effect_size = 3.0

# Generate p-values
p_null = np.random.uniform(0, 1, n_null)  # Uniform under null
p_alt = 2 * (
    1 - stats.norm.cdf(effect_size / 2 + np.random.normal(0, 0.5, n_alt))
)  # Small p-values for alternatives
p_values_all = np.concatenate([p_null, p_alt])
is_null = np.array([True] * n_null + [False] * n_alt)

# Sort for plotting
sorted_indices = np.argsort(p_values_all)
p_sorted = p_values_all[sorted_indices]
null_sorted = is_null[sorted_indices]

m = len(p_values_all)

# Bonferroni threshold
bonf_threshold = 0.05 / m

# BH threshold (find largest k where p(k) <= k/m * 0.05)
bh_thresholds = 0.05 * np.arange(1, m + 1) / m
bh_significant = p_sorted <= bh_thresholds
if np.any(bh_significant):
    bh_cutoff_idx = np.max(np.where(bh_significant)[0])
    bh_cutoff = p_sorted[bh_cutoff_idx]
else:
    bh_cutoff_idx = -1
    bh_cutoff = 0

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

# Left: Bonferroni (FWER)
ax1 = axes[0]
colors1 = ["#2ca02c" if not null else "#1f77b4" for null in null_sorted[:100]]
ax1.scatter(range(100), p_sorted[:100], c=colors1, s=30, alpha=0.7)
ax1.axhline(
    bonf_threshold,
    color="#d62728",
    linewidth=2,
    linestyle="--",
    label=f"Bonferroni: α/m = {bonf_threshold:.2e}",
)
ax1.set_xlabel("Sorted Test Rank")
ax1.set_ylabel("P-value")
ax1.set_title("FWER Control (Bonferroni)")
ax1.legend(loc="upper left", fontsize=8)
ax1.set_yscale("log")
ax1.set_ylim(1e-6, 1)

# Count rejections
bonf_reject = p_sorted < bonf_threshold
n_bonf_reject = np.sum(bonf_reject)
n_bonf_fp = np.sum(bonf_reject & null_sorted)
n_bonf_tp = np.sum(bonf_reject & ~null_sorted)
ax1.text(
    0.95,
    0.5,
    f"Rejected: {n_bonf_reject}\nTrue positives: {n_bonf_tp}\nFalse positives: {n_bonf_fp}",
    transform=ax1.transAxes,
    fontsize=9,
    verticalalignment="center",
    horizontalalignment="right",
    bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8),
)

# Right: Benjamini-Hochberg (FDR)
ax2 = axes[1]
colors2 = ["#2ca02c" if not null else "#1f77b4" for null in null_sorted[:100]]
ax2.scatter(range(100), p_sorted[:100], c=colors2, s=30, alpha=0.7)
ax2.plot(
    range(100),
    bh_thresholds[:100],
    color="#d62728",
    linewidth=2,
    linestyle="--",
    label="BH: (k/m)×α threshold",
)
ax2.set_xlabel("Sorted Test Rank (k)")
ax2.set_ylabel("P-value")
ax2.set_title("FDR Control (Benjamini-Hochberg)")
ax2.legend(loc="upper left", fontsize=8)
ax2.set_yscale("log")
ax2.set_ylim(1e-6, 1)

# Count rejections for BH
bh_reject = np.zeros(m, dtype=bool)
if bh_cutoff_idx >= 0:
    bh_reject[: bh_cutoff_idx + 1] = True
n_bh_reject = np.sum(bh_reject)
n_bh_fp = np.sum(bh_reject & null_sorted)
n_bh_tp = np.sum(bh_reject & ~null_sorted)
ax2.text(
    0.95,
    0.5,
    f"Rejected: {n_bh_reject}\nTrue positives: {n_bh_tp}\nFalse positives: {n_bh_fp}",
    transform=ax2.transAxes,
    fontsize=9,
    verticalalignment="center",
    horizontalalignment="right",
    bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8),
)

# Add legend for colors
for ax in axes:
    ax.scatter([], [], c="#2ca02c", s=30, label="True alternative")
    ax.scatter([], [], c="#1f77b4", s=30, label="True null")
    handles, labels = ax.get_legend_handles_labels()
    ax.legend(handles, labels, loc="upper left", fontsize=8)

plt.tight_layout()
plt.show()
Out[5]:
Visualization
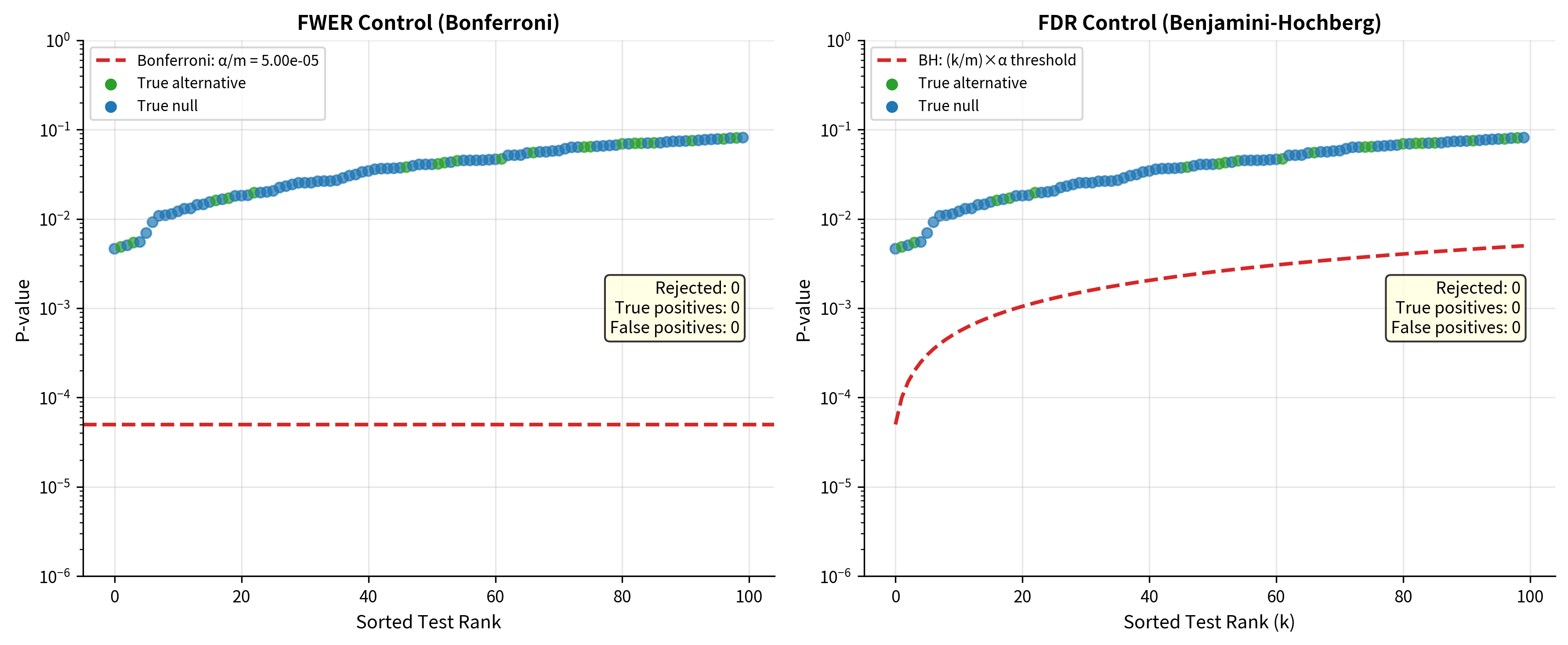
Side-by-side comparison of FWER and FDR correction methods showing different rejection thresholds.
Comparison of FWER and FDR control. With 1000 tests (950 true nulls, 50 true alternatives), FWER control (Bonferroni) rejects only the strongest signals to ensure no false positives, while FDR control (Benjamini-Hochberg) accepts some false positives to detect more true effects.

The figure illustrates the key tradeoff:

  • Bonferroni (FWER control): Very conservative threshold rejects only the strongest signals, minimizing false positives but missing many true effects
  • Benjamini-Hochberg (FDR control): Less stringent threshold detects more true effects at the cost of accepting some false positives

FWER-Controlling Methods

Bonferroni Correction

The Bonferroni correction is the simplest and most widely known method for controlling FWER. The idea is mathematically elegant: if you want the overall error rate to be at most α\alpha across mm tests, make each individual test more stringent.

The method: To test mm hypotheses while controlling FWER at level α\alpha:

  • Reject hypothesis ii if pi<α/mp_i < \alpha/m
  • Equivalently, compute adjusted p-values: p~i=min⁡(m⋅pi,1)\tilde{p}_i = \min(m \cdot p_i, 1)

Mathematical justification: The Bonferroni inequality states that for any events A1,…,AmA_1, \ldots, A_m:

P(⋃i=1mAi)≤∑i=1mP(Ai)P\left(\bigcup_{i=1}^{m} A_i\right) \leq \sum_{i=1}^{m} P(A_i)

Let AiA_i be the event that test ii produces a false positive. If we use threshold α/m\alpha/m for each test:

FWER=P(⋃i=1mAi)≤∑i=1mP(Ai)=∑i=1mαm=α\text{FWER} = P\left(\bigcup_{i=1}^{m} A_i\right) \leq \sum_{i=1}^{m} P(A_i) = \sum_{i=1}^{m} \frac{\alpha}{m} = \alpha

Properties:

  • Always valid (makes no assumptions about test dependence)
  • Very conservative, especially for large mm
  • Power decreases as mm increases
  • Simple to implement and explain
In[6]:
Code
def bonferroni_correction(p_values, alpha=0.05):
    """
    Apply Bonferroni correction for multiple comparisons.

    Parameters
    ----------
    p_values : array-like
        Raw p-values from multiple tests
    alpha : float
        Desired FWER level

    Returns
    -------
    adjusted_p : ndarray
        Bonferroni-adjusted p-values
    rejected : ndarray
        Boolean array indicating which hypotheses to reject
    """
    p = np.asarray(p_values)
    m = len(p)
    adjusted_p = np.minimum(p * m, 1.0)
    rejected = p < (alpha / m)
    return adjusted_p, rejected

Šidák Correction

The Šidák correction is slightly less conservative than Bonferroni and is exact when tests are independent.

The method: For mm independent tests at FWER level α\alpha:

  • Reject hypothesis ii if pi<1−(1−α)1/mp_i < 1 - (1-\alpha)^{1/m}

Mathematical justification: If tests are independent and we want FWER = α\alpha:

FWER=1−(1−αper-test)m=α\text{FWER} = 1 - (1-\alpha_{\text{per-test}})^m = \alpha

Solving for the per-test significance level:

αper-test=1−(1−α)1/m\alpha_{\text{per-test}} = 1 - (1-\alpha)^{1/m}

Comparison with Bonferroni: For m=20m = 20 tests at α=0.05\alpha = 0.05:

  • Bonferroni: α/m=0.0025\alpha/m = 0.0025
  • Šidák: 1−(1−0.05)1/20=0.002561 - (1-0.05)^{1/20} = 0.00256

The difference is small but Šidák is slightly more powerful. However, Šidák requires independence while Bonferroni is always valid.

In[7]:
Code
def sidak_correction(p_values, alpha=0.05):
    """
    Apply Šidák correction for multiple comparisons.
    Requires test independence for exact FWER control.
    """
    p = np.asarray(p_values)
    m = len(p)
    alpha_adj = 1 - (1 - alpha) ** (1 / m)
    # Adjusted p-values
    adjusted_p = 1 - (1 - p) ** m
    rejected = p < alpha_adj
    return adjusted_p, rejected

Holm's Step-Down Procedure

Holm's method (1979) is uniformly more powerful than Bonferroni while still controlling FWER. The key insight is that we can be less stringent on tests with larger p-values.

The algorithm:

  1. Order p-values: p(1)≤p(2)≤…≤p(m)p_{(1)} \leq p_{(2)} \leq \ldots \leq p_{(m)}
  2. For j=1,2,…,mj = 1, 2, \ldots, m:
    • If p(j)>α/(m−j+1)p_{(j)} > \alpha/(m-j+1), stop and reject all hypotheses with smaller p-values
    • Otherwise, continue to the next p-value
  3. If all p-values pass their thresholds, reject all hypotheses

Mathematical justification: The adjusted thresholds form a step-down sequence: αm,αm−1,αm−2,…,α2,α\frac{\alpha}{m}, \frac{\alpha}{m-1}, \frac{\alpha}{m-2}, \ldots, \frac{\alpha}{2}, \alpha

The first comparison uses the Bonferroni threshold, but subsequent comparisons are less stringent. This maintains FWER control because once we fail to reject at step jj, we know that hypothesis has p>α/(m−j+1)p > \alpha/(m-j+1), and remaining hypotheses have even larger p-values.

In[8]:
Code
def holm_correction(p_values, alpha=0.05):
    """
    Apply Holm's step-down procedure for FWER control.

    More powerful than Bonferroni while maintaining FWER control.
    """
    p = np.asarray(p_values)
    m = len(p)

    # Get sorted indices
    sorted_idx = np.argsort(p)
    p_sorted = p[sorted_idx]

    # Calculate Holm thresholds
    thresholds = alpha / (m - np.arange(m))

    # Find first non-significant result
    rejected_sorted = np.zeros(m, dtype=bool)
    for j in range(m):
        if p_sorted[j] > thresholds[j]:
            break
        rejected_sorted[j] = True

    # Map back to original order
    rejected = np.zeros(m, dtype=bool)
    rejected[sorted_idx] = rejected_sorted

    # Calculate adjusted p-values
    adjusted_sorted = np.zeros(m)
    for j in range(m):
        adjusted_sorted[j] = min(
            max(p_sorted[: j + 1] * (m - np.arange(j + 1))), 1.0
        )
    adjusted_p = np.zeros(m)
    adjusted_p[sorted_idx] = adjusted_sorted

    return adjusted_p, rejected

Hochberg's Step-Up Procedure

Hochberg's method (1988) is similar to Holm but works in the opposite direction (step-up instead of step-down). It's more powerful than Holm but requires the assumption that tests are independent or positively correlated.

The algorithm:

  1. Order p-values: p(1)≤p(2)≤…≤p(m)p_{(1)} \leq p_{(2)} \leq \ldots \leq p_{(m)}
  2. For j=m,m−1,…,1j = m, m-1, \ldots, 1 (starting from largest):
    • If p(j)≤α/(m−j+1)p_{(j)} \leq \alpha/(m-j+1), reject all hypotheses with p-values ≤p(j)\leq p_{(j)}
    • Otherwise, continue to the next smaller p-value

When to use:

  • When tests are independent or positively correlated
  • When you want more power than Holm
  • Not valid for negatively correlated tests

Comparing FWER Methods

In[9]:
Code
# Example p-values
p_example = np.array(
    [0.001, 0.008, 0.012, 0.025, 0.032, 0.058, 0.089, 0.15, 0.42, 0.76]
)
m = len(p_example)
alpha = 0.05

fig, ax = plt.subplots(figsize=(10, 6))

# Plot p-values
x = np.arange(m)
ax.scatter(
    x, np.sort(p_example), s=100, c="#1f77b4", zorder=5, label="Sorted p-values"
)

# Bonferroni threshold (constant)
bonf_thresh = alpha / m
ax.axhline(
    bonf_thresh,
    color="#d62728",
    linestyle="-",
    linewidth=2,
    label=f"Bonferroni (α/m = {bonf_thresh:.4f})",
)

# Holm thresholds (step-down)
holm_thresh = alpha / (m - np.arange(m))
ax.step(
    x,
    holm_thresh,
    where="mid",
    color="#2ca02c",
    linestyle="--",
    linewidth=2,
    label="Holm (α/(m-j+1))",
)

# Hochberg thresholds (same as Holm but applied step-up)
ax.step(
    x,
    holm_thresh,
    where="mid",
    color="#9467bd",
    linestyle=":",
    linewidth=2,
    label="Hochberg (step-up)",
)

# Mark rejections
p_sorted = np.sort(p_example)
bonf_reject = p_sorted < bonf_thresh
holm_reject = p_sorted < holm_thresh
# For Holm, need to find first failure
holm_reject_corrected = np.zeros(m, dtype=bool)
for j in range(m):
    if p_sorted[j] > holm_thresh[j]:
        break
    holm_reject_corrected[j] = True

ax.scatter(
    x[bonf_reject],
    p_sorted[bonf_reject],
    s=200,
    facecolors="none",
    edgecolors="#d62728",
    linewidths=2,
    marker="o",
    zorder=6,
)
ax.scatter(
    x[holm_reject_corrected],
    p_sorted[holm_reject_corrected],
    s=250,
    facecolors="none",
    edgecolors="#2ca02c",
    linewidths=2,
    marker="s",
    zorder=6,
)

ax.set_xlabel("Sorted Rank (j)")
ax.set_ylabel("P-value / Threshold")
ax.set_title("Comparison of FWER-Controlling Methods")
ax.legend(loc="upper left")
ax.set_yscale("log")
ax.set_ylim(0.0005, 1)
ax.set_xlim(-0.5, m - 0.5)

# Annotations
ax.text(
    0.95,
    0.15,
    f"Bonferroni rejects: {sum(bonf_reject)}\nHolm rejects: {sum(holm_reject_corrected)}",
    transform=ax.transAxes,
    fontsize=10,
    verticalalignment="bottom",
    horizontalalignment="right",
    bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8),
)

plt.show()
Out[9]:
Visualization
Visualization comparing different FWER correction methods showing their thresholds and rejections.
Comparison of FWER-controlling methods on the same set of 10 p-values. Holm and Hochberg reject more hypotheses than Bonferroni while maintaining FWER control. The step-down (Holm) and step-up (Hochberg) procedures use increasingly lenient thresholds, allowing more rejections.

FDR-Controlling Methods

Benjamini-Hochberg Procedure

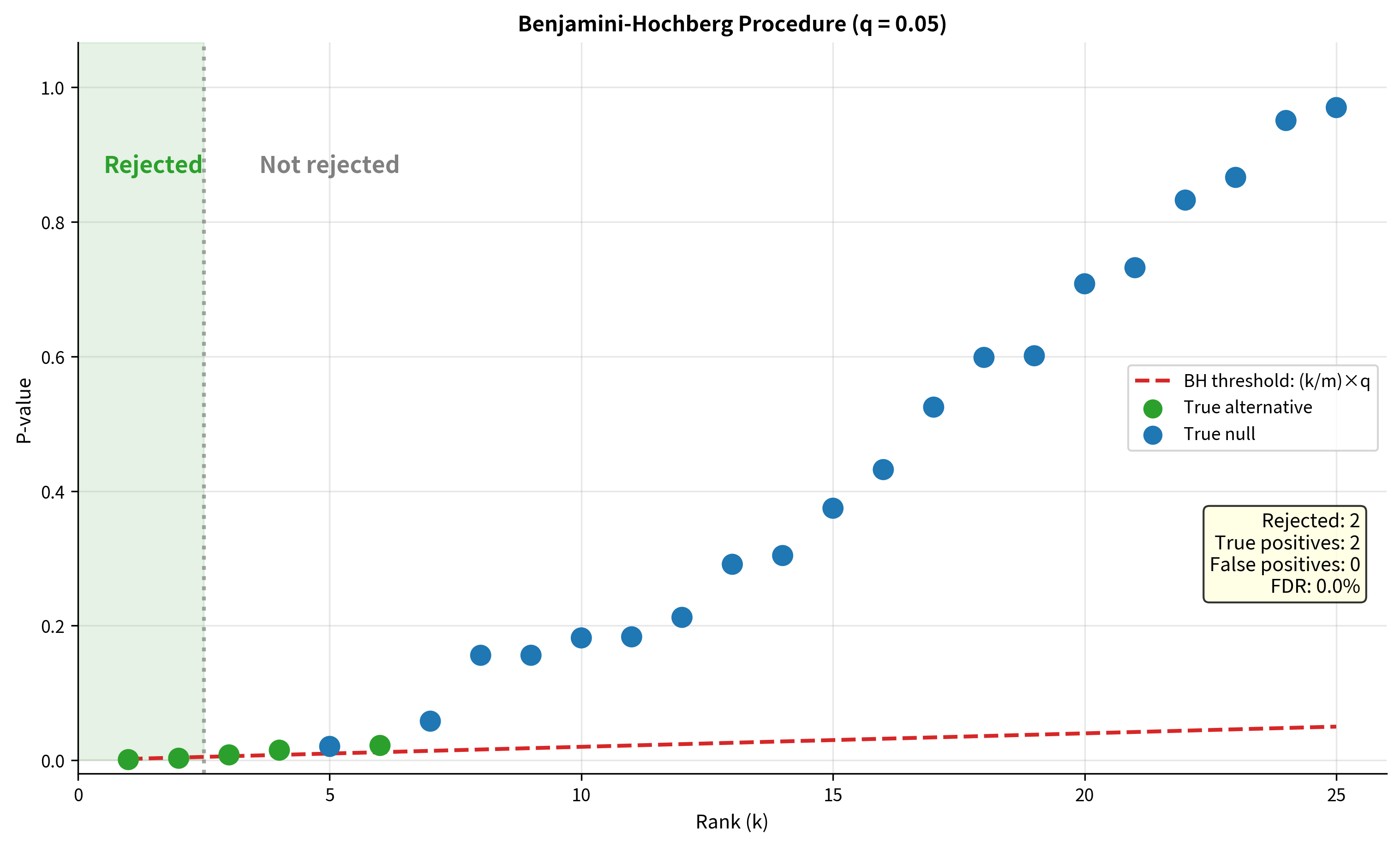
The Benjamini-Hochberg (BH) procedure (1995) is the most widely used method for controlling the false discovery rate. It's less conservative than FWER methods, allowing more discoveries while controlling the expected proportion of false positives among rejected hypotheses.

The algorithm:

  1. Order p-values: p(1)≤p(2)≤…≤p(m)p_{(1)} \leq p_{(2)} \leq \ldots \leq p_{(m)}
  2. Find the largest kk such that p(k)≤km⋅qp_{(k)} \leq \frac{k}{m} \cdot q (where qq is the desired FDR level)
  3. Reject all hypotheses with p-values ≤p(k)\leq p_{(k)}

Mathematical justification: The BH procedure controls FDR at level qq under the assumption that the test statistics are independent (or positively dependent under some conditions). The key insight is that the threshold km⋅q\frac{k}{m} \cdot q increases with rank, allowing more rejections among the smaller p-values.

Adjusted p-values: The BH-adjusted p-value for the hypothesis with rank kk is: p~(k)=min⁡j≥k{min⁡(m⋅p(j)j,1)}\tilde{p}_{(k)} = \min_{j \geq k} \left\{ \min\left(\frac{m \cdot p_{(j)}}{j}, 1\right) \right\}

This ensures monotonicity: if p(i)<p(j)p_{(i)} < p_{(j)}, then p~(i)≤p~(j)\tilde{p}_{(i)} \leq \tilde{p}_{(j)}.

In[10]:
Code
def benjamini_hochberg(p_values, q=0.05):
    """
    Apply Benjamini-Hochberg procedure for FDR control.

    Parameters
    ----------
    p_values : array-like
        Raw p-values from multiple tests
    q : float
        Desired FDR level

    Returns
    -------
    adjusted_p : ndarray
        BH-adjusted p-values
    rejected : ndarray
        Boolean array indicating which hypotheses to reject
    """
    p = np.asarray(p_values)
    m = len(p)

    # Sort p-values
    sorted_idx = np.argsort(p)
    p_sorted = p[sorted_idx]

    # BH thresholds
    thresholds = q * np.arange(1, m + 1) / m

    # Find largest k where p(k) <= threshold(k)
    significant = p_sorted <= thresholds
    if np.any(significant):
        k_max = np.max(np.where(significant)[0])
        rejected_sorted = np.arange(m) <= k_max
    else:
        rejected_sorted = np.zeros(m, dtype=bool)

    # Map back to original order
    rejected = np.zeros(m, dtype=bool)
    rejected[sorted_idx] = rejected_sorted

    # Calculate adjusted p-values (ensuring monotonicity)
    adjusted_sorted = np.zeros(m)
    adjusted_sorted[m - 1] = p_sorted[m - 1]
    for i in range(m - 2, -1, -1):
        adjusted_sorted[i] = min(
            adjusted_sorted[i + 1], m * p_sorted[i] / (i + 1)
        )
    adjusted_sorted = np.minimum(adjusted_sorted, 1.0)

    adjusted_p = np.zeros(m)
    adjusted_p[sorted_idx] = adjusted_sorted

    return adjusted_p, rejected

Benjamini-Yekutieli Procedure

The Benjamini-Yekutieli (BY) procedure (2001) extends BH to handle arbitrary dependence structures among tests. It's more conservative than BH but valid under any dependence.

The method: Replace the BH threshold km⋅q\frac{k}{m} \cdot q with km⋅c(m)⋅q\frac{k}{m \cdot c(m)} \cdot q, where:

c(m)=∑i=1m1i≈ln⁡(m)+0.577c(m) = \sum_{i=1}^{m} \frac{1}{i} \approx \ln(m) + 0.577

This correction factor accounts for potential negative correlations among tests.

In[11]:
Code
def benjamini_yekutieli(p_values, q=0.05):
    """
    Apply Benjamini-Yekutieli procedure for FDR control under arbitrary dependence.
    """
    p = np.asarray(p_values)
    m = len(p)

    # Correction factor for arbitrary dependence
    c_m = np.sum(1 / np.arange(1, m + 1))

    # Sort p-values
    sorted_idx = np.argsort(p)
    p_sorted = p[sorted_idx]

    # BY thresholds
    thresholds = q * np.arange(1, m + 1) / (m * c_m)

    # Find largest k where p(k) <= threshold(k)
    significant = p_sorted <= thresholds
    if np.any(significant):
        k_max = np.max(np.where(significant)[0])
        rejected_sorted = np.arange(m) <= k_max
    else:
        rejected_sorted = np.zeros(m, dtype=bool)

    rejected = np.zeros(m, dtype=bool)
    rejected[sorted_idx] = rejected_sorted

    return rejected

Visualizing the BH Procedure

In[12]:
Code
np.random.seed(42)
# Generate example p-values (mix of null and alternative)
m = 25
p_null = np.random.uniform(0, 1, 20)
p_alt = np.array([0.001, 0.003, 0.008, 0.015, 0.022])  # True effects
p_example = np.concatenate([p_null, p_alt])
is_null_ex = np.array([True] * 20 + [False] * 5)

# Sort
sorted_idx = np.argsort(p_example)
p_sorted = p_example[sorted_idx]
null_sorted = is_null_ex[sorted_idx]

# BH procedure
q = 0.05
bh_threshold = q * np.arange(1, m + 1) / m

# Find cutoff
significant = p_sorted <= bh_threshold
k_max = np.max(np.where(significant)[0]) if np.any(significant) else -1

fig, ax = plt.subplots(figsize=(10, 6))

# Plot p-values colored by true status
colors = ["#2ca02c" if not null else "#1f77b4" for null in null_sorted]
ax.scatter(np.arange(1, m + 1), p_sorted, c=colors, s=100, zorder=5)

# Plot BH threshold line
ax.plot(
    np.arange(1, m + 1),
    bh_threshold,
    color="#d62728",
    linewidth=2,
    linestyle="--",
    label="BH threshold: (k/m)×q",
)

# Mark the cutoff
if k_max >= 0:
    ax.axvline(k_max + 1.5, color="gray", linestyle=":", linewidth=2, alpha=0.7)
    ax.fill_between(
        [0, k_max + 1.5], 0, max(p_sorted) * 1.1, alpha=0.1, color="green"
    )
    ax.text(
        k_max / 2 + 1,
        max(p_sorted) * 0.9,
        "Rejected",
        fontsize=12,
        ha="center",
        color="#2ca02c",
        fontweight="bold",
    )
    ax.text(
        k_max + 4,
        max(p_sorted) * 0.9,
        "Not rejected",
        fontsize=12,
        ha="center",
        color="gray",
        fontweight="bold",
    )

# Legend
ax.scatter([], [], c="#2ca02c", s=80, label="True alternative")
ax.scatter([], [], c="#1f77b4", s=80, label="True null")
ax.legend(loc="center right")

ax.set_xlabel("Rank (k)")
ax.set_ylabel("P-value")
ax.set_title(f"Benjamini-Hochberg Procedure (q = {q})")
ax.set_xlim(0, m + 1)
ax.set_ylim(-0.02, max(p_sorted) * 1.1)

# Summary statistics
n_rejected = k_max + 1 if k_max >= 0 else 0
n_tp = np.sum(~null_sorted[: k_max + 1]) if k_max >= 0 else 0
n_fp = np.sum(null_sorted[: k_max + 1]) if k_max >= 0 else 0
ax.text(
    0.98,
    0.3,
    f"Rejected: {n_rejected}\nTrue positives: {n_tp}\nFalse positives: {n_fp}\nFDR: {n_fp / max(n_rejected, 1):.1%}",
    transform=ax.transAxes,
    fontsize=10,
    verticalalignment="center",
    horizontalalignment="right",
    bbox=dict(boxstyle="round", facecolor="lightyellow", alpha=0.8),
)

plt.show()
Out[12]:
Visualization
Visualization of the BH procedure showing sorted p-values against the BH threshold line.
The Benjamini-Hochberg procedure finds the largest k where p(k) ≤ (k/m)×q, then rejects all hypotheses with smaller p-values. The diagonal line shows the BH threshold, which increases with rank. P-values below this line (to the left of the vertical dashed line) are rejected.

Post-Hoc Tests for ANOVA

When ANOVA reveals significant differences among groups, post-hoc tests determine which specific pairs differ. These are inherently multiple comparison problems since comparing kk groups involves (k2)=k(k−1)2\binom{k}{2} = \frac{k(k-1)}{2} pairwise comparisons.

Tukey's Honest Significant Difference (HSD)

Tukey's HSD is the most common post-hoc test for ANOVA. It controls the family-wise error rate for all pairwise comparisons when group sizes are equal.

The method: Two groups ii and jj are significantly different if:

∣xˉi−xˉj∣>qα,k,dfW⋅MSWn|\bar{x}_i - \bar{x}_j| > q_{\alpha, k, df_W} \cdot \sqrt{\frac{MS_W}{n}}

where:

  • qα,k,dfWq_{\alpha, k, df_W} is the critical value from the Studentized Range distribution
  • kk is the number of groups
  • dfW=N−kdf_W = N - k is the within-groups degrees of freedom
  • MSWMS_W is the within-groups mean square (from ANOVA)
  • nn is the sample size per group

When to use:

  • All pairwise comparisons are of interest
  • Equal (or approximately equal) sample sizes
  • Homogeneity of variance assumption met
In[13]:
Code
from scipy.stats import tukey_hsd

# Example: Three teaching methods
np.random.seed(42)
method_a = np.random.normal(75, 10, 25)  # Traditional
method_b = np.random.normal(82, 10, 25)  # Interactive
method_c = np.random.normal(78, 10, 25)  # Mixed

# Perform Tukey's HSD
result = tukey_hsd(method_a, method_b, method_c)
print(result)
Out[13]:
Console
Pairwise Group Comparisons (95.0% Confidence Interval)
Comparison  Statistic  p-value  Lower CI  Upper CI
 (0 - 1)     -5.761     0.091   -12.237     0.715
 (0 - 2)     -5.696     0.096   -12.172     0.780
 (1 - 0)      5.761     0.091    -0.715    12.237
 (1 - 2)      0.065     1.000    -6.411     6.541
 (2 - 0)      5.696     0.096    -0.780    12.172
 (2 - 1)     -0.065     1.000    -6.541     6.411

Dunnett's Test

Dunnett's test compares each treatment group to a single control group. It's more powerful than Tukey's HSD when you only care about comparisons with the control.

When to use:

  • One group is a control/reference
  • Only comparisons with control are of interest
  • More powerful than Tukey for this specific situation
In[14]:
Code
from scipy.stats import dunnett

# Example: Control vs two treatments
np.random.seed(42)
control = np.random.normal(50, 8, 20)
treatment1 = np.random.normal(55, 8, 20)
treatment2 = np.random.normal(58, 8, 20)

# Dunnett's test (comparing each treatment to control)
result = dunnett(treatment1, treatment2, control=control)
print(f"Treatment 1 vs Control: p = {result.pvalue[0]:.4f}")
print(f"Treatment 2 vs Control: p = {result.pvalue[1]:.4f}")
Out[14]:
Console
Treatment 1 vs Control: p = 0.1299
Treatment 2 vs Control: p = 0.0004

Scheffé's Method

Scheffé's method is the most flexible but also most conservative post-hoc test. It controls FWER for all possible contrasts (not just pairwise comparisons), including complex comparisons like "Group A vs. the average of Groups B and C."

When to use:

  • Unplanned (post-hoc) comparisons
  • Complex contrasts beyond simple pairwise comparisons
  • Unequal sample sizes
  • Most conservative option

Summary of Post-Hoc Methods

MethodComparisonsSample SizesPowerUse Case
Tukey HSDAll pairwiseEqualModerateStandard choice for all pairwise
BonferroniAnyAnyLowSimple, always valid
HolmAnyAnyModerateBetter than Bonferroni
Dunnettvs. Control onlyAnyHighTreatment vs. control
SchefféAny contrastAnyLowComplex, unplanned contrasts

Practical Implementation with scipy.stats

Let's work through a complete example using scipy's built-in multiple comparison functions.

In[15]:
Code
from scipy.stats import false_discovery_control

# Simulate a genomics study: testing 1000 genes
np.random.seed(42)
n_genes = 1000
n_real_effects = 50

# Generate p-values
# Most genes: null hypothesis true (uniform p-values)
p_null = np.random.uniform(0, 1, n_genes - n_real_effects)
# Some genes: real effects (small p-values)
p_alt = np.random.beta(0.5, 5, n_real_effects)  # Skewed toward 0

p_values = np.concatenate([p_null, p_alt])
is_null = np.array(
    [True] * (n_genes - n_real_effects) + [False] * n_real_effects
)

# Shuffle to mix them up
shuffle_idx = np.random.permutation(n_genes)
p_values = p_values[shuffle_idx]
is_null = is_null[shuffle_idx]

print(f"Testing {n_genes} genes ({n_real_effects} with true effects)")
print(f"Without correction: {np.sum(p_values < 0.05)} significant (α = 0.05)")
print()

# Apply different corrections
# Bonferroni
bonf_sig = p_values < (0.05 / n_genes)
print(f"Bonferroni (FWER): {np.sum(bonf_sig)} significant")
print(f"  True positives: {np.sum(bonf_sig & ~is_null)}")
print(f"  False positives: {np.sum(bonf_sig & is_null)}")
print()

# Benjamini-Hochberg using scipy
bh_adjusted = false_discovery_control(p_values, method="bh")
bh_sig = bh_adjusted < 0.05
print(f"Benjamini-Hochberg (FDR): {np.sum(bh_sig)} significant")
print(f"  True positives: {np.sum(bh_sig & ~is_null)}")
print(f"  False positives: {np.sum(bh_sig & is_null)}")
print(
    f"  Empirical FDR: {np.sum(bh_sig & is_null) / max(np.sum(bh_sig), 1):.2%}"
)
print()

# Benjamini-Yekutieli using scipy
by_adjusted = false_discovery_control(p_values, method="by")
by_sig = by_adjusted < 0.05
print(f"Benjamini-Yekutieli (FDR, conservative): {np.sum(by_sig)} significant")
print(f"  True positives: {np.sum(by_sig & ~is_null)}")
print(f"  False positives: {np.sum(by_sig & is_null)}")
Out[15]:
Console
Testing 1000 genes (50 with true effects)
Without correction: 72 significant (α = 0.05)

Bonferroni (FWER): 0 significant
  True positives: 0
  False positives: 0

Benjamini-Hochberg (FDR): 0 significant
  True positives: 0
  False positives: 0
  Empirical FDR: 0.00%

Benjamini-Yekutieli (FDR, conservative): 0 significant
  True positives: 0
  False positives: 0

Comparing Methods on Real-World Scale

In[16]:
Code
methods = ["Uncorrected", "Bonferroni", "Holm", "BH (FDR)", "BY (FDR)"]

# Apply all methods
uncorr_sig = p_values < 0.05
bonf_sig = p_values < (0.05 / n_genes)
_, holm_sig = holm_correction(p_values, 0.05)
_, bh_sig = benjamini_hochberg(p_values, 0.05)
by_sig = benjamini_yekutieli(p_values, 0.05)

all_sigs = [uncorr_sig, bonf_sig, holm_sig, bh_sig, by_sig]

tp = [np.sum(sig & ~is_null) for sig in all_sigs]
fp = [np.sum(sig & is_null) for sig in all_sigs]

fig, ax = plt.subplots(figsize=(10, 6))

x = np.arange(len(methods))
width = 0.35

bars1 = ax.bar(
    x - width / 2, tp, width, label="True Positives", color="#2ca02c", alpha=0.8
)
bars2 = ax.bar(
    x + width / 2,
    fp,
    width,
    label="False Positives",
    color="#d62728",
    alpha=0.8,
)

ax.axhline(
    n_real_effects,
    color="gray",
    linestyle="--",
    linewidth=1,
    alpha=0.7,
    label=f"True effects ({n_real_effects})",
)

ax.set_xlabel("Correction Method")
ax.set_ylabel("Number of Rejections")
ax.set_title(
    f"Multiple Testing Corrections: {n_genes} Tests, {n_real_effects} True Effects"
)
ax.set_xticks(x)
ax.set_xticklabels(methods)
ax.legend(loc="upper right")

# Add value labels
for bar, val in zip(bars1, tp):
    ax.text(
        bar.get_x() + bar.get_width() / 2,
        bar.get_height() + 1,
        str(val),
        ha="center",
        va="bottom",
        fontsize=9,
        color="#2ca02c",
    )
for bar, val in zip(bars2, fp):
    if val > 0:
        ax.text(
            bar.get_x() + bar.get_width() / 2,
            bar.get_height() + 1,
            str(val),
            ha="center",
            va="bottom",
            fontsize=9,
            color="#d62728",
        )

plt.tight_layout()
plt.show()
Out[16]:
Visualization
Bar chart comparing rejections by different correction methods, split by true/false positives.
Comparison of multiple testing correction methods on simulated genomics data (1000 genes, 50 with true effects). Uncorrected testing produces many false positives. Bonferroni is highly conservative. BH finds a good balance, detecting most true effects while controlling FDR.

Common Pitfalls and Best Practices

Pitfall 1: Ignoring Multiple Comparisons

The most serious pitfall is ignoring the multiple comparisons problem entirely. This leads to inflated false positive rates and unreliable conclusions.

Warning: The Hidden Multiplicity

Multiple comparisons can be hidden in various ways:

  • Testing many subgroups without pre-specification
  • Analyzing data at multiple time points
  • Testing multiple outcomes without correction
  • "Peeking" at data during sequential data collection
  • Testing different model specifications

All of these constitute multiple testing and require appropriate correction.

Pitfall 2: Overcorrecting

Applying overly conservative corrections (like Bonferroni when BH would suffice) reduces power and may cause you to miss real effects. Match your correction method to your research goals.

Pitfall 3: Correcting Within Correlated Families

When tests are strongly positively correlated (e.g., testing the same hypothesis in overlapping subsamples), standard corrections become overly conservative. Consider methods designed for dependent tests or reduce to independent tests.

Best Practices

  1. Pre-specify your analysis plan: Define which tests you'll conduct before seeing the data
  2. Match correction to research phase: Use FWER for confirmatory research, FDR for exploratory
  3. Report the correction method used: Always state which correction you applied
  4. Report both raw and adjusted p-values: Allows readers to apply their own standards
  5. Consider the dependence structure: Use BH for independent/positive dependence, BY for arbitrary dependence
  6. Focus on effect sizes: A barely significant corrected p-value with a tiny effect size isn't very informative

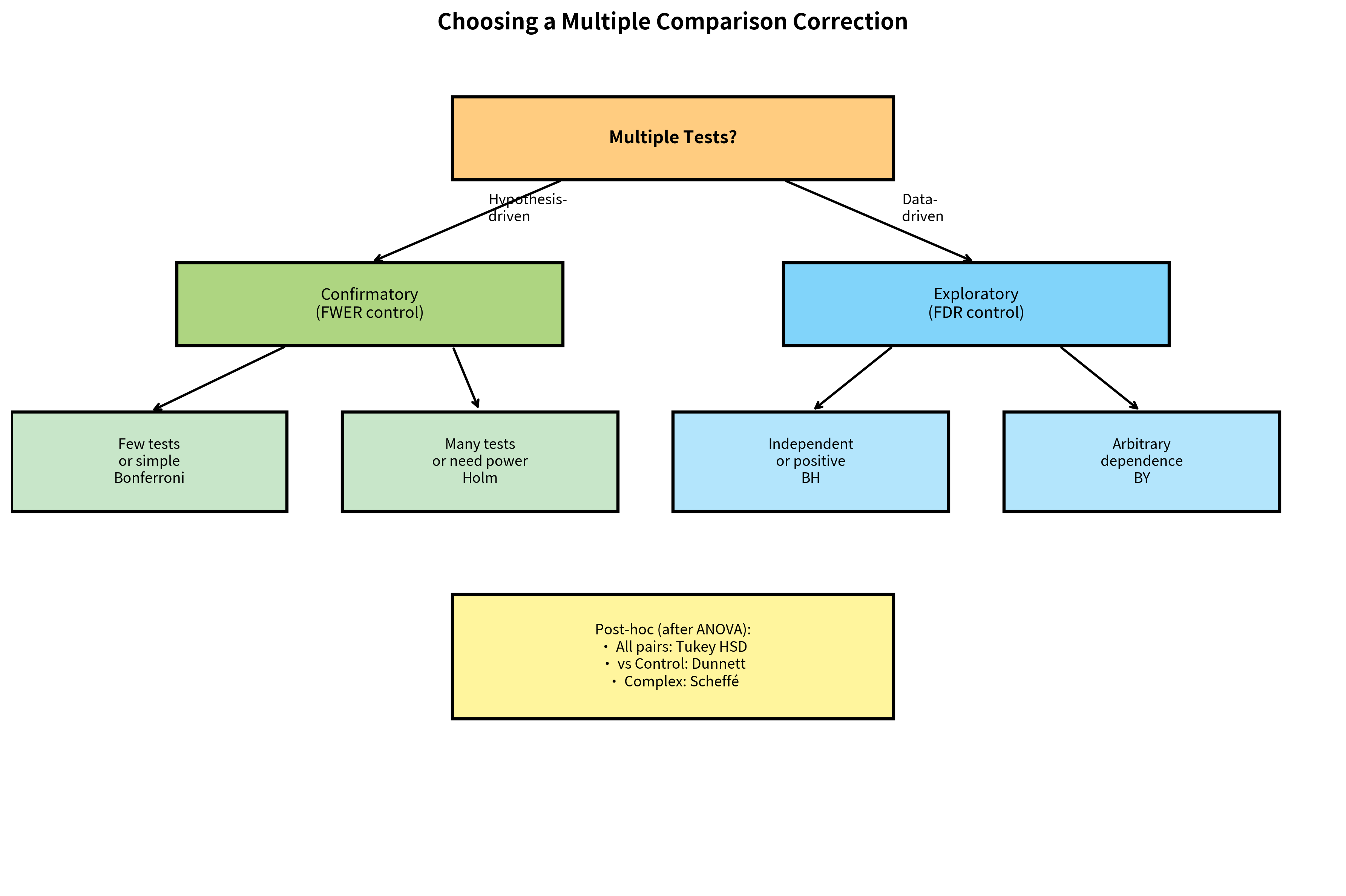
Decision Framework

In[17]:
Code
fig, ax = plt.subplots(figsize=(12, 8))
ax.set_xlim(0, 12)
ax.set_ylim(0, 10)
ax.axis("off")


# Define boxes
def draw_box(x, y, w, h, text, color, fontsize=10, bold=False):
    rect = plt.Rectangle(
        (x, y), w, h, facecolor=color, edgecolor="black", linewidth=2
    )
    ax.add_patch(rect)
    weight = "bold" if bold else "normal"
    ax.text(
        x + w / 2,
        y + h / 2,
        text,
        ha="center",
        va="center",
        fontsize=fontsize,
        wrap=True,
        weight=weight,
    )


def draw_arrow(x1, y1, x2, y2, text=""):
    ax.annotate(
        "",
        xy=(x2, y2),
        xytext=(x1, y1),
        arrowprops=dict(arrowstyle="->", color="black", lw=1.5),
    )
    if text:
        ax.text((x1 + x2) / 2 + 0.2, (y1 + y2) / 2, text, fontsize=9, ha="left")


# Start node
draw_box(4, 8.5, 4, 1, "Multiple Tests?", "#ffcc80", fontsize=11, bold=True)

# First branch - research type
draw_box(
    1.5, 6.5, 3.5, 1, "Confirmatory\n(FWER control)", "#aed581", fontsize=10
)
draw_box(7, 6.5, 3.5, 1, "Exploratory\n(FDR control)", "#81d4fa", fontsize=10)

draw_arrow(5, 8.5, 3.25, 7.5, "Hypothesis-\ndriven")
draw_arrow(7, 8.5, 8.75, 7.5, "Data-\ndriven")

# FWER branches
draw_box(
    0, 4.5, 2.5, 1.2, "Few tests\nor simple\nBonferroni", "#c8e6c9", fontsize=9
)
draw_box(
    3, 4.5, 2.5, 1.2, "Many tests\nor need power\nHolm", "#c8e6c9", fontsize=9
)

draw_arrow(2.5, 6.5, 1.25, 5.7)
draw_arrow(4, 6.5, 4.25, 5.7)

# FDR branches
draw_box(
    6, 4.5, 2.5, 1.2, "Independent\nor positive\nBH", "#b3e5fc", fontsize=9
)
draw_box(9, 4.5, 2.5, 1.2, "Arbitrary\ndependence\nBY", "#b3e5fc", fontsize=9)

draw_arrow(8, 6.5, 7.25, 5.7)
draw_arrow(9.5, 6.5, 10.25, 5.7)

# Post-hoc tests (special case)
draw_box(
    4,
    2,
    4,
    1.5,
    "Post-hoc (after ANOVA):\n• All pairs: Tukey HSD\n• vs Control: Dunnett\n• Complex: Scheffé",
    "#fff59d",
    fontsize=9,
)

ax.set_title(
    "Choosing a Multiple Comparison Correction",
    fontsize=14,
    fontweight="bold",
    y=1.02,
)

plt.tight_layout()
plt.show()
Out[17]:
Visualization
Decision tree diagram for selecting multiple comparison correction methods.
Decision framework for choosing a multiple comparison correction method. The choice depends on whether you're doing confirmatory or exploratory research, the dependence structure among tests, and your tolerance for different types of errors.

Summary

The multiple comparisons problem is one of the most important concepts in modern statistics. When conducting many hypothesis tests, the probability of false positives increases dramatically: from 5% for a single test to 99.4% for 100 tests at α=0.05\alpha = 0.05.

Key concepts:

  • Family-wise error rate (FWER): Probability of at least one false positive; controlled by Bonferroni, Šidák, Holm, Hochberg
  • False discovery rate (FDR): Expected proportion of false positives among rejections; controlled by Benjamini-Hochberg, Benjamini-Yekutieli
  • FWER methods are more conservative, appropriate for confirmatory research
  • FDR methods allow more discoveries, appropriate for exploratory research

Correction methods:

MethodControlsPowerAssumptions
BonferroniFWERLowNone
ŠidákFWERLow-ModerateIndependence
HolmFWERModerateNone
HochbergFWERModerate-HighIndependence/positive dependence
BHFDRHighIndependence/positive dependence
BYFDRModerateNone

For ANOVA post-hoc tests:

  • Tukey HSD for all pairwise comparisons
  • Dunnett for comparisons with control
  • Scheffé for complex contrasts

The dead salmon study reminds us that even absurd results can appear "significant" when we conduct enough tests without correction. Proper handling of multiple comparisons is essential for valid statistical inference.

What's Next

This chapter has covered the multiple comparisons problem and methods for controlling error rates when conducting many tests. You've learned the distinction between FWER and FDR, implemented correction methods from Bonferroni to Benjamini-Hochberg, and explored post-hoc tests for ANOVA.

In the final chapter of this series, we'll bring together all the concepts from hypothesis testing into a comprehensive practical guide. You'll find reference tables, decision frameworks, reporting guidelines, and a complete workflow for conducting hypothesis tests in practice: everything you need to apply these concepts to real data analysis.

Quiz

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about multiple comparisons and false discovery control.

Loading component...

Reference

BIBTEXAcademic
@misc{multiplecomparisonsfwerfdrbonferroniholmbenjaminihochberg, author = {Michael Brenndoerfer}, title = {Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg}, year = {2026}, url = {https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-01-01} }
APAAcademic
Michael Brenndoerfer (2026). Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg. Retrieved from https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg
MLAAcademic
Michael Brenndoerfer. "Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg." 2026. Web. today. <https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg>.
CHICAGOAcademic
Michael Brenndoerfer. "Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg." Accessed today. https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg.
HARVARDAcademic
Michael Brenndoerfer (2026) 'Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg'. Available at: https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg (Accessed: today).
SimpleBasic
Michael Brenndoerfer (2026). Multiple Comparisons: FWER, FDR, Bonferroni, Holm & Benjamini-Hochberg. https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg
Direct link:
https://mbrenndoerfer.com/writing/multiple-comparisons-fwer-fdr-bonferroni-holm-benjamini-hochberg