WritingBooksAboutCommunityContactCommunity

Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation

Michael Brenndoerfer•January 7, 2026•29 min read

Power analysis, sample size determination, MDE calculation, and avoiding underpowered studies. Learn how to design studies with adequate sensitivity to detect meaningful effects.

Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Sample Size, Minimum Detectable Effect, and Power

In 2012, a team of Stanford researchers published a study claiming that organic foods had significant health benefits over conventional foods. The study made headlines worldwide. But critics quickly pointed out a fundamental problem: many of the individual comparisons in the meta-analysis were severely underpowered. Studies with only 10-20 participants were trying to detect subtle differences in nutrient content that would require hundreds of participants to measure reliably. The "no significant difference" conclusions for many nutrients didn't mean organic and conventional foods were the same: they meant the studies simply couldn't tell.

This is one of the most common and costly mistakes in research: conducting a study without first determining whether it has enough statistical power to answer the question being asked. An underpowered study is like trying to hear a whisper at a rock concert: even if the signal exists, you'll never detect it through the noise.

Power analysis is the process of determining how many observations you need to detect effects of a given size with a specified probability. It's arguably the most important practical skill in hypothesis testing, because even the most elegant experimental design is worthless if the sample size is too small to detect the effects you care about.

This section builds directly on the concepts of Type I and Type II errors. You learned that β is the probability of missing a true effect, and power (1 - β) is the probability of detecting it. Now you'll learn how to calculate the sample size needed to achieve a desired power level for effects of a given magnitude.

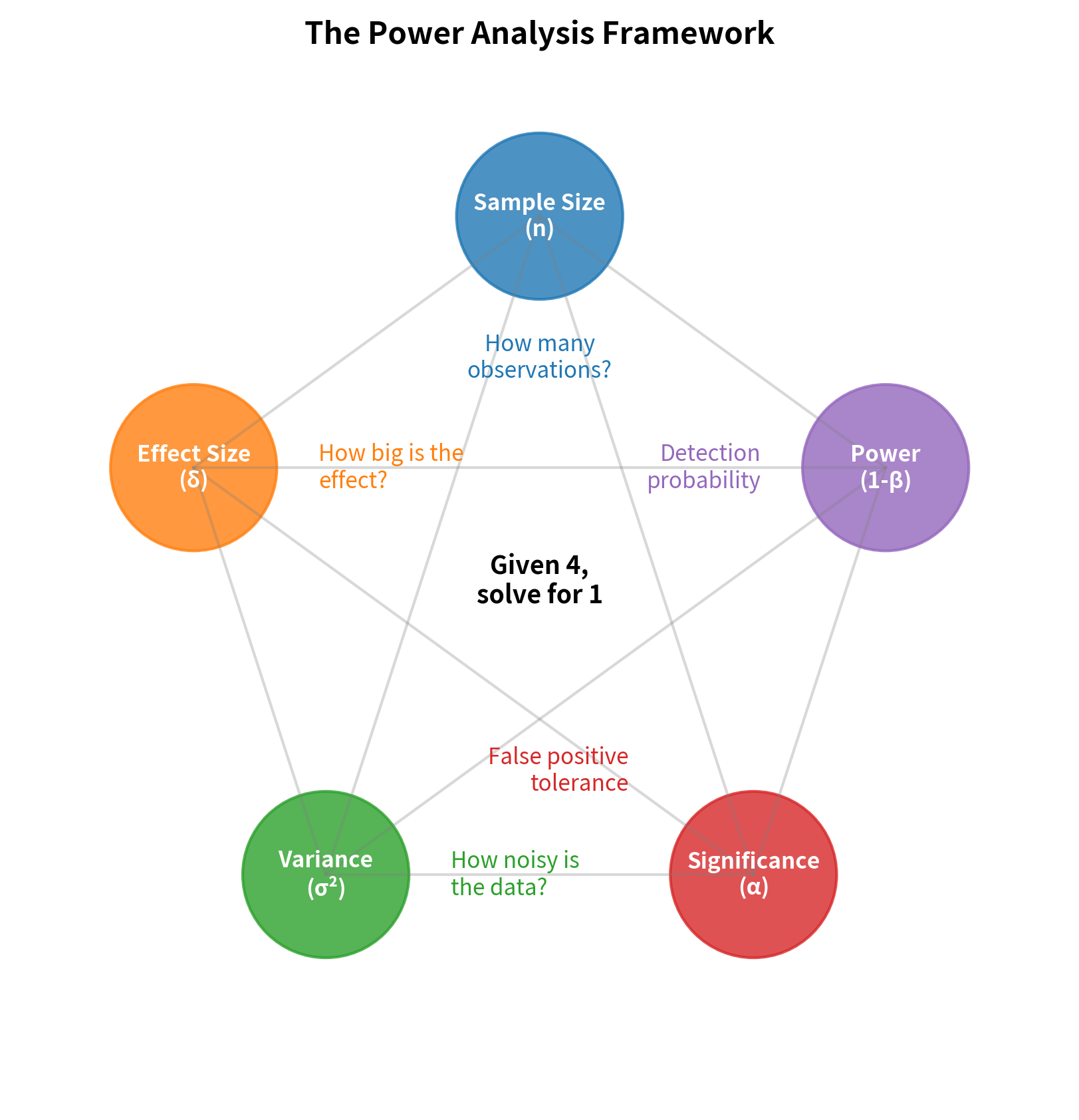
The Power Analysis Framework

Power analysis connects five interrelated quantities. Given any four, you can solve for the fifth:

Out[2]:
Visualization
Pentagon diagram showing the five interconnected quantities in power analysis.
The five quantities in power analysis are interconnected. Given any four, you can calculate the fifth. The most common use case is solving for sample size (n) given the other four quantities, but you might also solve for minimum detectable effect given a fixed budget, or for power given a fixed sample size.

The Five Quantities

1. Sample Size (n): The number of observations in your study. Larger samples provide more information and reduce uncertainty.

2. Effect Size (δ): The magnitude of the true effect you're trying to detect. This can be expressed in raw units (e.g., "10 mmHg reduction in blood pressure") or standardized units (e.g., Cohen's d = 0.5).

3. Population Variance (σ²): The natural variability in your measurements. More variance means more noise, making signals harder to detect.

4. Significance Level (α): The probability of Type I error you're willing to accept. Lower α means more stringent requirements for rejecting the null hypothesis.

5. Power (1 - β): The probability of correctly detecting a true effect. Higher power means greater sensitivity to real effects.

The Relationships

These quantities are connected by fundamental relationships that govern all hypothesis tests:

  • Larger sample sizes increase power because more data reduces sampling variability
  • Larger effect sizes increase power because bigger signals are easier to detect
  • Higher variance decreases power because more noise obscures the signal
  • Lower α decreases power because stricter criteria make rejection harder
  • Targeting higher power requires larger samples to achieve greater sensitivity

Deriving the Sample Size Formula

Let's derive the sample size formula for the most common case: a one-sample z-test. The same logic extends to other tests with minor modifications.

Setup

We want to test:

  • H0:μ=μ0H_0: \mu = \mu_0 (null hypothesis)
  • H1:μ=μ1H_1: \mu = \mu_1 (specific alternative, where μ1=μ0+δ\mu_1 = \mu_0 + \delta)

With:

  • Known population standard deviation σ
  • Significance level α (two-tailed)
  • Desired power 1 - β

The Derivation

Step 1: Find the rejection criterion under H₀

Under the null hypothesis, the test statistic Z=Xˉ−μ0σ/nZ = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} follows N(0, 1).

We reject H0H_0 when ∣Z∣>zα/2|Z| > z_{\alpha/2}, which corresponds to:

Xˉ>μ0+zα/2⋅σnorXˉ<μ0−zα/2⋅σn\bar{X} > \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} \quad \text{or} \quad \bar{X} < \mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}

Step 2: Calculate power under H₁

Under the alternative H1:μ=μ1H_1: \mu = \mu_1, we want:

Power=P(Reject H0∣H1 true)=1−β\text{Power} = P(\text{Reject } H_0 \mid H_1 \text{ true}) = 1 - \beta

For a one-sided test (detecting μ1>μ0\mu_1 > \mu_0), the power is:

Power=P(Xˉ>μ0+zα/2⋅σn∣μ=μ1)\text{Power} = P\left(\bar{X} > \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} \mid \mu = \mu_1\right)

Under H1H_1, Xˉ∼N(μ1,σ2/n)\bar{X} \sim N(\mu_1, \sigma^2/n). Standardizing:

Power=P(Z>μ0+zα/2⋅σn−μ1σ/n)\text{Power} = P\left(Z > \frac{\mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} - \mu_1}{\sigma/\sqrt{n}}\right) =P(Z>zα/2−μ1−μ0σ/n)= P\left(Z > z_{\alpha/2} - \frac{\mu_1 - \mu_0}{\sigma/\sqrt{n}}\right) =P(Z>zα/2−δnσ)= P\left(Z > z_{\alpha/2} - \frac{\delta \sqrt{n}}{\sigma}\right)

Step 3: Solve for n

Setting power equal to 1−β1 - \beta:

1−β=P(Z>zα/2−δnσ)1 - \beta = P\left(Z > z_{\alpha/2} - \frac{\delta \sqrt{n}}{\sigma}\right)

This means:

zα/2−δnσ=−z1−β=−zβz_{\alpha/2} - \frac{\delta \sqrt{n}}{\sigma} = -z_{1-\beta} = -z_\beta

Note: z1−βz_{1-\beta} is the z-value such that P(Z>z1−β)=βP(Z > z_{1-\beta}) = \beta, so P(Z<z1−β)=1−βP(Z < z_{1-\beta}) = 1 - \beta.

Solving for n:

δnσ=zα/2+z1−β\frac{\delta \sqrt{n}}{\sigma} = z_{\alpha/2} + z_{1-\beta} n=(zα/2+z1−β)σδ\sqrt{n} = \frac{(z_{\alpha/2} + z_{1-\beta}) \sigma}{\delta} n=(zα/2+z1−βδ/σ)2=(zα/2+z1−βd)2\boxed{n = \left(\frac{z_{\alpha/2} + z_{1-\beta}}{\delta/\sigma}\right)^2 = \left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2}

where d=δ/σd = \delta/\sigma is the standardized effect size (Cohen's d).

In[3]:
Code
import numpy as np
from scipy import stats


def sample_size_one_sample(effect_size, sigma=1, alpha=0.05, power=0.80):
    """
    Calculate required sample size for a one-sample z-test.

    Parameters:
    -----------
    effect_size : float
        The minimum detectable effect in original units
    sigma : float
        Population standard deviation
    alpha : float
        Significance level (two-tailed)
    power : float
        Desired power (1 - beta)

    Returns:
    --------
    int : Required sample size (rounded up)
    """
    # Standardized effect size (Cohen's d)
    d = effect_size / sigma

    # Critical values
    z_alpha = stats.norm.ppf(1 - alpha / 2)  # Two-tailed
    z_beta = stats.norm.ppf(power)  # Power quantile

    # Sample size formula
    n = ((z_alpha + z_beta) / d) ** 2

    return int(np.ceil(n))


# Example: Detect a medium effect (d = 0.5) with 80% power at α = 0.05
n = sample_size_one_sample(effect_size=0.5, sigma=1, alpha=0.05, power=0.80)
print("One-sample z-test for d = 0.5:")
print(f"  Required n = {n}")

# Verify the components
z_alpha = stats.norm.ppf(0.975)
z_beta = stats.norm.ppf(0.80)
print("\nComponents:")
print(f"  z_α/2 = {z_alpha:.4f}")
print(f"  z_(1-β) = {z_beta:.4f}")
print(f"  Sum = {z_alpha + z_beta:.4f}")
print(
    f"  n = ({z_alpha + z_beta:.4f} / 0.5)² = {((z_alpha + z_beta) / 0.5) ** 2:.1f}"
)
Out[3]:
Console
One-sample z-test for d = 0.5:
  Required n = 32

Components:
  z_α/2 = 1.9600
  z_(1-β) = 0.8416
  Sum = 2.8016
  n = (2.8016 / 0.5)² = 31.4

Sample Size Formulas for Common Tests

Different tests require slightly different formulas. Here are the most common ones:

Two-Sample t-test (Equal Variances)

For comparing two independent groups with nn observations each:

n=2(zα/2+z1−βd)2n = 2 \left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2

The factor of 2 accounts for the increased variance when comparing two groups.

In[4]:
Code
def sample_size_two_sample(effect_size, sigma=1, alpha=0.05, power=0.80):
    """
    Calculate required sample size per group for a two-sample t-test.

    Parameters:
    -----------
    effect_size : float
        The minimum detectable difference between groups
    sigma : float
        Common standard deviation (assumed equal in both groups)
    alpha : float
        Significance level (two-tailed)
    power : float
        Desired power

    Returns:
    --------
    int : Required sample size per group (rounded up)
    """
    d = effect_size / sigma
    z_alpha = stats.norm.ppf(1 - alpha / 2)
    z_beta = stats.norm.ppf(power)

    # Factor of 2 for two-sample test
    n = 2 * ((z_alpha + z_beta) / d) ** 2

    return int(np.ceil(n))


# Example: Two-sample test for medium effect
n_per_group = sample_size_two_sample(
    effect_size=0.5, sigma=1, alpha=0.05, power=0.80
)
print("Two-sample t-test for d = 0.5:")
print(f"  Required n per group = {n_per_group}")
print(f"  Total N = {2 * n_per_group}")
Out[4]:
Console
Two-sample t-test for d = 0.5:
  Required n per group = 63
  Total N = 126

Paired t-test

For paired observations (before/after, matched pairs):

n=(zα/2+z1−βd)2n = \left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2

where d=δ/σdd = \delta / \sigma_d and σd\sigma_d is the standard deviation of the differences.

The paired design is typically more efficient because it removes between-subject variability.

In[5]:
Code
def sample_size_paired(effect_size, sigma_diff, alpha=0.05, power=0.80):
    """
    Calculate required number of pairs for a paired t-test.

    Parameters:
    -----------
    effect_size : float
        The minimum detectable mean difference
    sigma_diff : float
        Standard deviation of the paired differences
    alpha : float
        Significance level (two-tailed)
    power : float
        Desired power

    Returns:
    --------
    int : Required number of pairs (rounded up)
    """
    d = effect_size / sigma_diff
    z_alpha = stats.norm.ppf(1 - alpha / 2)
    z_beta = stats.norm.ppf(power)

    n = ((z_alpha + z_beta) / d) ** 2

    return int(np.ceil(n))


# Example: Paired test - before/after study
# Expect 5-point improvement, SD of differences = 10
n_pairs = sample_size_paired(
    effect_size=5, sigma_diff=10, alpha=0.05, power=0.80
)
print("Paired t-test (effect=5, SD_diff=10):")
print(f"  Required n pairs = {n_pairs}")
Out[5]:
Console
Paired t-test (effect=5, SD_diff=10):
  Required n pairs = 32

Test for Two Proportions

For comparing two proportions p1p_1 and p2p_2:

n=(zα/22pˉ(1−pˉ)+z1−βp1(1−p1)+p2(1−p2)p1−p2)2n = \left(\frac{z_{\alpha/2}\sqrt{2\bar{p}(1-\bar{p})} + z_{1-\beta}\sqrt{p_1(1-p_1) + p_2(1-p_2)}}{p_1 - p_2}\right)^2

where pˉ=(p1+p2)/2\bar{p} = (p_1 + p_2)/2.

In[6]:
Code
def sample_size_proportions(p1, p2, alpha=0.05, power=0.80):
    """
    Calculate required sample size per group for comparing two proportions.

    Parameters:
    -----------
    p1 : float
        Expected proportion in group 1 (e.g., control)
    p2 : float
        Expected proportion in group 2 (e.g., treatment)
    alpha : float
        Significance level (two-tailed)
    power : float
        Desired power

    Returns:
    --------
    int : Required sample size per group (rounded up)
    """
    z_alpha = stats.norm.ppf(1 - alpha / 2)
    z_beta = stats.norm.ppf(power)

    # Pooled proportion
    p_bar = (p1 + p2) / 2

    # Formula components
    numerator = z_alpha * np.sqrt(2 * p_bar * (1 - p_bar)) + z_beta * np.sqrt(
        p1 * (1 - p1) + p2 * (1 - p2)
    )
    denominator = abs(p1 - p2)

    n = (numerator / denominator) ** 2

    return int(np.ceil(n))


# Example: A/B test - detect 5% improvement from 10% to 15% conversion
n_per_group = sample_size_proportions(p1=0.10, p2=0.15, alpha=0.05, power=0.80)
print("Two-proportion test (10% vs 15%):")
print(f"  Required n per group = {n_per_group}")
print(f"  Total N = {2 * n_per_group}")
Out[6]:
Console
Two-proportion test (10% vs 15%):
  Required n per group = 686
  Total N = 1372

Summary Table

Test TypeSample Size FormulaNotes
One-sample z/tn=(zα/2+z1−βd)2n = \left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2d = δ/σ
Two-sample tn=2(zα/2+z1−βd)2n = 2\left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2n per group
Paired tn=(zα/2+z1−βd)2n = \left(\frac{z_{\alpha/2} + z_{1-\beta}}{d}\right)^2n pairs, d = δ/σ_d
Two proportionsComplex formula aboven per group

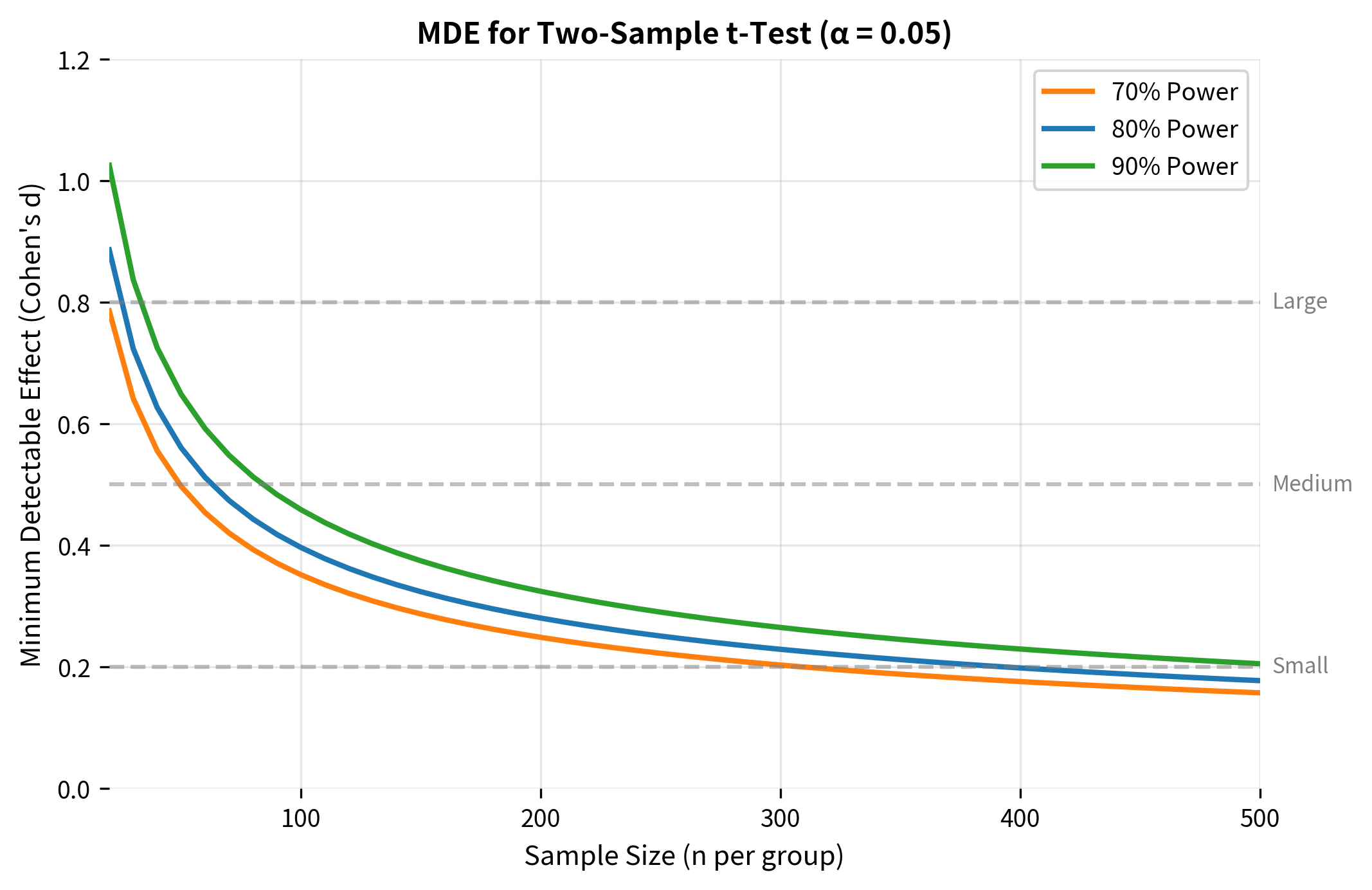
Minimum Detectable Effect (MDE)

Sometimes you have a fixed sample size (due to budget, time, or available participants) and need to know: What's the smallest effect this study can reliably detect?

The minimum detectable effect (MDE) answers this question. It's the effect size threshold below which your study has inadequate power.

Deriving the MDE Formula

Rearranging the sample size formula to solve for effect size:

d=zα/2+z1−βnd = \frac{z_{\alpha/2} + z_{1-\beta}}{\sqrt{n}}

For a two-sample test:

d=zα/2+z1−βn/2d = \frac{z_{\alpha/2} + z_{1-\beta}}{\sqrt{n/2}}
In[7]:
Code
def minimum_detectable_effect(
    n, alpha=0.05, power=0.80, test_type="one_sample"
):
    """
    Calculate the minimum detectable effect size (Cohen's d).

    Parameters:
    -----------
    n : int
        Sample size (total for one-sample, per group for two-sample)
    alpha : float
        Significance level (two-tailed)
    power : float
        Desired power
    test_type : str
        'one_sample' or 'two_sample'

    Returns:
    --------
    float : Minimum detectable Cohen's d
    """
    z_alpha = stats.norm.ppf(1 - alpha / 2)
    z_beta = stats.norm.ppf(power)

    if test_type == "two_sample":
        mde = (z_alpha + z_beta) / np.sqrt(n / 2)
    else:
        mde = (z_alpha + z_beta) / np.sqrt(n)

    return mde


# Example: What can we detect with n = 50?
print("Minimum Detectable Effect (Cohen's d) with 80% power, α = 0.05:\n")
for n in [20, 50, 100, 200, 500]:
    mde_one = minimum_detectable_effect(n, test_type="one_sample")
    mde_two = minimum_detectable_effect(n, test_type="two_sample")
    print(
        f"n = {n:3d}: One-sample d = {mde_one:.3f}, Two-sample d = {mde_two:.3f}"
    )
Out[7]:
Console
Minimum Detectable Effect (Cohen's d) with 80% power, α = 0.05:

n =  20: One-sample d = 0.626, Two-sample d = 0.886
n =  50: One-sample d = 0.396, Two-sample d = 0.560
n = 100: One-sample d = 0.280, Two-sample d = 0.396
n = 200: One-sample d = 0.198, Two-sample d = 0.280
n = 500: One-sample d = 0.125, Two-sample d = 0.177
Out[8]:
Visualization
Line plot showing MDE decreasing with sample size for different power levels.
Minimum detectable effect (MDE) as a function of sample size for different power levels. The curves show how larger samples allow detection of smaller effects. At 80% power, a two-sample study with n = 100 per group can detect effects of d ≈ 0.40. The dashed lines mark conventional effect size benchmarks (small = 0.2, medium = 0.5, large = 0.8).

MDE in Practice: A/B Testing

MDE is particularly important for A/B testing in tech companies. Before running an experiment, you need to know:

  1. What's the smallest improvement worth detecting?
  2. How much traffic/time do we need to detect it?
In[9]:
Code
def ab_test_mde_proportions(n_per_group, baseline_rate, alpha=0.05, power=0.80):
    """
    Calculate MDE for an A/B test on proportions (e.g., conversion rate).

    Parameters:
    -----------
    n_per_group : int
        Sample size per group
    baseline_rate : float
        Expected conversion rate in control group
    alpha : float
        Significance level
    power : float
        Desired power

    Returns:
    --------
    tuple : (absolute MDE, relative MDE as percentage lift)
    """
    z_alpha = stats.norm.ppf(1 - alpha / 2)
    z_beta = stats.norm.ppf(power)

    # Standard error under null (pooled)
    se_null = np.sqrt(2 * baseline_rate * (1 - baseline_rate) / n_per_group)

    # Standard error under alternative (approximate)
    se_alt = se_null  # Approximation for small effects

    # MDE (absolute)
    mde_abs = (z_alpha + z_beta) * se_null

    # Relative lift
    mde_relative = mde_abs / baseline_rate * 100

    return mde_abs, mde_relative


# Example: E-commerce A/B test
baseline = 0.03  # 3% conversion rate
print(f"A/B Test MDE Analysis (baseline rate = {baseline * 100}%)\n")
print(f"{'n per group':<15} {'MDE (absolute)':<18} {'MDE (% lift)':<15}")
print("-" * 48)

for n in [1000, 5000, 10000, 50000, 100000]:
    mde_abs, mde_rel = ab_test_mde_proportions(n, baseline)
    print(f"{n:<15,} {mde_abs:<18.4f} {mde_rel:<15.1f}%")
Out[9]:
Console
A/B Test MDE Analysis (baseline rate = 3.0%)

n per group     MDE (absolute)     MDE (% lift)   
------------------------------------------------
1,000           0.0214             71.2           %
5,000           0.0096             31.9           %
10,000          0.0068             22.5           %
50,000          0.0030             10.1           %
100,000         0.0021             7.1            %

This analysis reveals an important truth: detecting small improvements in conversion rates requires very large samples. A 10% relative lift on a 3% baseline means detecting a 0.3 percentage point improvement, which requires roughly 35,000 users per group.

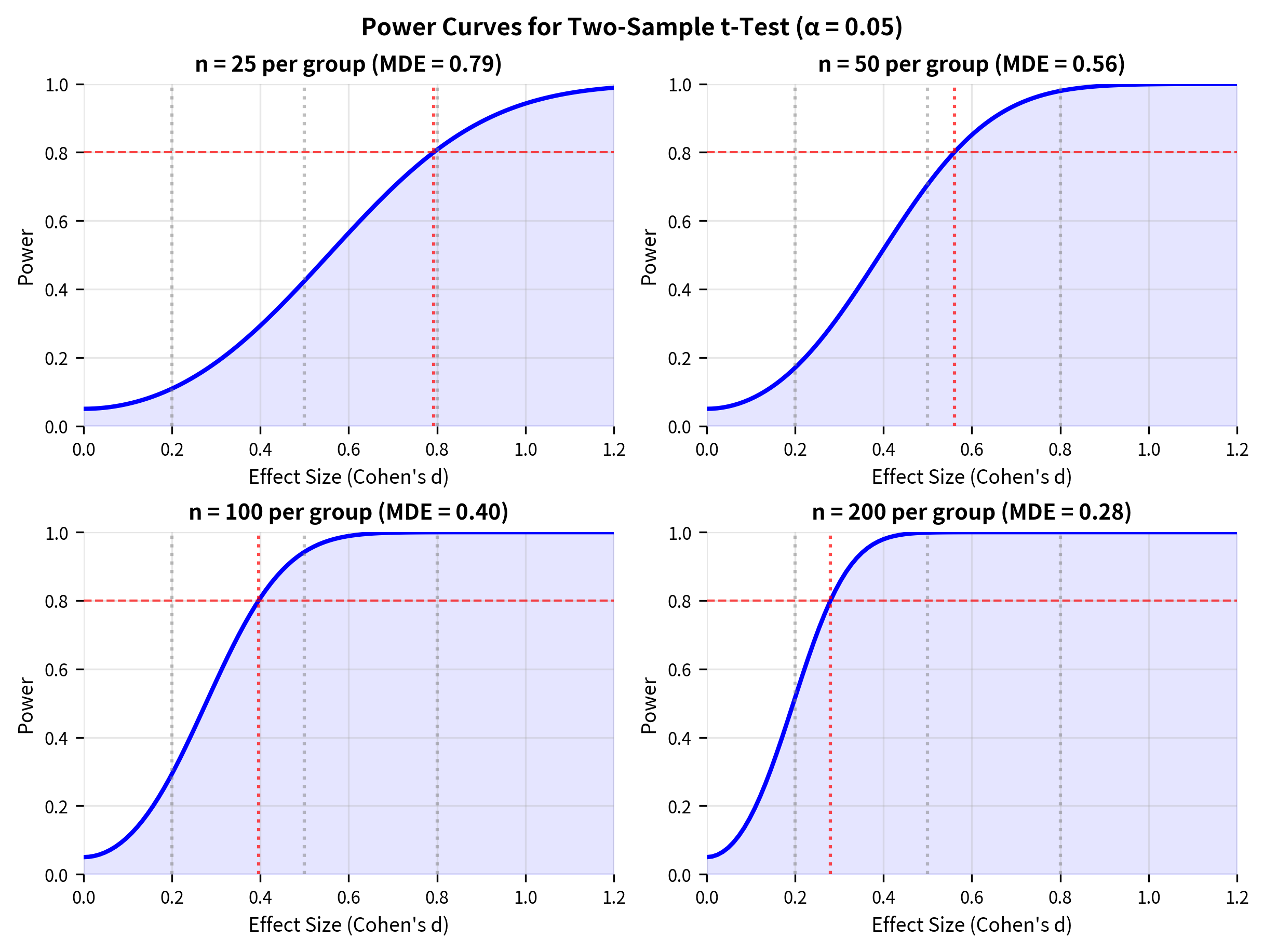
Visualizing Power Analysis

Understanding how the five quantities interact is easier with visualization.

Out[10]:
Visualization
Heatmap showing required sample size for different effect sizes and power levels.
Required sample size as a function of effect size and power. Smaller effect sizes and higher power requirements demand dramatically larger samples. The white contour lines show specific sample size thresholds. Note how requirements escalate rapidly when trying to detect small effects (d < 0.3) with high power.
Out[11]:
Visualization
Four panel plot showing power curves for different sample sizes.
Sensitivity analysis showing how achieved power depends on sample size and effect size. Each subplot shows the power curve for a different sample size. Larger samples shift the power curves leftward, allowing detection of smaller effects. The horizontal dashed line marks 80% power. The vertical dashed lines mark conventional effect size benchmarks.

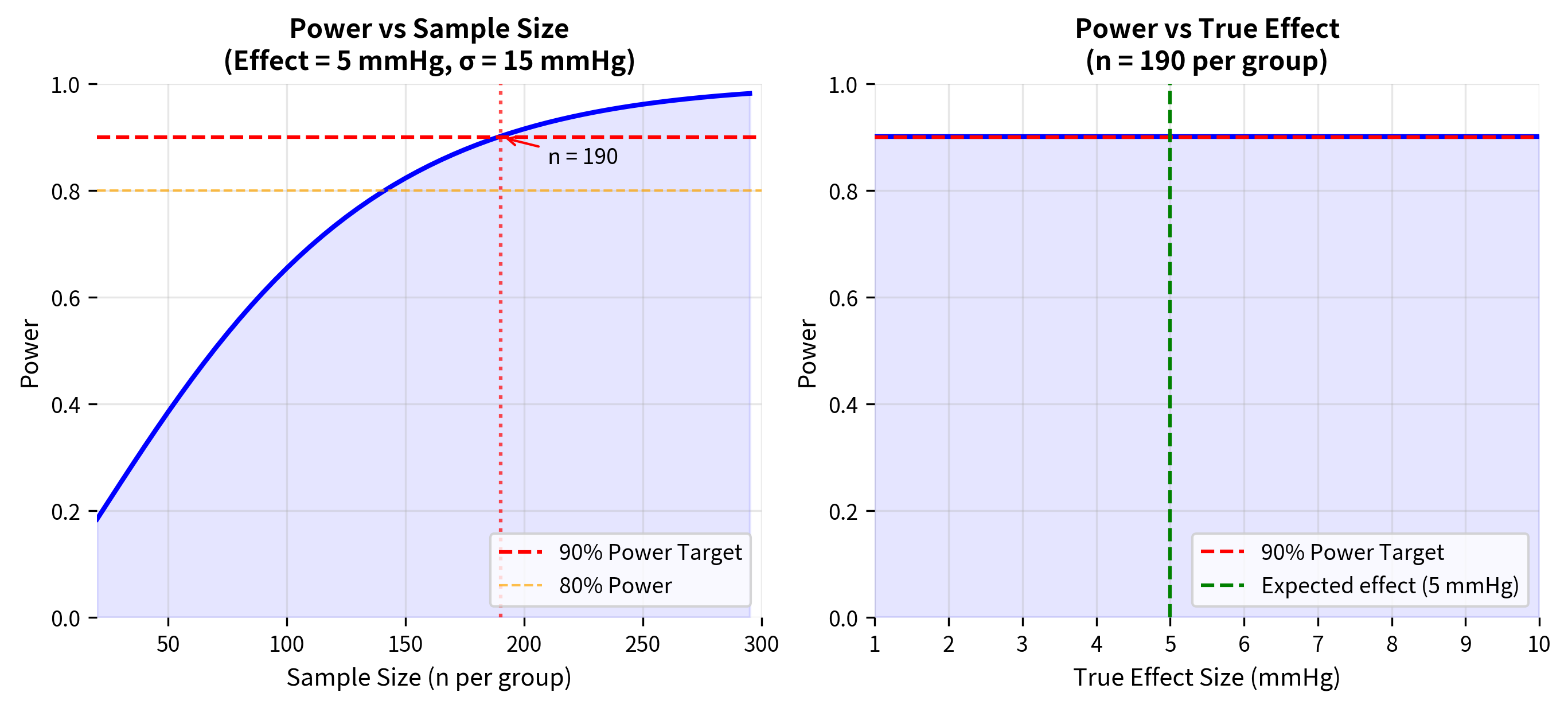
Worked Example: Clinical Trial Design

Let's work through a complete power analysis for a realistic scenario.

Scenario: A pharmaceutical company is designing a clinical trial to test whether a new blood pressure medication reduces systolic blood pressure more than the current standard treatment. Based on pilot data:

  • Current treatment reduces systolic BP by 10 mmHg on average
  • Standard deviation of BP reduction is approximately 15 mmHg
  • The company wants to detect a 5 mmHg additional reduction (clinically meaningful)
  • They want 90% power to ensure reliable results
  • Using standard α = 0.05 (two-tailed)
In[12]:
Code
import numpy as np
from scipy import stats

# Study parameters
current_treatment_effect = 10  # mmHg reduction
new_treatment_effect = 15  # Expected mmHg reduction
effect_size = new_treatment_effect - current_treatment_effect  # 5 mmHg
sigma = 15  # Standard deviation
alpha = 0.05
target_power = 0.90

print("=== Clinical Trial Power Analysis ===\n")
print("Parameters:")
print(f"  Expected effect: {effect_size} mmHg improvement over standard")
print(f"  Standard deviation: {sigma} mmHg")
print(f"  Significance level: α = {alpha}")
print(f"  Target power: {target_power * 100}%")

# Calculate Cohen's d
d = effect_size / sigma
print(f"\nStandardized effect size (Cohen's d): {d:.3f}")

# Sample size calculation
z_alpha = stats.norm.ppf(1 - alpha / 2)
z_beta = stats.norm.ppf(target_power)

n_per_group = 2 * ((z_alpha + z_beta) / d) ** 2
n_per_group = int(np.ceil(n_per_group))

print("\n=== Required Sample Size ===")
print(f"  z_α/2 = {z_alpha:.4f}")
print(f"  z_(1-β) = {z_beta:.4f}")
print(f"  n per group = 2 × (({z_alpha:.3f} + {z_beta:.3f}) / {d:.3f})²")
print(f"  n per group = {n_per_group}")
print(f"  Total participants = {2 * n_per_group}")
Out[12]:
Console
=== Clinical Trial Power Analysis ===

Parameters:
  Expected effect: 5 mmHg improvement over standard
  Standard deviation: 15 mmHg
  Significance level: α = 0.05
  Target power: 90.0%

Standardized effect size (Cohen's d): 0.333

=== Required Sample Size ===
  z_α/2 = 1.9600
  z_(1-β) = 1.2816
  n per group = 2 × ((1.960 + 1.282) / 0.333)²
  n per group = 190
  Total participants = 380
In[13]:
Code
# Sensitivity analysis: What if our assumptions are wrong?

print("\n=== Sensitivity Analysis ===\n")
print("What if the true effect or variability differs from our assumptions?\n")

# Vary effect size
print("1. Effect Size Sensitivity (σ = 15 mmHg, power = 90%):")
print(f"   {'Effect (mmHg)':<15} {'Cohen d':<10} {'n per group':<15}")
print("   " + "-" * 40)
for effect in [3, 4, 5, 6, 7]:
    d = effect / sigma
    n = 2 * ((z_alpha + z_beta) / d) ** 2
    print(f"   {effect:<15} {d:<10.3f} {int(np.ceil(n)):<15}")

# Vary standard deviation
print("\n2. Variance Sensitivity (effect = 5 mmHg, power = 90%):")
print(f"   {'SD (mmHg)':<15} {'Cohen d':<10} {'n per group':<15}")
print("   " + "-" * 40)
for sd in [10, 12, 15, 18, 20]:
    d = effect_size / sd
    n = 2 * ((z_alpha + z_beta) / d) ** 2
    print(f"   {sd:<15} {d:<10.3f} {int(np.ceil(n)):<15}")

# Vary power
print("\n3. Power Sensitivity (effect = 5 mmHg, σ = 15 mmHg):")
print(f"   {'Power':<15} {'n per group':<15} {'Total N':<15}")
print("   " + "-" * 45)
for power in [0.70, 0.80, 0.85, 0.90, 0.95]:
    z_b = stats.norm.ppf(power)
    n = 2 * ((z_alpha + z_b) / d) ** 2
    n = int(np.ceil(n))
    print(f"   {power * 100:.0f}%{'':<10} {n:<15} {2 * n:<15}")
Out[13]:
Console

=== Sensitivity Analysis ===

What if the true effect or variability differs from our assumptions?

1. Effect Size Sensitivity (σ = 15 mmHg, power = 90%):
   Effect (mmHg)   Cohen d    n per group    
   ----------------------------------------
   3               0.200      526            
   4               0.267      296            
   5               0.333      190            
   6               0.400      132            
   7               0.467      97             

2. Variance Sensitivity (effect = 5 mmHg, power = 90%):
   SD (mmHg)       Cohen d    n per group    
   ----------------------------------------
   10              0.500      85             
   12              0.417      122            
   15              0.333      190            
   18              0.278      273            
   20              0.250      337            

3. Power Sensitivity (effect = 5 mmHg, σ = 15 mmHg):
   Power           n per group     Total N        
   ---------------------------------------------
   70%           198             396            
   80%           252             504            
   85%           288             576            
   90%           337             674            
   95%           416             832
Out[14]:
Visualization
Two panel figure showing power curves for the clinical trial example.
Power analysis for the blood pressure clinical trial. Left: Power as a function of sample size, showing the 90% target. Right: Power as a function of true effect size, given the planned sample of 190 per group. The shaded regions indicate the parameter space where the study achieves adequate power.

Decision Summary

In[15]:
Code
print("=== Clinical Trial Design Decision ===\n")

n_required = 190  # From our calculation
dropout_rate = 0.15  # Typical for clinical trials
n_enrolled = int(np.ceil(n_required / (1 - dropout_rate)))

print("Recommended Design:")
print(f"  • Enroll {n_enrolled} patients per group ({2 * n_enrolled} total)")
print(f"    (Accounts for {dropout_rate * 100:.0f}% expected dropout)")
print(f"  • Expected completers: {n_required} per group")
print("  • Power: 90% to detect 5 mmHg difference")
print("  • MDE at enrolled sample: ~4.3 mmHg")
print()
print("Study Characteristics:")
print("  • Can detect effects as small as Cohen's d = 0.29")
print("  • 10% risk of missing a true 5 mmHg effect (Type II)")
print("  • 5% risk of false positive (Type I)")
print()
print("Practical Considerations:")
print("  • Budget for ~450 total enrolled patients")
print("  • Allow for longer recruitment if dropout > expected")
print("  • Consider adaptive design if early results warrant")
Out[15]:
Console
=== Clinical Trial Design Decision ===

Recommended Design:
  • Enroll 224 patients per group (448 total)
    (Accounts for 15% expected dropout)
  • Expected completers: 190 per group
  • Power: 90% to detect 5 mmHg difference
  • MDE at enrolled sample: ~4.3 mmHg

Study Characteristics:
  • Can detect effects as small as Cohen's d = 0.29
  • 10% risk of missing a true 5 mmHg effect (Type II)
  • 5% risk of false positive (Type I)

Practical Considerations:
  • Budget for ~450 total enrolled patients
  • Allow for longer recruitment if dropout > expected
  • Consider adaptive design if early results warrant

The Problem of Underpowered Studies

Underpowered studies are one of the most pervasive problems in research. When a study has insufficient power:

Consequences of Low Power

1. High False Negative Rate: Real effects are missed because the study lacks sensitivity to detect them. This wastes resources and may lead to abandoning potentially useful treatments or interventions.

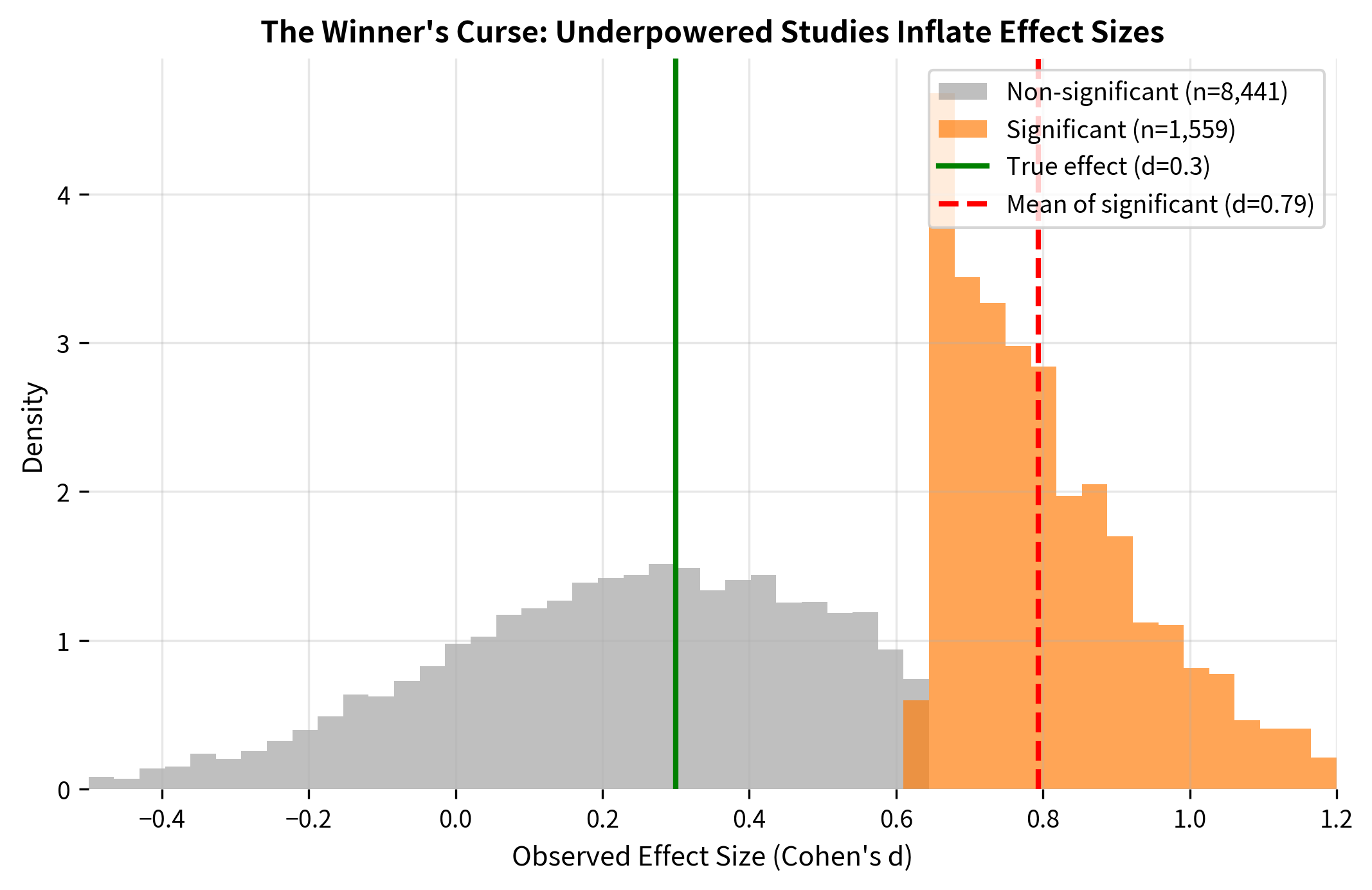
2. Winner's Curse (Effect Size Inflation): When an underpowered study does achieve significance, the estimated effect size is systematically inflated. Only the "lucky" samples with upward random fluctuations cross the significance threshold.

In[16]:
Code
import numpy as np
from scipy import stats

np.random.seed(42)

# Simulate many underpowered studies
true_effect = 0.3  # Small true effect (Cohen's d)
n_per_group = 20  # Small sample (underpowered for this effect)
n_simulations = 10000

significant_effects = []
all_effects = []

for _ in range(n_simulations):
    # Generate data
    group1 = np.random.normal(0, 1, n_per_group)
    group2 = np.random.normal(true_effect, 1, n_per_group)

    # Calculate observed effect
    pooled_std = np.sqrt((np.var(group1, ddof=1) + np.var(group2, ddof=1)) / 2)
    observed_d = (np.mean(group2) - np.mean(group1)) / pooled_std
    all_effects.append(observed_d)

    # Test significance
    _, p = stats.ttest_ind(group2, group1)
    if p < 0.05:
        significant_effects.append(observed_d)

power = len(significant_effects) / n_simulations
mean_significant = np.mean(significant_effects) if significant_effects else 0
inflation = (mean_significant / true_effect - 1) * 100

print("=== Winner's Curse Simulation ===\n")
print(f"True effect size: d = {true_effect}")
print(f"Sample size: n = {n_per_group} per group (underpowered)")
print(f"Simulated power: {power:.1%}")
print()
print(f"Among {len(significant_effects):,} significant results:")
print(f"  Mean observed effect: d = {mean_significant:.3f}")
print(f"  True effect: d = {true_effect:.3f}")
print(f"  Inflation: {inflation:.0f}%")
Out[16]:
Console
=== Winner's Curse Simulation ===

True effect size: d = 0.3
Sample size: n = 20 per group (underpowered)
Simulated power: 15.6%

Among 1,559 significant results:
  Mean observed effect: d = 0.793
  True effect: d = 0.300
  Inflation: 164%
Out[17]:
Visualization
Histogram showing effect size distribution with significant results highlighted.
The Winner''s Curse: effect size estimates from underpowered studies. The histogram shows the distribution of observed effect sizes across 10,000 simulated studies. The true effect is d = 0.3 (vertical green line). Studies that achieve significance (orange) have systematically inflated effect estimates because only samples with large random fluctuations cross the threshold.

3. Non-Replicability: Inflated effect sizes from underpowered studies are unlikely to replicate. Follow-up studies with the same sample size will often fail to reach significance, contributing to the "replication crisis."

4. Wasted Resources: Underpowered studies waste time, money, and participant effort on research that cannot reliably answer the question being asked.

Avoiding Underpowered Studies

The solution is straightforward: conduct power analysis before data collection. This involves:

  1. Specify the smallest effect size of practical importance: What's the minimum effect worth detecting? This is a scientific/business question, not a statistical one.

  2. Choose target power: The convention is 80%, but 90% is better for confirmatory research.

  3. Calculate required sample size: Use the formulas and tools covered in this section.

  4. If required sample is infeasible: Either accept lower power (with documented limitations), seek more funding/participants, or consider whether the study should be conducted at all.

An underpowered study with uncertain results is often worse than no study at all, because it can mislead future research and policy decisions.

Practical Power Analysis Tools

While understanding the formulas is important, in practice you'll often use software tools.

Python: statsmodels

In[18]:
Code
from statsmodels.stats.power import TTestIndPower

# Two-sample t-test power analysis
analysis = TTestIndPower()

# Calculate required sample size
n = analysis.solve_power(
    effect_size=0.5,  # Cohen's d
    alpha=0.05,
    power=0.80,
    alternative="two-sided",
)
print("Two-sample t-test (d=0.5, power=80%, α=0.05):")
print(f"  Required n per group: {np.ceil(n):.0f}")

# Calculate power for given n
power = analysis.solve_power(
    effect_size=0.5,
    nobs1=64,  # n per group
    alpha=0.05,
    alternative="two-sided",
)
print("\nWith n=64 per group:")
print(f"  Achieved power: {power:.1%}")

# Calculate MDE for given n and power
mde = analysis.solve_power(
    nobs1=100, alpha=0.05, power=0.80, alternative="two-sided"
)
print("\nWith n=100 per group, 80% power:")
print(f"  Minimum detectable effect: d = {mde:.3f}")
Out[18]:
Console
Two-sample t-test (d=0.5, power=80%, α=0.05):
  Required n per group: 64

With n=64 per group:
  Achieved power: 80.1%

With n=100 per group, 80% power:
  Minimum detectable effect: d = 0.398

Power Analysis Checklist

When planning a study, work through this checklist:

  1. Define the hypothesis clearly: What exactly are you testing?

  2. Determine the appropriate test: One-sample, two-sample, paired, proportions, etc.

  3. Specify the minimum effect size of interest: Based on practical significance, not statistical convenience.

  4. Estimate population variance: From pilot data, literature, or conservative assumptions.

  5. Choose significance level: Usually α = 0.05, but consider context.

  6. Set target power: At least 80%, preferably 90% for confirmatory research.

  7. Calculate required sample size: Using appropriate formulas or software.

  8. Conduct sensitivity analysis: What if assumptions are wrong?

  9. Document all assumptions: For transparency and reproducibility.

  10. Assess feasibility: Is the required sample achievable?

Summary

Power analysis is essential for designing studies that can actually answer research questions. The key points are:

The five quantities (sample size, effect size, variance, α, power) are mathematically connected. Given any four, you can solve for the fifth.

Sample size formulas vary by test type but share a common structure. The key insight is that requirements scale with the square of the ratio (z_α + z_β)/d, so small changes in effect size dramatically affect sample needs.

Minimum detectable effect (MDE) tells you the smallest effect your study can reliably detect. This is crucial for assessing whether a study is worth conducting.

Underpowered studies have serious consequences: high false negative rates, inflated effect estimates (winner's curse), and poor replicability.

Power analysis should be done before data collection, not after. Post-hoc power analysis is meaningless because it's just a transformation of the p-value.

Sensitivity analysis is important because effect size and variance assumptions are often uncertain. Understand how your conclusions change if assumptions are wrong.

What's Next

With sample size determination mastered, you're ready to explore effect sizes in depth. Effect sizes quantify the magnitude of effects in standardized units, making them comparable across studies and contexts. You'll learn:

  • Why statistical significance is not the same as practical significance
  • How to calculate and interpret various effect size measures
  • The relationship between effect size, sample size, and significance
  • How to report effect sizes alongside p-values for complete statistical reporting

After effect sizes, you'll learn about multiple comparisons: what happens to power and error rates when you conduct many tests simultaneously. The final section ties all these concepts together with practical guidelines for statistical analysis and reporting.

Quiz

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about sample size, minimum detectable effect, and power analysis.

Loading component...

Reference

BIBTEXAcademic
@misc{samplesizeminimumdetectableeffectpowerpoweranalysismdecalculation, author = {Michael Brenndoerfer}, title = {Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation}, year = {2026}, url = {https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-01-01} }
APAAcademic
Michael Brenndoerfer (2026). Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation. Retrieved from https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies
MLAAcademic
Michael Brenndoerfer. "Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation." 2026. Web. today. <https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies>.
CHICAGOAcademic
Michael Brenndoerfer. "Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation." Accessed today. https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies.
HARVARDAcademic
Michael Brenndoerfer (2026) 'Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation'. Available at: https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies (Accessed: today).
SimpleBasic
Michael Brenndoerfer (2026). Sample Size, Minimum Detectable Effect & Power: Power Analysis & MDE Calculation. https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies
Direct link:
https://mbrenndoerfer.com/writing/sample-size-minimum-detectable-effect-power-analysis-mde-underpowered-studies