AWQ: Protecting Salient Weights for Efficient LLM Inference

In the previous chapter, we explored GPTQ's approach to quantization, which uses second-order Hessian information to minimize quantization error layer by layer. While GPTQ reaches impressive results, its reliance on expensive matrix inversions and sequential weight updates creates computational overhead that scales with model size. Activation-Aware Weight Quantization (AWQ) takes a fundamentally different approach: instead of trying to optimally quantize all weights, it focuses on identifying and protecting the small subset of weights that matter most for output quality.

The motivating question behind AWQ sounds simple: are all weights equally important? If you have a 7-billion parameter model and you need to quantize it to 4 bits, does every one of those seven billion numbers deserve the same level of careful treatment? Intuition says no. Some weights sit at important junctions in the network where small errors compound through many subsequent computations. Others contribute so little that even large errors in their values barely register in the final output. AWQ turns this intuition into a practical algorithm by identifying important weights and giving them preferential treatment under quantization.

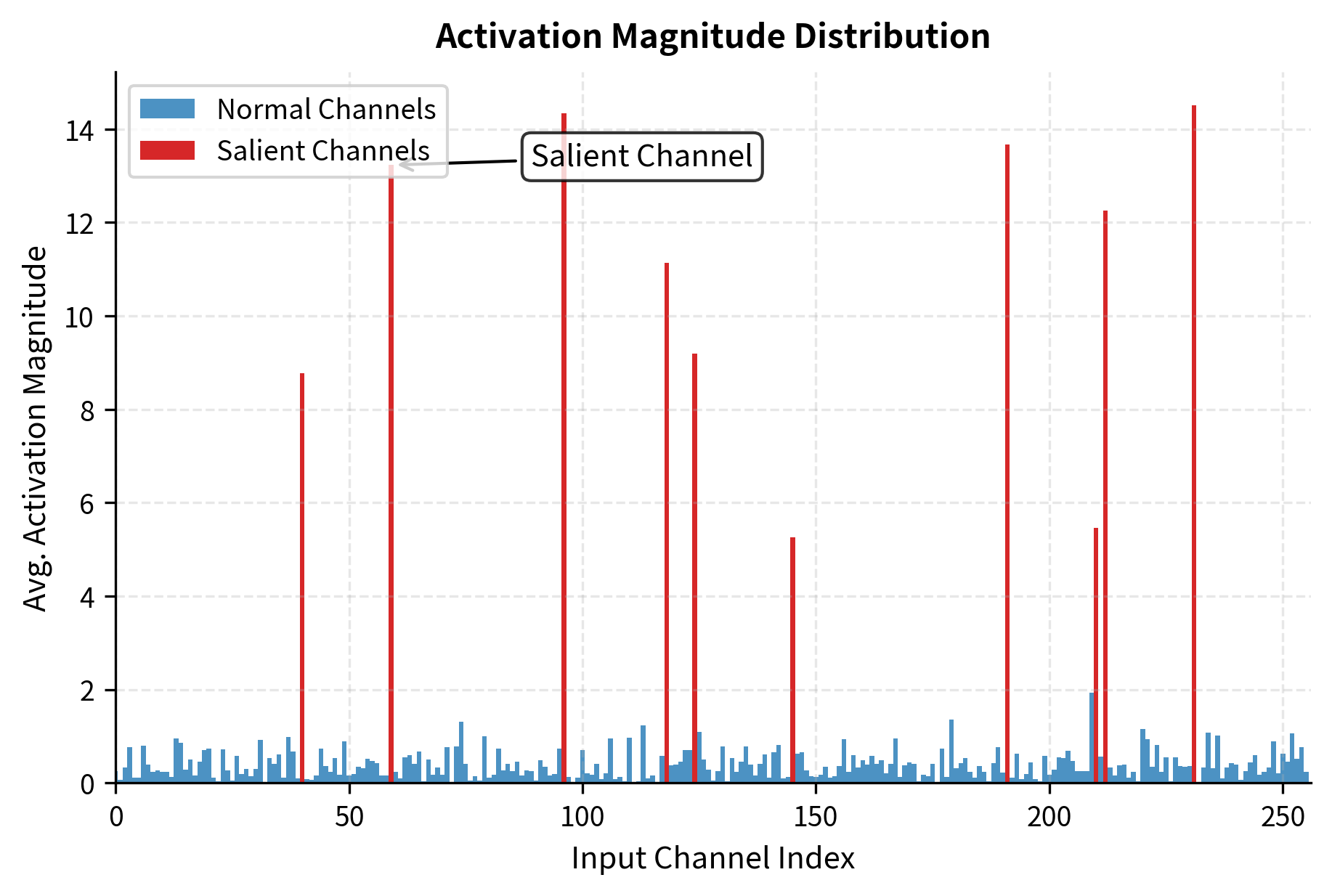
The mechanism AWQ uses to rank weights is elegant in its simplicity. Rather than computing expensive curvature information or running lengthy optimization procedures, AWQ looks at the activations that each weight multiplies. Think of it this way: a weight's importance depends on its own magnitude and on the magnitude of the signal it amplifies. A small weight that consistently multiplies large activations can have enormous influence on the output. A large weight that typically multiplies near-zero activations contributes almost nothing. By collecting activation statistics from a small calibration dataset, AWQ builds a picture of which input channels carry the most signal and therefore which weights deserve protection from quantization error.

AWQ protects the identified salient weights without changing their bit width. Naive approaches would keep important weights in higher precision, say 8 bits or 16 bits, while quantizing everything else to 4 bits. But this mixed-precision approach creates hardware headaches: kernels optimized for uniform 4-bit computation cannot efficiently process a mixture of precisions, and the irregular memory access patterns that result from mixed-precision weights degrade throughput. Instead, AWQ applies per-channel scaling factors that redistribute quantization precision. Important weights get scaled up before quantization, which effectively gives them finer resolution on the integer grid, and the inverse scaling is absorbed into the preceding layer. The final model is pure INT4, but the precision is concentrated where it matters.

This chapter builds on the quantization fundamentals from earlier sections and the specific techniques introduced in the GPTQ chapter. We will examine the theory of activation-aware quantization in depth, derive the scaling factor formula, walk through a concrete numerical example, and compare AWQ against GPTQ across multiple dimensions. By the end, you will have a thorough understanding of why AWQ works, when to prefer it over alternatives, and how to apply it in practice.

The observation underlying AWQ comes from analyzing weight and activation distributions in transformer models. To understand why some weights matter more than others, consider the forward pass through a neural network. Every linear layer performs a weighted sum of its inputs, but not all terms in that sum contribute equally to the final result.

Consider a linear layer computing the transformation:

where:

• $\mathbf{y}$: the output vector containing the results of the linear transformation
• $\mathbf{W}$: the weight matrix containing the layer's learnable parameters
• $\mathbf{x}$: the input activation vector representing the features from the previous layer

The contribution of weight $w_{ij}$ to output element $y_i$ is precisely $w_{ij} \cdot x_j$. This means a weight's actual impact on the output depends on its own magnitude and on the magnitude of the activation it multiplies. A weight with value 0.5 that consistently multiplies activations of magnitude 10 contributes far more to the output than a weight with value 2.0 that typically multiplies activations near zero. This observation forms the conceptual foundation of AWQ: the importance of a weight cannot be assessed in isolation but must be understood in the context of the activations it operates upon during real inference.

Think of it as the difference between a valve and a flow rate. The valve position (the weight) matters only in proportion to the water pressure behind it (the activation magnitude). A nearly closed valve on a high-pressure line can still let more water through than a wide-open valve on a trickle. Standard quantization treats all valves as equally important regardless of the pressure behind them. AWQ accounts for pressure.

Empirical analysis of large language models reveals that activation distributions are highly non-uniform across input channels. Some channels consistently produce large activations across many different inputs, while others typically remain near zero. This non-uniformity is not random; it shows the learned structure of the model, where certain feature dimensions have become more important during training. The model has, through the optimization process, channeled important information into specific dimensions while leaving others largely inactive.

This non-uniformity creates an opportunity for more intelligent quantization. If channel $j$ always has small activations, quantization errors in the weights connecting to that channel have minimal impact on the final computation. Even a large relative error in those weights produces a small absolute error in the output because the activation magnitude amplifying the error is tiny. But if channel $j$ consistently produces large activations, those weights are salient and require protection because any error in their representation will be amplified by the large activation values during every forward pass.

The key insight is that the actual harm caused by quantizing a weight is not the raw quantization error $|w - \hat{w}|$ but the output error $|w - \hat{w}| \cdot |x_j|$. Standard quantization minimizes the raw error uniformly. AWQ minimizes the output-weighted error, putting precision where the errors hurt most.

The simplest approach to protecting salient weights would be to keep them in higher precision, creating a mixed-precision representation where important weights use 8 or 16 bits while less important weights use 4 bits. However, mixed-precision schemes complicate hardware implementation and sacrifice some of the memory and speed benefits we seek from quantization. Inference kernels optimized for uniform 4-bit weights cannot efficiently handle a mix of precisions, and the irregular memory access patterns that result from mixed precision degrade performance. AWQ takes a more clever approach: it uses per-channel scaling factors to effectively "hide" more precision in the quantized representation for salient weights while maintaining a uniform bit width throughout the model.

To understand AWQ's approach, recall from our earlier discussion of quantization basics that the quantization error for a weight $w$ scales with the quantization step size. The step size determines how far apart adjacent representable values are in the quantized representation. When we quantize to $b$ bits with scale $s$, the maximum error is approximately $s/2$, since any real value can be at most half a step away from the nearest quantization level.

For a standard per-tensor or per-channel quantization scheme, the scale is determined by the range of values being quantized. Let the minimum and maximum weights in a group be $w_{\min}$ and $w_{\max}$. Then:

where:

• $s_q$: the quantization scale (step size), determining the distance between adjacent representable values in the integer grid
• $w_{\max}$: the maximum value in the weight tensor, defining the upper bound of the dynamic range
• $w_{\min}$: the minimum value in the weight tensor, defining the lower bound of the dynamic range
• $b$: the quantization bit width (4 for INT4 quantization)
• $2^b - 1$: the number of quantization intervals, which equals the maximum representable integer with $b$ bits

This formula reveals an important insight: the quantization error is determined by how much of the available integer range each weight occupies. Weights near the extremes of the distribution (close to $w_{\max}$ or $w_{\min}$) effectively receive finer resolution because they use more of the available quantization levels. Weights in the middle of the distribution share the interior levels and receive the same granularity. The range is the control point: changing the quantized range changes the resolution that all weights receive.

Now consider what happens when we multiply a weight by a constant $k > 1$ before quantization, then divide by $k$ after dequantization. The weight's contribution to the output is unchanged because the scaling operations cancel out exactly. But its quantization behavior shifts in a favorable way. The scaled weight $k \cdot w$ occupies proportionally more of the quantization range, effectively getting finer granularity in the discrete representation. When we dequantize and divide by $k$, the quantization error is also divided by $k$, meaning the effective error in the original weight space is reduced by the same factor $k$.

The catch is that scaling up one weight affects the overall range, potentially increasing quantization error for other weights in the same quantization group. If we scale up salient weights without adjusting anything else, the quantization scale $s_q$ increases to accommodate the larger values, and non-salient weights receive coarser quantization as a result. This is where the activation-awareness becomes important. If weight $w_{ij}$ multiplies activations that are on average $k$ times larger than typical, scaling that weight up by $k$ while scaling down the corresponding activation channel by $k$ preserves the computation while reducing quantization error for that salient weight. The inverse scaling on the activation side can be absorbed into preceding layers, making the transformation invisible at inference time.

Mathematically, for an input channel $j$, we can introduce a scaling factor $s_j$ applied to the weights while absorbing the inverse into the incoming activations:

where:

• $y_i$: the output value for neuron $i$, which remains mathematically unchanged
• $w_{ij}$: the original weight connecting input channel $j$ to output $i$
• $x_j$: the input activation at channel $j$
• $s_j$: the per-channel scaling factor applied to weights in column $j$
• $\tilde{w}_{ij} = w_{ij} \cdot s_j$: the scaled weight that will be quantized
• $\tilde{x}_j = x_j / s_j$: the inverse-scaled activation, which compensates for the weight scaling

The key insight is that we want $s_j$ to be larger for channels with larger typical activations, protecting those salient weights with more precision in the quantized representation. Channels with large activations have their weights scaled up, giving those weights more quantization levels to stand for fine-grained distinctions. Channels with small activations have their weights left mostly unchanged or scaled down slightly. The net effect is a redistribution of quantization precision from where it is wasted (low-activation channels where quantization errors barely affect outputs) to where it matters most (high-activation channels where the same error level would cause significant output distortion).

The inverse scaling $1/s_j$ applied to $\tilde{x}_j$ must be applied somewhere to preserve the original computation. In transformer models, AWQ handles this elegantly by fusing the inverse scaling into the preceding layer's normalization. Since LayerNorm and RMSNorm layers output directly to the input channels of the subsequent linear layer, multiplying the normalization scale by $1/s_j$ for each output channel reaches the needed compensation without adding any runtime overhead. At inference time, the model runs exactly as fast as a standard INT4 model with no extra computations.

AWQ determines optimal per-channel scaling factors by analyzing activation statistics from a small calibration dataset. Unlike GPTQ, which requires solving optimization problems involving Hessian matrices, AWQ relies on straightforward statistical measurements that can be computed efficiently in a single forward pass per calibration sample. The algorithm proceeds through four stages: activation collection, scale computation, weight transformation, and standard quantization.

Think of the overall algorithm as a three-phase engineering process. First, you diagnose the problem by measuring which channels carry the most signal. Second, you design a correction by computing scaling factors that shift quantization resolution toward those necessary channels. Third, you apply the correction by transforming the weights and absorbing the inverse transformation into the preceding layer. Each phase is simple on its own; the insight is in combining them.

The first step is running a calibration set through the model and recording activation statistics. This calibration set need not be large; typically a few hundred to a few thousand examples suffice to obtain stable estimates of activation magnitudes. For general-purpose language models, any diverse text corpus gives reliable statistics. For domain-specific models, calibration data from the target domain produces better results.

For each linear layer in the model, we record the average absolute magnitude of each input channel across the calibration examples. Formally, for a layer receiving inputs $x_j^{(n)}$ where $n$ indexes the calibration sample and $j$ indexes the input channel:

where:

• $\bar{a}_j$: the average activation magnitude for input channel $j$, serving as our proxy for channel importance during quantization
• $N$: the total number of calibration samples used to estimate statistics
• $x_j^{(n)}$: the activation value at channel $j$ for the $n$-th calibration sample
• $\left|x_j^{(n)}\right|$: the absolute magnitude, capturing signal strength regardless of sign (since both positive and negative activations amplify weight errors equally)

Taking the absolute value ensures we capture activation strength regardless of sign. A channel that alternates between large positive and large negative values is just as influential as one that is consistently large positive. Averaging across samples smooths out noise from individual examples and reveals the underlying pattern of which channels consistently carry strong signals across diverse inputs.

The averaging operation is important because any single input might happen to have unusual activation patterns. A question about chemistry might activate different channels than a question about sports. By averaging across many diverse examples, we obtain a stable estimate of each channel's typical importance under the model's actual usage distribution.

Given activation statistics, AWQ computes per-channel scaling factors that balance two competing objectives. The first objective is to protect salient weights: channels with large activations should receive larger scaling factors, expanding the weights to occupy more of the quantization range and thus receive finer resolution. The second objective is to avoid harming other weights: extreme scaling factors can hurt non-salient weights by compressing their share of the quantization range too aggressively, potentially causing larger errors than the uniform quantization they started with.

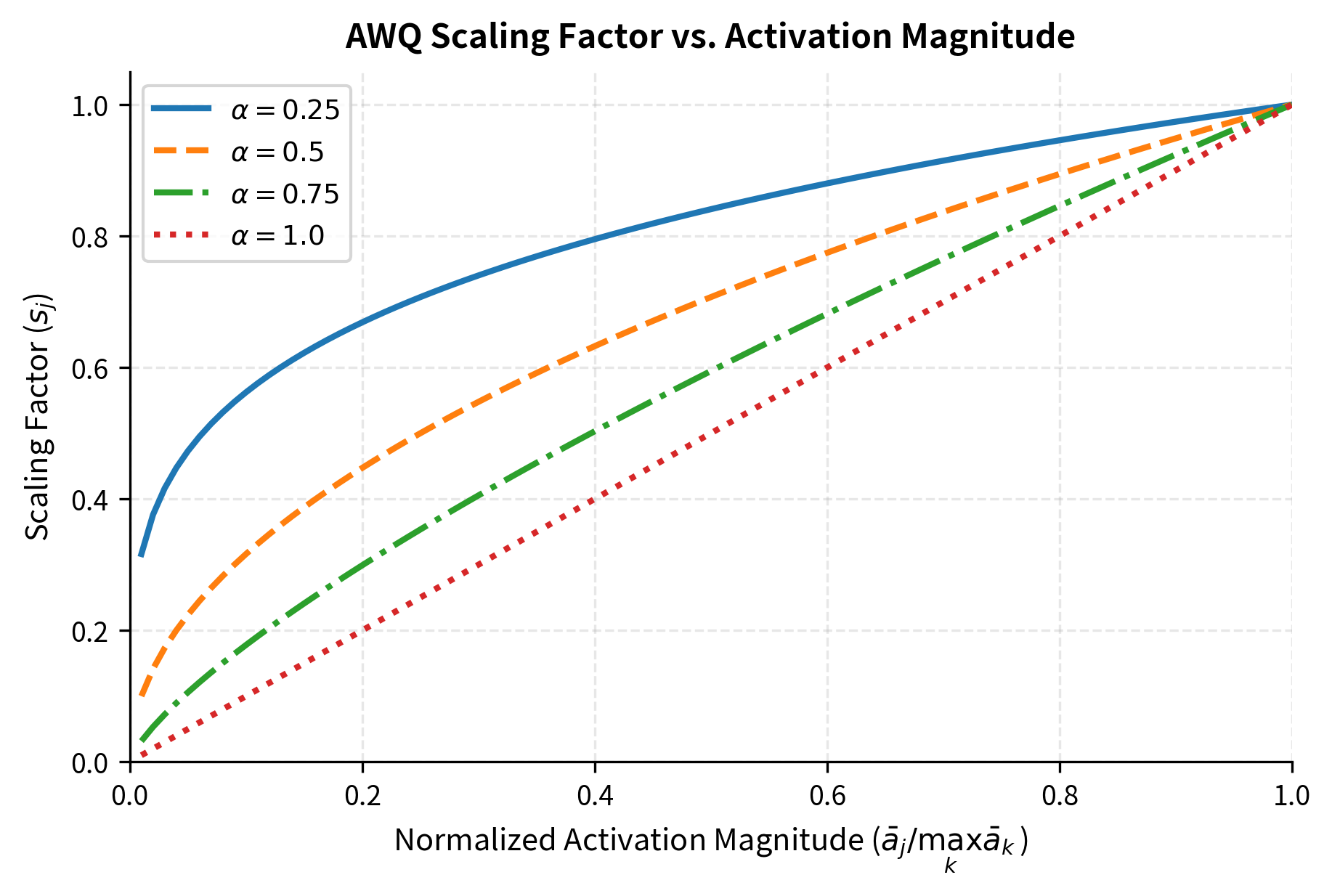
Finding the right balance requires a formula that increases with activation magnitude but does not grow too aggressively for the highest-activation channels. If the scaling factor is proportional to the raw activation magnitude and one channel has activations ten times larger than the average, that channel would receive a scaling factor ten times larger, which could severely compress the remaining channels. AWQ addresses this by normalizing activation magnitudes and raising them to a fractional power:

where:

• $s_j$: the calculated scaling factor for input channel $j$, which will multiply the weights in column $j$ of the weight matrix
• $\bar{a}_j$: the average activation magnitude for channel $j$, computed over the calibration set
• $\max_k \bar{a}_k$: the maximum average activation magnitude across all input channels $k$, serving as the normalization reference
• $\alpha$: a hyperparameter in the range $[0, 1]$ controlling scaling aggressiveness, balancing the protection of salient weights against potential distortion of others

The normalization by $\max_k \bar{a}_k$ ensures that scaling factors lie in the range $(0, 1]$. The channel with the largest average activation receives a scaling factor of exactly 1 (unchanged). Every other channel receives a scaling factor strictly less than 1, meaning their weights get compressed relative to the most important channel rather than expanded. This design ensures the overall quantization range does not grow, which would hurt all channels.

The exponent $\alpha$ gives a smooth tradeoff between the two objectives. When $\alpha = 0$, the formula yields $s_j = 1$ for all channels, and AWQ reduces to standard quantization without any activation-aware adjustment. When $\alpha = 1$, scaling factors are directly proportional to relative activation magnitudes. This gives maximum differentiation between channels. In practice, $\alpha$ values between 0.25 and 0.75 work well across different layer types, with the original AWQ paper using per-layer grid search to find optimal values.

When $\alpha = 0$, all scaling factors collapse to 1 (no adjustment), and AWQ reduces to standard quantization without any activation-aware optimization. When $\alpha = 1$, scaling factors are directly proportional to relative activation magnitudes. This gives maximum differentiation between channels. In practice, $\alpha$ values between 0.25 and 0.75 work well, with the original AWQ paper using grid search to find optimal values per layer.

The shape of these curves is significant. For low values of alpha, the curve is relatively flat, meaning even channels with quite low activation magnitudes receive nearly the same scaling as high-activation channels. This is a conservative setting that avoids hurting any channel but gives weaker protection for the salient ones. For higher alpha values, the curve bends more sharply, putting higher scaling factors on channels that truly dominate in activation magnitude while sharply reducing protection for mediocre channels.

With scaling factors computed, AWQ transforms the weights before applying standard quantization. The transformation is straightforward: for each input channel $j$, the corresponding column of the weight matrix is multiplied by the scaling factor $s_j$:

where:

• $\tilde{w}_{ij}$: the transformed (scaled) weight that will be fed into the quantization process
• $w_{ij}$: the original weight parameter from the pretrained model
• $s_j$: the scaling factor for channel $j$, expanding the weight's magnitude to utilize more of the quantization range

This multiplication stretches the weights for high-activation channels (those with $s_j$ close to 1) while compressing those for low-activation channels (those with small $s_j$). The resulting weight distribution concentrates the most important weights in a larger portion of the quantization range, where they benefit from finer resolution.

After applying channel scaling, AWQ applies standard group-wise INT4 quantization to the scaled weights. Within each quantization group (typically spanning 128 consecutive weights), the quantizer determines the scale $s_q$ and zero point $z$ that minimize quantization error for the group:

where:

• $\hat{w}_{ij}$: the integer-quantized weight stored in the 4-bit representation
• $\tilde{w}_{ij}$: the scaled weight being quantized
• $s_q$: the quantization scale for the weight group, mapping from real values to integers
• $z$: the zero point for asymmetric quantization, letting the integer grid to stand for asymmetric value ranges
• $\text{round}(\cdot)$: rounding to the nearest integer, which introduces quantization error

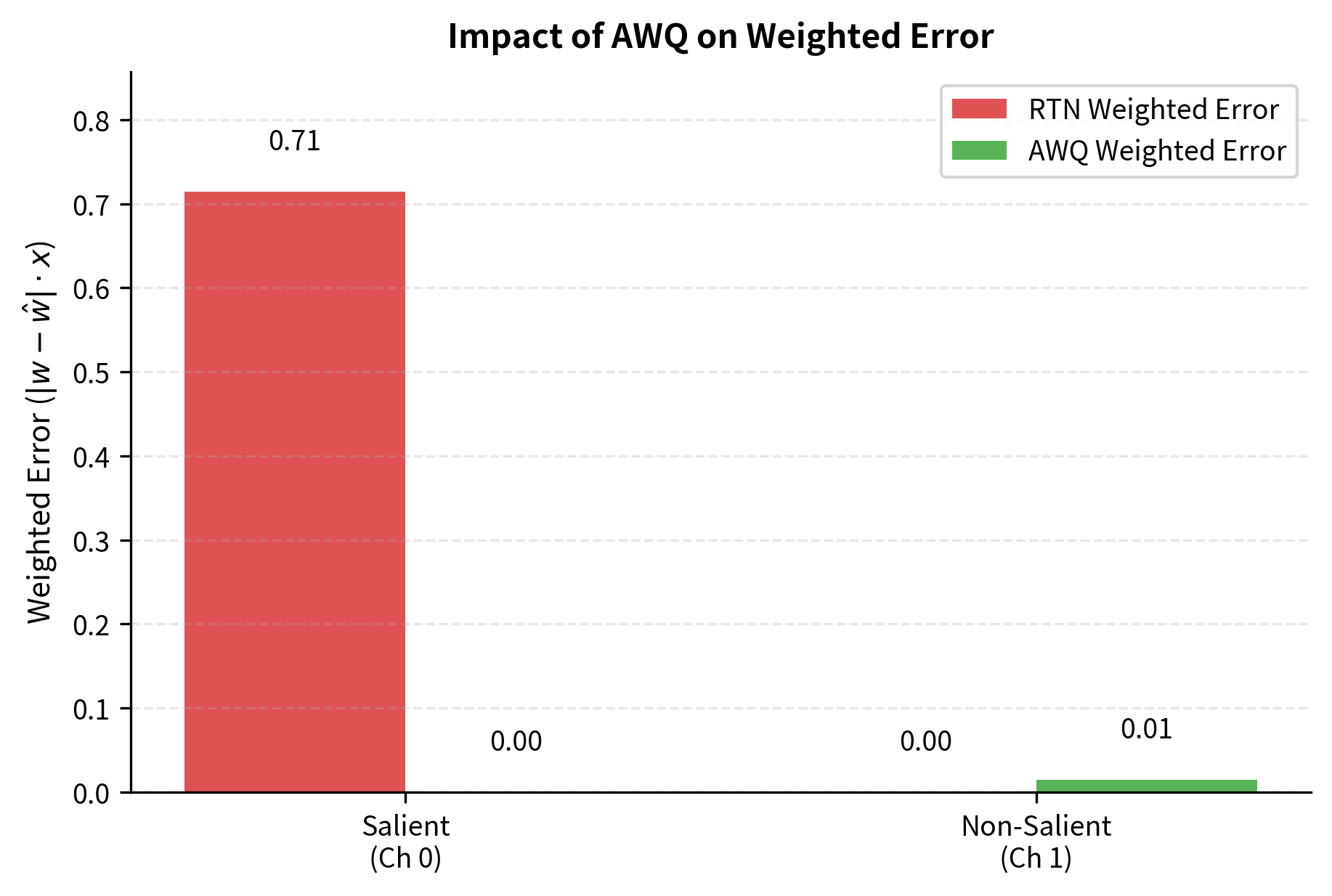
The rounding operation is where information is lost, as continuous values are mapped to the nearest point on a discrete grid with only $2^4 = 16$ representable levels. However, because salient weights have been scaled up relative to the group range, they now occupy proportionally more of those 16 levels and thus suffer less relative error.

During inference, weights are dequantized on-the-fly before use:

The inverse channel scaling then recovers the effective weight in the original computation space:

The effective quantization error for the original weight is therefore:

where:

• $\text{Error}_{ij}$: the effective quantization error in the original, unscaled weight space
• $\Delta_q$: the quantization step size for the group (approximately $s_q$), representing the minimum distinguishable difference in weight values
• $s_j$: the channel scaling factor; larger values reduce the effective error for that channel proportionally

For salient channels where $s_j$ is large (close to 1 after normalization by the maximum), the effective error is the base quantization step. For non-salient channels where $s_j$ is small, the error is larger, but these errors are multiplied by small activation values during inference and therefore have less impact on the output. The output error for element $y_i$ from channel $j$ is approximately $\text{Error}_{ij} \cdot |x_j|$, which equals approximately $(\Delta_q / s_j) \cdot |x_j|$.

The key insight of AWQ is now visible in the math. If $s_j$ is designed to be proportional to $\bar{a}_j$, then the output error contribution becomes approximately $\Delta_q \cdot |\bar{a}_j| / s_j \approx \Delta_q \cdot \text{const}$. AWQ redistributes quantization precision so that every channel contributes roughly equally to the total output error, rather than high-activation channels dominating the error.

While the formula-based scaling gives an excellent starting point, AWQ refines the scaling factors through a lightweight grid search over the exponent $\alpha$. The optimal value of $\alpha$ varies across layers depending on their specific weight and activation distributions. Layers in earlier parts of a network may have very different activation profiles than layers in later parts, and a single global $\alpha$ would be suboptimal for some.

For each layer, the grid search algorithm evaluates a small number of candidate $\alpha$ values, typically five to ten evenly spaced values between 0 and 1. For each candidate, it computes the corresponding scaling factors, transforms and quantizes the layer's weights, and evaluates quantization error by running the calibration data through that layer and measuring the mean squared error between the original and quantized outputs:

where:

• $\mathcal{L}(\alpha)$: the mean squared output error for a given scaling exponent $\alpha$
• $N$: the number of calibration samples
• $\mathbf{W}\mathbf{x}^{(n)}$: the original layer output for sample $n$
• $\hat{\mathbf{W}}(\alpha)\mathbf{x}^{(n)}$: the quantized layer output when using scaling factors derived from exponent $\alpha$
• $\left\|\cdot\right\|_2^2$: the squared Euclidean norm of the output error vector

The algorithm selects the $\alpha^*$ that minimizes $\mathcal{L}(\alpha)$ and uses the corresponding scaling factors for that layer. This per-layer optimization requires only a handful of forward passes through each layer, making the total additional cost negligible compared to the forward pass through the full model that happens anyway during activation collection.

This per-layer grid search adds minimal computational overhead since we're only searching over a handful of $\alpha$ values, unlike GPTQ's expensive Hessian computations. The search space is tiny, requiring only a few forward passes through each layer to evaluate the candidates. The resulting layer-specific $\alpha$ values allow AWQ to adapt to the heterogeneous structure of modern neural networks, where different layers may have very different activation and weight distributions. An attention query projection might benefit from more aggressive scaling than a feed-forward output projection, and the grid search discovers these differences automatically.

Let's trace the AWQ algorithm step by step through a minimal example to make the mathematics concrete. We will work with a tiny linear layer with just two input channels and show exactly how quantization error changes when we apply AWQ versus naive round-to-nearest quantization.

Setup. Consider a linear layer with a single-row weight matrix $\mathbf{w} = [0.5, 2.0]$ (one output, two inputs). Suppose the calibration dataset gives us average activation magnitudes $\bar{a}_0 = 10.0$ for channel 0 and $\bar{a}_1 = 0.1$ for channel 1.

Step 1: Identify salient channels. The maximum activation magnitude across channels is $\max_k \bar{a}_k = 10.0$ (channel 0). The normalized magnitudes are $\bar{a}_0 / 10.0 = 1.0$ and $\bar{a}_1 / 10.0 = 0.01$.

Step 2: Compute scaling factors with $\alpha = 0.5$. Applying the AWQ formula:

Channel 0 (the salient channel) gets scaling factor 1.0. Channel 1 (the non-salient channel) gets scaling factor 0.1.

Step 3: Transform weights. Multiply each weight by its channel's scaling factor:

After scaling, the transformed weights are $[0.5, 0.2]$. Notice that the max weight has dropped from 2.0 to 0.5 because we compressed the unimportant channel materially.

Step 4: Quantize the transformed weights. With a 3-bit symmetric quantizer (7 levels for simplicity), the quantization scale is:

Quantizing each transformed weight:

Step 5: Dequantize and undo channel scaling. The effective weights recovered after inverse scaling are:

Step 6: Compute weighted quantization error. The output-weighted errors are:

Comparison with RTN. Without AWQ, standard RTN quantizes the original weights $[0.5, 2.0]$ with scale $s_q = 2.0/3 \approx 0.667$:

The RTN weighted errors are:

The comparison is stark. RTN spends most of its quantization effort on channel 1 (the large weight) but channel 1 multiplies near-zero activations, so that accuracy is wasted. Meanwhile, channel 0 (the small weight that multiplies large activations) suffers a relative error of 33% that gets amplified by the activation magnitude of 10, creating an output error of 1.67. AWQ nearly eliminates this output error by giving channel 0 all the precision it needs, accepting a larger relative error on channel 1 where it barely matters.

This example captures the needed logic of AWQ in numerical form: precision is a resource to be allocated intelligently, not distributed uniformly.

Let's walk through a practical AWQ quantization using the AutoAWQ library, which implements the full AWQ algorithm with optimized CUDA kernels for inference.

The output confirms the successful creation of the quantized model directory, which now contains the compressed weights and configuration files needed for inference. The saved files include the INT4-packed weight tensors, quantization scales and zero points, and a configuration file describing the quantization parameters.

Once quantized, AWQ models load efficiently for inference. The AutoAWQ library gives optimized CUDA kernels that perform dequantization on-the-fly during matrix multiplication, avoiding the need to fully dequantize weights into memory.

The generated text shows that the 4-bit quantized model retains the linguistic capabilities of the original, creating coherent and contextually appropriate output despite the 4x compression. The fuse_layers=True option lets additional optimizations that combine sequential operations like dequantization and matrix multiply into single fused CUDA kernels, reducing memory bandwidth requirements and improving throughput further.

AWQ stores quantized weights in a packed format where multiple 4-bit values share INT32 storage. Let's examine the structure of a quantized layer to understand what is stored on disk and in memory.

The inspection reveals the internal structure of AWQ quantization: weights are packed eight-per-INT32 into the qweight tensor, while scales are kept in FP16 precision to preserve accurate dequantization. The compression ratio confirms the expected 4x reduction in weight memory usage compared to FP16. The scales and zero points occupy very little additional space because they are shared across groups of 128 weights.

Understanding AWQ's quantization parameters allows you to tune the algorithm for your specific model and deployment target. The most important parameters are:

• w_bit: The bit width for weight quantization. The standard choice is 4 bits (INT4), which gives a 4x compression ratio relative to FP16. Some deployments use 8 bits for higher accuracy with a 2x compression ratio, while aggressive compression targets use 3 bits at the cost of more accuracy degradation.

• q_group_size: The number of consecutive weights that share a single quantization scale and zero point. Smaller group sizes (e.g., 32 or 64) give finer-grained quantization with better accuracy but require more metadata storage. Larger group sizes (e.g., 256 or 512) reduce metadata overhead but may allow more quantization error. The value 128 is a commonly effective default that balances these concerns.

• zero_point: Whether to use asymmetric quantization (True) or symmetric (False). Asymmetric quantization with a zero point allows the integer grid to stand for values that are not centered at zero, which better handles weight distributions that are skewed. Most modern language model weights benefit from asymmetric quantization. Symmetric quantization is simpler and may be preferred on hardware that does not support efficient asymmetric dequantization.

• version: The kernel version for inference. "GEMM" kernels are optimized for general matrix multiplication and work well across a wide range of batch sizes and sequence lengths. "GEMV" kernels are specialized for single-vector multiplication (batch size 1) and give better throughput for interactive, low-latency use cases.

Both AWQ and GPTQ reach INT4 quantization with minimal accuracy loss, but they approach the problem from fundamentally different angles. Understanding these differences helps you choose the right method for your use case and deployment environment.

Both methods operate post-training without requiring any gradient updates or backpropagation. Both use a calibration dataset to obtain information about the model's behavior that guides quantization decisions. Both store weights in INT4 format with per-group scales for dequantization. Despite these surface similarities, the underlying algorithms reflect very different theories about what makes a quantization method good.

GPTQ, as we discussed in the previous chapter, treats quantization as an optimization problem. It uses second-order information from the Hessian of the output error with respect to the weights to determine how to round each weight to minimize overall squared error. Given that rounding one weight introduces error that changes the optimal rounding of subsequent weights, GPTQ iterates through the weight matrix column by column, adjusting remaining weights to compensate for quantization errors introduced so far. This approach is mathematically principled and finds near-optimal solutions within its framework, but computing and inverting the Hessian adds significant computational overhead.

AWQ takes an empirical, observation-driven approach. It recognizes that a small subset of weights dominates output quality and focuses protection on those weights. Rather than optimizing the quantization of each individual weight, AWQ optimizes the distribution of precision across weight channels by choosing appropriate scaling factors. The algorithm never needs to compute Hessians or solve optimization problems with thousands of variables. It makes one key observation (some channels matter more than others) and implements one key transformation (scale the weight columns to reflect this importance). The mathematical machinery is minimal, but the results are competitive.

Think of GPTQ as a skilled watchmaker who adjusts each gear individually while accounting for how each adjustment affects every other gear. AWQ is more like an engineer who identifies the critical components and uses better-grade materials only for those parts. The watchmaker may reach marginally finer tolerances on a good day, but the engineer works much faster and reaches similar reliability in practice.

GPTQ's layer-by-layer optimization with Hessian computation creates substantial overhead, particularly for larger models. Quantizing a 7B parameter model with GPTQ typically takes 30 to 60 minutes on a modern GPU. AWQ's simpler algorithm, based on activation statistics and grid search over a handful of scaling parameters, completes much faster, often 2 to 4 times quicker than GPTQ for the same model.

The speed difference becomes more pronounced as model size increases. For 70B parameter models, GPTQ can take many hours while AWQ completes in a fraction of that time. For 100B+ models, this difference becomes practically significant: researchers who need to iterate on quantization configurations or evaluate multiple checkpoints find AWQ's speed advantage very useful.

Both methods reach excellent accuracy retention, typically within 0.5 to 1 perplexity points of the original FP16 model when quantizing to INT4. Empirical comparisons show they perform similarly across a range of standard benchmarks:

AWQ often edges out GPTQ slightly on perplexity benchmarks, though differences are within noise margins. The more significant accuracy advantage of AWQ emerges in out-of-distribution scenarios: AWQ's activation-based importance estimation generalizes better to inputs outside the calibration distribution. Because GPTQ optimizes so carefully for the specific calibration samples, it can slightly overfit to that distribution, while AWQ's simpler statistical approach captures more reliable importance signals.

GPTQ has been available longer and has broader kernel support across different hardware platforms. Libraries like llama.cpp, ExLlama, and text-generation-inference all support GPTQ formats with highly optimized kernels accumulated over years of community development.

AWQ kernels are newer but have been rapidly adopted. The AutoAWQ library gives optimized CUDA kernels, and major inference frameworks including vLLM and TensorRT-LLM now include AWQ support. AWQ's simpler weight transformation (per-channel scaling rather than arbitrary compensatory updates) makes kernel implementation more straightforward, which has accelerated ecosystem adoption. The format is also more amenable to hardware acceleration beyond CUDA, as the dequantization pattern is regular and predictable.

Choose GPTQ when:

• You need maximum compatibility with existing inference infrastructure, particularly llama.cpp or ExLlama
• You are willing to spend more time on quantization for potentially marginal improvements on specific tasks
• You are quantizing smaller models where quantization time is not a bottleneck

Choose AWQ when:

• You are quantizing very large models (65B+) and quantization time matters
• You need reliable accuracy across diverse input distributions, including out-of-distribution inputs
• You are deploying on platforms with strong AWQ kernel support such as vLLM or TensorRT-LLM
• You want a simpler, faster quantization workflow without sacrificing accuracy

AWQ gives several advantages that make it particularly attractive for deploying large language models in resource-constrained environments. Understanding these benefits in concrete terms helps you make informed deployment decisions and set realistic expectations for the performance gains you will see.

Like other INT4 quantization methods, AWQ reduces model memory footprint by approximately 4x compared to FP16. A 7B parameter model drops from roughly 14 GB to roughly 4 GB, letting deployment on consumer GPUs with 8 GB of VRAM that previously could not run such models at all. A 13B model drops from about 26 GB to about 7 GB, fitting on a single 8 GB consumer GPU. A 70B model drops from roughly 140 GB to roughly 40 GB, which makes it accessible on high-end professional GPUs with 48 GB of VRAM rather than requiring multi-GPU clusters.

The memory savings extend beyond weight storage. AWQ's per-channel scaling transformation adds minimal metadata overhead compared to methods that store additional per-weight correction terms. The scales and zero points required for group-wise quantization (one scale and one zero point per 128 weights) typically add only 0.5 to 1% to the compressed model size. The total overhead is negligible compared to the 4x savings on the weights themselves.

These memory savings have cascading benefits during inference. With a smaller memory footprint, the model fits in the GPU's L2 cache and HBM bandwidth bucket more efficiently. More of the available VRAM can be used for the KV cache during generation, letting longer contexts or larger batch sizes. On memory-constrained systems, the difference between fitting a model and not fitting it at all is the difference between deployment and infeasibility.

AWQ reaches throughput improvements of 1.5x to 3x over FP16 inference on modern GPUs, depending on the specific hardware and model architecture. These speedups come from two primary sources.

The first source is reduced memory bandwidth consumption. During autoregressive generation, reading the model's weights from GPU HBM memory is often the bottleneck, not floating-point computation. Modern GPUs have orders of magnitude more FLOP/s than memory bandwidth. When a matrix multiplication reads weights from memory at 4 bits per weight instead of 16 bits per weight, it saturates the memory bus 4x less frequently, letting the same computation to complete in less time. This bandwidth argument explains why quantization often delivers more than a proportional speedup: the model is smaller and the computation becomes less memory-bound.

The second source is the efficiency of the dequantization kernels. AWQ's per-channel scaling maps cleanly to tensor operations. The dequantization at inference time unpacks 4-bit integers, applies a group scale and zero point, and optionally adjusts by the channel inverse scaling factor (if not already fused into the preceding layer). These operations follow a predictable structure that can be parallelized efficiently, making them amenable to highly optimized CUDA implementations. Fused kernel implementations that combine dequantization with the subsequent matrix multiply avoid materializing the full FP16 weight matrix in memory at all, maintaining the memory bandwidth advantage throughout.

The actual speedup depends heavily on your inference setup. Memory-bound scenarios (large batch sizes, long sequences, limited GPU memory bandwidth) see the largest improvements. Compute-bound scenarios with very large matrices and unlimited memory see smaller but still significant gains from the reduced model size.

AWQ requires only a small calibration dataset, typically 128 to 512 samples, to compute reliable activation statistics. The algorithm is reliable to the specific calibration samples chosen, as it uses only channel-wise average magnitudes rather than sample-specific optimization targets. This contrasts with methods that use calibration data for layer-wise output reconstruction, where the specific choice of samples can affect results more strongly.

However, the calibration data should still be representative of the model's intended use case. Quantizing a code generation model using only English prose samples may not yield optimal results for code completion tasks, since activation patterns differ between natural language and code. For domain-specific deployments, using calibration data from the target domain or task consistently produces better results than using generic text. The difference is rarely large but can be real for specialized applications.

AWQ's activation-awareness, while powerful, rests on assumptions that do not always hold. Understanding these limitations helps you anticipate when AWQ might underperform and how to mitigate potential issues.

The most basic limitation is that AWQ's saliency metric (average activation magnitude across a calibration set) is a statistical proxy for weight importance, not a direct measure of it. A weight might be necessary to the model's performance but happen to see moderate activation magnitudes on the calibration set. This can occur when the model handles certain input patterns rarely but critically, and those patterns are not well-represented in the calibration data. For example, a model that is occasionally called upon to solve a specific type of math problem might have weights that activate strongly for that pattern but appear dormant in a general-purpose calibration corpus. AWQ would not protect those weights, and performance on math problems might degrade more than on general text.

This calibration-distribution mismatch can also arise from domain shift. If a model is quantized using English text but deployed on multilingual inputs, the activation patterns for non-English languages may identify different channels as salient than the English calibration data would suggest. Similarly, if a model is fine-tuned after quantization or evaluated on tasks that differ substantially from the calibration distribution, the per-channel scaling factors optimized for the calibration distribution may be suboptimal for the deployment setting.

AWQ's per-channel scaling formulation also captures only one dimension of weight importance: the column-wise activation magnitude. In reality, weight saliency can be more complex. GPTQ's Hessian-based approach captures second-order interactions between weights, identifying cases where quantizing one weight affects the optimal treatment of another. AWQ has no mechanism for detecting these cross-weight dependencies. In practice this limitation is minor for most models and tasks, because the dominant factor in weight importance is indeed the activation magnitude of the corresponding input channel. But for models with unusual weight structure or highly correlated weight patterns, GPTQ's more complete analysis can occasionally give better results.

Additionally, AWQ's scaling factors are computed once at quantization time and fixed thereafter. If the model's effective activation distribution shifts during inference (due to input distribution shift, prompt engineering, or special tokens), the pre-computed scaling factors may no longer be optimal. This is a limitation shared by all static post-training quantization methods, but it is worth keeping in mind for deployments where the input distribution is expected to be very different from anything in the calibration set.

Finally, AWQ gives per-channel scaling at the granularity of input channels to linear layers. It does not address quantization artifacts in activations themselves (activation quantization), in embedding tables, or in the logit computation. For deployments targeting extremely low precision (below 4 bits) or requiring very tight accuracy guarantees, additional techniques such as activation quantization or outlier suppression may be needed in combination with AWQ.

For most practical deployments, these limitations are minor. AWQ performs well across diverse models and tasks, and its speed and simplicity make it a practical default for INT4 weight quantization.

AWQ is a shift in quantization philosophy, from optimizing all weights equally to protecting the small subset that matters most. This chapter covered:

Salient weight identification. AWQ observes that weights multiplying large activations have disproportionate impact on model outputs. By analyzing activation magnitudes from a calibration dataset, it identifies which weights deserve protection from quantization error. The saliency metric is simple: average absolute activation magnitude across the calibration set.

Per-channel scaling. Rather than keeping salient weights at higher precision, AWQ uses per-channel scaling factors to effectively give them more resolution in the quantized representation. Weights are scaled up before quantization, which stretches them to occupy more of the INT4 grid. The inverse scaling is fused into preceding layers so inference runs at uniform INT4 precision with no extra operations.

The scaling formula. The scaling exponent $\alpha$ controls how aggressively AWQ differentiates between salient and non-salient channels. Small $\alpha$ values give gentle, broadly uniform scaling. Large $\alpha$ values give strong protection for the highest-activation channels. Per-layer grid search finds the optimal $\alpha$ efficiently.

Efficient algorithm. AWQ avoids GPTQ's expensive Hessian computations in favor of simple activation statistics and grid search over a handful of scaling hyperparameters per layer. This makes possible faster quantization of large models, often 2 to 4 times faster than GPTQ on comparable hardware.

Practical tradeoffs. AWQ and GPTQ reach similar accuracy on standard benchmarks, but AWQ often generalizes better to out-of-distribution inputs because its saliency estimates are based on reliable statistical measurements rather than sample-specific optimization. GPTQ has broader ecosystem support due to its earlier release, but AWQ is rapidly gaining adoption across major inference frameworks.

The next chapter explores the GGUF format, which gives a standardized way to store and distribute quantized models across different inference engines and hardware platforms.

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about Activation-aware Weight Quantization (AWQ).