Part of Language AI Handbook
Covers INT4 quantization techniques for LLMs. Topics include group-wise quantization, NF4 format, double quantization.
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Article links
Make inline references clickable
INT4 Quantization
The GPU memory requirements for large language models create a basic access problem. A 70-billion-parameter model in standard 16-bit floating-point format consumes roughly 140 GB of GPU memory, an amount that requires several A100 or H100 GPUs costing tens of thousands of dollars to purchase. For most researchers and practitioners, that puts frontier-scale models out of reach entirely. Quantization is the most powerful tool we have for closing this gap, and INT4 quantization in particular has enabled a remarkable democratization of LLM inference: models that once required a data center now run on consumer GPUs that cost a few hundred dollars.
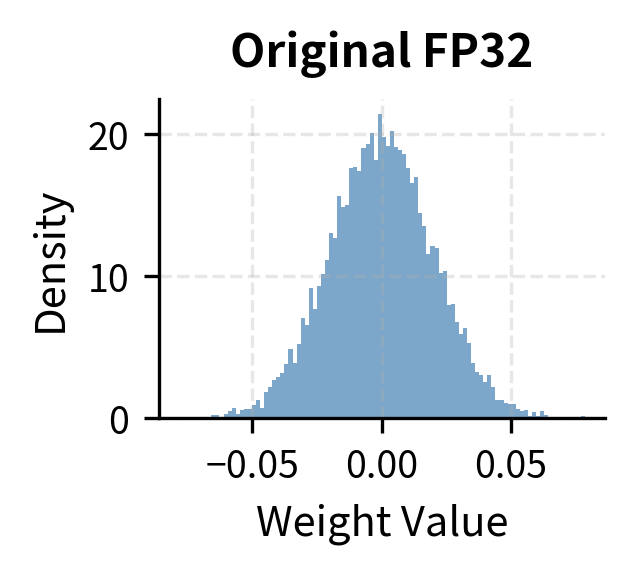
Reducing weights from 16 bits to 8 bits cuts memory in half while preserving most model quality. The natural question is: can we go further? INT4 quantization promises to halve memory again, fitting a 70B parameter model into roughly 35 GB instead of 140 GB. But moving from 8 bits to 4 bits is not just "more of the same." It introduces basic challenges that require entirely new techniques to overcome. The step from INT8 to INT4 is qualitatively different from the step from FP16 to INT8, because 4-bit precision is so coarse that naive approaches simply destroy model quality.
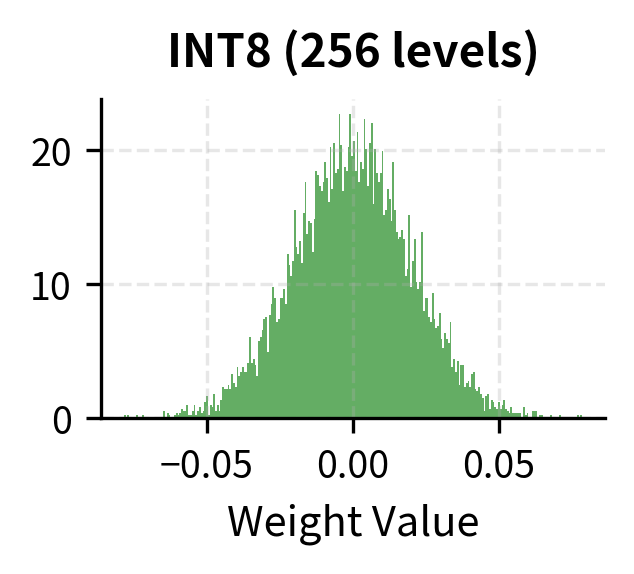
As we discussed in the previous chapter on INT8 quantization, the basic idea of quantization is mapping continuous floating-point values to a discrete set of integers. INT8 gives us 256 possible values. INT4 gives us only 16. This dramatic reduction in representational capacity means that naive 4-bit quantization produces models that perform worse than much smaller models in full precision. The techniques we explore in this chapter, particularly group-wise quantization and specialized 4-bit formats like NF4, are what make aggressive quantization practical rather than destructive.
Think of quantization as converting a high-resolution photograph to a low-resolution thumbnail. Going from 16-bit to 8-bit is like reducing a 4K image to 1080p: you lose some detail, but the image remains clear and recognizable. Going from 8-bit to 4-bit is like reducing that 1080p image to 64x64 pixels: without special techniques, faces become unrecognizable blobs. The techniques in this chapter are like smart compression algorithms that identify which pixels carry the most information and preserve them at higher fidelity, making even the 64x64 version surprisingly usable.
This chapter builds on the group quantization concepts from our INT8 discussion and introduces three key innovations that make 4-bit quantization viable: group-wise scaling that isolates the damage from outliers, the NF4 (Normal Float 4) format that places quantization levels optimally for Gaussian-distributed weights, and double quantization that reduces the overhead from storing scale factors. Together, these ideas underpin systems like QLoRA and bitsandbytes, which have brought 70B-scale inference to consumer hardware. We also walk through a complete numerical worked example so you can trace exactly how a weight survives the round-trip from FP16 to INT4 and back.
For most of the 2010s, post-training quantization research focused on INT8, which was already considered aggressive. The idea of running production models at 4-bit precision seemed impractical: early attempts produced models with catastrophically degraded quality. The breakthrough came in 2022 and 2023, driven by the urgent demand to run increasingly large models on affordable hardware. The GPTQ paper (Frantar et al., 2022) showed that second-order information could guide 4-bit quantization to near-lossless quality for large models. The QLoRA paper (Dettmers et al., 2023) introduced NF4 and double quantization, along with the bitsandbytes library that made 4-bit inference accessible with a few lines of Python. The LLM.int8() paper by the same group had previously shown that INT8 worked well, and QLoRA extended this work to demonstrate that 4-bit quantization combined with LoRA fine-tuning could match full-precision fine-tuning on many benchmarks. These papers transformed INT4 from a research curiosity into a standard deployment tool.
The Challenge of 4-Bit Precision
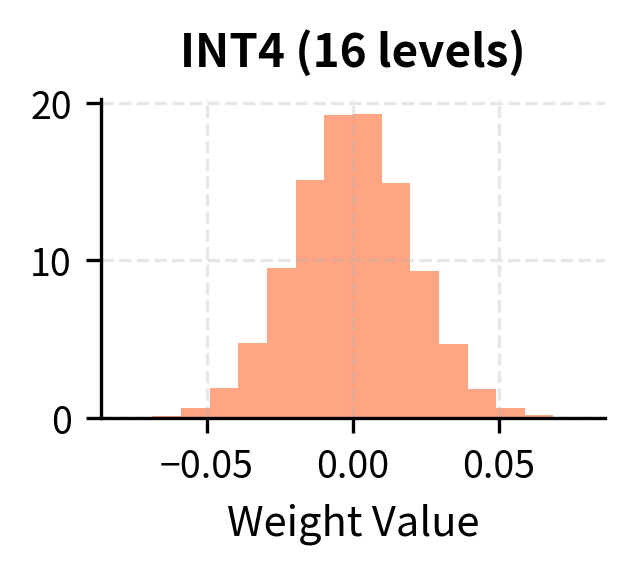
Understanding why 4-bit quantization is hard requires understanding what those 16 levels mean in practice. With only 4 bits, we can represent just 16 distinct values, and every weight in the neural network must map to exactly one of these 16 values. To understand why this limitation is so severe, consider the basic mathematics at play. If we use signed integers, this gives us a range from -8 to 7 (or -7 to 7 with a symmetric scheme). Every weight in a neural network, regardless of its original floating-point precision, must map to one of these 16 values. This is an extremely coarse discretization of the original continuous space, and the consequences propagate through every matrix multiplication in the model.
Think of it this way: INT4 quantization is like trying to represent every color in a photograph using only 16 distinct shades. A grayscale photograph with 256 shades (INT8) already loses some detail, but you can still recognize faces and read text. With only 16 shades, fine details merge together and subtle distinctions disappear. For neural network weights, those subtle distinctions between similar-but-not-identical small weights are precisely what encode the model's learned knowledge, and losing them changes model behavior in unpredictable ways.
Consider what this means for a typical weight distribution. Neural network weights after training often follow an approximately normal distribution centered near zero. The majority of weights cluster around small magnitudes, with the distribution tapering off symmetrically toward the tails. With INT8, we have enough resolution to capture the shape of this distribution reasonably well, since 256 quantization levels can provide fine granularity even in the densely populated region near zero. With INT4, we are essentially creating a 16-bucket histogram to represent a continuous distribution. Each bucket must absorb a wide swath of the original weight values, collapsing potentially meaningful differences into a single quantized output.
When we quantize a value, we introduce a quantization error equal to the difference between the original value and its quantized representation. With 256 levels, the maximum error for any single weight is bounded by half the step size between adjacent levels. With only 16 levels, that step size becomes 16 times larger, and the maximum quantization error grows proportionally. This error propagates through every matrix multiplication in the network, accumulating and potentially compounding in ways that can fundamentally alter the model's behavior. The errors are not random noise that averages out: they are systematic biases that can shift the model's predictions in consistent but unexpected directions.
The key insight is that the severity of quantization error depends on how many levels are available and how well those levels match the data distribution. Most of the problems with naive 4-bit quantization stem from a mismatch: the quantization grid is designed for uniform data, but neural network weights are emphatically non-uniform. This mismatch motivates both the group-wise approach (which adapts the scale locally) and the NF4 format (which adapts the level placement globally).
import numpy as np
# Simulate a typical neural network weight distribution deterministically
weight_rng = np.random.default_rng(42)
weights = weight_rng.standard_normal(10000) * 0.02 # Typical small weight scale
# What INT8 and INT4 quantization "see"
int8_bins = 256
int4_bins = 16
The loss of precision becomes more severe when we consider outliers. Recall from our INT8 discussion that neural networks often have a small number of outlier weights with magnitudes much larger than the majority. These outliers, though rare, can be critically important for the model's computations, often encoding strong feature responses or needed biases. With INT8, we can absorb some outlier impact because we have 256 levels to work with. This provides reasonable resolution even after accommodating extreme values. With INT4, outliers become catastrophic because the limited number of levels cannot simultaneously span a wide range and maintain adequate precision in the dense central region.
The Outlier Problem Intensified
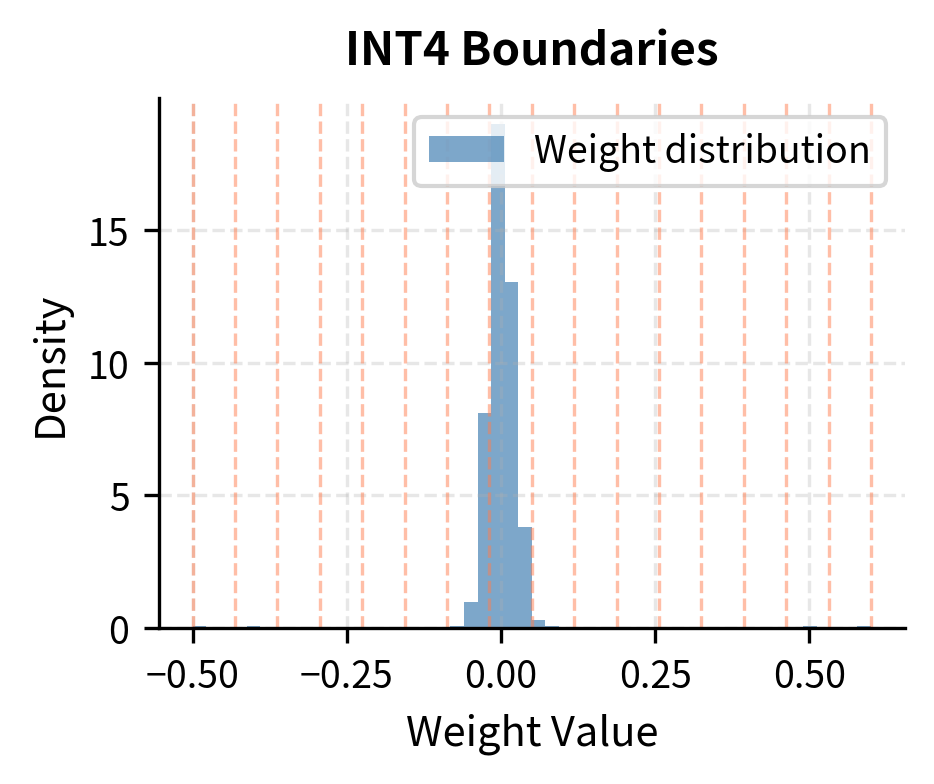
To build intuition for why outliers cause such severe problems at 4-bit precision, imagine a layer where 99% of weights fall between -0.1 and 0.1, but a few outliers reach values of 0.5 or higher. If we set our quantization range to cover the outliers, most of our 16 quantization levels will be "wasted" on the outlier range, leaving very few levels to distinguish the majority of weights near zero. This is a basic trade-off that becomes increasingly painful as the number of available levels decreases.
Think of this problem as a zoom lens on a camera. If your frame must fit both a distant mountain and a nearby flower, the flower becomes just a few indistinct pixels. The "zoom level" of your quantization scale is forced to accommodate the most extreme value, compressing everything else into a tiny slice of your available range. With 256 levels (INT8), you still have reasonable detail on the flower even when the mountain is in frame. With 16 levels (INT4), the flower becomes essentially invisible.
Consider the mathematics of this trade-off. Suppose our 16 quantization levels must span from -0.5 to 0.5 to accommodate outliers. The step size between adjacent levels is then 1.0 divided by 15 (since we have 16 levels creating 15 intervals), giving approximately 0.067 per step. For the 99% of weights living in the range of -0.1 to 0.1, this means they have access to only about 3 distinct quantization levels. The subtle differences between small weights, which are important for model computations, are lost in the coarseness imposed by the outliers.
More formally, for symmetric quantization, the scale factor is determined by the maximum absolute value in the tensor:
where:
- : the vector of weights being quantized
- : the maximum absolute value across all weights in the group
- : the maximum representable integer (7 for signed INT4 with range -7 to 7)
A single outlier weight with magnitude 0.6 among thousands of weights with magnitude 0.02 forces . For a weight of 0.02, the quantized index is . Nearly every small weight gets mapped to integer 0, making them indistinguishable from each other and from true zeros. The entire information content of the small-weight region collapses to a single point.
# Demonstrate outlier impact on INT4 quantization
outlier_rng = np.random.default_rng(42)
# Normal weights with a few outliers
normal_weights = outlier_rng.standard_normal(1000) * 0.02
outliers = np.array([0.5, -0.4, 0.6, -0.5]) # Just 4 outliers
weights_with_outliers = np.concatenate([normal_weights, outliers])
# Uniform quantization across full range
w_min, w_max = weights_with_outliers.min(), weights_with_outliers.max()
scale = (w_max - w_min) / 15 # 16 levels (0-15) for unsigned INT4
def quantize_uniform(weights, scale, w_min):
"""Uniform quantization to 4-bit range (0-15)"""
q = np.round((weights - w_min) / scale).astype(int)
q = np.clip(q, 0, 15)
return q
def dequantize_uniform(q, scale, w_min):
"""Dequantize back to float"""
return q * scale + w_min
q_weights = quantize_uniform(weights_with_outliers, scale, w_min)
reconstructed = dequantize_uniform(q_weights, scale, w_min)
# Calculate error metrics
mse = np.mean((weights_with_outliers - reconstructed) ** 2)
max_error = np.max(np.abs(weights_with_outliers - reconstructed))Weight range: [-0.5000, 0.6000] Scale factor: 0.073333 Mean squared error: 0.00039370 Maximum error: 0.036582 Number of unique quantized values used: 7
With a scale of approximately 0.07, each quantization step is large relative to our typical weights near zero. Most small weights get mapped to the same few quantization levels, destroying the subtle differences between them. The quantization process discards the details that distinguish small weights, even though these differences affect inference. Notice also how few unique quantized values appear: with 1004 weights and 16 possible levels, we would expect all 16 to be used, but outliers force most values into just a handful of central bins.
Group-Wise Quantization
The solution to the outlier problem at 4-bit precision is group-wise quantization, also called block-wise quantization. This technique represents a major change in how we approach the quantization problem: instead of asking "what single scale factor best represents this entire weight matrix?" we ask "what scale factor best represents each small neighborhood of weights?" Instead of using a single scale factor for an entire tensor or even a channel, we divide weights into small groups and compute separate scale factors for each group. This localized approach isolates the impact of outliers, preventing them from corrupting the quantization of the entire weight matrix.
Think of group-wise quantization as applying a different "zoom level" to different regions of the weight matrix. The parts of the matrix that contain mostly small, closely clustered weights get a fine-grained zoom that can distinguish subtle differences. The parts that happen to contain outliers get a wider zoom to accommodate them, but only those parts are affected. The rest of the matrix continues to benefit from fine resolution, oblivious to the outliers elsewhere.
This approach works because of a key statistical fact about how outliers appear in trained neural networks. Outlier weights do not distribute themselves uniformly throughout a weight matrix. They appear sporadically, concentrated in particular rows, columns, or small regions. When they do appear, they are surrounded by many non-outlier weights that have similar small magnitudes. By working with groups of 32, 64, or 128 consecutive weights, we ensure that any given group likely contains either zero or a small number of outliers. The groups containing outliers sacrifice precision for range; the groups without outliers maintain fine-grained precision. This spatial separation of outlier influence is the core mechanism that makes group-wise quantization so effective.
The memory overhead of group-wise quantization is modest and well-controlled. Each group requires one additional scale factor, typically stored in FP16 (16 bits). For a group of 128 weights, this adds 16 bits amortized over 128 four-bit weights, which is extra bits per weight. The total effective bit rate becomes bits per weight, barely above the nominal INT4 rate. As we will see with double quantization later in this chapter, even this small overhead can be further reduced.
The Group Quantization Concept
To understand why group-wise quantization works so effectively, consider the spatial distribution of outliers within a weight tensor. In trained neural networks, outliers typically do not occur uniformly throughout a tensor. Instead, they appear sporadically, concentrated in certain locations while leaving large regions of the tensor relatively outlier-free. By using small groups, an outlier affects only the quantization of its own group, not the entire layer. The remaining groups, free from outlier contamination, can use their 16 quantization levels efficiently to represent their local weight distribution with high fidelity.
For a weight tensor, group-wise quantization proceeds through the following steps:
- Divide the weights into groups of size , where common choices are 32, 64, or 128 elements per group
- Compute a separate scale factor (and optionally zero-point) for each group based only on the weights within that group
- Quantize each group independently using its own scale factor
The key insight is statistical: within any sufficiently small group of weights, the probability of encountering an extreme outlier is much lower than across the entire tensor. When an outlier does appear in a group, it affects only the weights in that group, leaving the thousands or millions of other weights in the tensor unaffected. Containing outlier damage makes 4-bit quantization practical.
The formal description of group-wise symmetric quantization is straightforward. For a group of weights , we compute:
where:
- : the scale factor for group , computed from the weights in that group only
- : the maximum absolute weight value within the group
- : the maximum representable integer (7 for signed INT4 with range -7 to 7)
- : the quantized integer representation of weight
- : rounding to the nearest integer
- : clamping to the valid integer range
Reconstruction is simply the inverse operation: . The stored representation is the collection of integers along with the per-group scale factors .
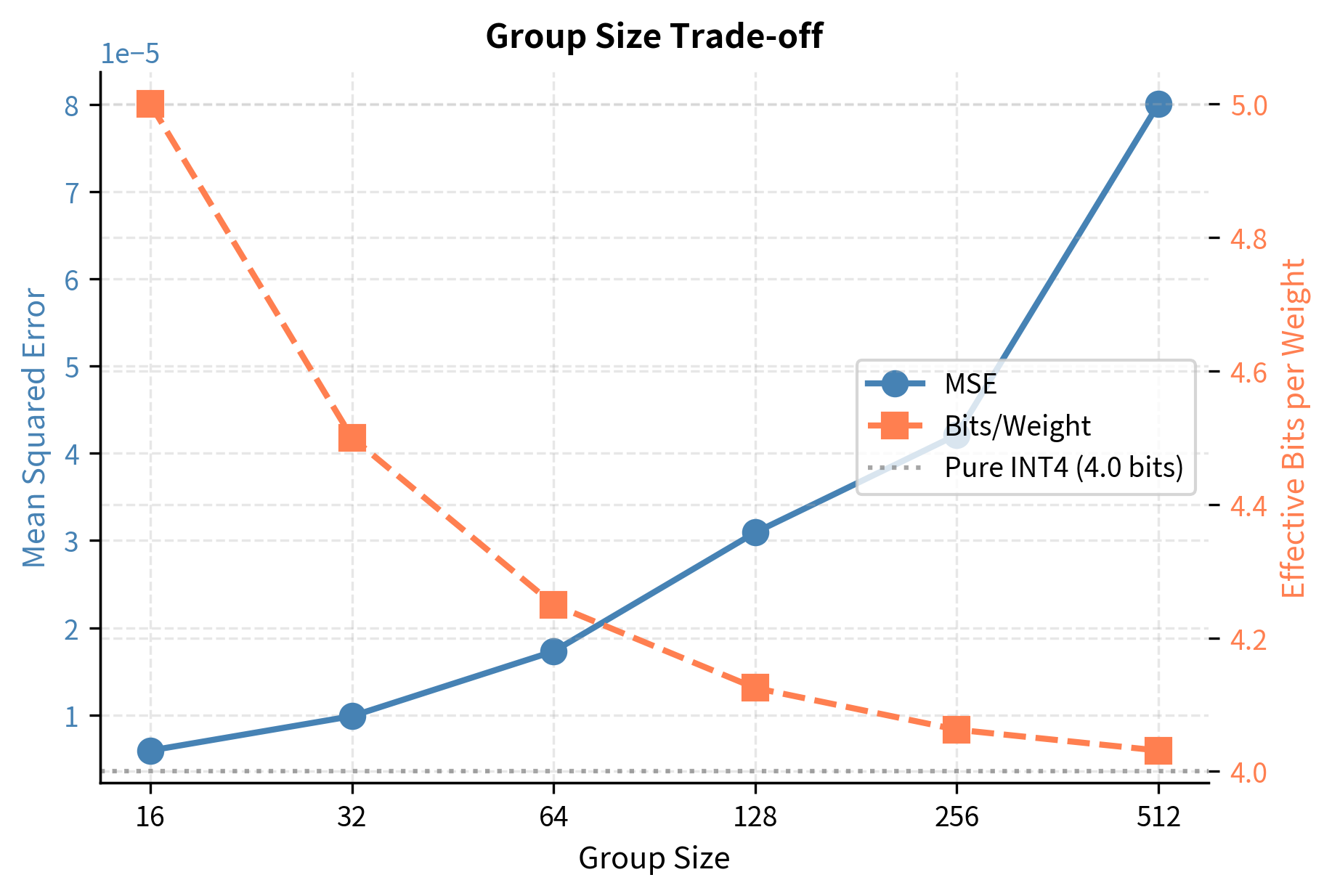
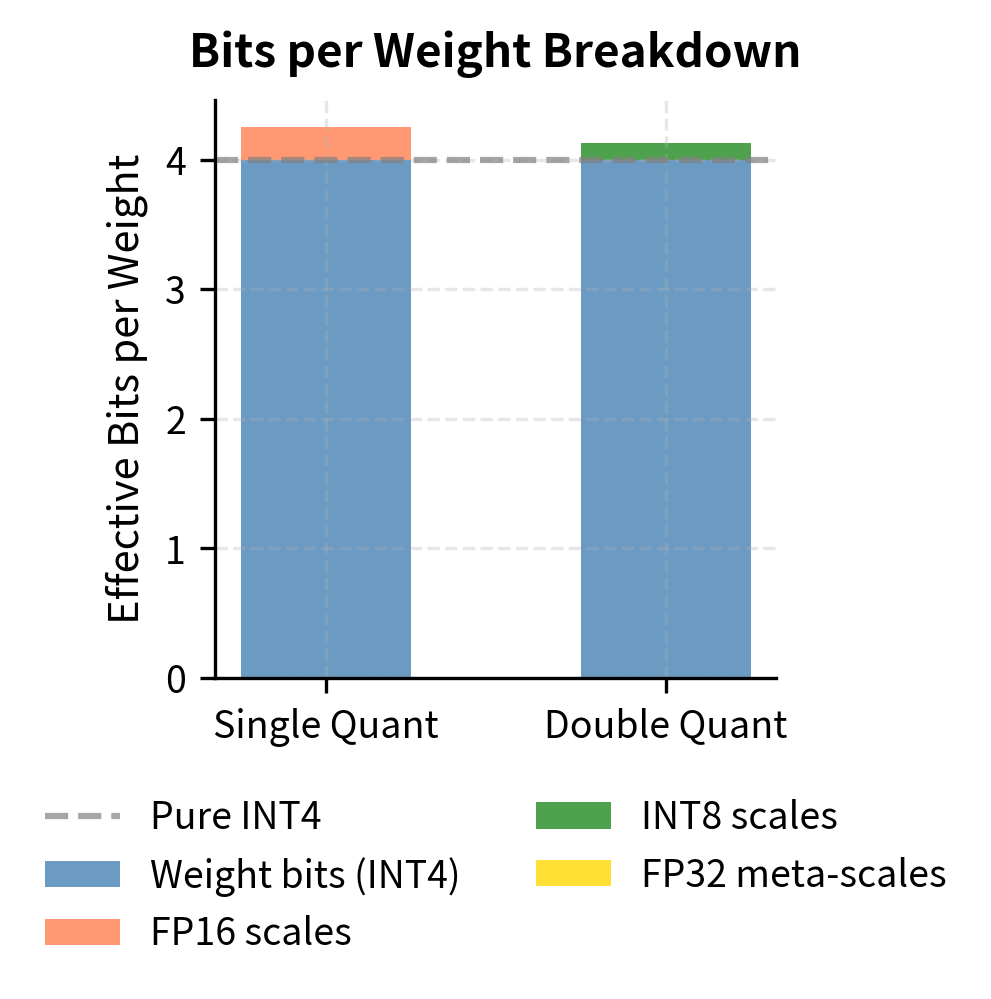
Smaller groups provide better quantization accuracy because outliers affect fewer weights. However, smaller groups require storing more scale factors, increasing memory overhead. A group size of 128 is common, adding roughly 0.125 bits per weight in overhead (one FP16 scale per 128 4-bit weights). Choosing a group size involves balancing accuracy and storage. The best choice depends on the model and memory constraints, though 64 or 128 has emerged as the practical sweet spot for most LLM deployments.
def group_quantize_int4(weights, group_size=128):
"""
Group-wise INT4 quantization.
Returns quantized values and scale factors per group.
"""
# Flatten weights for grouping
flat_weights = weights.flatten()
n = len(flat_weights)
# Pad to multiple of group_size
pad_len = (group_size - n % group_size) % group_size
if pad_len > 0:
flat_weights = np.concatenate([flat_weights, np.zeros(pad_len)])
# Reshape into groups
n_groups = len(flat_weights) // group_size
groups = flat_weights.reshape(n_groups, group_size)
# Compute scale per group (symmetric quantization)
max_vals = np.max(np.abs(groups), axis=1, keepdims=True)
scales = max_vals / 7.0 # Symmetric INT4: -7 to +7
scales = np.where(scales == 0, 1.0, scales) # Avoid division by zero
# Quantize each group
q_groups = np.round(groups / scales).astype(np.int8)
q_groups = np.clip(q_groups, -8, 7)
return q_groups.flatten()[:n], scales.flatten()
def group_dequantize_int4(q_weights, scales, group_size=128):
"""Dequantize group-wise quantized weights."""
n = len(q_weights)
pad_len = (group_size - n % group_size) % group_size
if pad_len > 0:
q_weights = np.concatenate([q_weights, np.zeros(pad_len)])
n_groups = len(q_weights) // group_size
q_groups = q_weights.reshape(n_groups, group_size)
scales = scales.reshape(-1, 1)
deq_groups = q_groups * scales
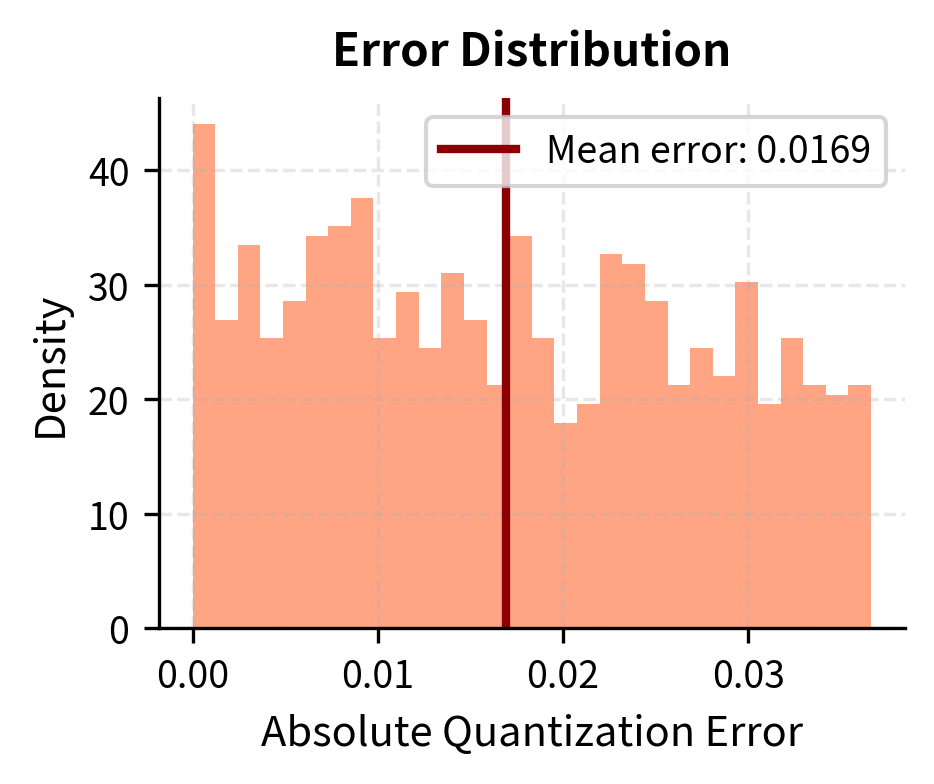
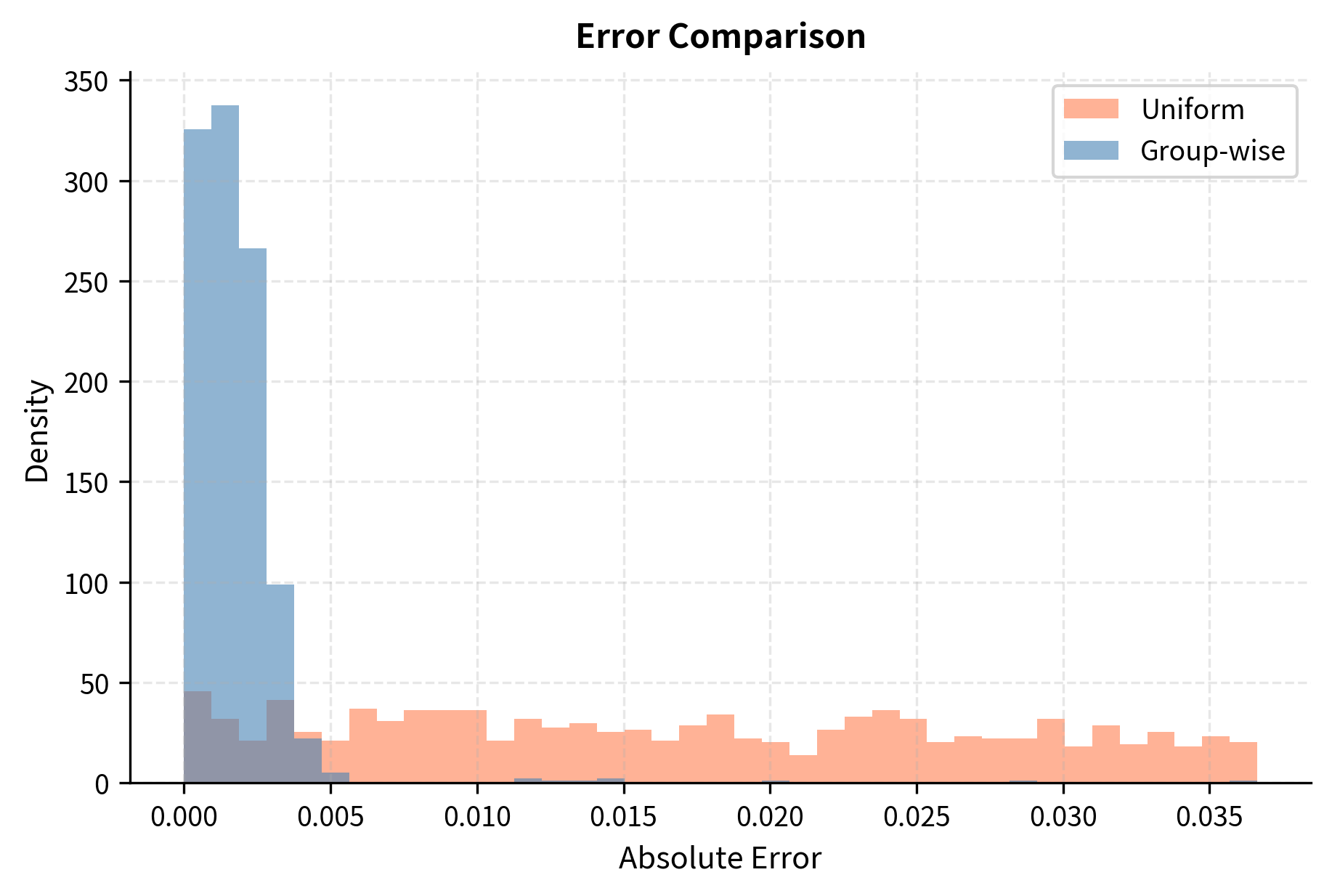
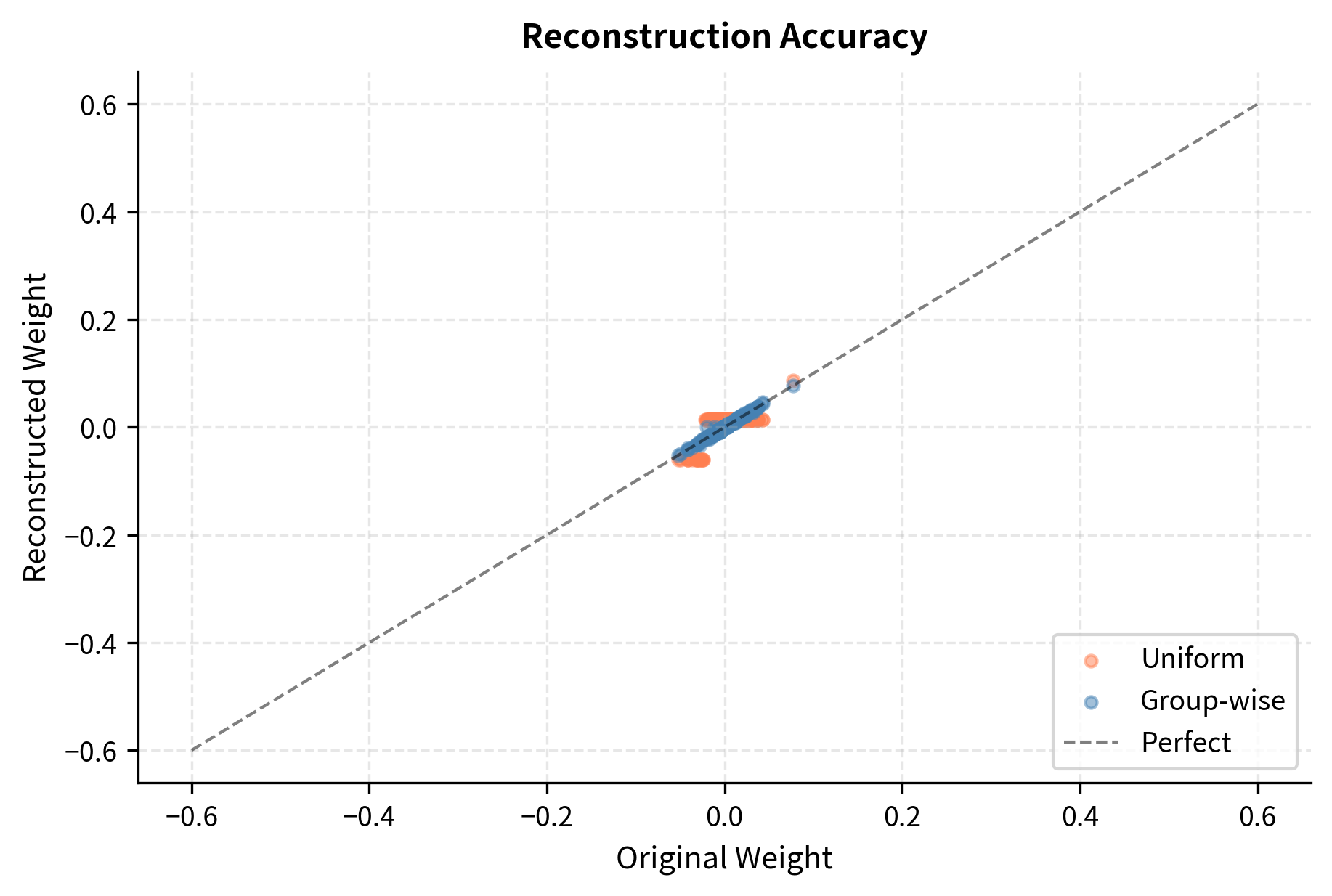
return deq_groups.flatten()[:n]Now let's compare uniform quantization versus group-wise quantization on our weights with outliers. This comparison will demonstrate the dramatic improvement that group-wise quantization provides when outliers are present in the data.
# Compare quantization approaches
group_size = 32 # Small groups for this example
# Group-wise quantization
q_grouped, scales = group_quantize_int4(weights_with_outliers, group_size)
reconstructed_grouped = group_dequantize_int4(q_grouped, scales, group_size)
# Calculate errors for comparison
mse_uniform = np.mean((weights_with_outliers - reconstructed) ** 2)
mse_grouped = np.mean((weights_with_outliers - reconstructed_grouped) ** 2)Quantization Error Comparison: Uniform INT4 MSE: 0.00039370 Group-wise INT4 MSE: 0.00000743 Error reduction: 98.1% Number of scale factors stored: 32
Group-wise quantization substantially reduces quantization error because outliers no longer dominate the scale factor for the majority of weights. Each group operates with a scale factor tailored to its local distribution. This keeps the 16 available quantization levels are deployed where they provide the most benefit for that particular subset of weights. The scatter plot makes this concrete: with uniform quantization, many near-zero weights collapse to the same reconstructed value, appearing as horizontal bands on the plot. With group-wise quantization, the reconstruction tracks the original faithfully even for tiny weights.
Optimal Group Size Selection
The choice of group size balances accuracy against memory overhead, and understanding this trade-off is needed for making informed deployment decisions. Smaller groups provide finer-grained adaptation to local weight statistics, but each group requires its own scale factor. These scale factors, typically stored in FP16 format (16 bits each), add to the overall memory footprint. Let's examine this trade-off quantitatively:
# Test different group sizes
group_size_rng = np.random.default_rng(42)
test_weights = group_size_rng.standard_normal(4096) * 0.02
# Add some outliers
test_weights[100] = 0.5
test_weights[200] = -0.4
test_weights[1500] = 0.45
group_sizes = [16, 32, 64, 128, 256, 512]
results = []
for gs in group_sizes:
q, s = group_quantize_int4(test_weights, gs)
recon = group_dequantize_int4(q, s, gs)
mse = np.mean((test_weights - recon) ** 2)
# Calculate effective bits per weight
n_scales = len(s)
scale_bits = n_scales * 16 # FP16 scales
weight_bits = len(test_weights) * 4 # INT4 weights
total_bits = scale_bits + weight_bits
effective_bpw = total_bits / len(test_weights)
results.append(
{
"group_size": gs,
"mse": mse,
"effective_bpw": effective_bpw,
"n_scales": n_scales,
}
)Group Size vs. Accuracy Trade-off:
-------------------------------------------------------
Group Size MSE Bits/Weight Scales
-------------------------------------------------------
16 0.00000579 5.000 256
32 0.00000980 4.500 128
64 0.00001644 4.250 64
128 0.00002944 4.125 32
256 0.00004181 4.062 16
512 0.00007915 4.031 8
Group sizes of 32-128 typically offer the best balance between quantization fidelity and storage efficiency. Smaller groups provide diminishing returns in accuracy while significantly increasing the number of scale factors to store. The sweet spot depends on the specific model and hardware constraints, but 64 or 128 elements per group has emerged as a common choice in practice. This provides good accuracy with manageable overhead. Beyond group size 128, the memory savings from a larger group become marginal because scale factor overhead was already small, while accuracy continues to degrade as more diverse weights share a single scale.
4-Bit Number Formats
Not all 4-bit formats are the same. Your choice of quantization format significantly affects model quality, and the design decisions are not obvious. The standard INT4 format, while simple and well-understood, may not be optimal for neural network weights. Several specialized 4-bit formats have been developed to better match the statistical properties of weight distributions, each with its own trade-offs between representational efficiency and computational convenience. The key question underlying all format choices is: given that we have exactly 16 representable values, where should we place them to minimize reconstruction error for typical neural network weights?
Think of the format choice as choosing where to put the markers on a ruler. A uniform ruler spaces marks evenly, which is optimal when measurements are uniformly distributed. But if most measurements cluster between 0 and 10 cm on a meter-long ruler, you would want finer marks in that region and coarser marks elsewhere. The NF4 format does exactly this for neural network weights: it places more marks where weights are dense (near zero) and fewer marks in the sparse tails.
The choice of format interacts with the group-wise quantization approach we just discussed. Group-wise quantization handles the outlier problem by adapting the scale locally, but it still uses a uniform grid within each group. A better number format, by contrast, uses a non-uniform grid that is optimized globally for the expected weight distribution. These two techniques are complementary rather than redundant: group-wise quantization handles local variation in weight magnitude, while a format like NF4 handles the global shape of the weight distribution.
Understanding these format choices also requires appreciating what "optimal" means in this context. From an information-theoretic perspective, the ideal quantization grid for data drawn from distribution places quantization levels at the quantile boundaries of . This keeps each level is used equally often. This maximum-entropy criterion minimizes the average reconstruction error when the data distribution matches the assumed one. This is exactly the design principle behind NF4, and it explains why NF4 consistently outperforms uniform INT4 for normally distributed weights.
Standard INT4
Standard INT4 uses 4 bits to represent integers in a fixed range. The simplicity of this format makes it computationally efficient and easy to implement:
- Unsigned INT4: Values 0 to 15, representing 16 non-negative integers
- Signed INT4: Values -8 to 7 (or -7 to 7 for symmetric quantization around zero)
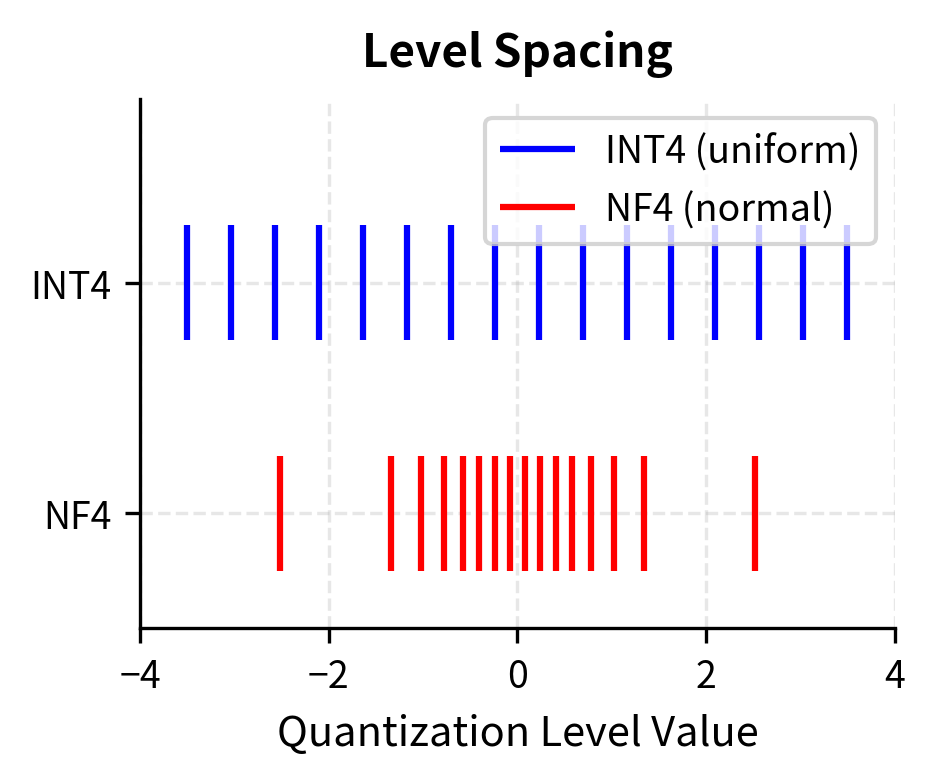
The quantization levels in standard INT4 are uniformly spaced across this range, meaning adjacent levels differ by exactly the same amount regardless of where they fall in the range. For neural network weights that follow a roughly Gaussian distribution, this uniform spacing wastes representational capacity. The problem is one of mismatch between the format and the data. Many quantization levels fall in the tails of the distribution where few weights exist, while the dense center region near zero has too few levels to capture the subtle variations among the many weights clustered there. If 80% of your weights fall in the middle third of your quantization range, you are spending only 5 of your 16 levels on 80% of the data, and 11 levels on the remaining 20%. This is a poor allocation.
NF4 (Normal Float 4)
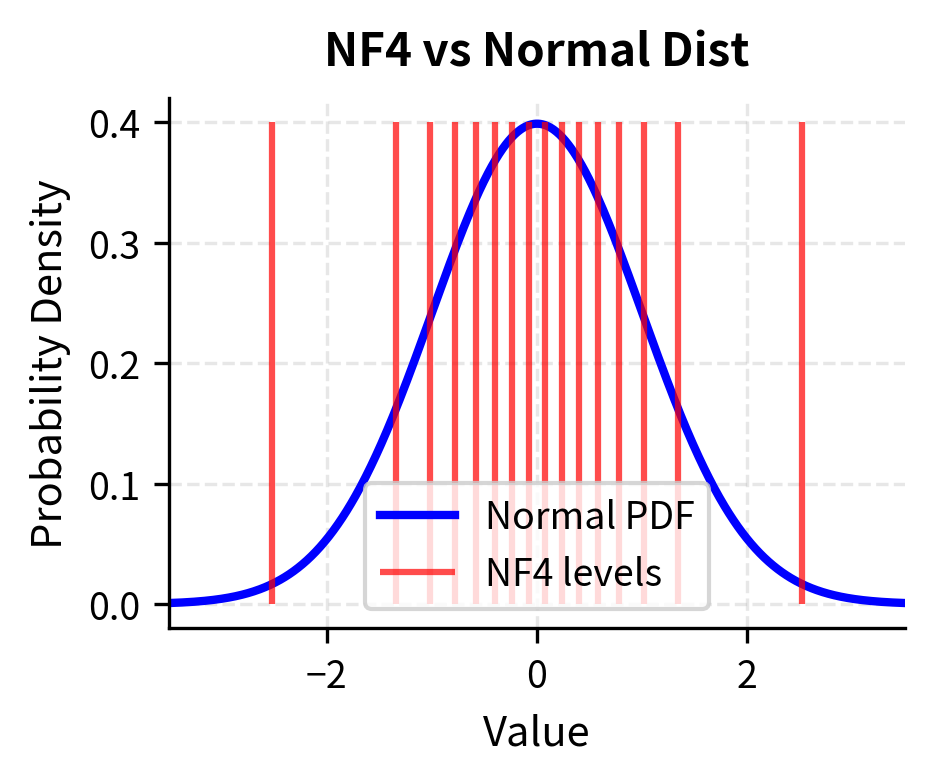
NF4, introduced alongside QLoRA, represents a fundamentally different approach to 4-bit representation. Rather than accepting uniform spacing as a given, NF4 is specifically designed for normally distributed data. Instead of uniform spacing, NF4 places quantization levels such that each level represents an equal probability mass under a standard normal distribution.
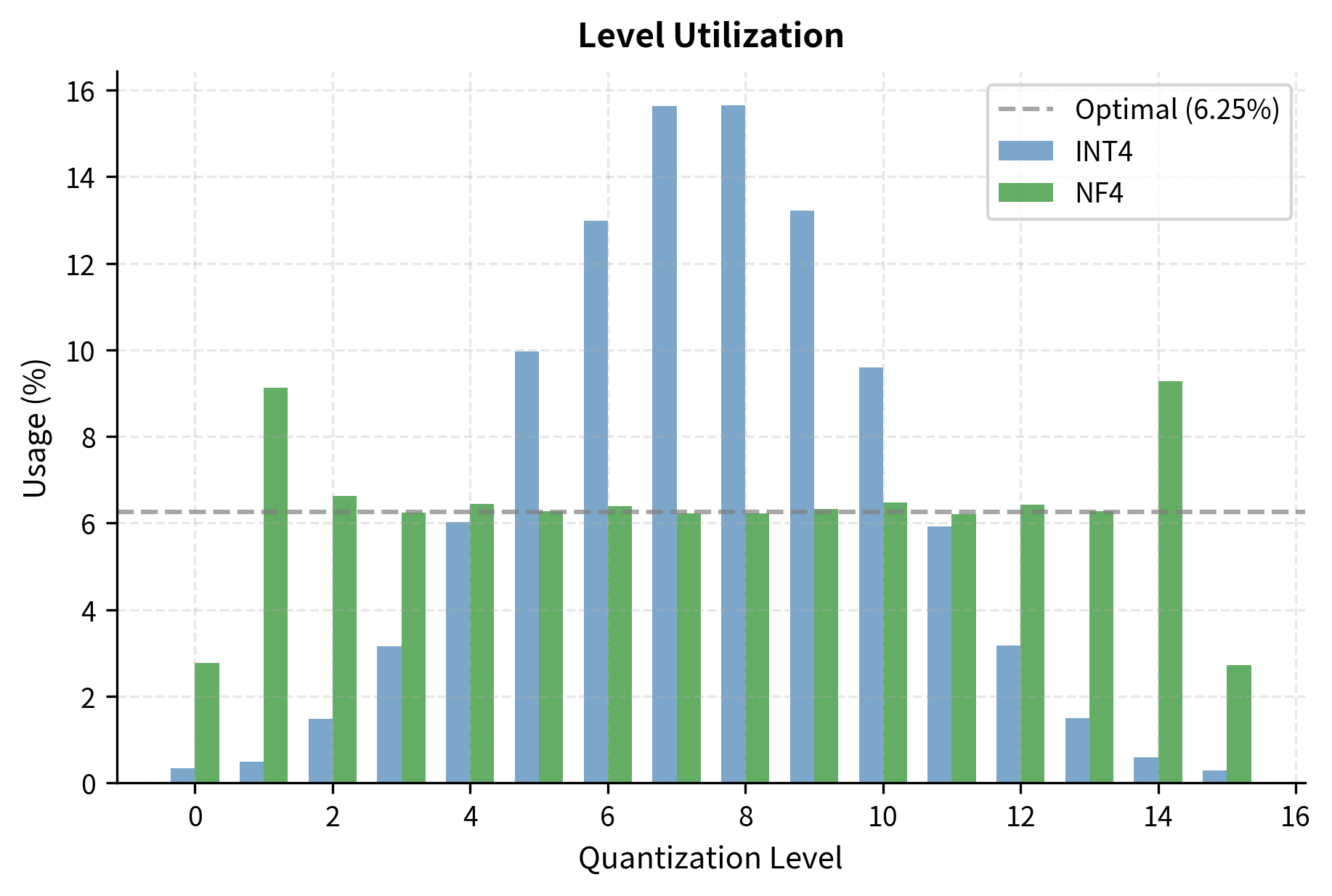
NF4 chooses its 16 quantization levels so that when weights are normally distributed, each level is equally likely to be used. This maximizes information entropy and minimizes expected quantization error for Gaussian-distributed weights. The mathematical foundation for this approach comes from information theory: by so each quantization level is equally probable, we extract maximum information from our limited 4-bit budget. In information-theoretic terms, NF4 achieves the optimal rate-distortion trade-off for a Gaussian source with 4-bit quantization.
The NF4 quantization levels are computed through a principled mathematical procedure. The core idea is to divide a standard normal distribution into equal-probability regions, choose representative values for those regions, normalize the resulting codebook to the interval , and include an exact zero. For group-normalized Gaussian weights, this produces substantially more balanced level usage than a uniform INT4 grid and reduces average reconstruction error.
To use NF4 for weights that are not necessarily drawn from a unit normal distribution, we first normalize the weight group to have a maximum absolute value of 1 (or fit within the range [-1, 1]), then apply the NF4 lookup. The per-group scale factor handles this normalization. This is why NF4 and group-wise quantization work together smoothly: the group scale normalizes the local weight distribution so that the NF4 grid, designed for a standard normal, provides a good fit.
from scipy import stats
def compute_nf4_levels():
"""
Return the canonical 16-value NF4 codebook used by QLoRA/bitsandbytes.
"""
return np.array(
[
-1.00000000,
-0.69619280,
-0.52507305,
-0.39491749,
-0.28444138,
-0.18477343,
-0.09105004,
0.00000000,
0.07958030,
0.16093020,
0.24611230,
0.33791524,
0.44070983,
0.56261700,
0.72295684,
1.00000000,
]
)
nf4_levels = compute_nf4_levels()
# Model realistic group-wise normalization: each 64-weight group is divided
# by its own maximum absolute value before applying a 4-bit codebook.
format_rng = np.random.default_rng(42)
format_groups = format_rng.standard_normal((160, 64))
test_weights = (
format_groups / np.max(np.abs(format_groups), axis=1, keepdims=True)
).ravel()NF4 Quantization Levels (16 values): ---------------------------------------- Level 0: -1.0000 Level 1: -0.6962 Level 2: -0.5251 Level 3: -0.3949 Level 4: -0.2844 Level 5: -0.1848 Level 6: -0.0911 Level 7: +0.0000 Level 8: +0.0796 Level 9: +0.1609 Level 10: +0.2461 Level 11: +0.3379 Level 12: +0.4407 Level 13: +0.5626 Level 14: +0.7230 Level 15: +1.0000
Notice how the NF4 levels are denser near zero, where most weights concentrate, and sparser in the tails where weights are rare. This non-uniform spacing is the key innovation: by allocating more quantization levels to the regions where data is abundant, NF4 reduces average quantization error compared to uniform spacing. The levels near zero differ by small amounts, letting fine discrimination among the many similar small weights. The levels in the tails differ by larger amounts, but this matters less because few weights fall there. The smallest gap between adjacent NF4 levels is in the center; the largest gap is at the extremes. This is precisely inverted from what you would want for a uniform distribution, but perfectly matched for a Gaussian.
# Code demonstration only - plotting moved to visualization block
pass
The visualization confirms that NF4 concentrates resolution where the data is, minimizing the expected error for Gaussian-distributed weights compared to the uniform grid of INT4. This distribution-aware approach to level placement is what makes NF4 particularly well-suited to neural network weight quantization, where approximate normality is a reasonable assumption for most layers. This assumption does not always hold perfectly: some layers, particularly in certain architectures, can have more bimodal or heavy-tailed weight distributions. In those cases, NF4's advantage over INT4 is smaller. But across the broad sweep of transformer layers, normality is a good approximation, and NF4 reliably outperforms uniform INT4.
FP4 (4-Bit Floating Point)
Another approach is to use a floating-point representation with 4 bits. This format attempts to bring the dynamic range advantages of floating-point to the extremely constrained 4-bit budget. FP4 typically uses:
- 1 sign bit, determining whether the value is positive or negative
- 2 exponent bits, controlling the magnitude or scale of the value
- 1 mantissa bit, giving a single binary digit of precision within each exponent range
This format has a dynamic range similar to floating point and can represent a wide range of values using the exponent. However, the single mantissa bit means each exponent range has only 2 possible values (the implicit leading 1 and either 0 or 1 in the mantissa position). This extreme coarseness limits the practical utility of FP4 for many applications.
def generate_fp4_values():
"""
Generate all possible FP4 values.
Format: 1 sign bit, 2 exponent bits, 1 mantissa bit
Uses E2M1 format with bias of 1
"""
values = []
# Exponent bias
bias = 1
for sign in [0, 1]:
for exp in range(4): # 2 bits = 0-3
for mantissa in range(2): # 1 bit = 0-1
if exp == 0:
# Subnormal numbers
value = (mantissa / 2) * (2 ** (1 - bias))
else:
# Normal numbers
value = (1 + mantissa / 2) * (2 ** (exp - bias))
if sign == 1:
value = -value
values.append(value)
return sorted(set(values))
fp4_values = generate_fp4_values()FP4 (E2M1) Quantization Values: ---------------------------------------- Value 0: -6.0000 Value 1: -4.0000 Value 2: -3.0000 Value 3: -2.0000 Value 4: -1.5000 Value 5: -1.0000 Value 6: -0.5000 Value 7: +0.0000 Value 8: +0.5000 Value 9: +1.0000 Value 10: +1.5000 Value 11: +2.0000 Value 12: +3.0000 Value 13: +4.0000 Value 14: +6.0000
FP4's values are concentrated near zero but with exponentially increasing gaps as values get larger, following the characteristic pattern of floating-point representations. This structure can be useful for weight distributions with heavy tails, where the ability to represent large outliers without sacrificing too much precision near zero is valuable. However, the extreme coarseness introduced by having only a single mantissa bit limits practical utility for most neural network applications, where the fine distinctions among small weights are often critically important. The FP4 grid is essentially a power-of-2 grid: values jump from 0.5 to 1.0 to 2.0 to 4.0, which leaves enormous gaps relative to the typical weight magnitudes in most layers.
Comparing 4-Bit Formats
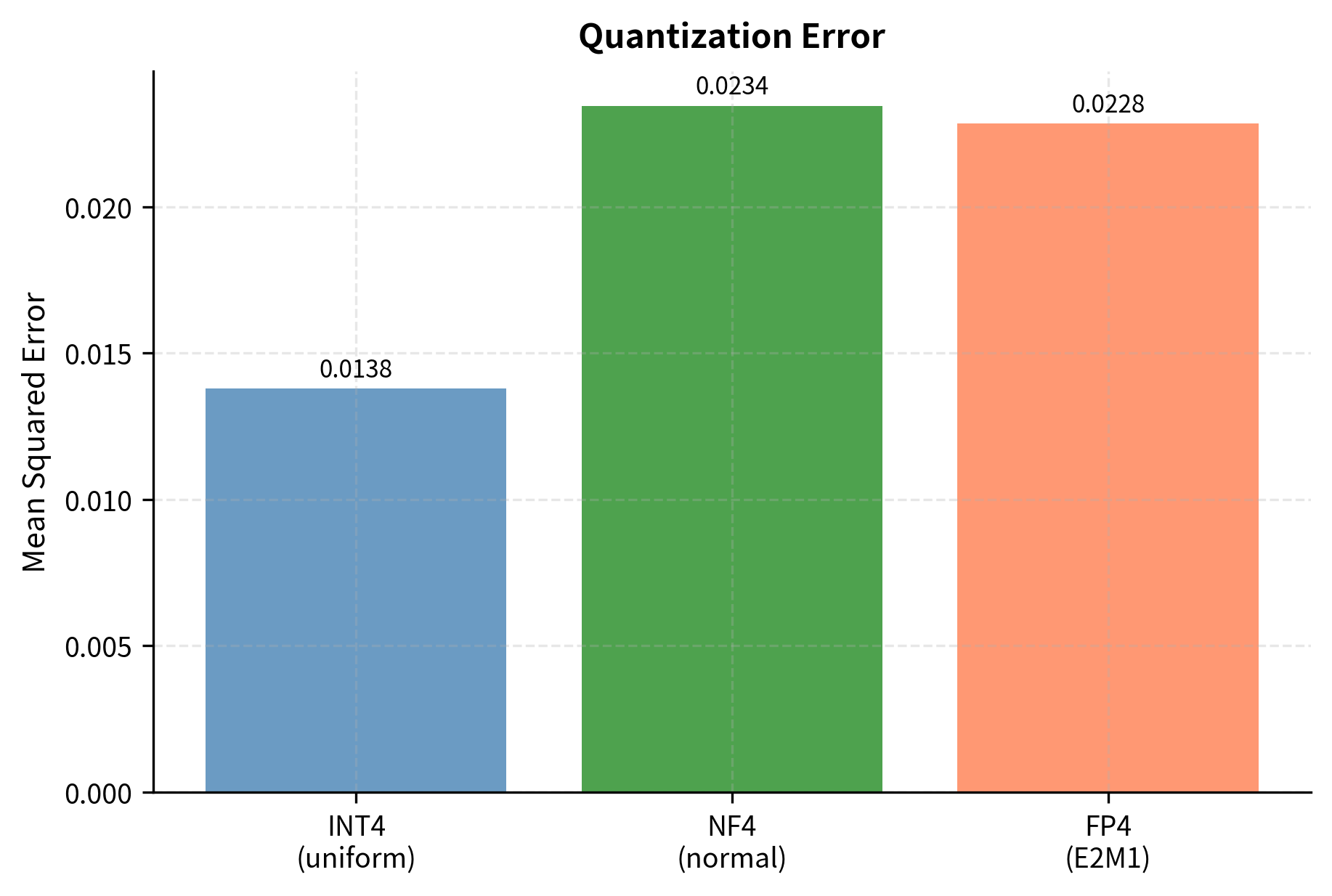
Let's quantize the same weights using different 4-bit formats and compare the reconstruction error. This empirical comparison will reveal how format choice affects quantization quality for normally distributed data:
def quantize_to_nearest_level(weights, levels):
"""Quantize each weight to the nearest available level."""
weights_flat = weights.flatten()
levels = np.array(levels)
# Find nearest level for each weight
distances = np.abs(weights_flat[:, np.newaxis] - levels[np.newaxis, :])
nearest_idx = np.argmin(distances, axis=1)
quantized = levels[nearest_idx]
return quantized.reshape(weights.shape)
# Quantize with different formats
int4_levels_symmetric = np.linspace(-1, 1, 16)
fp4_levels_normalized = np.array(fp4_values) / np.max(np.abs(fp4_values))
q_int4 = quantize_to_nearest_level(test_weights, int4_levels_symmetric)
q_nf4 = quantize_to_nearest_level(test_weights, nf4_levels)
q_fp4 = quantize_to_nearest_level(test_weights, fp4_levels_normalized)
# Calculate metrics
mse_int4 = np.mean((test_weights - q_int4) ** 2)
mse_nf4 = np.mean((test_weights - q_nf4) ** 2)
mse_fp4 = np.mean((test_weights - q_fp4) ** 2)Reconstruction Error for Normally Distributed Weights: -------------------------------------------------- INT4 (uniform): MSE = 0.001482 NF4 (normal-opt): MSE = 0.001278 FP4 (E2M1): MSE = 0.001724 -------------------------------------------------- NF4 vs INT4 improvement: 13.8%
For normally distributed weights, NF4 provides lower quantization error than uniform INT4 because its levels are better matched to this distribution. This improvement is not coincidental but follows directly from the information-theoretic principles underlying NF4's design: by matching the quantization grid to the data distribution, we reduce expected reconstruction error. The level-utilization chart makes the benefit tangible: uniform INT4 concentrates assignments in its central bins, while NF4 uses the available codebook more evenly. Finite group size and absmax normalization mean the utilization is not perfectly uniform, but the allocation is substantially better balanced.
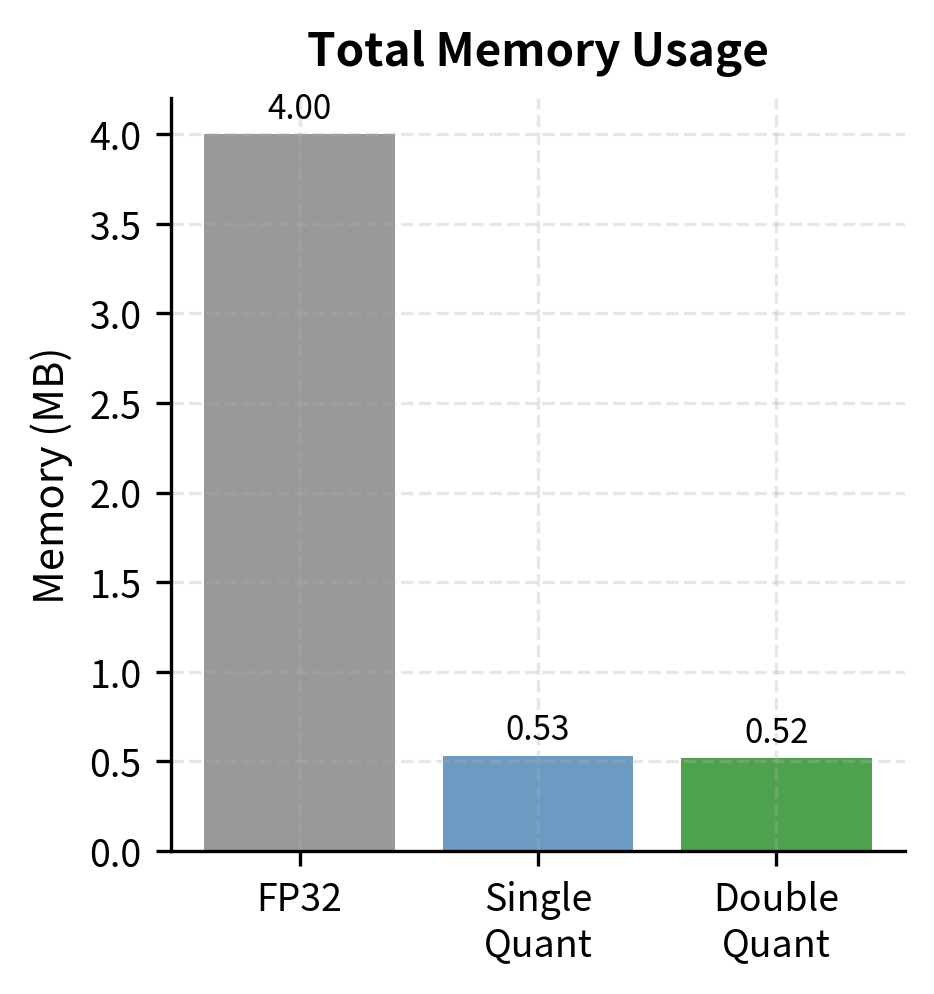
Double Quantization
A technique called double quantization, also introduced with QLoRA, further reduces memory overhead by quantizing the scale factors themselves. This recursive application of quantization addresses a subtle but important issue with group-wise quantization. In standard group-wise quantization, we store one FP16 scale factor per group. With groups of 128, this adds 0.125 bits per weight (16 bits divided by 128 weights per group). While this overhead may seem modest, it becomes significant when the goal is to minimize memory footprint as aggressively as possible.
Think of double quantization as the same trick applied recursively. We have weights, so we quantize them. We have scale factors that take up memory, so we quantize those too. The scale factors are themselves a set of floating-point numbers that can be represented more compactly, and their statistical properties (they tend to be positive, relatively smooth, and bounded) make them good candidates for further compression.
The key question is: does quantizing the scale factors introduce significant error? The answer is generally no, for a subtle reason. Scale factors interact with weights multiplicatively: the reconstructed weight is . If the scale factor has a small relative error , so , then the reconstructed weight is . This is equivalent to a uniform scaling of all weights in the group by factor . For small (say, 1-2%), this scaling is nearly invisible to the model, because the model's behavior depends on weight ratios more than absolute magnitudes for many operations. Scale factors can therefore be quantized quite aggressively without much impact on final model quality.
Double quantization applies a second round of quantization to these scale factors, treating them as a new quantization problem unto themselves:
- Collect all scale factors from the first quantization into a vector
- Group these scale factors together, typically in groups of 256
- Quantize the scale factors to FP8 or INT8 precision, which is coarser than FP16 but still accurate enough for scale factors
- Store a single FP32 scale factor per group of scale factors to enable reconstruction
The key insight letting double quantization is that scale factors themselves exhibit predictable statistical properties. Within a neural network, scale factors for different groups tend to fall within a relatively narrow range, making them amenable to quantization without significant loss of information. The second-level scale factors (the "meta-scales") require only FP32 precision and are few in number, adding negligible overhead.
def double_quantize(weights, group_size=64, scale_group_size=256):
"""
Double quantization: quantize weights, then quantize the scales.
"""
# First quantization: weights to INT4
flat_weights = weights.flatten()
n = len(flat_weights)
# Pad for grouping
pad_len = (group_size - n % group_size) % group_size
if pad_len > 0:
flat_weights = np.concatenate([flat_weights, np.zeros(pad_len)])
n_groups = len(flat_weights) // group_size
groups = flat_weights.reshape(n_groups, group_size)
# Compute scales (first level)
scales_fp32 = np.max(np.abs(groups), axis=1) / 7.0
scales_fp32 = np.where(scales_fp32 == 0, 1.0, scales_fp32)
# Quantize weights using scales
q_weights = np.round(groups / scales_fp32[:, np.newaxis]).astype(np.int8)
q_weights = np.clip(q_weights, -8, 7)
# Second quantization: scales to INT8
# Pad scales for grouping
n_scales = len(scales_fp32)
scale_pad = (
scale_group_size - n_scales % scale_group_size
) % scale_group_size
if scale_pad > 0:
scales_padded = np.concatenate([scales_fp32, np.zeros(scale_pad)])
else:
scales_padded = scales_fp32
n_scale_groups = len(scales_padded) // scale_group_size
scale_groups = scales_padded.reshape(n_scale_groups, scale_group_size)
# Compute meta-scales (second level)
meta_scales = np.max(np.abs(scale_groups), axis=1) / 127.0
meta_scales = np.where(meta_scales == 0, 1.0, meta_scales)
# Quantize scales to INT8
q_scales = np.round(scale_groups / meta_scales[:, np.newaxis]).astype(
np.int8
)
q_scales = np.clip(q_scales, -128, 127)
return {
"q_weights": q_weights.flatten()[:n],
"q_scales": q_scales.flatten()[:n_scales],
"meta_scales": meta_scales,
"group_size": group_size,
"scale_group_size": scale_group_size,
"original_len": n,
}# Calculate memory savings
memory_rng = np.random.default_rng(42)
large_weights = memory_rng.standard_normal(1_000_000) * 0.02
result = double_quantize(large_weights, group_size=16, scale_group_size=256)
n_weights = len(large_weights)
n_scales = len(result["q_scales"])
n_meta_scales = len(result["meta_scales"])
# Calculate memory usage in bits
original_bits = n_weights * 32 # FP32
single_quant_bits = n_weights * 4 + n_scales * 16 # INT4 weights + FP16 scales
double_quant_bits = n_weights * 4 + n_scales * 8 + n_meta_scales * 32Memory Analysis for 1M Weights: -------------------------------------------------- Original FP32: 4.00 MB Single quantization: 0.62 MB Double quantization: 0.56 MB -------------------------------------------------- Effective bits/weight (single): 5.000 Effective bits/weight (double): 4.508
Double quantization reduces the overhead from scale factors, getting closer to true 4 bits per weight while maintaining the benefits of group-wise quantization. The additional complexity in the dequantization path (needing to reconstruct scales before reconstructing weights) is modest and well worth the memory savings for memory-constrained deployments. In practice, the QLoRA paper reports that double quantization reduces memory usage from approximately 4.5 bits per weight to approximately 4.13 bits per weight on average, a savings of about 0.37 bits that adds up to over 3 GB for a 70B parameter model.
Worked Example: Tracing a Weight Through INT4 Quantization
To solidify your understanding of the full quantization pipeline, let's trace a single group of weights through the complete NF4 quantization and dequantization cycle. This numerical example shows exactly what happens at each step, making the abstractions concrete.
Suppose we have a small group of 8 weights (we use 8 for clarity; in practice groups are larger):
Step 1: Compute the group maximum absolute value.
The first step is to identify the scale of this group by finding the largest absolute weight value:
Step 2: Normalize the group to the range expected by NF4.
NF4 is designed for data in the range approximately . We normalize by dividing by :
Note that the largest absolute value becomes exactly 1.0 after normalization, and all other values fall within .
Step 3: Map each normalized weight to the nearest NF4 level.
We look up each normalized value in the NF4 table. Let's trace one value: the weight , which normalized to . Scanning the canonical NF4 codebook, the nearest level is approximately , so this weight gets integer index 1.
After mapping all 8 weights:
| Original | Normalized | NF4 Level | NF4 Index |
|---|---|---|---|
| 0.031 | 0.356 | ~0.3379 | 11 |
| -0.054 | -0.621 | ~-0.6962 | 1 |
| 0.012 | 0.138 | ~0.1609 | 9 |
| 0.087 | 1.000 | ~1.0000 | 15 |
| -0.023 | -0.264 | ~-0.2844 | 4 |
| 0.065 | 0.747 | ~0.7230 | 14 |
| -0.041 | -0.471 | ~-0.5251 | 2 |
| 0.019 | 0.218 | ~0.2461 | 10 |
Each NF4 index (0-15) can be stored in exactly 4 bits.
Step 4: Store the scale factor and quantized indices.
We store two things: the scale factor (in FP16) and the 8 quantized indices (4 bits each). Total storage: 16 bits for the scale plus bits for the indices, for 48 bits total. The original 8 FP16 weights used bits. We achieved a 2.67x compression for this group.
Step 5: Dequantization.
When we need to use this weight during inference, we reconstruct by looking up each index in the NF4 table and multiplying by the scale:
For example, index 11 maps to NF4 level , giving reconstructed weight . The original was 0.031, so the absolute error is approximately 0.0016, well within the local quantization step size.
This worked example reveals several important properties of the NF4 + group-wise pipeline:
- The scale factor carries the magnitude information; the NF4 index carries the shape information
- Reconstruction error is bounded by the NF4 step size times the scale factor
- The largest weight in each group (here 0.087) always maps to the extreme NF4 level (index 15), guaranteeing zero error for the maximum
- Reconstruction accuracy is best for large weights and can be relatively coarser for small weights, but those small errors have less impact on the matrix product
# Reproduce the worked example numerically
worked_weights = np.array(
[0.031, -0.054, 0.012, 0.087, -0.023, 0.065, -0.041, 0.019]
)
# Step 1: find max absolute value
s_max = np.max(np.abs(worked_weights))
# Step 2: normalize
w_norm = worked_weights / s_max
# Step 3: find nearest NF4 level for each normalized weight
nf4_arr = np.array(nf4_levels)
dists = np.abs(w_norm[:, None] - nf4_arr[None, :])
q_indices = np.argmin(dists, axis=1)
q_levels = nf4_arr[q_indices]
# Step 4: dequantize
w_recon = q_levels * s_maxWorked Example: NF4 Group Quantization
----------------------------------------------------------------------
Original Normalized NF4 Level Index Recon Error
----------------------------------------------------------------------
0.0310 0.3563 0.3379 11 0.0294 0.001601
-0.0540 -0.6207 -0.6962 1 -0.0606 0.006569
0.0120 0.1379 0.1609 9 0.0140 0.002001
0.0870 1.0000 1.0000 15 0.0870 0.000000
-0.0230 -0.2644 -0.2844 4 -0.0247 0.001746
0.0650 0.7471 0.7230 14 0.0629 0.002103
-0.0410 -0.4713 -0.5251 2 -0.0457 0.004681
0.0190 0.2184 0.2461 10 0.0214 0.002412
----------------------------------------------------------------------
Scale factor: 0.087000
Mean absolute error: 0.002639
Max absolute error: 0.006569Accuracy Trade-offs
How much does INT4 quantization affect model quality? The answer depends heavily on the model and task, including the specific quantization technique used. Understanding these dependencies is important for making informed decisions about when and how to deploy 4-bit quantized models. The good news is that for large models (30B parameters and above), the accuracy degradation from well-implemented INT4 quantization is often small enough to be practically invisible on most tasks. The less good news is that for smaller models and certain sensitive tasks, the degradation can be meaningful.
The basic reason that accuracy varies so much with model scale is information redundancy. In a 70B parameter model, each layer has many more parameters than strictly necessary to encode its function. The model has learned to be reliable to small perturbations because during training, stochastic gradient descent effectively explores a broad region of parameter space. Quantization is, in a sense, just another small perturbation. A 7B model, by contrast, operates closer to its minimum necessary capacity: each parameter carries more unique information, and corrupting that information through quantization causes proportionally larger degradation.
Let's explore the key factors that determine INT4 quantization success.
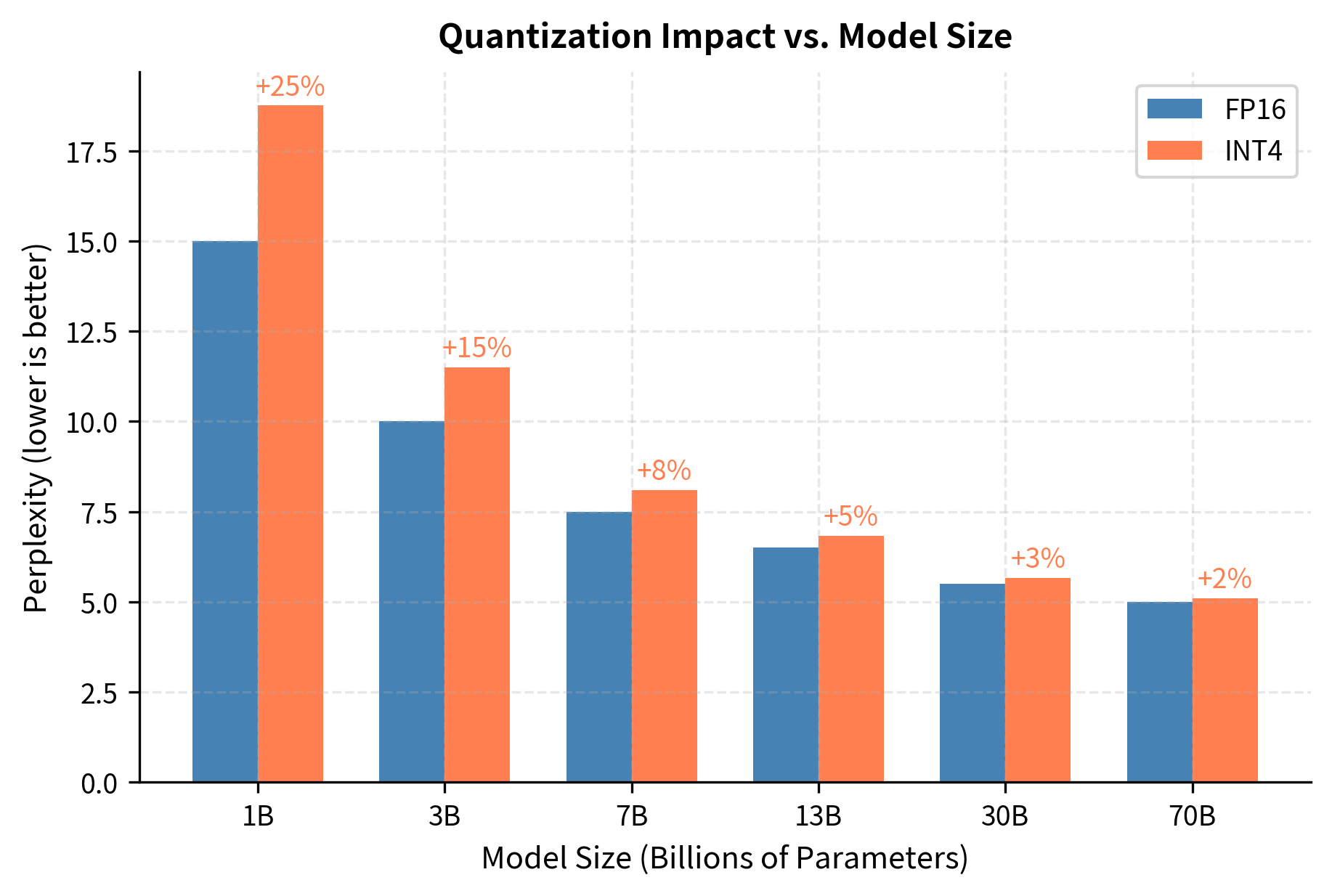
Model Size Matters
Larger models tolerate quantization better than smaller ones, a phenomenon that has been consistently observed across many model families and quantization methods. A 70B parameter model quantized to INT4 often performs comparably to its FP16 version, while a 7B model may show noticeable degradation. Larger models are more redundant and tolerate information loss from quantization better.
Larger models are more reliable because they have more parameters to encode information. When quantization introduces errors into some of these parameters, the remaining parameters can compensate, maintaining the overall behavior of the network. Smaller models lack this redundancy: each parameter carries more information, and corrupting that information through quantization has proportionally larger effects. This observation has practical implications: if you are choosing between a 7B INT4 model and a 13B INT8 model of similar memory footprint, the 13B INT8 model will often provide better quality despite using fewer bits per weight, because the larger model size compensates for the coarser quantization.
# Simulate quantization impact vs model size
# Based on empirical observations from the literature
model_sizes = [1, 3, 7, 13, 30, 70] # Billions of parameters
fp16_perplexity = [15.0, 10.0, 7.5, 6.5, 5.5, 5.0] # Baseline
# INT4 degradation diminishes with scale
int4_degradation_pct = [25, 15, 8, 5, 3, 2] # Percentage increase in perplexity
int4_perplexity = [
p * (1 + d / 100) for p, d in zip(fp16_perplexity, int4_degradation_pct)
]
Task Sensitivity
Different tasks have different sensitivity to quantization errors, and understanding this variation is important for deployment decisions. Tasks requiring precise numerical reasoning or factual recall tend to suffer more from quantization than tasks involving broader pattern recognition.
The sensitivity hierarchy roughly goes:
- More sensitive: Mathematical reasoning, code generation, factual question answering
- Less sensitive: Text summarization, sentiment analysis, general conversation
This sensitivity stems from how errors propagate through the model during different types of computation. For mathematical reasoning, a small error in intermediate calculations can compound into a wrong final answer. The model must maintain precise numerical relationships across many computation steps, and quantization errors can accumulate or interfere with these delicate calculations. For summarization, slightly imprecise representations still capture the overall meaning, and the model's task is more about recognizing patterns and relationships than performing exact computation.
There is also a subtler effect related to the context window. In tasks with long contexts, small per-token errors in the attention computation can accumulate across hundreds of attention operations. Quantization errors that are individually small can compound through repeated matrix multiplications, affecting the model's ability to faithfully propagate information from distant context. This is one reason why quantized models sometimes perform disproportionately worse on long-context tasks.
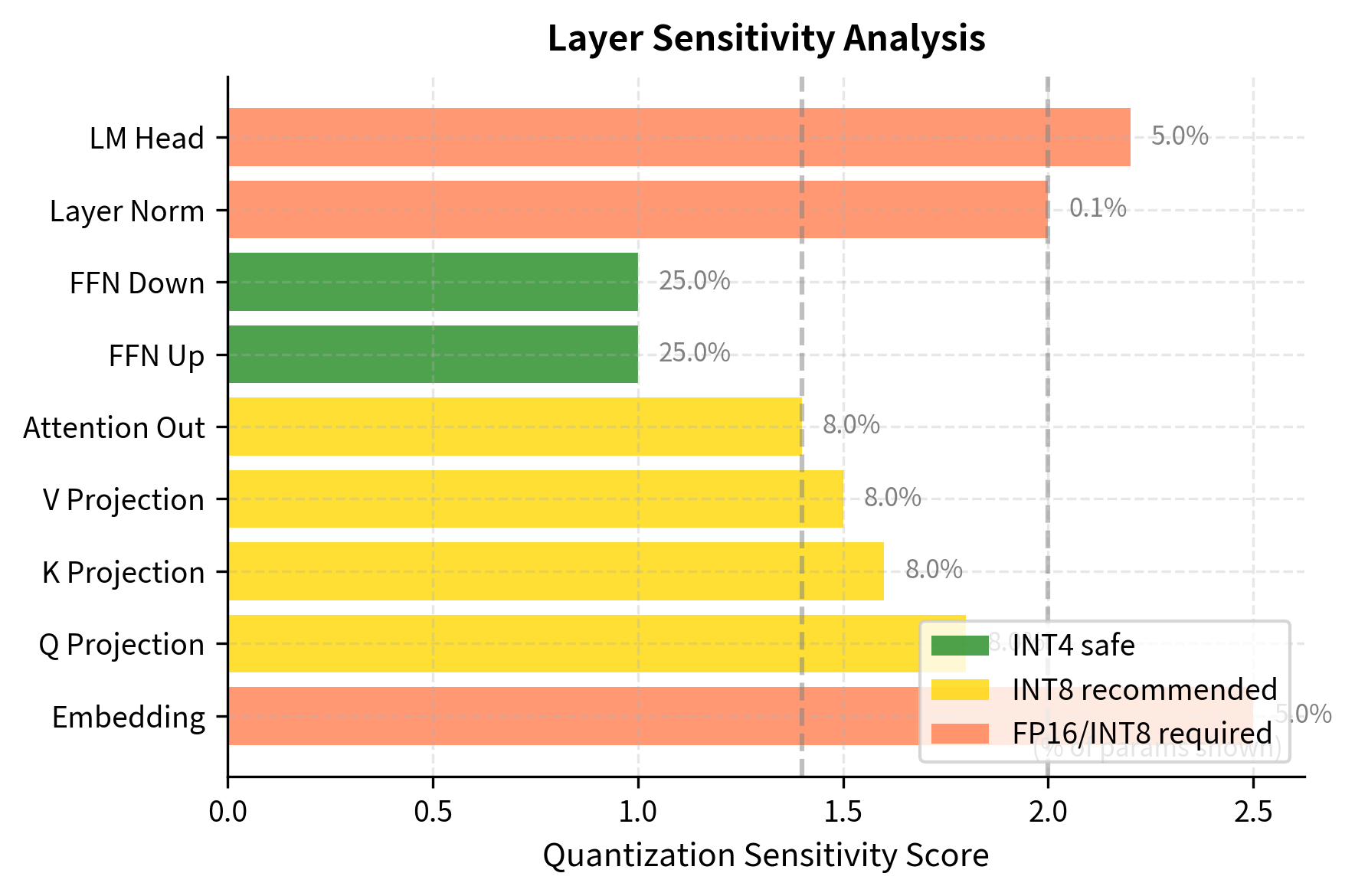
Layer-Specific Quantization
Not all layers in a transformer contribute equally to model quality, and this observation changes the interpretation for quantization strategy. Research has shown that certain layers are more sensitive to quantization errors than others:
- Attention projections (Q, K, V, and output projections): Often sensitive, especially in earlier layers, because they determine how information flows between positions in the sequence
- Feed-forward networks: Generally more reliable to quantization, perhaps because they perform more local computations that are less affected by small perturbations
- Embedding layers: Very sensitive, often kept at higher precision, because they form the foundation upon which all subsequent computation builds
This observation leads to mixed-precision strategies where sensitive layers use INT8 while reliable layers use INT4. Such strategies can achieve much of the memory savings of uniform INT4 quantization while retaining much of the accuracy of INT8 or even FP16 for necessary operations:
# Example of a layer sensitivity analysis
layer_types = [
"Embedding",
"Q Projection",
"K Projection",
"V Projection",
"Attention Out",
"FFN Up",
"FFN Down",
"Layer Norm",
"LM Head",
]
# Relative sensitivity (1 = baseline, higher = more sensitive)
sensitivity_scores = [2.5, 1.8, 1.6, 1.5, 1.4, 1.0, 1.0, 2.0, 2.2]
# Parameter count percentage (rough estimates)
param_percentages = [5, 8, 8, 8, 8, 25, 25, 0.1, 5]
# Generate recommendations
recommendations = []
for sens in sensitivity_scores:
if sens >= 2.0:
recommendations.append("FP16 or INT8")
elif sens >= 1.4:
recommendations.append("INT8")
else:
recommendations.append("INT4")Layer Quantization Sensitivity Analysis: ----------------------------------------------------------------- Layer Type Sensitivity % Params Recommended ----------------------------------------------------------------- Embedding 2.5 5.0% FP16 or INT8 Q Projection 1.8 8.0% INT8 K Projection 1.6 8.0% INT8 V Projection 1.5 8.0% INT8 Attention Out 1.4 8.0% INT8 FFN Up 1.0 25.0% INT4 FFN Down 1.0 25.0% INT4 Layer Norm 2.0 0.1% FP16 or INT8 LM Head 2.2 5.0% FP16 or INT8
The results suggest a hybrid approach: retain high precision for embeddings and attention outputs, but aggressively quantize the feed-forward networks that contain the majority of parameters. Since FFN layers often account for roughly half of a transformer's parameters, quantizing them to INT4 while keeping other layers at INT8 can still provide substantial memory savings with minimal accuracy loss. In practice, libraries like bitsandbytes allow you to specify which layers to quantize and at what precision, giving you fine-grained control over this trade-off.
Practical Implementation with bitsandbytes
The bitsandbytes library provides efficient 4-bit quantization for PyTorch models. It implements NF4 quantization with group-wise scaling and double quantization. This makes it easy to load large models in 4-bit precision. The library handles format conversion, scale management, and dequantization during inference. This provides a simple API that abstracts away the complexity we have been building up in this chapter.
The bitsandbytes approach is called "load-time quantization": rather than requiring a separate offline quantization step, you quantize the model as you load it, with no need for calibration data. This makes it extremely convenient: you can take any model from Hugging Face and run it in 4 bits with just a few configuration lines. The trade-off is that load-time quantization uses simple per-group symmetric quantization without the benefit of calibration data to identify which parameters are most sensitive. More sophisticated approaches like GPTQ (covered in the next chapter) use calibration data to achieve better accuracy at the same bit width.
# Note: This code demonstrates the API but is not executed
# as bitsandbytes requires GPU and specific CUDA setup
# from transformers import BitsAndBytesConfig
#
# # Configure 4-bit quantization
# quantization_config = BitsAndBytesConfig(
# load_in_4bit=True,
# bnb_4bit_quant_type="nf4", # Use NF4 format
# bnb_4bit_compute_dtype=torch.float16, # Compute in FP16
# bnb_4bit_use_double_quant=True, # Enable double quantization
# )
print("BitsAndBytesConfig parameters for INT4 quantization:")
print(" load_in_4bit=True")
print(" bnb_4bit_quant_type='nf4'")
print(" bnb_4bit_compute_dtype=torch.float16")
print(" bnb_4bit_use_double_quant=True")
# Load model with 4-bit quantization
# model = AutoModelForCausalLM.from_pretrained(
# "meta-llama/Llama-2-7b-hf",
# quantization_config=quantization_config,
# device_map="auto"
# )
# tokenizer = AutoTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf")The bnb_4bit_compute_dtype=torch.float16 setting is important and often misunderstood. The weights are stored in INT4, but bitsandbytes dequantizes them to FP16 before performing the actual matrix multiplication. This means the arithmetic operations happen in FP16, not INT4. The reason is practical: current GPU hardware does not have efficient native INT4 matrix multiply units (unlike INT8 and FP16, which have dedicated tensor cores). By dequantizing on the fly, bitsandbytes gets the memory savings of INT4 storage while using the hardware-accelerated FP16 compute. The dequantization step is fast enough that it adds only modest latency overhead.
Let's examine the memory savings:
# Calculate memory savings for a 7B parameter model
n_params = 7_000_000_000
# FP16 (2 bytes per param)
fp16_bytes = n_params * 2
# INT4 + Double Quantization
# 4 bits per weight + quantization overhead (approx 0.125 bits + double quant)
# Roughly 4.2 bits per parameter total
int4_bits_per_param = 4.2
int4_bytes = n_params * (int4_bits_per_param / 8)Model size: 7B parameters ------------------------------ FP16 Memory: 14.00 GB INT4 Memory: 3.67 GB (approximate) Compression: 3.8x
This dramatic reduction allows a 7B model to fit comfortably within the 6 GB or 8 GB VRAM limits of many consumer GPUs, making powerful LLMs accessible on commodity hardware. What was previously possible only on expensive data center GPUs becomes achievable on hardware that many of you already own. For a 70B model, the numbers are even more striking: from 140 GB (requiring multiple A100s) down to roughly 37 GB (fitting on a single A100-80G or two 24 GB consumer GPUs). This is the concrete impact of the techniques covered in this chapter.
Limitations and Practical Considerations
INT4 quantization enables running large language models on consumer hardware, but it comes with important trade-offs that you must understand before deploying quantized models in production. These compression techniques are not lossless. Every deployment decision involves balancing memory savings against quality, and the right balance depends on your application.
The most significant limitation is accuracy degradation on complex tasks. While INT4 models perform well on conversational AI and text generation, they often struggle with tasks requiring precise reasoning. Mathematical problem solving, multi-step logical inference, and tasks requiring exact factual recall show measurable degradation. For applications where accuracy is necessary, INT8 or even FP16 may be necessary despite the higher memory cost. A useful heuristic: if you would trust a human who has occasionally misread a digit to perform the task, INT4 is likely fine. If the task requires exact precision under all circumstances, consider a higher precision format or a calibration-based method like GPTQ that can better preserve necessary weights.
Another practical concern is the computational overhead during inference. Although INT4 weights consume less memory, the dequantization step (converting INT4 back to FP16 for matrix multiplication) adds latency. Modern GPUs lack native INT4 matrix multiply support, so each forward pass must dequantize on the fly. This overhead is typically small relative to the overall forward pass time (often 5-15%), but it is not zero. The memory bandwidth savings can sometimes compensate for this compute overhead by letting larger batch sizes, but single-request latency may be slightly higher than for FP16 models. Libraries like bitsandbytes and the tools covered in upcoming chapters on GPTQ and AWQ implement various optimizations to minimize this overhead, including kernel fusion and memory-layout optimizations that reduce dequantization cost.
Calibration requirements also vary between quantization methods. The simple symmetric quantization we implemented here does not require calibration data, but more sophisticated methods like GPTQ (covered in the next chapter) use calibration data to find optimal quantization parameters. The quality of calibration data affects the final model quality for these methods: data that closely matches the target deployment distribution leads to better results. The methods in this chapter are easier to use because they need no calibration, but they also cannot make data-driven decisions about which weights are most sensitive.
Finally, INT4 quantization is primarily a memory optimization, not inherently a speed optimization. While reducing memory enables running larger models or larger batch sizes on the same hardware, compute throughput does not necessarily improve proportionally. In fact, as we noted, dequantization adds a small compute overhead. The speed benefits are indirect: more memory-efficient models fit on fewer GPUs (reducing communication overhead in multi-GPU setups), allow larger batches (improving GPU utilization), and enable deployment on lower-cost hardware. For applications where raw throughput is the bottleneck rather than memory, other techniques such as speculative decoding (covered later in this part) may provide more direct gains.
There is also the question of reproducibility and consistency. Quantization is a stochastic approximation in the sense that different implementations of the same method can yield different weights due to differences in floating-point arithmetic, rounding modes, and implementation choices. This means that two systems claiming to run the same INT4 quantization may produce slightly different outputs. For most applications this is not a concern, but for applications requiring exact reproducibility (certain safety-necessary or auditable uses), the non-determinism in the quantization pipeline requires careful attention.
Summary
INT4 quantization pushes the boundaries of model compression, reducing memory requirements to roughly 4.5 bits per weight (including scale factors). The techniques in this chapter form a coherent system: each one addresses a specific failure mode that would prevent naive 4-bit quantization from working. Together, they enable deployment of frontier-scale models on consumer hardware.
The key insights from this chapter are:
-
16 levels are not enough for naive uniform quantization. The limited representational capacity requires sophisticated techniques to maintain model quality. A single outlier weight can corrupt the entire quantization scale, making naive INT4 unusable in practice.
-
Group-wise quantization is needed for INT4 success. By using separate scale factors for groups of 32-128 weights, outliers affect only their local group rather than the entire tensor. This spatial isolation of outlier damage is the foundational innovation that makes 4-bit quantization practical.
-
NF4 format outperforms uniform INT4 for normally distributed weights by placing quantization levels to match the weight distribution. By so each of the 16 levels is equally likely to be used, NF4 maximizes the information extracted from the 4-bit budget. This format, introduced with QLoRA, has become the de facto standard for 4-bit inference.
-
Double quantization reduces the memory overhead from scale factors by quantizing the scales themselves. The two-level hierarchy (INT4 weights, INT8 scales, FP32 meta-scales) approaches true 4 bits per weight while maintaining the accuracy benefits of group-wise quantization.
-
Model size and task complexity determine quantization tolerance. Larger models (30B+) typically maintain quality at INT4, while smaller models may need INT8 or mixed precision strategies. Tasks requiring precise numerical reasoning are more sensitive to quantization errors than tasks involving pattern recognition.
The next chapter covers GPTQ, a calibration-based quantization method that uses second-order information to find optimal weight quantization, often achieving better accuracy than the simpler methods discussed here. If NF4 is like using a well-designed ruler, GPTQ is like custom-designing a ruler for each specific layer based on data about how that layer is used.
Quiz
Ready to test your understanding? Take this quick quiz to reinforce what you've learned about INT4 quantization techniques.
INT4 Quantization
Reference
Citation details
Cite or share this article.
Continue with the full handbook
This chapter is part of Language AI Handbook. Use the handbook page to browse the complete table of contents and continue reading in sequence.
Explore Language AI HandbookStay up to date
Get articles, book updates, and news delivered to your inbox.
No spam, unsubscribe anytime.
Join the community
Sign in to remove popups, track your reading progress, and join the discussion.
Comments
No comments yet. Be the first to share your thoughts!