Vector Similarity Search: Metrics & Approximate Methods

In the previous chapter, we explored how embedding models transform text into dense vectors that capture semantic meaning. In the chapter on dense retrieval, we saw how these embeddings power modern search by finding documents whose vectors are "close" to a query vector. However, we need to define what "close" means and how to find the closest vectors efficiently in large collections.

This is the problem of vector similarity search. At small scales, it is trivially solved: compare the query to every vector in your collection and return the best matches. For large-scale RAG systems, this brute-force approach is often too slow. A collection of 10 million documents with 768-dimensional embeddings requires roughly 7.7 billion floating-point operations per query, just for a single distance metric. Handling thousands of concurrent users requires a more efficient approach.

This chapter lays the groundwork for efficient vector search. We start by examining the distance metrics that define what similarity means in vector space, going deep into the geometry and practical implications of each. Then we contrast exact search (which guarantees finding the true nearest neighbors) with approximate search (which trades a small amount of accuracy for dramatic speed improvements). We survey the families of algorithms that make approximate search possible and walk through practical code for each. Finally, we examine the libraries that implement these ideas and the practical limitations you will encounter in production systems. The specific index structures that make approximate search possible, including HNSW and IVF, receive dedicated chapters that follow.

Before you can search for the "most similar" vectors, you need to define a measure of similarity. This decision shapes the entire retrieval pipeline. The metric you choose determines which documents appear at the top of your search results, how your index structures organize the vector space, and ultimately how effective your retrieval pipeline will be. Different metrics capture different geometric relationships between vectors, and understanding these relationships in detail is needed for building high-quality search systems.

At a high level, the question of similarity can be split into two perspectives. One perspective asks: "Are these two vectors pointing in roughly the same direction?" This is a question about orientation, about the angle between the arrows in vector space. The other perspective asks: "How far apart are these two vectors as points in space?" This is a question about position, about the absolute gap between them. These perspectives can yield different answers for the same pair of vectors. Knowing which question matters for your application helps in choosing the right metric.

Before examining each metric in detail, it helps to build intuition for the geometry of high-dimensional spaces. In two or three dimensions, vectors are easy to visualize as arrows. In 768 dimensions, you cannot draw the picture, but the same geometric relationships hold. A vector is still a direction and a magnitude. Two vectors still form an angle. The distance between their tips is still well-defined. Every piece of geometry we develop here applies exactly in high dimensions, even when our visual intuition fails.

Cosine similarity measures the angle between two vectors, ignoring their magnitudes entirely. The core intuition is geometric: imagine two arrows emanating from the origin in a high-dimensional space. If the arrows point in the same direction, regardless of whether one is short and the other is long, we consider them maximally similar. If they point in perpendicular directions, they share no similarity at all. And if they point in opposite directions, they are maximally dissimilar. This is precisely what the cosine of the angle between two vectors captures.

For vectors $\mathbf{a}$ and $\mathbf{b}$ in $\mathbb{R}^d$, cosine similarity is defined as:

where:

• $\mathbf{a}, \mathbf{b}$: the input vectors being compared
• $d$: the dimensionality of the vector space
• $a_i, b_i$: the scalar components of vectors $\mathbf{a}$ and $\mathbf{b}$ at dimension $i$
• $\mathbf{a} \cdot \mathbf{b}$: the dot product, representing unnormalized alignment
• $\|\mathbf{a}\|$: the Euclidean length ($L_2$ norm) of vector $\mathbf{a}$
• $\sum_{i=1}^{d}$: the summation across all dimensions

To understand what this formula is really doing, let's break it apart. The numerator, the dot product $\mathbf{a} \cdot \mathbf{b}$, computes a raw measure of how well the two vectors align. It multiplies corresponding components and sums the results. When both vectors have large positive values in the same dimensions, the dot product grows large and positive. When one vector is positive where the other is negative, those dimensions contribute negative terms, pulling the sum down. The dot product, in isolation, reflects both alignment and magnitude: longer vectors produce larger dot products even at the same angle.

The denominator corrects for this magnitude dependence. By dividing by the product of the two vector norms, we effectively scale the dot product so that it reflects only the angular relationship. Geometrically, this is equivalent to first projecting both vectors onto the unit sphere (normalizing them to length 1) and then computing their dot product. The result is the cosine of the angle $\theta$ between them.

The result ranges from $-1$ (pointing in opposite directions) through $0$ (orthogonal) to $+1$ (pointing in the same direction). In practice, most embedding models produce vectors that occupy a relatively narrow region of the space, so similarity values for relevant documents often fall between 0.5 and 0.95. Two completely unrelated documents might still achieve cosine similarities around 0.2-0.4 simply because language embeddings cluster in a particular region of the high-dimensional sphere, a phenomenon called anisotropy that we discussed in the chapter on BERT representations.

Why is cosine similarity the default for text embeddings? Because it focuses on the direction of the vector rather than its length. Two documents about the same topic should be considered similar even if one has a larger-magnitude embedding. By normalizing out magnitude, cosine similarity captures pure semantic orientation. Consider two sentences like "The cat sat on the mat" and "A feline rested upon the rug." An embedding model should map these to vectors pointing in nearly the same direction. This reflects their shared meaning. Even if the model produces vectors of slightly different lengths for these two inputs, cosine similarity will correctly identify them as highly similar because their angular separation is small.

The metric is also well-suited to the query-document asymmetry that characterizes retrieval. Query vectors often represent short, terse expressions of information need, while document vectors represent long, rich passages of text. The absolute magnitude of these vectors might differ substantially, but if they cover the same topic, their directions should align. Normalizing out magnitude makes this comparison fair.

The dot product is the simplest and most computationally inexpensive of all vector similarity measures. It requires no normalization step: you simply multiply corresponding components and sum:

where:

• $\mathbf{a}, \mathbf{b}$: the input vectors
• $d$: the dimensionality of the vector space
• $a_i, b_i$: the scalar components of vectors $\mathbf{a}$ and $\mathbf{b}$ at dimension $i$
• $\sum_{i=1}^{d}$: the summation across all $d$ dimensions
• $\mathbf{a} \cdot \mathbf{b}$: the aggregate alignment score, which increases with both directional similarity and vector length

Unlike cosine similarity, the dot product does account for vector magnitude. This means a longer vector can score higher even if its direction is slightly less aligned. To see why, think of it geometrically: the dot product of two vectors equals $\|\mathbf{a}\| \, \|\mathbf{b}\| \, \cos\theta$. When the norms are not divided out, a vector that is twice as long contributes twice as much to the final score, all else being equal. This makes the dot product sensitive to both how well two vectors agree in direction and how "strong" or "confident" each vector's representation is.

When would you want this behavior? When magnitude carries information. Some embedding models and retrieval systems train embeddings so that the vector norm encodes confidence or relevance strength. For example, a model might learn to produce longer vectors for documents that are more central to a topic and shorter vectors for documents that touch on the topic only tangentially. In these cases, dot product is the correct metric because it rewards both directional alignment and strong confidence signals. A highly relevant document with a long vector and good directional alignment will outscore a marginally relevant document, even if the marginal document happens to have a slightly better angle.

There is an important relationship between these two metrics in practice. If your vectors are $L_2$-normalized (i.e., $\|\mathbf{a}\| = \|\mathbf{b}\| = 1$), then the dot product and cosine similarity are identical:

where:

• $\mathbf{a}, \mathbf{b}$: the normalized input vectors
• $\|\mathbf{a}\|, \|\mathbf{b}\|$: the lengths of the vectors (both equal to 1)
• $\theta$: the angle between vectors $\mathbf{a}$ and $\mathbf{b}$

The derivation proceeds by recalling that the geometric definition of the dot product relates it to the product of the vector magnitudes and the cosine of the angle between them. When both vectors lie on the unit sphere, their magnitudes are exactly 1, and the product collapses to the cosine of the angle alone.

This is why many systems pre-normalize their embeddings. It lets you use the cheaper dot product operation while getting cosine similarity results, and it opens the door to optimized index structures that assume unit-norm vectors. The dot product avoids the division and square root operations required by cosine similarity, which makes it faster in tight inner loops where billions of comparisons are performed. By paying the one-time cost of normalization at indexing time, you gain this computational advantage at every subsequent query.

The computational savings of the dot product over cosine similarity might seem trivial, but at scale they matter. For 10 million vectors at dimension 768, each dot product requires 768 multiply-add operations. Cosine similarity requires those same operations plus two norm computations (each requiring 768 squarings, a sum, and a square root). When you are running this computation billions of times, the accumulated savings are significant.

Euclidean distance ($L_2$ distance) takes an entirely different perspective from the angle-based metrics we have discussed so far. Instead of asking how well two vectors align directionally, it asks: how far apart are these two points in space? It measures the straight-line distance between two points, the length of the shortest path connecting them:

where:

• $\mathbf{a}, \mathbf{b}$: the input vectors
• $d$: the dimensionality of the vector space
• $a_i, b_i$: the scalar components of vectors $\mathbf{a}$ and $\mathbf{b}$ at dimension $i$
• $a_i - b_i$: the difference between the scalar components along dimension $i$
• $(a_i - b_i)^2$: the squared difference, which makes negative differences positive and penalizes large outliers
• $\sum_{i=1}^{d}$: the sum of squared differences across all dimensions
• $\sqrt{\dots}$: the square root, which converts the sum of squares back to the original units (linear distance)

This is the most intuitive metric: it corresponds to the physical distance you would measure with a ruler. It generalizes the familiar Pythagorean theorem from two or three dimensions to arbitrarily high-dimensional spaces. In two dimensions, the distance between points $(x_1, y_1)$ and $(x_2, y_2)$ is $\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$. The formula above extends this same idea to $d$ dimensions, summing the squared differences along every axis and taking the square root of the total.

Euclidean distance is sensitive to both direction and magnitude. Two vectors can have high cosine similarity (similar direction) but large Euclidean distance (very different magnitudes). Consider a query vector $\mathbf{q}$ and a document vector $\mathbf{v} = 10\mathbf{q}$. Their cosine similarity is a perfect 1.0, since they point in exactly the same direction. But their Euclidean distance is $9\|\mathbf{q}\|$, which could be quite large. This illustrates the basic distinction: cosine similarity sees these as identical, while Euclidean distance sees them as far apart. Which perspective is "correct" depends entirely on whether magnitude carries meaningful information in your embedding space.

Another important property of Euclidean distance is its sensitivity to outlier dimensions. Because differences are squared before summing, a single dimension with a large discrepancy can dominate the total distance. For example, if two 768-dimensional vectors agree perfectly in 767 dimensions but differ by 10 in the remaining dimension, the squared Euclidean distance is $10^2 = 100$, equivalent to disagreeing by 0.36 across all 768 dimensions. This squaring effect means Euclidean distance penalizes concentrated disagreement more heavily than diffuse disagreement. Whether this is desirable depends on the structure of your embedding space.

For normalized vectors, Euclidean distance and cosine similarity are monotonically related. This connection is one of the most important results in vector similarity search, because it means that, under normalization, the choice between these two metrics does not change the ranking of results. The derivation proceeds by expanding the squared Euclidean distance:

where:

• $\|\mathbf{a} - \mathbf{b}\|^2$: the squared Euclidean distance
• $\mathbf{a}, \mathbf{b}$: the normalized input vectors (length of 1)
• $\theta$: the angle between vectors $\mathbf{a}$ and $\mathbf{b}$

The key step is the expansion in the second line. When you compute $(\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} - \mathbf{b})$, you are effectively computing $\mathbf{a} \cdot \mathbf{a} - 2\mathbf{a} \cdot \mathbf{b} + \mathbf{b} \cdot \mathbf{b}$, which is $\|\mathbf{a}\|^2 - 2\mathbf{a} \cdot \mathbf{b} + \|\mathbf{b}\|^2$. For unit vectors, the squared norms are both 1, and the dot product is $\cos\theta$, giving us the clean relationship $2 - 2\cos\theta$.

So $d_{\text{L2}} = \sqrt{2 - 2\cos\theta}$. Higher cosine similarity means smaller Euclidean distance. This means that for normalized vectors, searching by minimum Euclidean distance produces the same ranking as searching by maximum cosine similarity. The two metrics induce identical orderings over all candidate vectors, differing only in the numerical values they assign. In practice, many libraries use squared Euclidean distance ($d_{\text{L2}}^2$) to avoid the square root computation, since it preserves the same ordering. The square root is a monotonically increasing function, so removing it does not affect which vector is closest or the relative ranking of candidates.

Manhattan distance ($L_1$ distance) takes yet another approach to measuring separation between points, one that treats each dimension independently and sums their contributions linearly rather than quadratically:

where:

• $\mathbf{a}, \mathbf{b}$: the input vectors
• $d$: the dimensionality of the vector space
• $a_i, b_i$: the scalar components of vectors $\mathbf{a}$ and $\mathbf{b}$ at dimension $i$
• $|a_i - b_i|$: the absolute difference along dimension $i$
• $\sum_{i=1}^{d}$: the sum of these linear differences, representing the total "grid-based" distance

Named after the grid-like street layout of Manhattan, where travel between two points must follow the rectangular street grid rather than cutting diagonally, this metric captures a different notion of separation. Imagine traveling from one intersection to another: you can only move north-south or east-west, never diagonally. The total distance you travel is the sum of horizontal and vertical displacements, which is exactly what the $L_1$ norm computes.

This metric is less common for dense text embeddings but appears in some specialized contexts. It is less sensitive to outliers in individual dimensions than Euclidean distance, since it does not square the differences. Recall that in Euclidean distance, a single dimension with a discrepancy of 10 contributes 100 to the sum, whereas in Manhattan distance, it contributes only 10. This means Manhattan distance treats every unit of disagreement equally, regardless of whether it is concentrated in one dimension or spread across many. For representations where individual dimensions can occasionally take on extreme values, such as certain sparse or quantized embeddings, this reduced sensitivity can be advantageous.

Manhattan distance also has a useful computational property: on hardware with SIMD (Single Instruction Multiple Data) vector extensions, computing absolute values and summing them is often slightly faster than computing squared differences, because the squaring step is replaced by an absolute value operation. For very tight performance budgets, this can matter.

A final metric worth mentioning, though it occupies a specialized niche, is Hamming distance. Used with binary vector representations, it counts the number of bit positions where two vectors differ:

where:

• $\mathbf{a}, \mathbf{b}$: binary vectors with elements in $\{0, 1\}$
• $\mathbb{1}[\cdot]$: the indicator function, equal to 1 when the condition is true and 0 otherwise
• $\sum_{i=1}^{d}$: the count of positions where the two vectors disagree

Hamming distance is important because modern CPUs can compute it extremely efficiently using the POPCNT instruction (population count, which counts set bits). By representing vectors as bit arrays and computing Hamming distance via XOR followed by POPCNT, you can compare thousands of binary vectors in the time it takes to compare a handful of float32 vectors. This enables retrieval systems that sacrifice some precision for dramatic throughput gains. Techniques like binary neural hashing learn to project continuous embeddings into binary codes that preserve approximate similarity under Hamming distance.

The "correct" metric depends on how your embeddings were trained. This is a point worth emphasizing: the metric is not a free parameter you can tune independently. During training, the embedding model learns to arrange vectors in space so that a specific notion of similarity (defined by the training loss) corresponds to semantic relatedness. If the model was trained to make relevant document-query pairs have high cosine similarity, then the learned geometry of the embedding space is shaped around angular relationships. Using a different metric at search time than the one used during training will degrade retrieval quality, because you would be measuring a geometric property that the model did not optimize for.

Most modern sentence embedding models, including those we discussed in the previous chapter on embedding models, are trained with cosine similarity as the objective and expect you to use cosine similarity (or equivalently, dot product on normalized vectors) at search time. Always check the documentation for your specific model.

The key guidelines are:

• Cosine similarity / normalized dot product: Default choice for most sentence embedding models (Sentence-BERT, E5, GTE, etc.)
• Dot product: Use when your model explicitly trains with dot product and encodes meaningful information in vector magnitude
• Euclidean distance: Common in computer vision embeddings and some specialized models; equivalent to cosine for normalized vectors
• Manhattan distance: Rarely the best choice for text embeddings, but useful for certain sparse or quantized representations
• Hamming distance: For binary embeddings where extreme throughput is required and some accuracy loss is acceptable

The simplest approach to finding the $k$ nearest neighbors of a query vector is exhaustive search: compute the distance between the query and every vector in the collection, then return the $k$ closest ones. Despite its simplicity, this approach serves a useful role in the vector search ecosystem. It provides a correctness baseline against which all approximate methods are measured, and it remains the practical choice for collections small enough that its linear cost is acceptable.

Given a query vector $\mathbf{q} \in \mathbb{R}^d$ and a collection of $n$ vectors $\{\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n\}$, each also in $\mathbb{R}^d$, exact search performs the following:

1. Compute $\text{distance}(\mathbf{q}, \mathbf{v}_i)$ for all $i = 1, \ldots, n$
2. Sort or partially sort the results to find the $k$ smallest distances
3. Return the corresponding $k$ vectors (and their identifiers)

The first step is where nearly all the computation happens. For each of the $n$ vectors in the collection, we must compute a distance or similarity score against the query. Each such computation involves $d$ multiplications and $d-1$ additions (for the dot product), plus any additional operations required by the specific metric (normalization for cosine similarity, subtraction and squaring for Euclidean distance). The computational cost is therefore $O(n \cdot d)$ for the distance computations, plus $O(n \log k)$ for maintaining a heap of the top $k$ results. For typical embedding dimensions ($d = 384$ to $1536$) and collection sizes ($n$ in the millions), the $O(n \cdot d)$ term dominates.

The second step, finding the top $k$ results, is handled efficiently by maintaining a max-heap (for distances, where we want the smallest) or min-heap (for similarities, where we want the largest) of size $k$. As each new distance is computed, it is compared against the worst element in the heap. If the new distance is better, it replaces the worst element. This avoids the $O(n \log n)$ cost of fully sorting all distances and instead requires only $O(n \log k)$ operations, which is significantly cheaper when $k$ is small relative to $n$.

Modern CPUs expose SIMD (Single Instruction Multiple Data) instruction sets like AVX2 and AVX-512 that process multiple floating-point values simultaneously. An AVX2 register holds 8 float32 values, so a single instruction can multiply or add 8 pairs of components at once. This means that the effective number of clock cycles per dot product is $d/8$ rather than $d$, an 8x theoretical speedup. In practice, combined with careful memory layout (storing vectors in row-major order for sequential access) and vectorized operations, libraries like FAISS achieve near-peak floating-point throughput on dot product computations.

The memory bandwidth story is equally important. For an exact search over 10 million 384-dimensional vectors, the total data that must be read from RAM is $10^7 \times 384 \times 4 \approx 15$ GB. Modern CPUs have memory bandwidth around 50-100 GB/s, so even if the computation were free, reading that much data takes 0.15-0.3 seconds per query. This memory bandwidth ceiling is often the dominant bottleneck for exact search on large collections, not the arithmetic.

GPUs change this calculus significantly. A modern GPU (like an NVIDIA A100) has 2 TB/s of memory bandwidth and 312 TFLOPS of tensor core throughput. Reformulating the distance computations as a matrix-matrix multiplication allows batching multiple queries together and saturating the GPU's capabilities. For batches of 100 queries over 10 million vectors at dimension 768, a GPU can sustain query rates that CPU-based exact search cannot match. FAISS's GPU backend exploits this by converting the batch search into a matrix multiplication $\mathbf{Q} \times \mathbf{D}^T$ where $\mathbf{Q}$ is the query matrix and $\mathbf{D}$ is the document matrix.

Exact search guarantees returning the true nearest neighbors. There are no missed relevant documents, no tuning parameters for recall, and no possibility that the correct answer was overlooked. Every vector in the collection is examined, so the algorithm has complete knowledge of the entire search space. This makes it the gold standard for evaluating approximate methods: when we report recall@k for an ANN algorithm, we are measuring how often it agrees with the results that exact search would have returned.

However, it scales linearly with collection size, which makes it inefficient for large datasets. Let's think through the numbers to develop a concrete sense of where the boundary lies. If you have 1 million vectors of dimension 768, a single query requires roughly 768 million multiply-add operations. On modern hardware with SIMD instructions, you can sustain around 10-50 billion floating-point operations per second on a single CPU core. That puts brute-force at roughly 15-75 milliseconds per query, which is potentially acceptable for some applications. But scale to 100 million vectors and you are looking at 1.5-7.5 seconds per query, which is far too slow for interactive use. The linear scaling with collection size means that every 10x increase in collection size produces a 10x increase in query time, with no way to mitigate this short of faster hardware.

The practical crossover point where you should switch from exact to approximate search depends on your latency budget and query volume. For a RAG system serving interactive users with a 100ms latency budget and a collection of a few hundred thousand documents, exact search on a single CPU may be fast enough. For a production system serving millions of queries per day over tens of millions of documents, approximate methods are needed.

Exact search requires storing all $n$ vectors in memory, since any vector could potentially be a nearest neighbor and must be accessible for the distance computation. For $n$ vectors of dimension $d$ stored as 32-bit floats, the memory requirement is:

where:

• $n$: the number of vectors in the collection
• $d$: the dimensionality of each vector
• $4$: the size in bytes of a standard 32-bit floating-point number

This formula reflects the fact that each vector is simply a flat array of $d$ floating-point values, and the full collection is $n$ such arrays stored contiguously. There is no overhead for index structures in exact search: the "index" is just the raw matrix of vectors.

For 10 million vectors at dimension 768, that is about 28.8 GB. This is feasible on a single large-memory machine but becomes challenging at larger scales. We will see in the chapter on Product Quantization how vector compression can dramatically reduce this memory footprint.

The main point behind approximate nearest neighbor (ANN) search is that you rarely need the exact nearest neighbors. In most retrieval applications, the downstream task (such as generating an answer from retrieved documents) is reliable to small perturbations in the retrieved set. If the true 3rd-closest document has a similarity of 0.873 and the ANN algorithm returns a document with similarity 0.871 instead, the difference is negligible for downstream generation. The answer produced by the language model will be virtually indistinguishable regardless of which document was included.

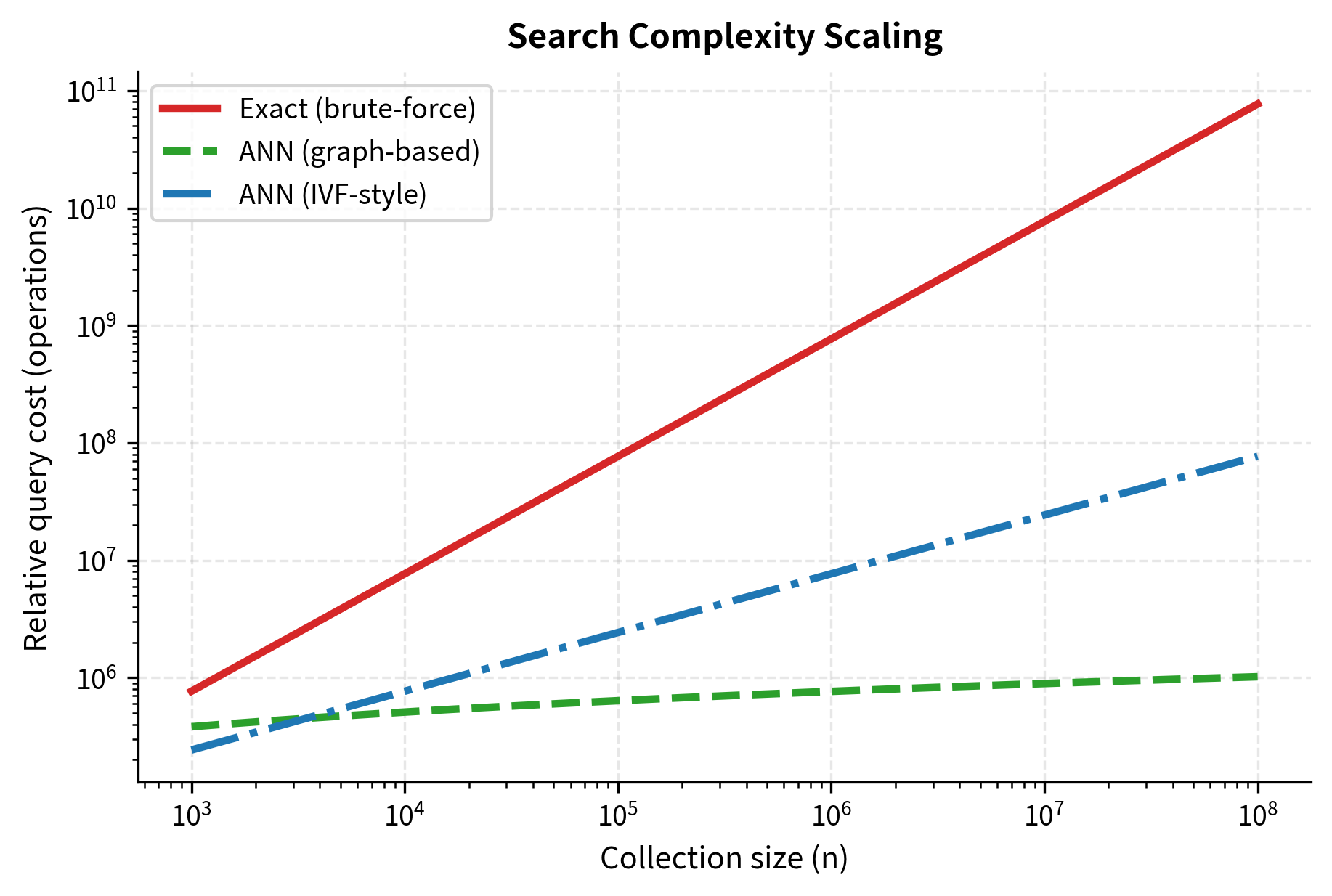
By accepting this small accuracy trade-off, ANN algorithms can reduce search time from linear in $n$ to sublinear, often logarithmic or even near-constant. This is a dramatic improvement. Whereas exact search over 100 million vectors might take several seconds, a well-tuned ANN index can return results in a few milliseconds, a speedup of three orders of magnitude. This is what makes real-time retrieval over massive collections feasible.

Every ANN algorithm offers knobs that control this trade-off. Turning the knob toward more accuracy means searching more of the index, examining more candidates, and spending more time verifying potential neighbors. Turning it toward more speed means searching less of the index, examining fewer candidates, and accepting a higher risk of missing relevant results. The art of ANN tuning is finding the sweet spot where recall is high enough (typically 95-99%) while latency meets your application requirements.

This trade-off is not binary: it is a continuous spectrum. For a given index structure, you can choose any operating point along a curve that runs from very fast and low recall to slow and perfect recall. This trade-off is usually visualized as a recall-vs-queries-per-second curve. A well-designed index will have an "elbow" where you get most of the recall for a modest time investment, with diminishing returns beyond that point. The ideal operating point is typically just past this elbow, where you have captured the large majority of relevant neighbors while keeping latency well within your budget.

Understanding this trade-off geometrically helps build intuition. The reason approximate methods can be fast is that they avoid examining regions of the space that are unlikely to contain relevant neighbors. An IVF index, for instance, identifies the cluster whose centroid is closest to the query and then searches only within that cluster. This works because nearby vectors tend to cluster together in the learned embedding space. The approximation error arises when a true nearest neighbor happens to fall in a different cluster, which occurs occasionally near cluster boundaries.

ANN algorithms generally fall into several broad categories, each based on a different strategy for avoiding the exhaustive scan over all vectors. Understanding these families at a conceptual level helps you choose an approach that meets your accuracy target at the required scale on the available hardware.

Tree-Based MethodsLink Copied

Tree-based methods partition the vector space recursively using a tree structure, then search by traversing only the branches of the tree near the query. The canonical example is the KD-tree (k-dimensional tree), which works by choosing one dimension at each level of the tree and splitting vectors by their median value along that dimension. To search, you traverse from the root toward the leaf containing the query, then backtrack to check neighboring branches when necessary.

KD-trees work well in low dimensions (up to around 10-20) but suffer severely from the curse of dimensionality in high-dimensional spaces. In high dimensions, almost every data point is "near" the query in the sense that backtracking is required at nearly every node, causing the search to degenerate toward brute force. The fraction of the space you can prune away shrinks exponentially with dimension.

Random projection trees (and their more sophisticated variant, the randomized KD-tree used in FLANN) address this by choosing split dimensions randomly rather than greedily, which provides better coverage of the vector space. Spotify's Annoy library uses a forest of random projection trees and averages the results across multiple trees to achieve good recall. The key insight is that by building many trees with different random splits, you reduce the probability that a true neighbor falls in an inaccessible region of any single tree.

Locality-Sensitive HashingLink Copied

Locality-Sensitive Hashing (LSH) takes a different approach, mapping nearby vectors to the same hash bucket with high probability and distant vectors to different buckets with high probability. The definition of "nearby" is formalized by the sensitivity of the hash function to the chosen metric.

For cosine similarity, a classic LSH scheme uses random hyperplanes. Each hyperplane divides the space into two half-spaces. A vector is assigned a bit based on which side of the hyperplane it falls on. With $b$ hyperplanes, each vector receives a $b$-bit hash code. Two vectors with high cosine similarity tend to fall on the same side of each hyperplane, creating similar hash codes, while dissimilar vectors tend to disagree on more bits. At query time, you compute the query's hash code and retrieve all vectors from the matching bucket, then compute exact distances among this candidate set.

The challenge with LSH is that a single hash table has limited recall, because some true neighbors inevitably fall in different buckets (false negatives). The standard solution is to use multiple hash tables with different random hyperplanes and take the union of all retrieved candidates. With $L$ tables, a true near neighbor must end up in the wrong bucket in all $L$ tables to be missed, which becomes exponentially unlikely as $L$ increases. However, increasing $L$ also increases both memory usage and query time, creating the familiar speed-recall trade-off. LSH systems typically require $L = 10$-$50$ tables for competitive recall, which makes them memory-intensive relative to graph-based methods.

Graph-Based MethodsLink Copied

Graph-based methods build a proximity graph where each vector is a node and edges connect each vector to its approximate nearest neighbors. To answer a query, you start at some entry point (often a randomly chosen or centrally located vector) and greedily move toward the query by repeatedly choosing the neighbor that is closest to it. This greedy traversal follows a path through the graph from the starting node toward the region of space containing the nearest neighbors.

The key challenge in graph-based search is escaping local minima: the greedy path might get stuck at a node that is locally close to the query but not globally among the nearest neighbors. The solution is to maintain a candidate list during traversal, exploring multiple frontier nodes simultaneously rather than committing to a single greedy path. This beam-search-like approach explores a broader region at the cost of examining more nodes.

HNSW (Hierarchical Navigable Small World) graphs, which we cover in the next chapter, solve the local minimum problem elegantly by building a multi-layer graph structure inspired by skip lists. The top layers of the graph contain long-range connections that enable fast coarse navigation, while the bottom layer contains short-range connections for fine-grained refinement. This hierarchy makes graph-based search efficient even in high dimensions and is currently the dominant ANN algorithm in production systems.

Quantization-Based MethodsLink Copied

Quantization-based methods compress vectors into compact binary or integer codes, then perform search in the compressed space. The extreme version is binary quantization, which replaces each float32 component with a single bit (1 for positive, 0 for negative). This reduces memory by 32x and enables extremely fast Hamming distance computation but sacrifices significant accuracy.

Product Quantization (PQ) is a more principled approach that divides the vector into $m$ equal sub-vectors, learns a small codebook for each sub-vector separately, and represents each sub-vector by the index of its nearest codeword. With $m = 8$ sub-vectors and $256$ codewords each, each vector is compressed from 768 float32 values (3 KB) to 8 bytes, a compression ratio of 384x. Distances can then be computed using precomputed lookup tables rather than full vector arithmetic, dramatically accelerating the comparison step. The PQ approximation introduces error, but for large collections where memory is the bottleneck, this trade-off is often worthwhile.

Inverted File MethodsLink Copied

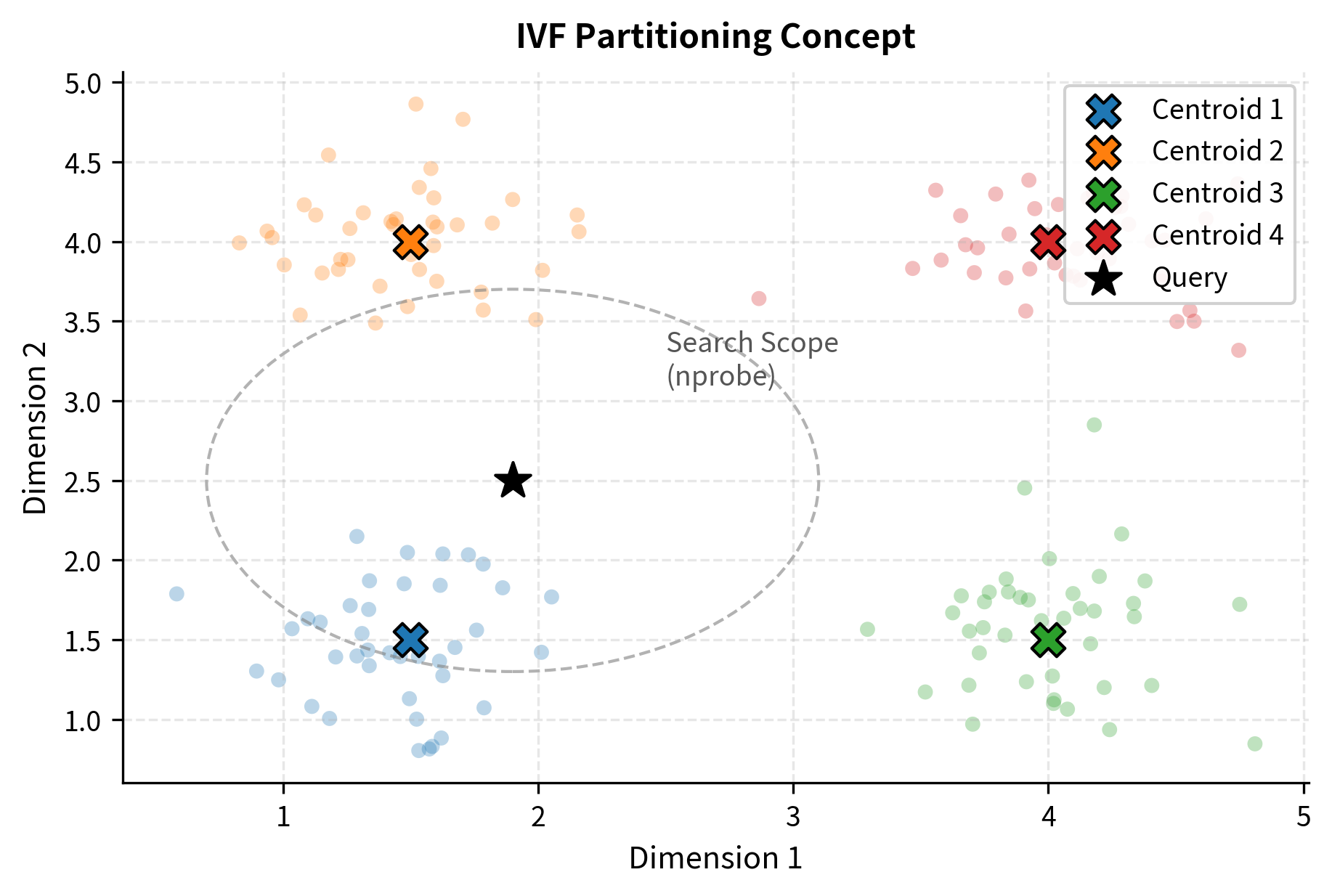
Inverted file methods partition vectors into clusters using k-means or similar algorithms, then at query time, search only the clusters closest to the query. This is the IVF (Inverted File) approach, directly analogous to the inverted index in keyword search but operating on vector clusters instead of term occurrence lists.

The partitioning step maps each vector to its nearest cluster centroid. At search time, the query is compared against all $K$ centroids to find the $n_{\text{probe}}$ nearest clusters, and then only vectors within those clusters are examined. If $n_{\text{probe}} = 1$ and each cluster contains $n/K$ vectors, the search examines $n/K$ vectors instead of $n$, a $K$-fold speedup. With $n_{\text{probe}} = \sqrt{K}$ (a common heuristic), the search examines $\sqrt{n}$ vectors, achieving $O(\sqrt{n})$ effective cost.

In practice, production systems often combine multiple approaches. FAISS's IVF_PQ index uses inverted file partitioning for coarse navigation, then applies product quantization to compress the vectors within each partition for efficient in-cluster comparison. Understanding the individual building blocks is needed for understanding these combinations.

To compare ANN algorithms and tune their parameters, we need a principled way to measure how close an approximate result is to the true answer. The standard metric for ANN quality is recall@k, which directly measures the overlap between the approximate results and the exact results:

where:

• $\text{ANN results}$: the set of $k$ document identifiers returned by the approximate search
• $\text{true } k\text{-NN}$: the set of $k$ document identifiers returned by an exact (brute-force) search
• $|\dots|$: the cardinality (count) of the intersection between the two sets
• $k$: the number of neighbors requested

The numerator counts how many of the true nearest neighbors appear in the ANN result set. The denominator normalizes by $k$, the total number of neighbors requested, so that the metric always falls between 0 and 1. A recall of 1.0 means the ANN algorithm returned exactly the same set of neighbors as exact search (though possibly in a different order). A recall of 0.0 means it missed every single true neighbor.

To make this concrete with an example: if the true 10 nearest neighbors are documents {A, B, C, D, E, F, G, H, I, J} and your ANN algorithm returns {A, B, C, D, E, F, G, H, K, L}, then $\text{recall@}10 = 8/10 = 0.80$. The algorithm found 8 of the 10 true nearest neighbors, missing I and J while incorrectly including K and L. Note that the documents K and L are not necessarily irrelevant; they are simply not among the true top 10. In most practical scenarios, the documents that ANN returns instead of the missed true neighbors tend to have very similar scores, since the "mistakes" typically involve swapping neighbors that are nearly equidistant from the query.

For RAG applications, $\text{recall@}10$ values above 0.95 are typically sufficient. The reranking stage that follows retrieval (which we will cover later in this part) can further compensate for occasional misses. When evaluating your own system, it is useful to measure recall at multiple values of $k$, because the behavior can differ. An index might have recall@1 of 0.85 (sometimes missing the single best match) but recall@10 of 0.98 (almost always including the true top results when you fetch 10). For RAG, where you typically retrieve 5-20 documents and pass them all to the language model, the recall@k for your actual retrieval size is the most relevant metric.

One subtlety that benchmarks often obscure is that ANN performance depends heavily on the structure of your data. ANN algorithms exploit the fact that real embeddings have natural clustering structure: documents about similar topics cluster together, and queries tend to fall near relevant documents in this clustered space. When this structure is strong, as it is for diverse corpora with well-separated topics, IVF and graph-based methods achieve excellent recall because cluster boundaries rarely separate truly similar documents.

However, when the data is more uniformly distributed (less natural clustering), or when queries fall near cluster boundaries, recall degrades. This is why it is important to benchmark ANN methods on your actual data and query distribution, not just on standard benchmarks. The ANN-Benchmarks suite (ann-benchmarks.com) provides standardized comparisons, but your production recall may differ from these numbers depending on the nature of your documents and queries.

Let's make these metrics concrete with a small example that illustrates the key differences between direction-based and position-based measures. Suppose we have a query vector and four document vectors, all in $\mathbb{R}^3$ for visualization simplicity. The low dimensionality lets us reason about the geometry directly, and the principles we observe generalize straightforwardly to the hundreds of dimensions used in real embeddings.

These four vectors were chosen deliberately to illustrate specific geometric relationships. Notice that $\mathbf{v}_2 = 3 \times \mathbf{q}$, so it points in exactly the same direction but has 3 times the magnitude. This makes it a perfect test case for the distinction between direction-based and position-based metrics: any direction-based metric will consider $\mathbf{v}_2$ identical to $\mathbf{q}$, while any position-based metric will see them as far apart. Meanwhile, $\mathbf{v}_4 = -\mathbf{q}$, pointing in the exact opposite direction, which should produce the worst possible cosine similarity. The vector $\mathbf{v}_1$ is the subtlest case: it is close to $\mathbf{q}$ in both direction and magnitude, differing only by small perturbations in each component. Finally, $\mathbf{v}_3$ points in a substantially different direction, with a large component in the third dimension where $\mathbf{q}$ has only a small value.

Before computing anything, we can reason geometrically about what to expect. Cosine similarity between $\mathbf{q}$ and $\mathbf{v}_2$ should be 1.0 (identical direction), while cosine similarity between $\mathbf{q}$ and $\mathbf{v}_4$ should be $-1.0$ (opposite direction). Meanwhile, $\mathbf{v}_1$ is close to $\mathbf{q}$ in both direction and magnitude, so it should also have high cosine similarity, though not a perfect 1.0.

Euclidean distance between $\mathbf{q}$ and $\mathbf{v}_1$ should be small (they are nearby), while the distance between $\mathbf{q}$ and $\mathbf{v}_2$ will be large despite their identical directions (because $\mathbf{v}_2$ is far away in absolute terms). This is the signature behavior that distinguishes position-based from direction-based metrics.

After normalization, cosine similarity and dot product produce identical values, confirming the mathematical relationship we derived earlier: for unit vectors, $\mathbf{a} \cdot \mathbf{b} = \cos\theta$. And the rankings from all three metrics now agree: the vectors with higher cosine similarity also have smaller Euclidean distance, exactly as the identity $d_{\text{L2}}^2 = 2 - 2\cos\theta$ predicts. Notice in particular that $\mathbf{v}_2$, which was far from the query before normalization, now sits at exactly the same point as the normalized query, with Euclidean distance 0.0. Normalization collapsed the magnitude information and left only direction.

This is the practical reason why normalizing embeddings before indexing is so common: it makes the choice of metric irrelevant. Once all vectors lie on the unit sphere, cosine similarity, dot product, and Euclidean distance all induce the same ranking over candidates. You can then choose whichever metric your library computes most efficiently, typically the dot product, without worrying about whether it matches the conceptual notion of similarity your model was trained with.

Another way to understand how metrics differ is to examine their distribution over a realistic embedding collection. When you compute all pairwise similarities in a real embedding collection, the distribution reveals the geometry of the embedding space: how tight the clusters are, how much separation exists between topics, and what similarity values to expect for relevant versus irrelevant documents.

The distribution shows how vector search works at scale. Most documents in the collection are only weakly similar to any given query: the bulk of cosine similarities cluster near zero. The relevant documents (simulated here as vectors near the query direction) form a distinct right tail. A retrieval system needs to identify this tail efficiently, which is why even small differences in the similarity metric can affect which documents make it into the retrieved set.

Understanding the computational complexity of different search strategies helps you make informed decisions about which approach fits your scale. The differences between exact and approximate search are not marginal: they are qualitative changes in how query cost grows with collection size. Exact search grows linearly, meaning that doubling the collection size doubles the query time. Approximate methods grow sublinearly, meaning that doubling the collection size increases query time by much less than a factor of two. At large scales, this distinction is the difference between a system that responds in milliseconds and one that takes seconds.

The table below summarizes the trade-offs across the major search strategies. Each row captures a different aspect of system behavior, from query-time latency to memory consumption, and the columns reveal how these aspects vary across the four principal approaches.

where:

• $M$: the number of graph connections per node (in HNSW)
• $C$: the centroid storage cost (in IVF)
• $K$: the number of clusters (in IVF)
• $d'$: the compressed dimension (in quantization methods)
• $n$: the number of vectors in the collection
• $d$: the dimensionality of the vector space

Several patterns in this table deserve attention. First, notice that exact search has $O(1)$ index build time, because there is no index to build: you simply store the raw vectors. All approximate methods require an upfront investment in index construction, whether that is building a graph (HNSW), clustering vectors into partitions (IVF), or learning codebooks (quantization). This build cost is amortized over all future queries, which makes it worthwhile when the collection will be queried many times.

Second, observe the memory column. Graph-based methods add $M$ connections per vector on top of the full vector storage, which increases memory usage but enables the fast navigable graph traversal that gives HNSW its speed advantage. IVF methods add a relatively modest centroid storage cost $C$ (proportional to the number of clusters, not the number of vectors). Quantization methods achieve the greatest memory savings by replacing the full $d$-dimensional vector with a compressed code of dimension $d'$, where $d'$ can be 8 to 32 times smaller than $d$.

The graph-based approach (HNSW) typically offers the best recall at a given query speed, which is why it has become the dominant ANN method. However, it uses more memory than quantization-based approaches because it stores both the full vectors and the graph edges.

FAISS (Facebook AI Similarity Search) is the most widely used library for vector similarity search. Developed by Meta AI, it provides efficient implementations of exact search, IVF, HNSW, PQ, and their combinations, with both CPU and GPU backends. Let's use it to compare exact and approximate search on a realistic dataset.

We will create a synthetic dataset that mimics the scale and dimensionality of a real embedding collection.

Our collection occupies about 146 MB, which is modest enough for exact search on a laptop. At 10x or 100x this scale, approximate methods become needed.

FAISS works by building an index object, adding vectors to it, and then calling search() to retrieve the top-k results. Different index types expose different trade-offs. IndexFlatIP is exact inner product search with no index overhead. IndexIVFFlat partitions the space into $K$ clusters and searches only nprobe of them. IndexHNSWFlat builds the navigable small-world graph. All three have the same add() and search() interface, which makes it easy to swap between them as your requirements change.

FAISS provides IndexFlatIP for exact inner product search and IndexFlatL2 for exact Euclidean distance search. Since our vectors are normalized, inner product is equivalent to cosine similarity.

The exact search returns the true nearest neighbors with cosine similarities. These results serve as our ground truth for evaluating approximate methods.

Notice that the similarity scores for nearest neighbors are typically in the range of 0.2-0.4 for random synthetic data, considerably lower than what you would see with real text embeddings. This is because random Gaussian vectors in high dimensions tend to be nearly orthogonal to each other by the curse of dimensionality. With real embeddings trained on meaningful text, similarity scores for relevant document pairs routinely reach 0.7-0.9.

The IVF (Inverted File) index partitions vectors into clusters, then only searches the clusters closest to the query. The nprobe parameter controls how many clusters to search: higher nprobe means higher recall but slower search.

A rule of thumb for choosing the number of clusters is $K \approx \sqrt{n}$ for good recall-speed balance. For 100,000 vectors, this suggests around 316 clusters. Using 100 here is slightly under this guideline, which is fine for demonstration.

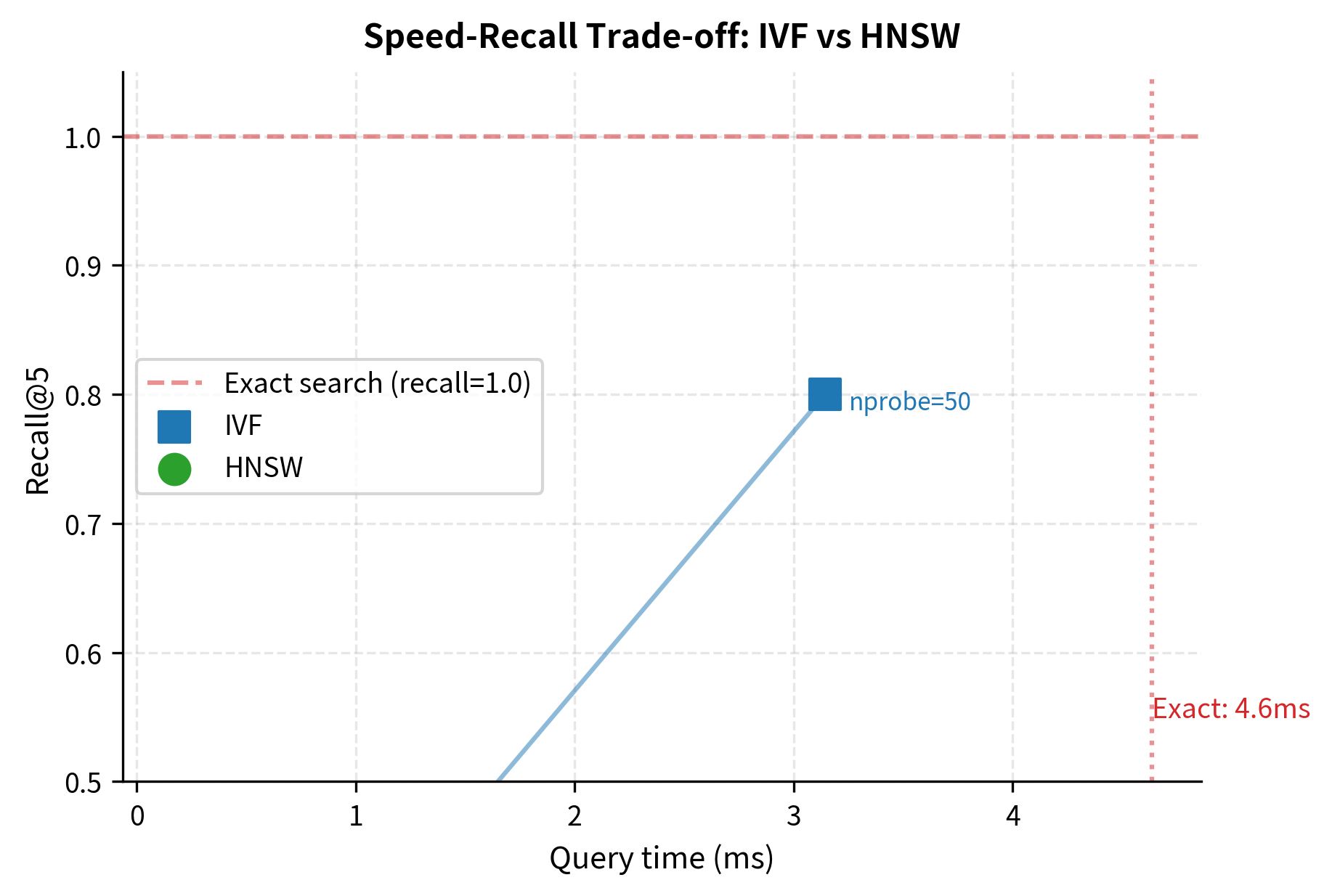
You can see the speed-accuracy trade-off in action. With nprobe=1 (searching only the single nearest cluster), the search is very fast but misses some true neighbors. As nprobe increases, recall improves but search time grows. At nprobe=50 (searching half of all clusters), recall is typically near perfect, but you are examining so many clusters that the speed advantage over exact search is diminishing. In production, you would choose nprobe based on your latency budget, typically achieving recall above 0.95 with nprobe around 5-20% of the total cluster count.

FAISS also provides an HNSW index, which builds a navigable graph structure. The key parameter is efSearch, which controls how many candidates to evaluate during the graph traversal. Higher values explore a broader region of the graph, improving recall at the cost of latency.

The M parameter (set during index construction) controls the number of neighbors each node connects to in the graph. Higher M values improve recall and search speed but increase both memory usage and index build time. Common values range from 16 to 64 for most applications.

HNSW generally achieves higher recall at lower latency than IVF for a given collection size, especially at moderate to high recall targets. The next chapter dives deep into exactly how the HNSW graph structure achieves this.

The plot shows the basic trade-off that defines ANN search. Each point represents a different parameter setting, and the goal is to get as close to the upper-left corner as possible (high recall, low latency). The curve connecting the points for each method is called the Pareto frontier: no operating point on that curve is dominated by another point (you cannot simultaneously improve both recall and speed without changing the index type). In practice, you would benchmark your specific collection and choose the operating point that balances your latency budget with your recall requirements.

The key parameters for the FAISS index implementations are:

• n_clusters: The number of clusters (Voronoi cells) to partition the vector space into for the IVF index. A common starting point is $K \approx \sqrt{n}$, where $n$ is the collection size.
• nprobe: The number of closest clusters to search during an IVF query. Higher values increase recall but reduce speed. Typical production values range from 5 to 50.
• M: The number of edges (neighbors) per node in the HNSW graph. Controls graph connectivity and memory usage. Values between 16 and 64 cover most use cases.
• efSearch: The size of the dynamic candidate list during HNSW search. Higher values improve recall at the cost of latency. Must be at least $k$ (the number of results requested).
• efConstruction: A build-time parameter for HNSW that controls the quality of the graph structure. Higher values produce better graphs but increase build time.

FAISS is the most established library, but the vector search ecosystem has grown rapidly. Here is a brief overview of the major options, grouped by their positioning in the stack.

These libraries provide the algorithmic primitives without a database layer:

FAISS (Meta) is the gold standard for research and production. It supports CPU and GPU, with extensive index types (Flat, IVF, HNSW, PQ, and combinations). Written in C++ with Python bindings, FAISS is the right choice when you need fine-grained control over index construction, when you need GPU acceleration, or when you are building a custom retrieval pipeline.

HNSWlib is a standalone C++ implementation of the HNSW algorithm with Python bindings. Lighter weight than FAISS, focused exclusively on HNSW. This is a good choice when you only need the HNSW index type and want minimal dependencies. It is especially popular for embedding-based retrieval in NLP research because of its simplicity and good performance.

Annoy (Spotify) uses random projection trees. Its key advantage is memory mapping: you can build an index, save it to disk, and then load it into multiple processes simultaneously without duplicating the memory footprint. This makes it attractive for applications that share a single index across many parallel workers. The main limitation is that Annoy does not support adding vectors after index construction, requiring a full rebuild when the collection changes.

ScaNN (Google) is optimized for inner product search with a technique called anisotropic vector quantization, which learns quantization codebooks that minimize the directional error relevant to retrieval rather than the absolute reconstruction error. ScaNN achieves state-of-the-art speed-recall trade-offs on several standard benchmarks. It is the right choice for production systems that have benchmarked multiple options and need the absolute best performance.

Vector databases add persistence, filtering, distributed search, and managed infrastructure on top of the core ANN algorithms:

Qdrant is an open-source vector database written in Rust, known for its support of rich payload filtering (combining vector search with structured metadata constraints), on-disk indexing for large collections that exceed RAM, and support for multiple vector types per document (dense, sparse, and named vectors).

Milvus is an open-source distributed vector database designed for billion-scale collections. It separates storage, compute, and coordination into distinct layers, letting horizontal scaling of each component independently. Milvus supports a wider range of index types than most alternatives, including GPU acceleration.

Weaviate emphasizes semantic search with built-in module support for generating embeddings from text or images, which makes it easy to set up a pipeline without managing embedding models separately. It also supports hybrid search that combines vector and keyword search natively.

Pinecone is a managed vector database service that eliminates operational overhead at the cost of vendor lock-in. It manages the infrastructure and scaling, including service updates. Pinecone is a reasonable choice for teams that want to move quickly without managing distributed systems.

The choice between a library and a database depends on your requirements. For a RAG system where the document collection fits in memory and you control the embedding pipeline, FAISS or HNSWlib provides maximum flexibility and performance. For a production system requiring persistence, real-time updates, metadata filtering, and operational monitoring, a vector database handles concerns that libraries leave to you.

A pragmatic framework for choosing:

1. Start with FAISS if you are prototyping or building a custom pipeline and your collection fits in memory. It gives you the most control and is well-documented.
2. Switch to HNSWlib if you only need HNSW and want simpler code.
3. Consider Qdrant or Weaviate if you need metadata filtering ("find documents similar to this query and tagged with topic=finance") or operational features like monitoring and backup.
4. Use Pinecone or a cloud-native solution if minimizing operational burden is more important than cost or performance optimization.

Vector similarity search is powerful but comes with important caveats that affect real-world RAG systems.

A key limitation is that vector similarity is not semantic equivalence. Two documents can have high cosine similarity without being relevant to the query, and relevant documents can sometimes have lower similarity scores than irrelevant ones. This happens because embedding models compress complex, fine-grained meaning into fixed-size vectors, and information is inevitably lost in this compression.

A query about "python programming" might retrieve documents about actual pythons if the embedding model does not sufficiently distinguish context. This is one reason why RAG pipelines typically include a reranking stage (covered later in this part), which uses a more expensive cross-encoder model to rescore the top candidates. The reranker examines the full query-document pair jointly, capturing cross-document context that a bi-encoder embedding model cannot represent. This two-stage pipeline, retrieve then rerank, is the standard architecture for production RAG.

The severity of the semantic gap depends on the quality and training data of the embedding model. A general-purpose embedding model trained on diverse web text will struggle with specialized technical domains where terminology overlaps with everyday language. Domain-specific fine-tuning of embedding models is one of the most effective ways to close this gap, and this is covered in the chapter on fine-tuning for retrieval.

The curse of dimensionality affects ANN algorithms in subtle but important ways. In very high-dimensional spaces, the ratio between the nearest and farthest neighbor distances shrinks. As $d$ grows, all pairwise distances converge toward the same value, which makes it increasingly difficult to distinguish between near and far neighbors.

This effect is most pronounced in uniformly distributed random data. Typical embedding dimensions (384-1536) are high enough that this effect is noticeable but not catastrophic. However, it means that ANN algorithms cannot offer the same theoretical guarantees in high dimensions that they can in low dimensions. In practice, the learned structure of real embeddings, which cluster by topic and style rather than being uniformly distributed, counteracts this effect, and ANN methods work much better on real data than worst-case theory would suggest.

The anisotropy of text embeddings, where vectors cluster in a narrow cone of the high-dimensional space rather than filling it uniformly, is both a curse and a blessing for search. It means that random pairs tend to have non-trivially positive cosine similarity (the curse), which makes it harder to distinguish relevant from irrelevant documents. But it also means that the clustering structure that ANN algorithms exploit is more pronounced, so cluster-based methods like IVF work particularly well.

Memory remains a persistent practical concern. Storing 100 million 768-dimensional vectors in float32 requires about 288 GB of RAM, before accounting for the additional memory needed by the index structure itself (graph edges for HNSW, centroid tables for IVF, etc.). Few single machines can accommodate this.

Product Quantization and other compression techniques, which we cover in a dedicated chapter, can reduce this by 10-30x, but at the cost of reduced recall. A production RAG system must meet its accuracy target within a fixed memory and latency budget. A common production architecture uses PQ for initial candidate retrieval (fast, memory-efficient, moderate recall), followed by re-scoring with the full float32 vectors for the top candidates (slower, exact, but applied only to a small candidate set).

The float16 quantization of vector components, which reduces the per-vector memory by 2x with negligible impact on retrieval quality, is also widely used. Modern embedding models are trained with float32 precision, but the stored vectors can be safely quantized to float16 for retrieval purposes without significant recall degradation.

Vector search indexes are generally static or semi-static. While some structures (like HNSW) support incremental insertion, most achieve their best performance when built once on the full dataset. Frequent updates, such as adding or deleting documents in real time, can degrade index quality or require expensive rebuilds.

HNSW supports efficient incremental insertion: new vectors are connected into the graph during insertion without requiring a global rebuild. However, there is no efficient deletion mechanism: deleting a vector leaves "tombstoned" nodes in the graph that continue to be examined during search, wasting computation. The standard workaround is periodic full rebuilds combined with a "soft delete" approach that filters out deleted documents in post-processing.

IVF indices are more sensitive to distributional shift. If new documents are added that fall outside the existing cluster regions, the cluster assignments become suboptimal and recall degrades. Periodic retraining and rebuilding of the cluster centroids is typically necessary when the document distribution evolves significantly.

Tiered architectures address the update problem by combining a large static index (rebuilt periodically) with a small dynamic index (maintained in real time, queried with exact search due to its small size). New documents are added to the dynamic tier and periodically merged into the static tier during off-peak hours. This approach is used by large-scale production systems where both update velocity and query latency are important.

A subtle but important failure mode is metric mismatch: using a search metric that does not match the metric used during embedding model training. Many practitioners default to cosine similarity without checking whether their chosen embedding model was trained with cosine, dot product, or Euclidean distance. While the difference is often small after normalization (since normalized dot product equals cosine similarity), models trained with dot product and unconstrained vector norms may use magnitude as a meaningful signal. Using cosine similarity with such a model discards this signal.

Always read the embedding model documentation to understand the intended search metric. When in doubt, normalize your vectors: this makes the choice of metric moot and avoids metric mismatch problems regardless of how the model was trained.

This chapter established the foundations of vector similarity search, the core retrieval operation in any RAG pipeline.

Distance metrics define what "similar" means in vector space. Cosine similarity (direction-based) is the default for text embeddings, while dot product is equivalent for normalized vectors and Euclidean distance captures position-based proximity. Always match your search metric to your embedding model's training objective. For normalized vectors, all three metrics induce identical rankings, which is why pre-normalizing at index time is standard practice.

Exact search computes distances against every vector in the collection, guaranteeing perfect recall at $O(n \cdot d)$ cost per query. It is practical for small collections (under roughly 1 million vectors on CPU, or more with GPU batching) but does not scale. Its main role is as a ground-truth generator for evaluating ANN recall.

Approximate Nearest Neighbor (ANN) algorithms achieve sublinear query time by sacrificing a small, controllable amount of recall. The key families are tree-based (efficient in low dimensions, but limited in high dimensions), hash-based (LSH, simple and parallelizable but memory-intensive), graph-based (HNSW, currently dominant due to excellent recall-speed balance), partition-based (IVF, good for very large collections), and compression-based (Product Quantization, for memory-constrained settings).

FAISS is the most widely used similarity search library. This provides implementations of all major index types with both CPU and GPU backends. The recall-vs-speed trade-off curves we generated show how parameter tuning lets you find the right operating point for your application. Libraries like HNSWlib, Annoy, and ScaNN offer specialized alternatives, while vector databases like Qdrant and Milvus add persistence and operational features for production deployments.

The limitations of vector search (semantic gap, curse of dimensionality, memory constraints, update costs) motivate the full RAG pipeline architecture, where approximate retrieval feeds into reranking and other refinement stages that compensate for the inherent approximations of embedding-based search.

With the conceptual framework and metrics in place, the next three chapters examine the specific index structures that make large-scale ANN search possible: HNSW graphs, IVF partitioning, and Product Quantization.

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about vector similarity search.