WritingBooksAboutCommunityContactCommunity

Confidence Intervals and Test Assumptions

Michael Brenndoerfer•Updated January 12, 2026•23 min read

Mathematical equivalence between confidence intervals and hypothesis tests, test assumptions (independence, normality, equal variances), and choosing between z and t tests. Learn how to validate assumptions and select appropriate tests.

Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Confidence Intervals and Test Assumptions

In the previous chapter, we established the foundations of hypothesis testing: p-values, null and alternative hypotheses, and test statistics. Now we explore two complementary concepts that complete your understanding of statistical inference.

First, we'll discover that confidence intervals and hypothesis tests are mathematically equivalent. They're not two different methods for analyzing data; they're two perspectives on the same underlying calculation. Understanding this equivalence transforms how you interpret both tools.

Second, we'll examine the assumptions that make statistical tests work. Every test rests on mathematical assumptions, and when these assumptions are violated, tests can mislead you. Knowing what assumptions matter, when they matter, and what to do when they fail is essential for responsible data analysis.

Confidence Intervals: A Deeper Look

You've probably seen confidence intervals before: "The average treatment effect was 5.2 with a 95% confidence interval of [3.1, 7.3]." But what does this actually mean, and how does it connect to hypothesis testing?

What a Confidence Interval Really Means

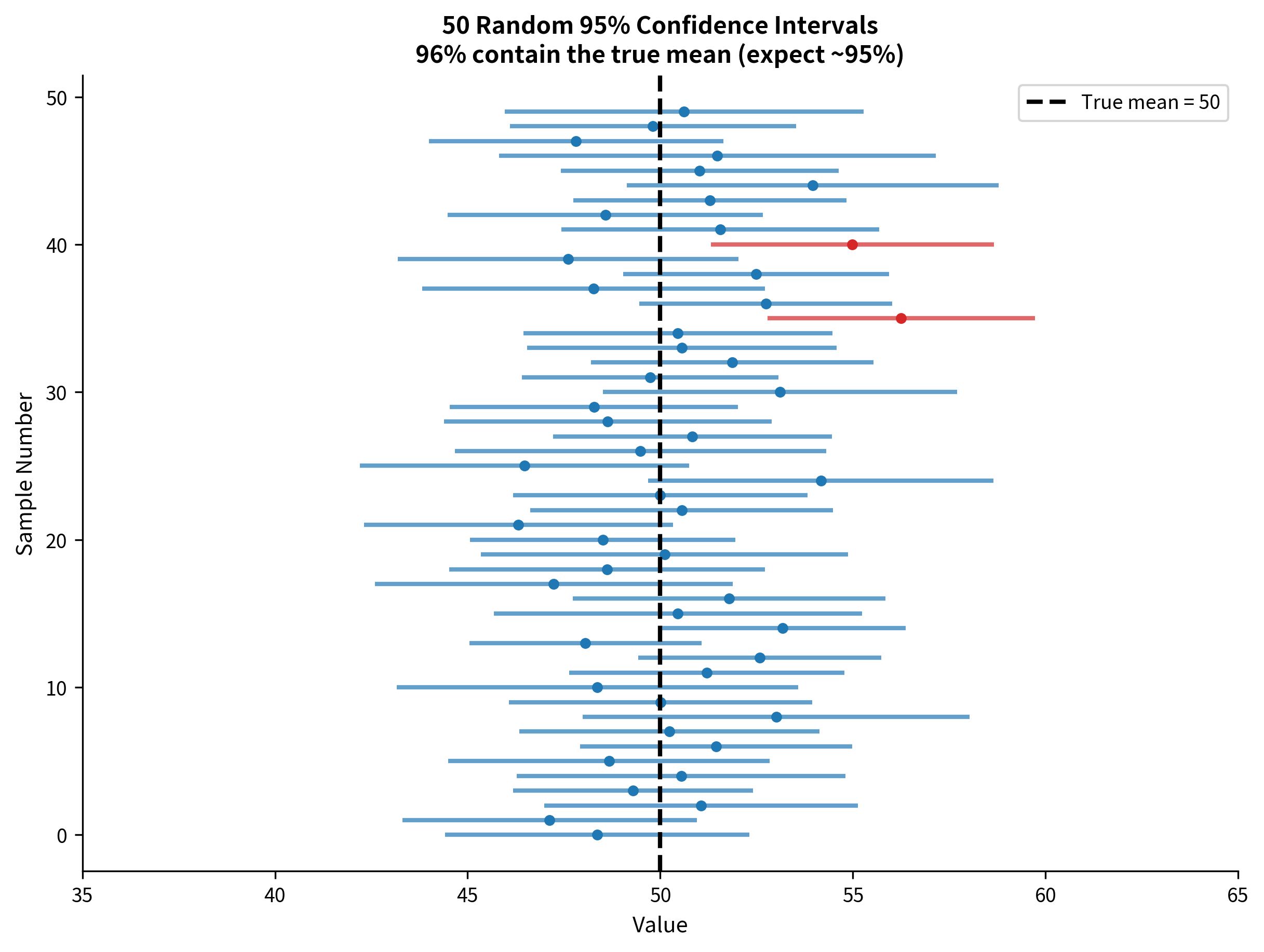
A 95% confidence interval does NOT mean there's a 95% probability that the true parameter lies within the interval. The true parameter is fixed (though unknown). It's either inside the interval or it isn't. There's no probability involved once you've computed the interval.

Confidence Interval Interpretation

A 95% confidence interval means: if we repeated our sampling procedure many times and computed a confidence interval each time, 95% of those intervals would contain the true parameter value.

This is a subtle but important distinction. The confidence refers to the procedure, not to any particular interval. Over many repetitions, 95% of the intervals produced by this method will capture the true value.

Out[2]:
Visualization
Multiple horizontal confidence intervals with most containing the true population mean marked by a vertical line.
Simulation showing what '95% confidence' actually means. Each horizontal line represents a 95% confidence interval from a different random sample of the same population (true mean = 50). About 95% of intervals (blue) contain the true mean, while about 5% (red) miss it. The randomness is in which samples we happen to draw, not in the parameter itself.

Constructing a Confidence Interval Step by Step

Let's build a confidence interval from first principles. Suppose you have a sample of n observations and want a (1−α)×100%(1-\alpha) \times 100\% confidence interval for the population mean.

Step 1: Calculate the sample mean

xˉ=1n∑i=1nxi\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i

Step 2: Calculate the standard error

The standard error measures how much the sample mean varies from sample to sample. If you know the population standard deviation σ\sigma:

SE=σnSE = \frac{\sigma}{\sqrt{n}}

If you don't know σ\sigma (the usual case), estimate it with the sample standard deviation:

SE=snwheres=1n−1∑i=1n(xi−xˉ)2SE = \frac{s}{\sqrt{n}} \quad \text{where} \quad s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2}

Step 3: Find the critical value

For a 95% confidence interval (α=0.05\alpha = 0.05), you need the value that cuts off 2.5% in each tail of the distribution.

If you know σ\sigma, use the z critical value: z1−α/2=z0.975=1.96z_{1-\alpha/2} = z_{0.975} = 1.96

If you're estimating σ\sigma with ss, use the t critical value with n−1n-1 degrees of freedom: t1−α/2,n−1t_{1-\alpha/2, n-1}

Step 4: Construct the interval

CI=xˉ±t1−α/2,n−1×SE=[xˉ−t1−α/2,n−1⋅sn,xˉ+t1−α/2,n−1⋅sn]\text{CI} = \bar{x} \pm t_{1-\alpha/2, n-1} \times SE = \left[\bar{x} - t_{1-\alpha/2, n-1} \cdot \frac{s}{\sqrt{n}}, \quad \bar{x} + t_{1-\alpha/2, n-1} \cdot \frac{s}{\sqrt{n}}\right]
In[3]:
Code
import numpy as np
from scipy import stats

# Sample data: reaction times in milliseconds
reaction_times = np.array(
    [
        245,
        268,
        252,
        241,
        259,
        263,
        248,
        271,
        255,
        249,
        262,
        247,
        258,
        244,
        266,
        253,
        260,
        242,
        257,
        251,
    ]
)

# Step 1: Sample mean
n = len(reaction_times)
sample_mean = np.mean(reaction_times)

# Step 2: Standard error
sample_std = np.std(reaction_times, ddof=1)
standard_error = sample_std / np.sqrt(n)

# Step 3: Critical value for 95% CI
alpha = 0.05
t_critical = stats.t.ppf(1 - alpha / 2, df=n - 1)

# Step 4: Construct the interval
margin_of_error = t_critical * standard_error
ci_lower = sample_mean - margin_of_error
ci_upper = sample_mean + margin_of_error

print(f"Sample size: n = {n}")
print(f"Sample mean: x̄ = {sample_mean:.2f} ms")
print(f"Sample std: s = {sample_std:.2f} ms")
print(f"Standard error: SE = {standard_error:.2f} ms")
print(f"t critical value (df={n - 1}): t = {t_critical:.3f}")
print(f"Margin of error: {margin_of_error:.2f} ms")
print(f"\n95% Confidence Interval: [{ci_lower:.2f}, {ci_upper:.2f}] ms")
Out[3]:
Console
Sample size: n = 20
Sample mean: x̄ = 254.55 ms
Sample std: s = 8.80 ms
Standard error: SE = 1.97 ms
t critical value (df=19): t = 2.093
Margin of error: 4.12 ms

95% Confidence Interval: [250.43, 258.67] ms

The Remarkable Equivalence

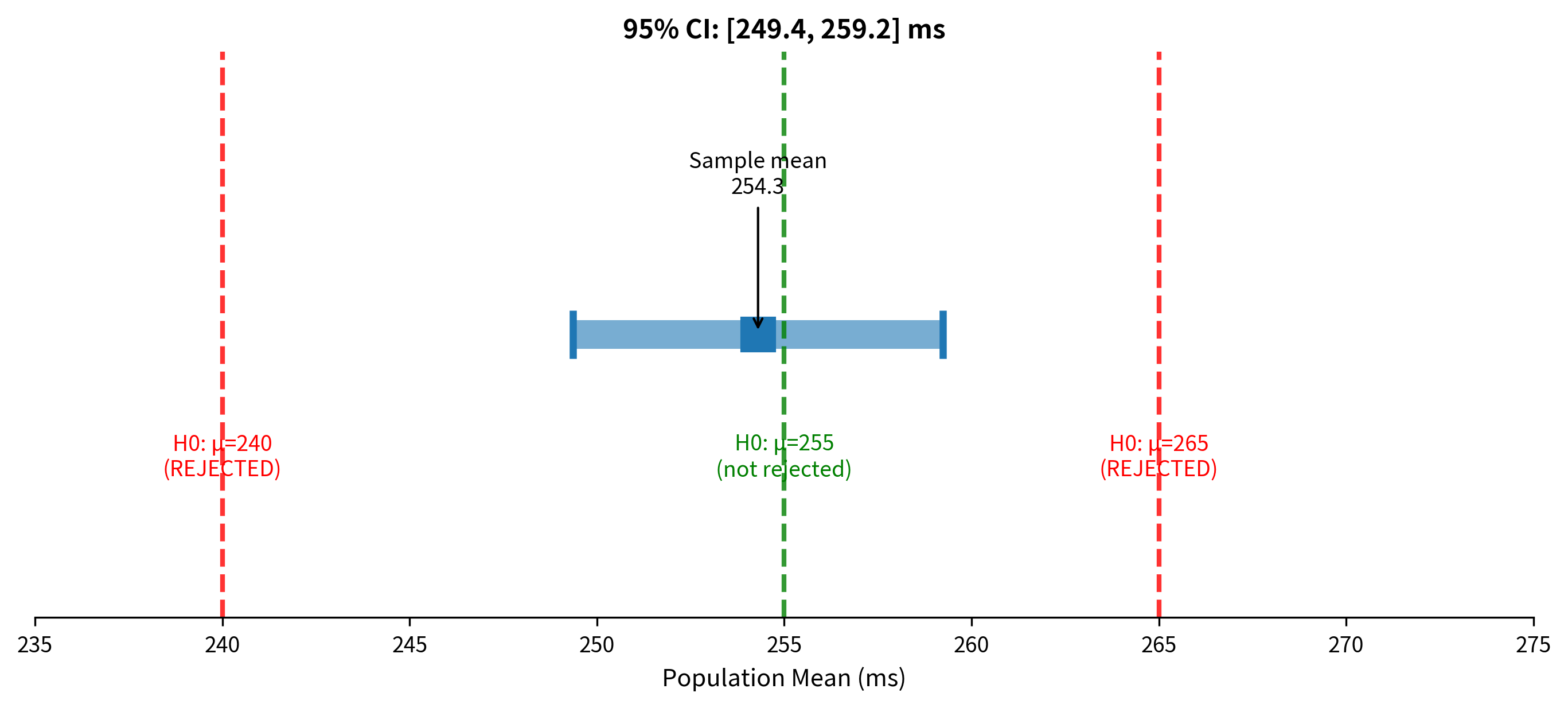
Here's the key insight that connects confidence intervals to hypothesis testing: a 95% confidence interval contains exactly those parameter values that would NOT be rejected by a two-sided hypothesis test at the 0.05 significance level.

Why the Equivalence Holds

Let's prove this algebraically. Consider testing H0:μ=μ0H_0: \mu = \mu_0 versus H1:μ≠μ0H_1: \mu \neq \mu_0 at significance level α=0.05\alpha = 0.05.

We reject H0H_0 when the test statistic exceeds the critical value:

∣xˉ−μ0SE∣>t0.975,n−1\left| \frac{\bar{x} - \mu_0}{SE} \right| > t_{0.975, n-1}

Rearranging this inequality:

∣xˉ−μ0SE∣>t0.975  ⟺  ∣xˉ−μ0∣>t0.975⋅SE  ⟺  xˉ−μ0>t0.975⋅SEORxˉ−μ0<−t0.975⋅SE  ⟺  μ0<xˉ−t0.975⋅SEORμ0>xˉ+t0.975⋅SE\begin{aligned} \left| \frac{\bar{x} - \mu_0}{SE} \right| > t_{0.975} &\iff |\bar{x} - \mu_0| > t_{0.975} \cdot SE \\ &\iff \bar{x} - \mu_0 > t_{0.975} \cdot SE \quad \text{OR} \quad \bar{x} - \mu_0 < -t_{0.975} \cdot SE \\ &\iff \mu_0 < \bar{x} - t_{0.975} \cdot SE \quad \text{OR} \quad \mu_0 > \bar{x} + t_{0.975} \cdot SE \end{aligned}

The last line says: we reject H0H_0 when μ0\mu_0 falls outside the interval [xˉ−t0.975⋅SE,xˉ+t0.975⋅SE][\bar{x} - t_{0.975} \cdot SE, \bar{x} + t_{0.975} \cdot SE].

But this interval is exactly the 95% confidence interval! So:

  • μ0\mu_0 inside the CI ⇒\Rightarrow hypothesis test fails to reject H0H_0
  • μ0\mu_0 outside the CI ⇒\Rightarrow hypothesis test rejects H0H_0

The confidence interval is the set of all parameter values that would not be rejected as null hypotheses.

Visualizing the Equivalence

Out[4]:
Visualization
Number line showing confidence interval with examples of rejected and non-rejected hypothesis values.
The equivalence between confidence intervals and hypothesis tests. The 95% CI is shown as the blue bar. Any hypothesized value inside the interval (like μ₀ = 255) would not be rejected. Any value outside (like μ₀ = 240 or μ₀ = 265) would be rejected. The CI simultaneously shows you the result of testing every possible null hypothesis.

Why This Matters Practically

This equivalence has important practical implications:

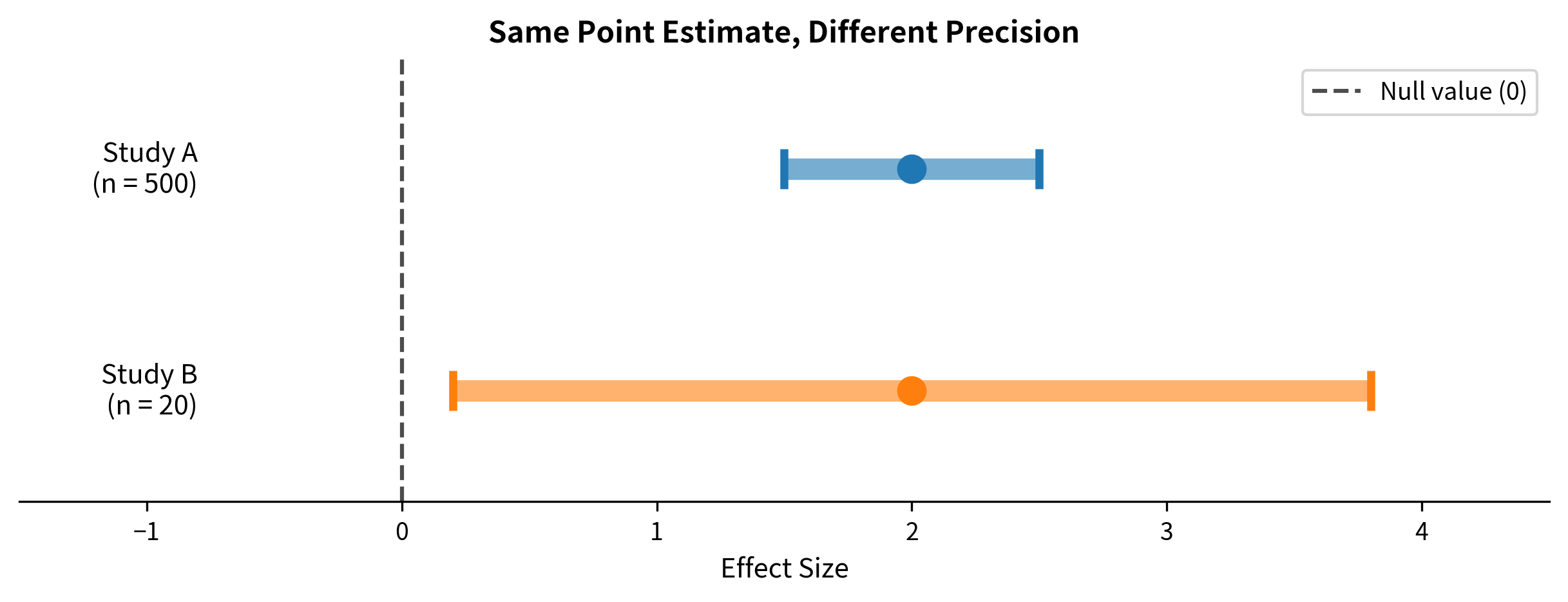
  1. Confidence intervals are more informative than p-values. A p-value tells you whether one specific null hypothesis is rejected. A confidence interval tells you which values would be rejected and which wouldn't. It's like the difference between asking "Is the speed limit 65 mph?" versus "What range of speed limits are consistent with my speedometer reading?"

  2. You can read significance from a CI. If a 95% CI for a difference doesn't include zero, the difference is significant at the 0.05 level. If the CI for a ratio doesn't include 1, the ratio is significant. You don't need to compute a separate test.

  3. CIs convey precision. A CI of [0.1, 0.3] and a CI of [-2, 5] might both exclude zero (both "significant"), but the first shows you know the effect is small and positive, while the second shows you barely know anything at all.

Out[5]:
Visualization
Two horizontal confidence intervals with different widths but the same center point.
Two studies with the same point estimate (effect = 2) but different precision. Study A has a narrow CI, providing strong evidence the effect is between 1.5 and 2.5. Study B has a wide CI, suggesting high uncertainty about the true effect size. Both CIs exclude zero, so both are 'statistically significant,' but they convey very different information.

Test Assumptions: The Foundation of Valid Inference

Every statistical test is built on assumptions. When these assumptions hold, the test does what it claims: it controls the Type I error rate at the specified level and has known power properties. When assumptions are violated, these guarantees may break down.

Understanding assumptions isn't about rigidly checking boxes. It's about understanding when violations matter, when they don't, and what alternatives exist.

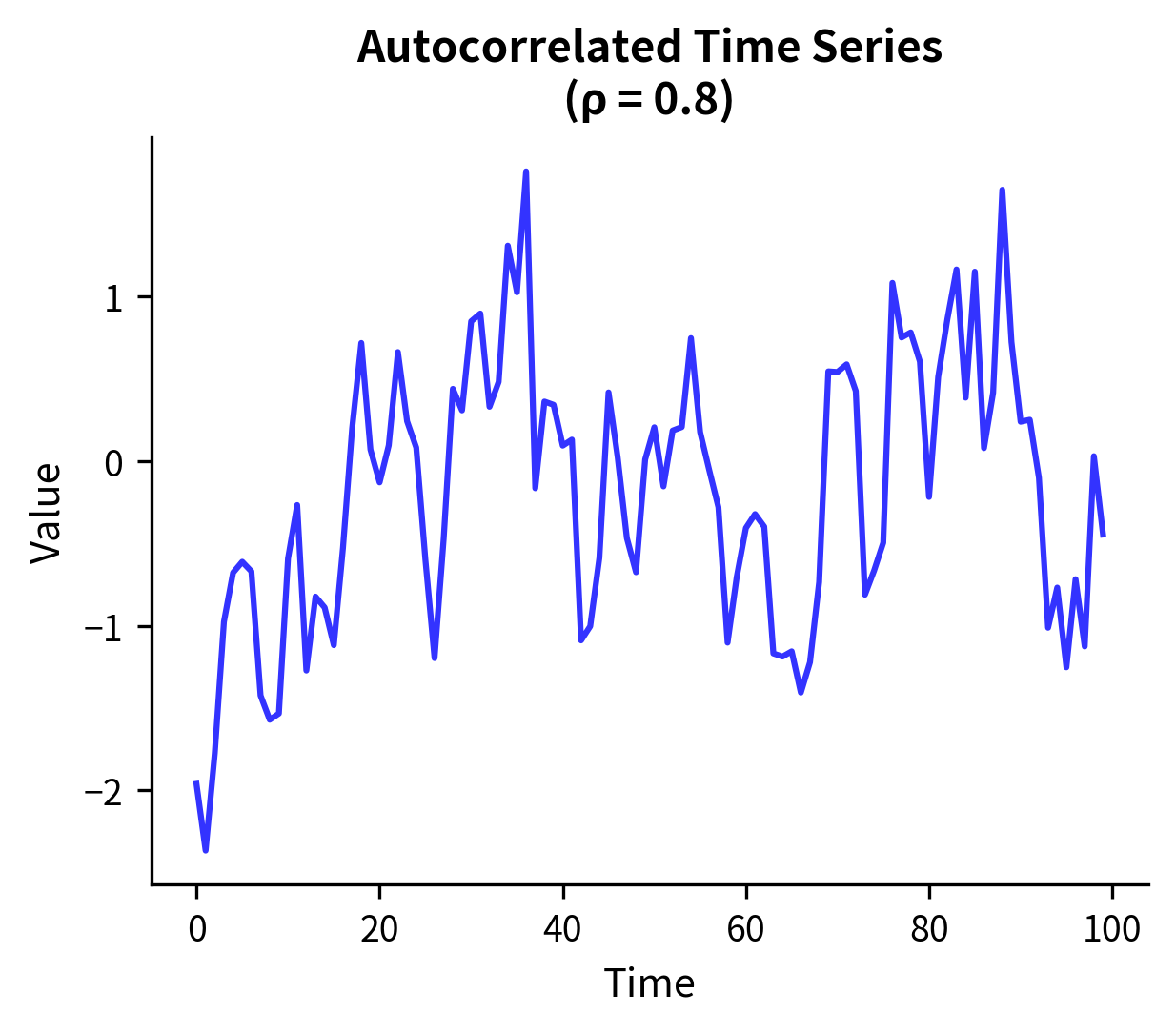
Assumption 1: Independence

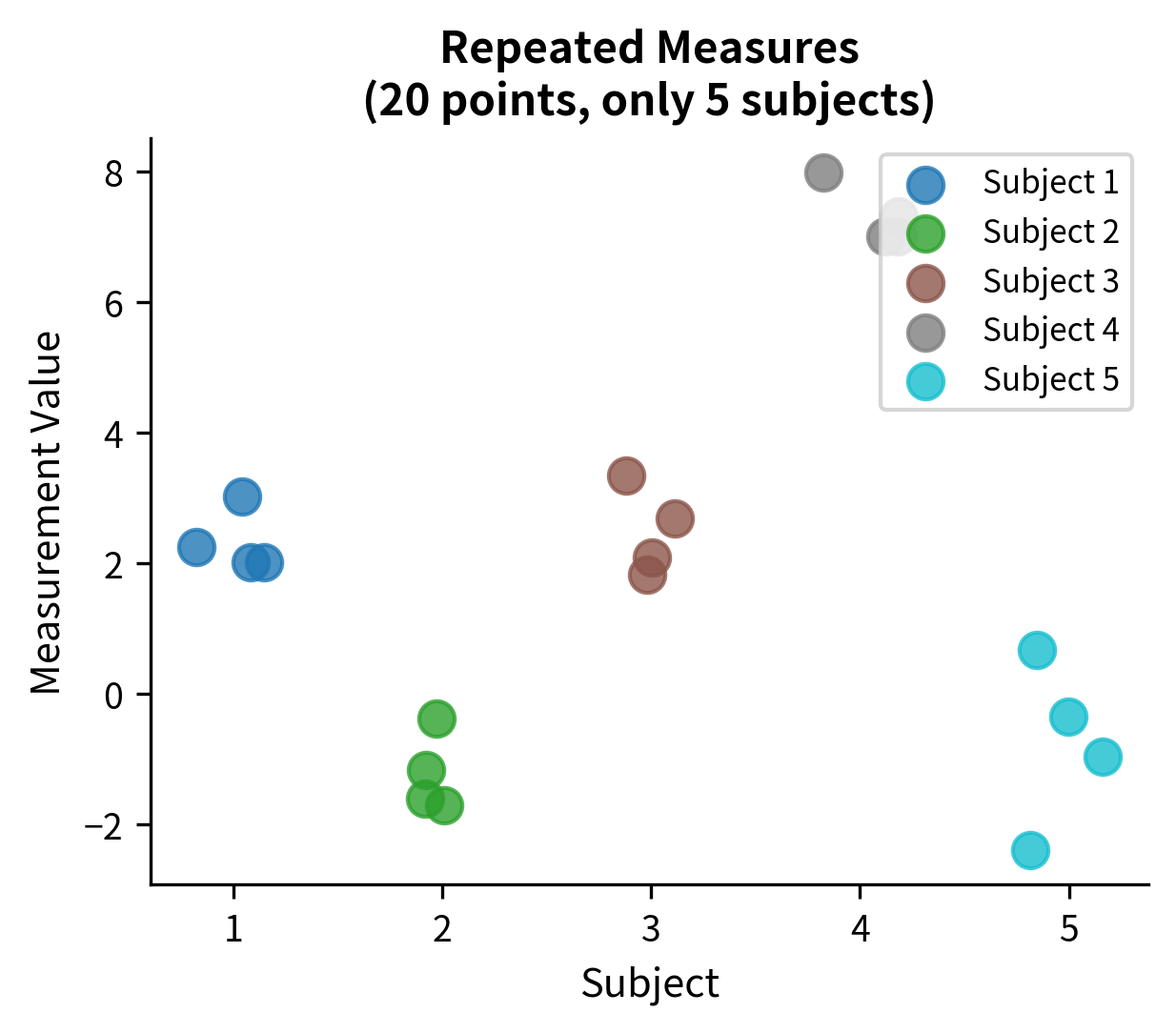
Independence is the most important assumption and the one most commonly violated without recognition.

What independence means: Each observation provides unique information. The value of one observation doesn't tell you anything about another observation's value.

Why it matters: Statistical tests calculate standard errors assuming each observation contributes independent information. When observations are correlated, the effective sample size is smaller than the actual sample size. The test "thinks" it has more information than it does, leading to standard errors that are too small, test statistics that are too large, and p-values that are too small.

Common violations:

Out[6]:
Visualization
Scatter plot showing repeated measures from 5 subjects with clear within-subject correlation.
Repeated measures: Multiple measurements from the same subjects are correlated. If Subject 1 has high values, all their measurements tend to be high. The 20 points come from only 5 independent subjects.
Line plot showing autocorrelated time series data.
Time series: Sequential observations are autocorrelated. Today''s value is related to yesterday''s. The 100 points do not represent 100 independent pieces of information.

The consequences: If you analyze repeated measures as if they were independent, your standard errors will be too small (often dramatically so), your p-values will be too small, and you'll make many more false positive claims than you think. A study that appears to have n=100 might effectively have n=10 if each of 10 subjects contributes 10 correlated measurements.

Solutions: Use methods designed for your data structure:

  • Repeated measures: paired t-tests, repeated measures ANOVA, mixed-effects models
  • Clustered data: cluster-robust standard errors, mixed-effects models
  • Time series: ARIMA models, autocorrelation-corrected standard errors

Assumption 2: Normality

Many tests assume the data (or the sampling distribution of a statistic) is normally distributed.

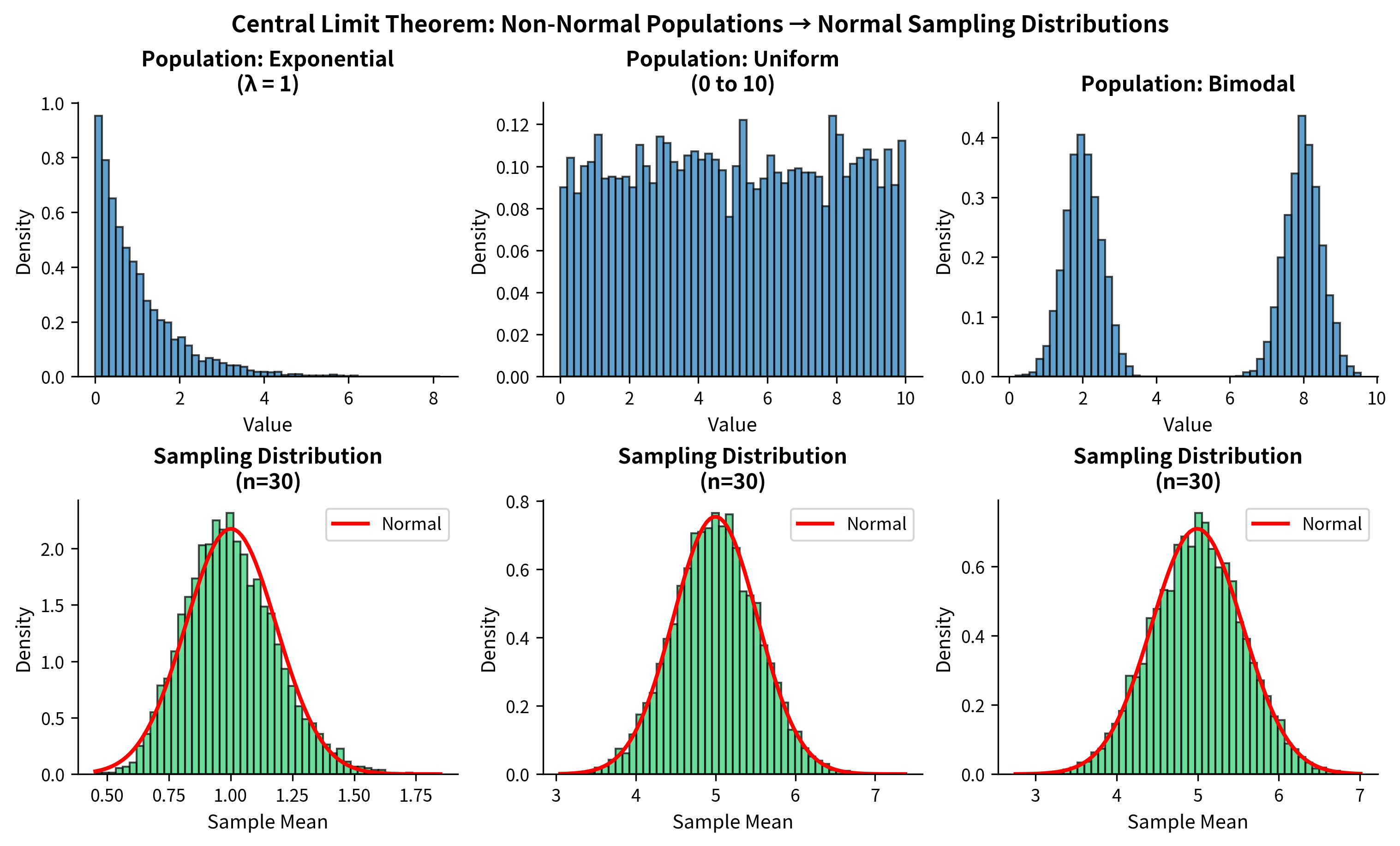
What normality means: The t-test and z-test assume that the sampling distribution of the mean is normal. For small samples, this requires the population itself to be approximately normal. For large samples, the Central Limit Theorem saves us.

The Central Limit Theorem: This remarkable theorem states that the sampling distribution of the mean approaches normality as sample size increases, regardless of the population distribution. This is why t-tests work even when individual observations aren't normal.

Out[7]:
Visualization
Six histograms arranged in two rows showing population distributions and their corresponding sampling distributions of the mean.
The Central Limit Theorem in action. The top row shows three very different population distributions (exponential, uniform, and bimodal). The bottom row shows the sampling distribution of the mean for samples of n=30 from each population. Despite the non-normal populations, the sampling distributions are approximately normal.

How fast does the CLT work? It depends on the population distribution:

Population DistributionSample Size Needed for Approximate Normality
Already normalAny n works
Symmetric, light tailsn ≥ 10 usually sufficient
Moderately skewedn ≥ 30 is a common guideline
Heavily skewedn ≥ 50 to 100 may be needed
Very heavy tailsn ≥ 100+ may be needed

When normality matters most: For small samples (n < 20 or so), the shape of the population distribution affects test validity. Severe skewness or outliers can inflate or deflate Type I error rates.

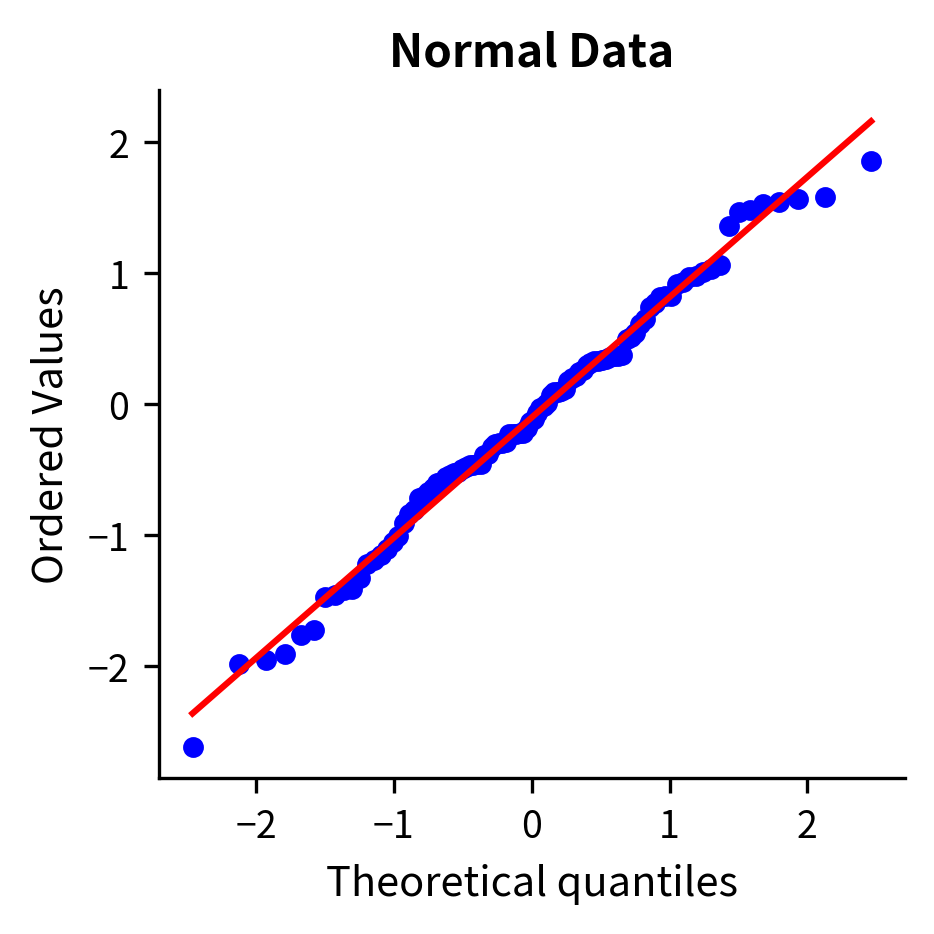
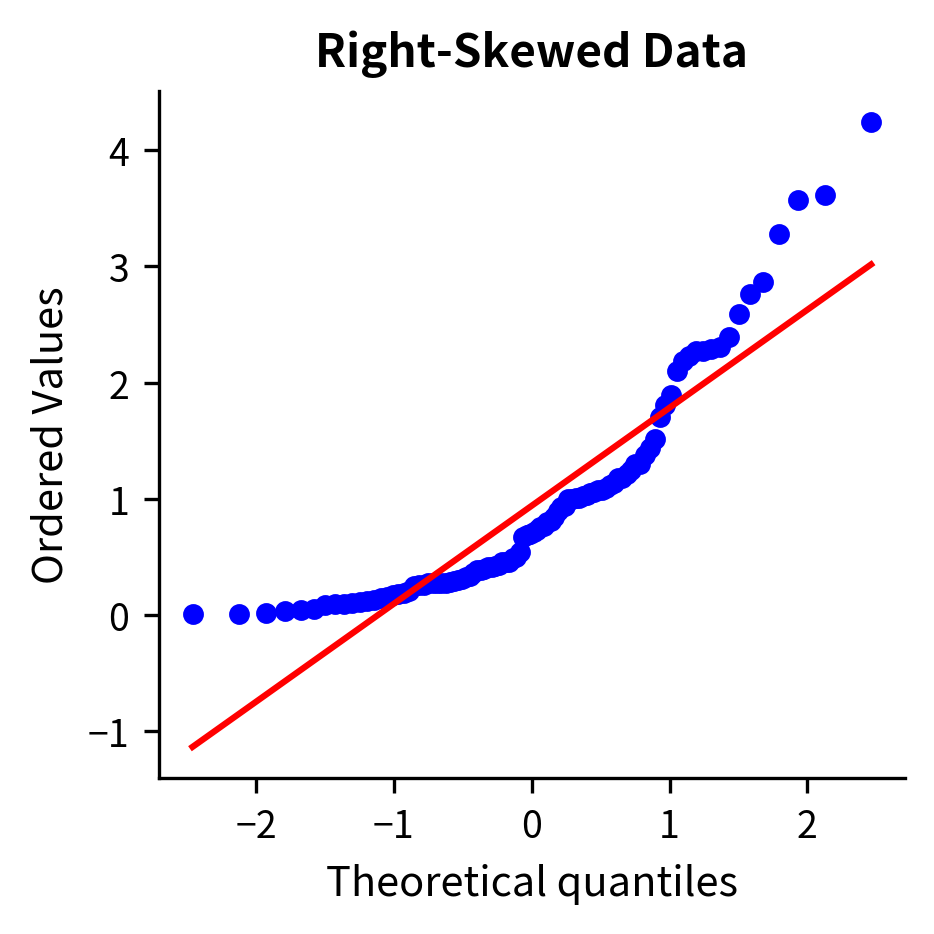
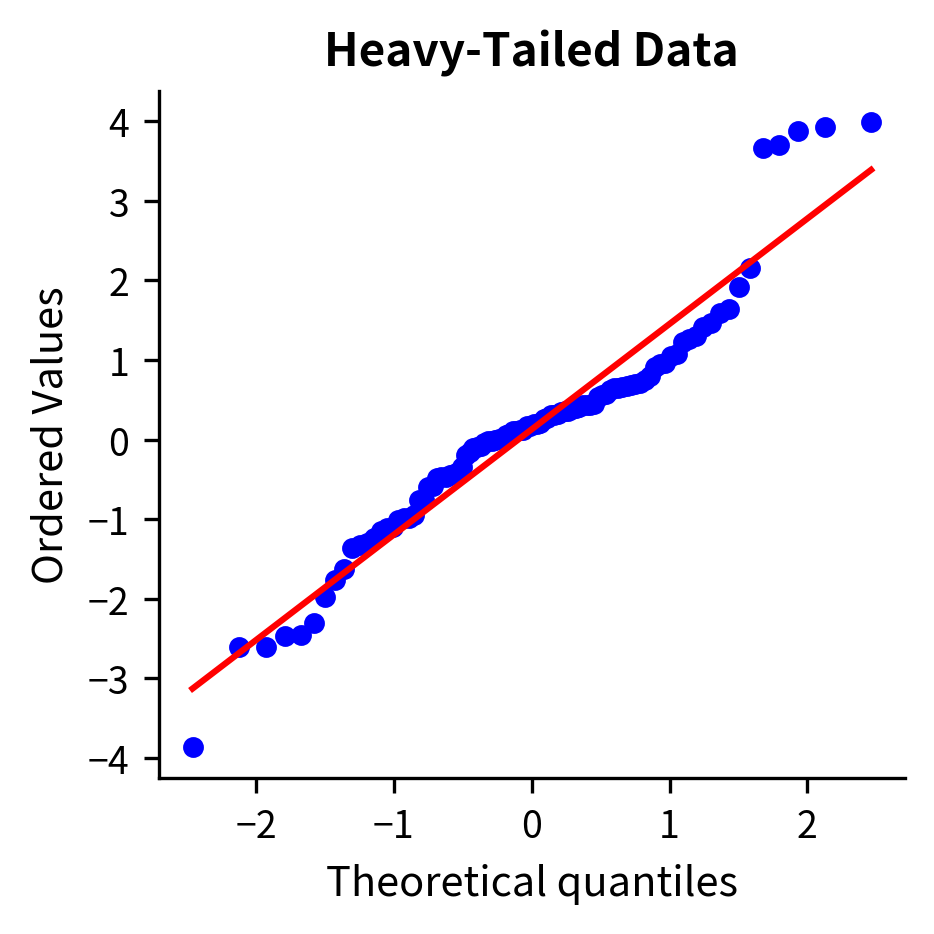
Checking normality: Use histograms and Q-Q plots to visually assess normality. Q-Q plots compare your data quantiles to theoretical normal quantiles. Points should fall roughly on a straight line if the data are normal.

Out[8]:
Visualization
Q-Q plot showing points along diagonal line for normal data.
Q-Q plot for normal data: Points fall along the diagonal line, indicating the data are approximately normally distributed.
Q-Q plot showing curved pattern for skewed data.
Q-Q plot for right-skewed data: Points curve upward at the right end, indicating a right (positive) skew with heavier right tail than normal.
Q-Q plot showing S-shaped pattern for heavy-tailed data.
Q-Q plot for heavy-tailed data: Points curve away from the line at both ends, indicating heavier tails than the normal distribution.

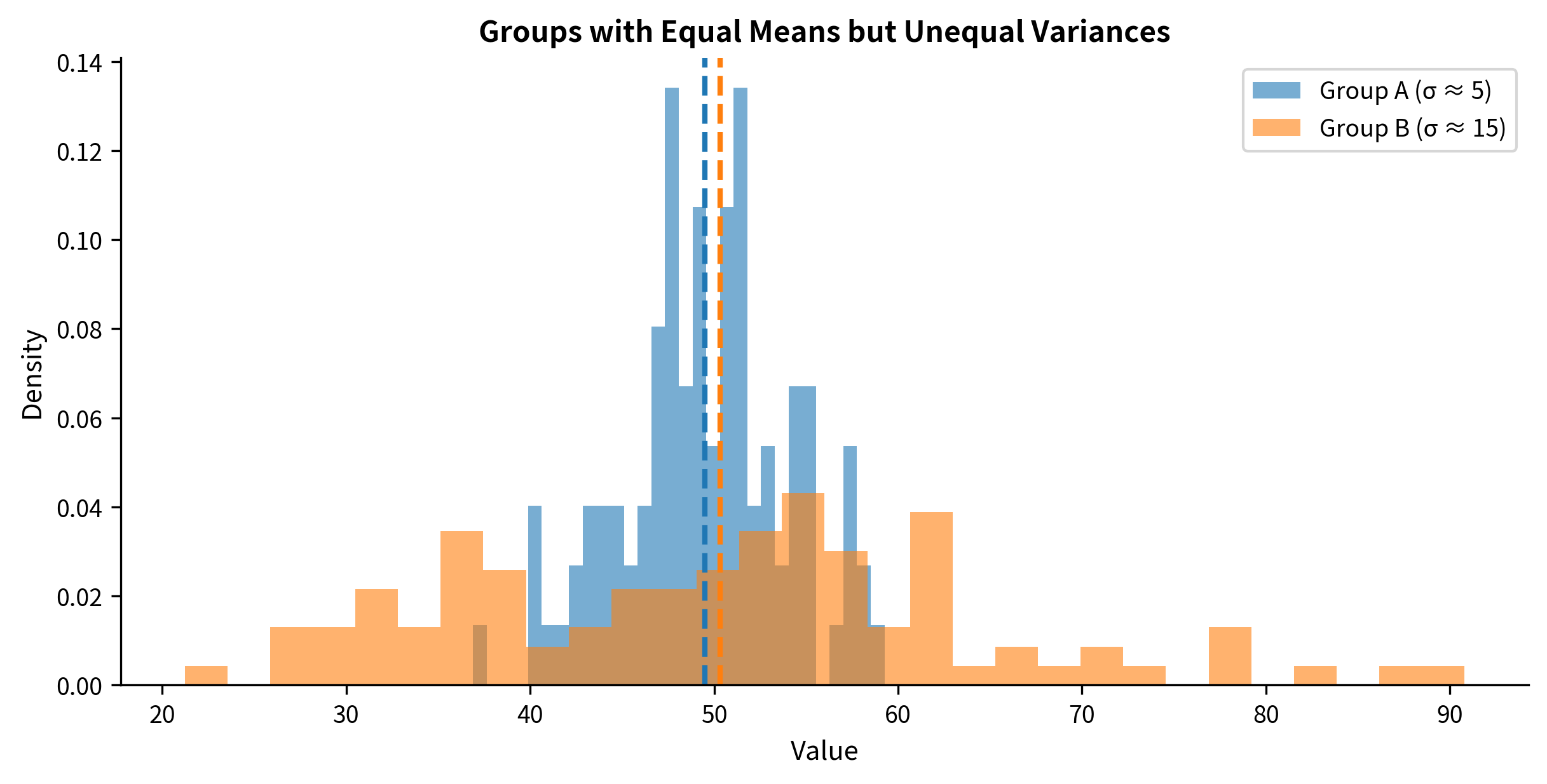
Assumption 3: Equal Variances (Homoscedasticity)

Two-sample t-tests can assume equal variances in both groups (pooled t-test) or allow unequal variances (Welch's t-test).

Why equal variances matter for the pooled test: The pooled t-test combines variance estimates from both groups to get a single "pooled" variance:

sp2=(n1−1)s12+(n2−1)s22n1+n2−2s_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}

This pooling is only valid if both groups truly have the same variance. When variances differ, the pooled estimate doesn't accurately represent either group.

What happens when variances differ: The consequences depend on the relationship between variance and sample size:

  • If the group with larger variance has smaller n: Type I error is inflated (you reject too often)
  • If the group with larger variance has larger n: Type I error is deflated (you reject too rarely)
  • If sample sizes are equal: Effects are minimal
Out[9]:
Visualization
Two overlapping histograms showing groups with different variances.
The problem with unequal variances. When Group B has higher variance (shown by wider spread), the pooled variance estimate is a compromise that doesn't accurately represent either group. The standard error of the difference is incorrectly calculated, leading to biased inference.

The solution: Welch's t-test: Welch's t-test doesn't assume equal variances. It calculates standard errors separately for each group and uses a modified degrees of freedom (the Welch-Satterthwaite approximation).

The key insight is that Welch's test is nearly as powerful as the pooled test when variances ARE equal, but much more accurate when they're not. This asymmetry makes Welch's test the recommended default.

Choosing Between Z-Tests and T-Tests

The choice between z-tests and t-tests depends on whether you know the population standard deviation.

The Z-Test: Known Variance

The z-test assumes you know the population standard deviation σ\sigma:

z=xˉ−μ0σ/nz = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}

Under H0H_0, this follows a standard normal distribution N(0,1)N(0, 1).

When do you actually know σ\sigma? Rarely. Possible scenarios include:

  • Measurement instruments with known precision from extensive calibration
  • Standardized tests with established population parameters
  • Very large historical datasets that effectively reveal the population

The T-Test: Unknown Variance

The t-test estimates σ\sigma from the sample using ss:

t=xˉ−μ0s/nt = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}

Under H0H_0, this follows a t-distribution with n−1n-1 degrees of freedom.

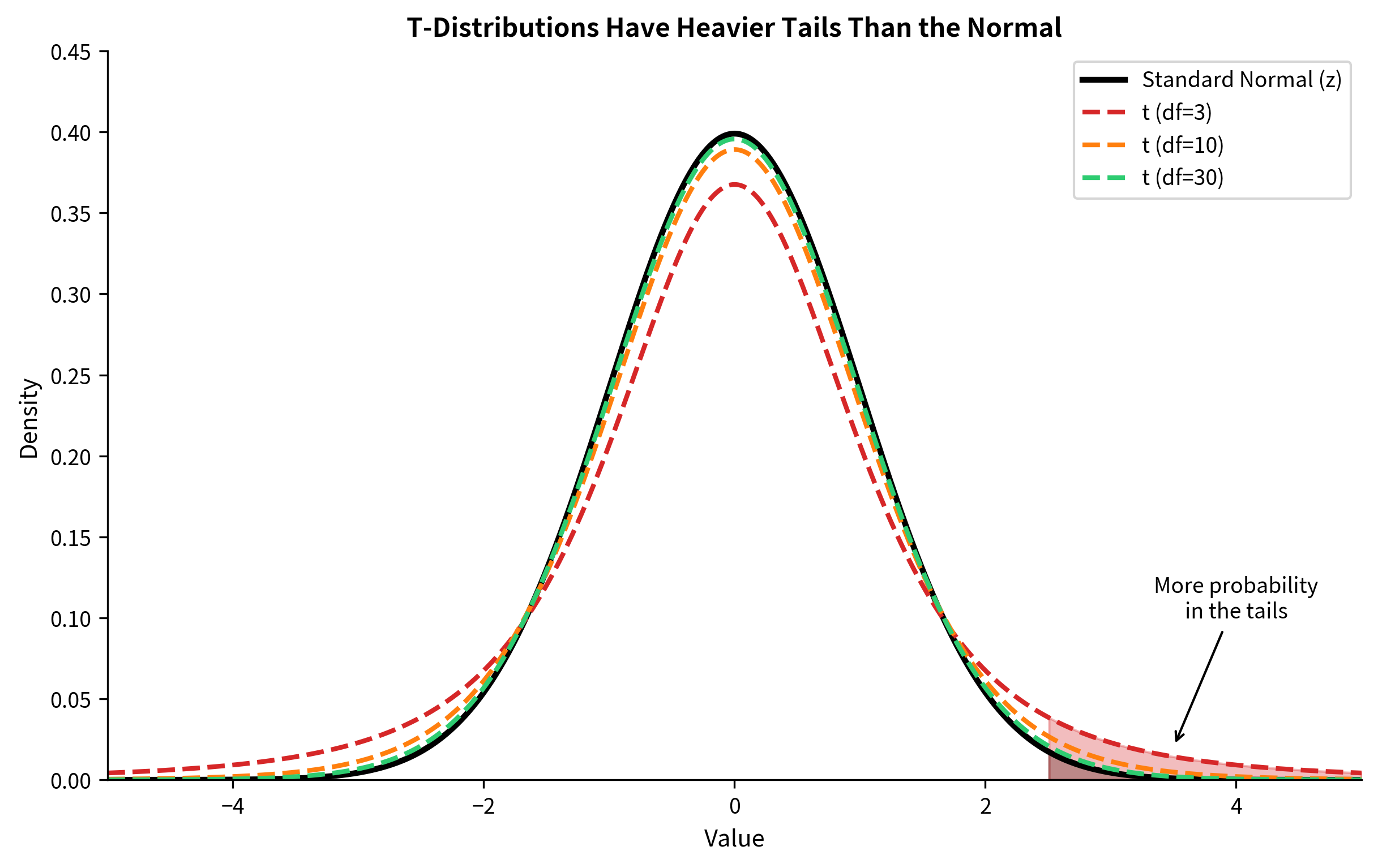
Why the t-distribution? When you estimate σ\sigma with ss, you introduce additional uncertainty. The sample standard deviation ss is itself a random variable. The t-distribution has heavier tails than the normal to account for this uncertainty.

The T-Distribution: Heavy Tails for Small Samples

Out[10]:
Visualization
Line plot comparing t-distributions with different degrees of freedom to the standard normal distribution.
The t-distribution has heavier tails than the normal distribution, especially for small degrees of freedom. This means extreme values are more likely under the t-distribution, which correctly accounts for the uncertainty from estimating σ with s. As df increases, the t-distribution approaches the normal.

The practical consequence: t-tests give larger p-values (and wider confidence intervals) than z-tests for the same data. This is appropriate because we're less certain when we don't know σ\sigma.

Degrees of Freedomt Critical Value (95% CI)Compared to z = 1.96
52.57131% larger
102.22814% larger
202.0866% larger
302.0424% larger
1001.9841% larger
∞1.960Same as z

For practical purposes, with n > 30, the difference between t and z is usually negligible. But always use the t-test when σ\sigma is unknown. There's no benefit to using z when you don't actually know σ\sigma, and it can inflate your Type I error rate for small samples.

Welch's T-Test: The Robust Default

When comparing two independent groups, Welch's t-test should be your default choice.

The Pooled vs Welch Comparison

Pooled (Student's) t-test assumes equal variances:

t=xˉ1−xˉ2sp1n1+1n2wheresp2=(n1−1)s12+(n2−1)s22n1+n2−2t = \frac{\bar{x}_1 - \bar{x}_2}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \quad \text{where} \quad s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}

Welch's t-test allows unequal variances:

t=xˉ1−xˉ2s12n1+s22n2t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}

The degrees of freedom for Welch's test are calculated using the Welch-Satterthwaite formula:

df=(s12n1+s22n2)2(s12/n1)2n1−1+(s22/n2)2n2−1df = \frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2}{\frac{(s_1^2/n_1)^2}{n_1-1} + \frac{(s_2^2/n_2)^2}{n_2-1}}

This formula typically gives a non-integer value for degrees of freedom.

When to Use Which

ConditionRecommended TestReason
Variances clearly equalEither worksPooled slightly more powerful
Variances uncertainWelch'sRobust to violation
Variances clearly unequalWelch'sPooled will be biased
Default choiceWelch'sMinimal cost, high robustness
In[11]:
Code
from scipy import stats
import numpy as np

# Example: Comparing two treatments with different variability
np.random.seed(42)

# Treatment A: Lower mean, lower variance
treatment_a = np.random.normal(50, 5, 25)

# Treatment B: Higher mean, higher variance
treatment_b = np.random.normal(55, 12, 30)

print(
    f"Treatment A: mean = {np.mean(treatment_a):.2f}, std = {np.std(treatment_a, ddof=1):.2f}, n = {len(treatment_a)}"
)
print(
    f"Treatment B: mean = {np.mean(treatment_b):.2f}, std = {np.std(treatment_b, ddof=1):.2f}, n = {len(treatment_b)}"
)
print()

# Pooled t-test (assumes equal variances)
t_pooled, p_pooled = stats.ttest_ind(treatment_a, treatment_b, equal_var=True)
print(f"Pooled t-test:  t = {t_pooled:.3f}, p = {p_pooled:.4f}")

# Welch's t-test (allows unequal variances)
t_welch, p_welch = stats.ttest_ind(treatment_a, treatment_b, equal_var=False)
print(f"Welch's t-test: t = {t_welch:.3f}, p = {p_welch:.4f}")
Out[11]:
Console
Treatment A: mean = 49.18, std = 4.78, n = 25
Treatment B: mean = 52.49, std = 10.79, n = 30

Pooled t-test:  t = -1.418, p = 0.1621
Welch's t-test: t = -1.509, p = 0.1389

In this example, Treatment B has more than twice the variance of Treatment A. The Welch's t-test correctly accounts for this, while the pooled test uses an inappropriate compromise variance estimate.

Summary

This chapter covered two essential complementary topics:

Confidence Intervals and Their Equivalence to Hypothesis Tests

  • A 95% CI contains all parameter values that would not be rejected at the 0.05 level
  • CIs are more informative than p-values because they show the range of plausible values
  • CI width communicates precision: narrow intervals indicate precise estimates

Test Assumptions

  • Independence: The most important assumption. Violations lead to inflated Type I errors.
  • Normality: The CLT makes this less critical for large samples (n > 30), but small samples require caution
  • Equal variances: Use Welch's t-test as your default for two-sample comparisons

Choosing Between Tests

  • Use t-tests when σ\sigma is unknown (almost always)
  • Use Welch's t-test as the default for two-sample comparisons
  • The z-test is appropriate only when you genuinely know σ\sigma from prior information

What's Next

In the next chapter, The Z-Test, we'll explore z-tests in depth: one-sample tests, two-sample tests, and tests for proportions. You'll learn when the z-test is appropriate and how to apply it correctly.

Subsequent chapters cover the t-test (the workhorse of hypothesis testing), the F-test for comparing variances, ANOVA for comparing multiple groups, Type I and Type II errors, power analysis, effect sizes, and multiple comparison corrections. Each chapter builds on the foundations established here.

Quiz

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about confidence intervals and test assumptions.

Loading component...

Reference

BIBTEXAcademic
@misc{confidenceintervalsandtestassumptions, author = {Michael Brenndoerfer}, title = {Confidence Intervals and Test Assumptions}, year = {2026}, url = {https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-01-01} }
APAAcademic
Michael Brenndoerfer (2026). Confidence Intervals and Test Assumptions. Retrieved from https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing
MLAAcademic
Michael Brenndoerfer. "Confidence Intervals and Test Assumptions." 2026. Web. today. <https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing>.
CHICAGOAcademic
Michael Brenndoerfer. "Confidence Intervals and Test Assumptions." Accessed today. https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing.
HARVARDAcademic
Michael Brenndoerfer (2026) 'Confidence Intervals and Test Assumptions'. Available at: https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing (Accessed: today).
SimpleBasic
Michael Brenndoerfer (2026). Confidence Intervals and Test Assumptions. https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing
Direct link:
https://mbrenndoerfer.com/writing/confidence-intervals-test-assumptions-z-test-t-test-choosing