WritingBooksAboutCommunityContactCommunity

ML Trading Strategies: Signal Generation, Sentiment & RL

Michael Brenndoerfer•January 3, 2026•64 min read

Build ML-driven trading strategies covering return prediction, sentiment analysis, alternative data integration, and reinforcement learning for execution.

Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Machine Learning in Trading Strategy Design

The previous chapter introduced the core machine learning techniques used in trading: supervised learning and unsupervised learning algorithms, feature engineering approaches, and the critical importance of avoiding lookahead bias. Now we turn to how these techniques integrate into complete trading strategy design workflows. This chapter bridges the gap between ML algorithms and actionable trading signals, covering the end-to-end process of building ML-driven strategies.

Modern quantitative trading has moved far beyond simple factor models and technical indicators. Machine learning enables strategies that can adapt to changing market conditions, extract signals from unstructured data like news articles and satellite imagery, and optimize execution in ways that would be impossible with traditional methods. However, this power comes with significant challenges: the risk of overfitting to noise, the difficulty of explaining model decisions to risk managers and regulators, and the computational infrastructure required to deploy these systems at scale.

We'll explore four major applications: using ML for return prediction and signal generation, extracting sentiment from text data, incorporating alternative data sources, and applying reinforcement learning to dynamic trading decisions. Throughout, we'll emphasize the practical considerations that determine whether an ML strategy succeeds in live markets or fails when it encounters conditions not represented in its training data.

ML for Signal Generation

Signal generation is the process of transforming raw market data and features into predictions that drive trading decisions. Building on the feature engineering concepts from the previous chapter, we now focus on constructing complete prediction pipelines that generate tradable signals.

Return Prediction with Supervised Learning

The most direct application of supervised learning in trading is predicting future returns. To understand why this problem is so challenging, consider what we're attempting: given a feature vector xt\mathbf{x}_t observed at time tt, we want to predict the return rt+hr_{t+h} over some horizon hh. This seemingly simple objective masks profound complexity, because financial returns are among the most difficult quantities to predict in any domain. Markets aggregate information from millions of participants, each acting on their own analysis, making prices highly efficient and prediction exceptionally difficult.

This prediction task can be framed as either regression (predicting the magnitude of returns) or classification (predicting whether returns will be positive or negative). The choice between these two approaches involves substantive tradeoffs that affect strategy design. Regression provides continuous predictions that can be used for position sizing, allowing you to bet more heavily when the model predicts larger returns. However, return distributions are notoriously noisy and heavy-tailed, making accurate point predictions extraordinarily difficult. The distribution of daily returns has fat tails and exhibits volatility clustering, meaning that the assumption of normal, well-behaved errors underlying many regression models is violated.

Classification simplifies the problem to directional prediction, asking only whether the next return will be positive or negative. This binary framing discards information about magnitude but may be more robust to the noise inherent in return data. In practice, many strategies use classification with probability outputs, where the predicted probability serves as a signal strength measure. A model that predicts a 70% probability of positive returns conveys more conviction than one predicting 52%, even though both would be classified as "positive." This probability can then inform position sizing decisions.

Let's build a complete signal generation pipeline for equity returns:

In[2]:
Code
import numpy as np
import pandas as pd
import warnings

warnings.filterwarnings("ignore")

np.random.seed(42)

# Generate synthetic price data for demonstration
n_days = 2000
dates = pd.date_range("2018-01-01", periods=n_days, freq="B")

# Create correlated asset returns with some predictable structure
market_returns = np.random.normal(0.0003, 0.012, n_days)
idiosyncratic = np.random.normal(0, 0.015, n_days)
momentum_signal = np.zeros(n_days)

# Add momentum effect: past returns predict future returns
for i in range(21, n_days):
    momentum_signal[i] = np.mean(market_returns[i - 21 : i]) * 0.3

stock_returns = (
    0.8 * market_returns
    + idiosyncratic
    + momentum_signal
    + np.random.normal(0, 0.008, n_days)
)
prices = 100 * np.exp(np.cumsum(stock_returns))

df = pd.DataFrame(
    {
        "date": dates,
        "price": prices,
        "return": stock_returns,
        "market_return": market_returns,
    }
).set_index("date")
In[3]:
Code
def create_features(df, lookback_windows=[5, 10, 21, 63]):
    """
    Create technical features for return prediction.
    Uses only past information to avoid lookahead bias.
    """
    features = pd.DataFrame(index=df.index)

    # Momentum features: past returns over various windows
    for window in lookback_windows:
        features[f"momentum_{window}d"] = df["return"].rolling(window).sum()
        features[f"volatility_{window}d"] = df["return"].rolling(window).std()

    # Mean reversion signal: deviation from moving average
    for window in [21, 63]:
        ma = df["price"].rolling(window).mean()
        features[f"ma_deviation_{window}d"] = (df["price"] - ma) / ma

    # Volume-weighted features (simulated volume)
    df["volume"] = np.random.lognormal(10, 0.5, len(df)) * (
        1 + df["return"].abs()
    )
    features["volume_ratio"] = df["volume"] / df["volume"].rolling(21).mean()

    # Higher moments: skewness and kurtosis of recent returns
    features["skewness_21d"] = df["return"].rolling(21).skew()
    features["kurtosis_21d"] = df["return"].rolling(21).kurt()

    # Market beta (rolling regression coefficient)
    def rolling_beta(returns, market_returns, window):
        cov = returns.rolling(window).cov(market_returns)
        var = market_returns.rolling(window).var()
        return cov / var

    features["beta_63d"] = rolling_beta(df["return"], df["market_return"], 63)

    return features


features = create_features(df)

The feature set combines momentum indicators, volatility measures, mean-reversion signals, and market sensitivity metrics. Each of these feature categories captures a different aspect of market behavior that academic research and practitioner experience have identified as potentially predictive. Momentum features exploit the tendency for past winners to continue outperforming in the short term. Volatility features capture the risk environment, since returns may behave differently during calm versus turbulent periods. Mean-reversion signals detect when prices have strayed from their recent average, potentially setting up for a reversal. Market beta measures each asset's sensitivity to broad market movements, which can inform both directional predictions and risk management. Critically, each feature uses only information available at time tt to predict returns at t+1t+1, ensuring no lookahead bias contaminates the model.

In[4]:
Code
from sklearn.preprocessing import StandardScaler

# Create target variable: next-day return direction
df["target"] = (df["return"].shift(-1) > 0).astype(int)

# Combine features and target, dropping rows with NaN values
data = features.join(df[["target", "return"]]).dropna()

# Split into training and test sets using temporal ordering
# Use first 70% for training, last 30% for testing
split_idx = int(len(data) * 0.7)
train_data = data.iloc[:split_idx]
test_data = data.iloc[split_idx:]

feature_cols = features.columns.tolist()
X_train = train_data[feature_cols]
y_train = train_data["target"]
X_test = test_data[feature_cols]
y_test = test_data["target"]

# Scale features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
In[5]:
Code
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, precision_score, roc_auc_score

# Train multiple models for comparison
models = {
    "Logistic Regression": LogisticRegression(C=0.1, max_iter=1000),
    "Random Forest": RandomForestClassifier(
        n_estimators=100, max_depth=5, min_samples_leaf=20
    ),
    "Gradient Boosting": GradientBoostingClassifier(
        n_estimators=100, max_depth=3, learning_rate=0.05
    ),
}

results = {}
predictions = {}

for name, model in models.items():
    model.fit(X_train_scaled, y_train)

    # Get probability predictions for the positive class
    y_pred_proba = model.predict_proba(X_test_scaled)[:, 1]
    y_pred = (y_pred_proba > 0.5).astype(int)

    results[name] = {
        "accuracy": accuracy_score(y_test, y_pred),
        "precision": precision_score(y_test, y_pred),
        "auc": roc_auc_score(y_test, y_pred_proba),
    }
    predictions[name] = y_pred_proba
Out[6]:
Console
Model Performance Comparison (Out-of-Sample)
=======================================================

Logistic Regression:
  Accuracy:  0.495
  Precision: 0.499
  AUC-ROC:   0.494

Random Forest:
  Accuracy:  0.510
  Precision: 0.511
  AUC-ROC:   0.502

Gradient Boosting:
  Accuracy:  0.500
  Precision: 0.503
  AUC-ROC:   0.500
Out[7]:
Visualization
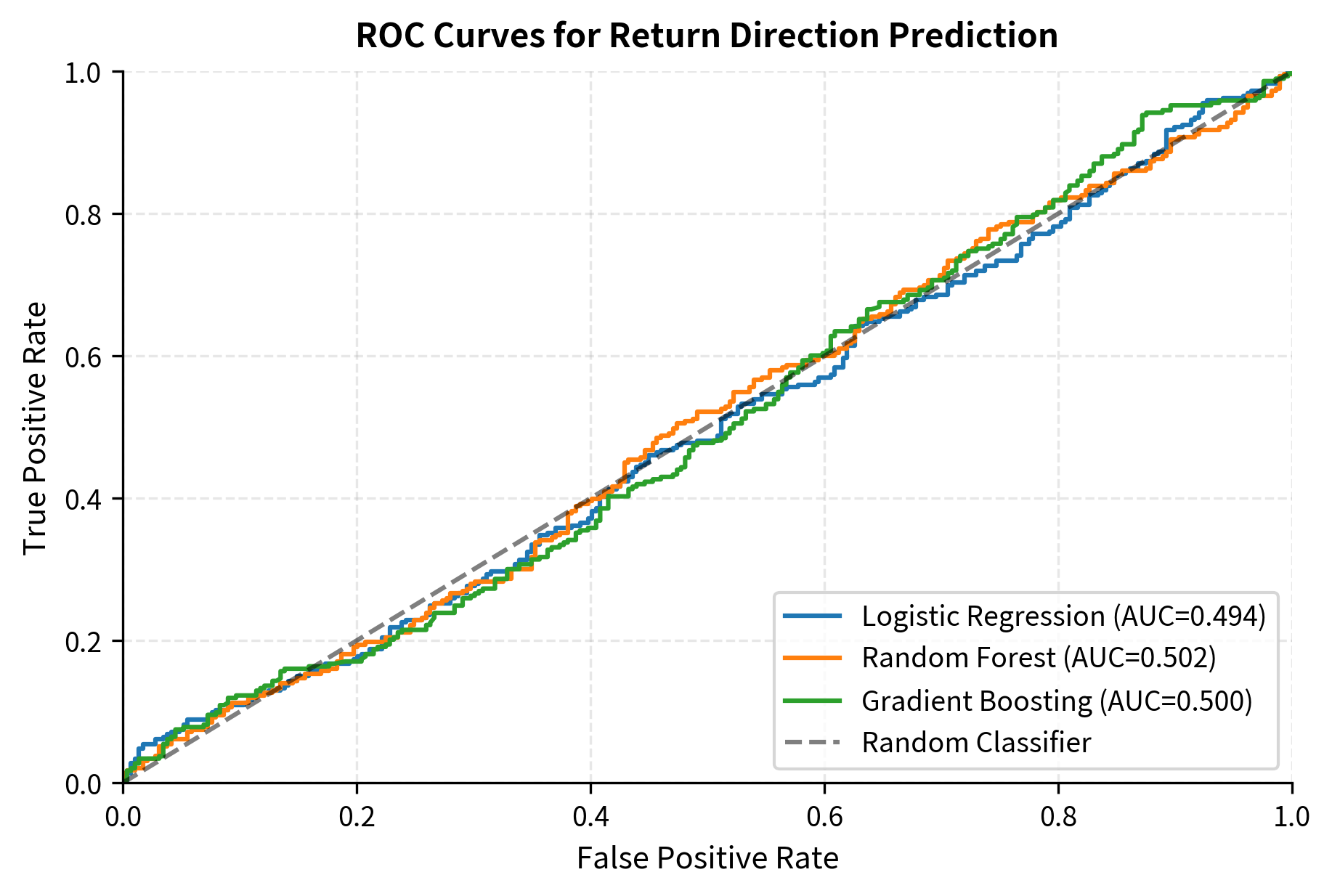
ROC curves for three classification models (Logistic Regression, Random Forest, Gradient Boosting). All models show modest predictive power with AUC values slightly above 0.5, illustrating the difficulty of forecasting directional equity returns.
ROC curves for three classification models (Logistic Regression, Random Forest, Gradient Boosting). All models show modest predictive power with AUC values slightly above 0.5, illustrating the difficulty of forecasting directional equity returns.

The results reveal a crucial reality of return prediction: accuracy barely exceeds 50%. This isn't a failure of the models or an indication that better algorithms would solve the problem. Instead, it reflects the fundamental difficulty of predicting financial returns. Markets are highly competitive, and any easily exploitable signal gets arbitraged away as sophisticated traders discover and trade on it. The efficient market hypothesis, while not perfectly descriptive, captures an important truth: prices incorporate information quickly, leaving little room for systematic prediction.

The AUC scores slightly above 0.5 indicate that the models capture some genuine predictive information, but the signal-to-noise ratio is extremely low. To put this in perspective, an AUC of 0.52 means that if you randomly select a positive case (day with positive returns) and a negative case, the model ranks the positive case higher only 52% of the time. This slim edge might seem negligible, but when applied consistently across many assets and time periods, even small advantages compound into meaningful returns. The challenge lies in extracting this weak signal reliably without overfitting to noise.

Converting Predictions to Trading Signals

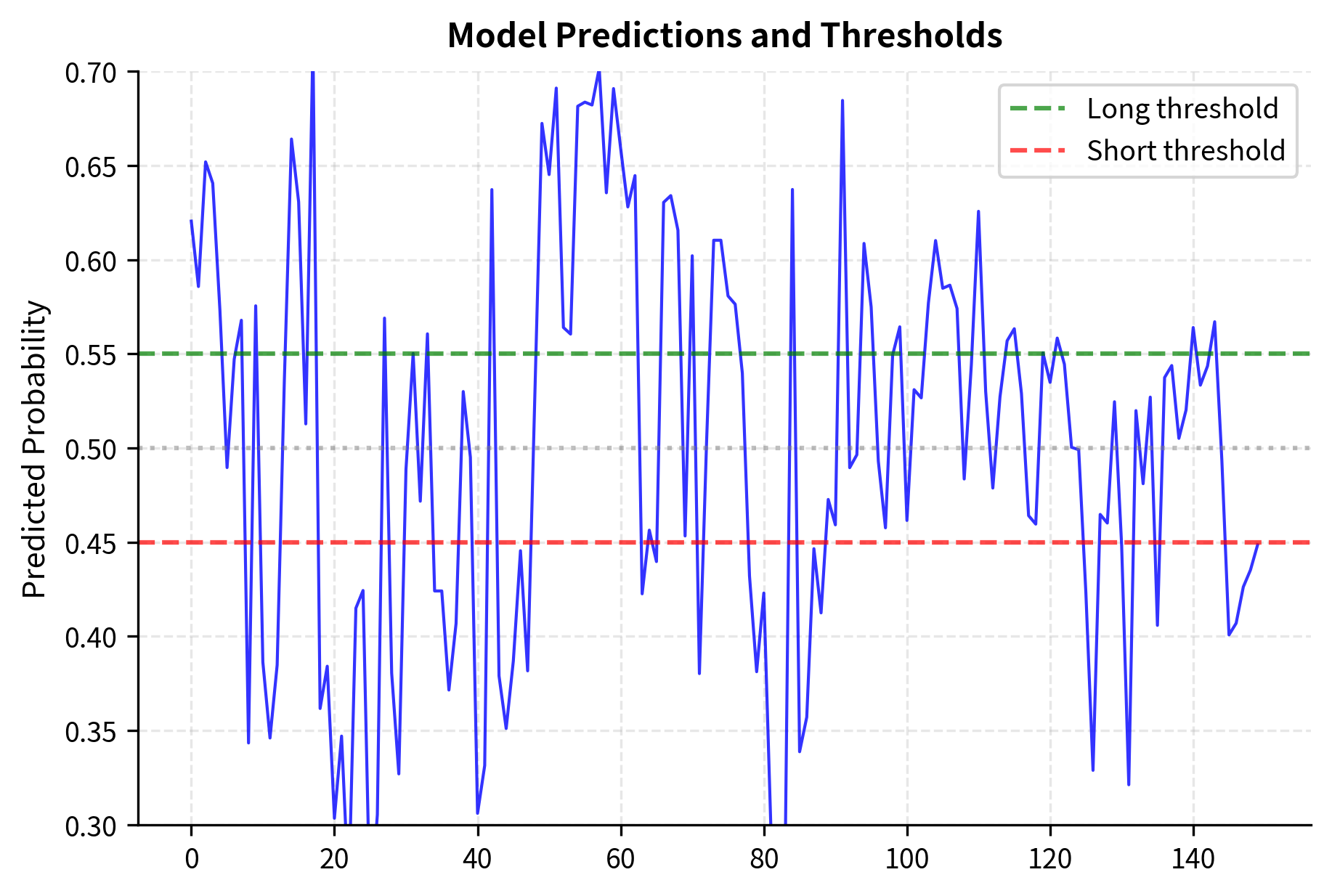
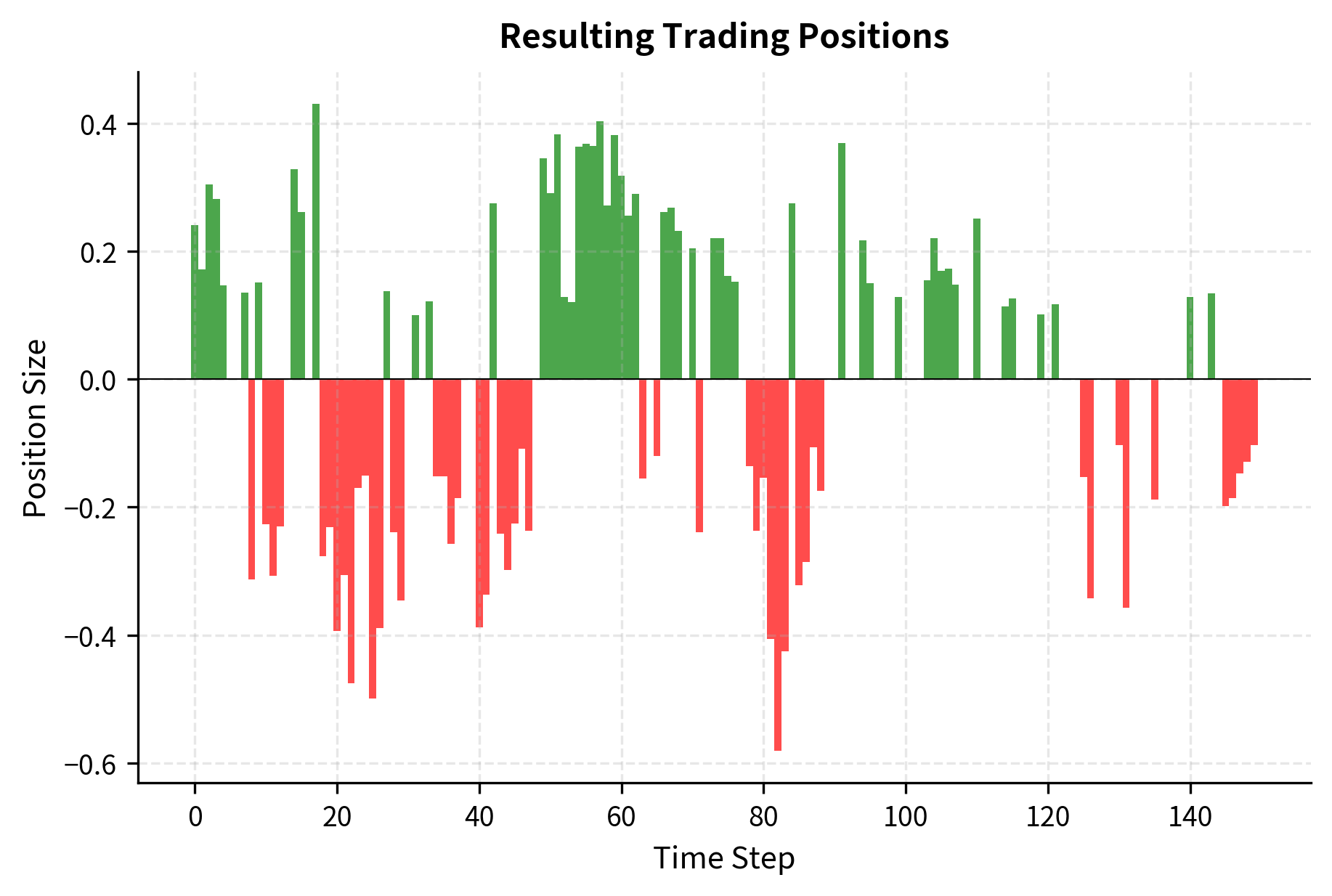
Raw model predictions must be transformed into actionable trading signals before they can generate trades. This transformation step involves deciding not only the direction of trades but also their size and the conditions under which to trade at all. A common approach uses predicted probabilities to determine both direction and position size:

In[8]:
Code
def predictions_to_signals(
    probabilities, threshold_long=0.55, threshold_short=0.45
):
    """
    Convert probability predictions to trading signals.

    Parameters:

    - probabilities: Predicted probability of positive return
    - threshold_long: Probability above which to go long
    - threshold_short: Probability below which to go short

    Returns:

    - signals: -1 (short), 0 (no position), +1 (long)
    - position_sizes: Scaled by confidence (distance from 0.5)
    """
    signals = np.zeros(len(probabilities))
    signals[probabilities > threshold_long] = 1
    signals[probabilities < threshold_short] = -1

    # Scale position size by confidence
    # Maximum confidence at probability 0 or 1, minimum at 0.5
    confidence = np.abs(probabilities - 0.5) * 2
    position_sizes = signals * confidence

    return signals, position_sizes


# Apply to gradient boosting predictions
signals, position_sizes = predictions_to_signals(
    predictions["Gradient Boosting"]
)
Out[9]:
Console
Signal Distribution:
  Long signals:  221 (38.0%)
  Short signals: 163 (28.0%)
  No position:   198 (34.0%)

Average position size when active: 0.239
Out[10]:
Visualization
Predicted probability of positive returns over time relative to trading thresholds. The green (0.55) and red (0.45) dashed lines define high-conviction zones, allowing the strategy to filter out low-confidence signals near the 0.5 neutral level and trade only when the model indicates a strong directional edge.
Predicted probability of positive returns over time relative to trading thresholds. The green (0.55) and red (0.45) dashed lines define high-conviction zones, allowing the strategy to filter out low-confidence signals near the 0.5 neutral level and trade only when the model indicates a strong directional edge.
Out[11]:
Visualization
Trading position sizes dynamically scaled by model confidence. Green bars represent long positions and red bars represent short positions, with magnitudes proportional to the distance of the predicted probability from 0.5. This sizing mechanism allocates more capital to high-conviction signals while reducing exposure during uncertain periods.
Trading position sizes dynamically scaled by model confidence. Green bars represent long positions and red bars represent short positions, with magnitudes proportional to the distance of the predicted probability from 0.5. This sizing mechanism allocates more capital to high-conviction signals while reducing exposure during uncertain periods.

The threshold approach embodies an important principle: not every prediction deserves a trade. By filtering out low-conviction predictions (those close to 50% probability), the strategy only takes positions when the model has sufficient confidence. This filtering serves multiple purposes. It reduces turnover and the associated transaction costs, which can erode returns quickly in frequent-trading strategies. It focuses capital on the highest-quality signals where the model's edge is most pronounced. And it acknowledges the reality that predictions near the decision boundary are essentially random guesses dressed up with spurious precision.

The position sizing component extends this logic further. Rather than taking equal-sized positions regardless of conviction, the strategy scales position size by the model's confidence, measured as the distance from 50%. A prediction of 70% positive return leads to a larger position than a prediction of 56%, reflecting the intuition that stronger signals warrant more capital allocation. This confidence-weighted sizing can significantly improve risk-adjusted returns by ensuring that the portfolio's exposure concentrates in the model's highest-conviction bets.

Evaluating Signal Quality

Beyond classification metrics like accuracy and AUC, we need to evaluate how signals translate into actual trading performance. The connection between prediction quality and trading profit is not straightforward. A model might achieve 55% accuracy, but if its correct predictions tend to coincide with small moves while incorrect predictions coincide with large moves, the trading results could be disappointing.

The information coefficient (IC), which we discussed in Part IV, measures the correlation between predicted and realized returns. This metric directly captures whether the model's signal strength corresponds to return magnitude:

In[12]:
Code
def evaluate_signals(signals, actual_returns):
    """
    Evaluate trading signal quality with multiple metrics.
    """
    # Information Coefficient: correlation between signal and actual return
    ic = np.corrcoef(signals, actual_returns)[0, 1]

    # Hit rate: percentage of correct directional predictions
    # Only count positions where we had a signal
    active_mask = signals != 0
    if active_mask.sum() > 0:
        correct_direction = np.sign(signals[active_mask]) == np.sign(
            actual_returns[active_mask]
        )
        hit_rate = correct_direction.mean()
    else:
        hit_rate = np.nan

    # Profit factor: gross profits / gross losses
    returns_from_signal = signals * actual_returns
    gross_profit = returns_from_signal[returns_from_signal > 0].sum()
    gross_loss = -returns_from_signal[returns_from_signal < 0].sum()
    profit_factor = gross_profit / gross_loss if gross_loss > 0 else np.inf

    return {
        "information_coefficient": ic,
        "hit_rate": hit_rate,
        "profit_factor": profit_factor,
    }


# Evaluate signals against actual next-day returns
actual_returns = test_data["return"].shift(-1).iloc[:-1].values
eval_signals = signals[:-1]  # Align with returns

signal_quality = evaluate_signals(eval_signals, actual_returns)
Out[13]:
Console
Signal Quality Metrics:
  Information Coefficient: -0.0478
  Hit Rate:                49.1%
  Profit Factor:           0.87

The information coefficient is small but positive, indicating weak but genuine predictive power. Understanding what these numbers mean in context is essential. In the world of trading, even an IC of 0.02 to 0.05 can be valuable when applied across many assets and combined with appropriate leverage. Consider a strategy trading 500 stocks daily: with an IC of 0.03, the model provides a small but consistent edge on each trade that, when aggregated across the entire portfolio, can generate attractive returns.

The profit factor above 1.0 provides complementary information. It tells us that the strategy generates more profit on winning trades than it loses on losing trades. A profit factor of 1.2, for instance, means that for every dollar lost on losing trades, the strategy earns \$1.20 on winning trades. Combined with the hit rate, these metrics paint a complete picture of strategy economics: how often we win, how much we win when we're right, and how much we lose when we're wrong.

Regime-Aware Signal Generation

Market conditions change over time, and a model trained on one regime may fail spectacularly in another. During a strong bull market, momentum strategies thrive as trends persist. During volatile sideways markets, mean-reversion strategies often perform better. A model that doesn't account for these regime shifts will apply momentum signals during ranging markets and mean-reversion signals during trends, suffering losses in both cases.

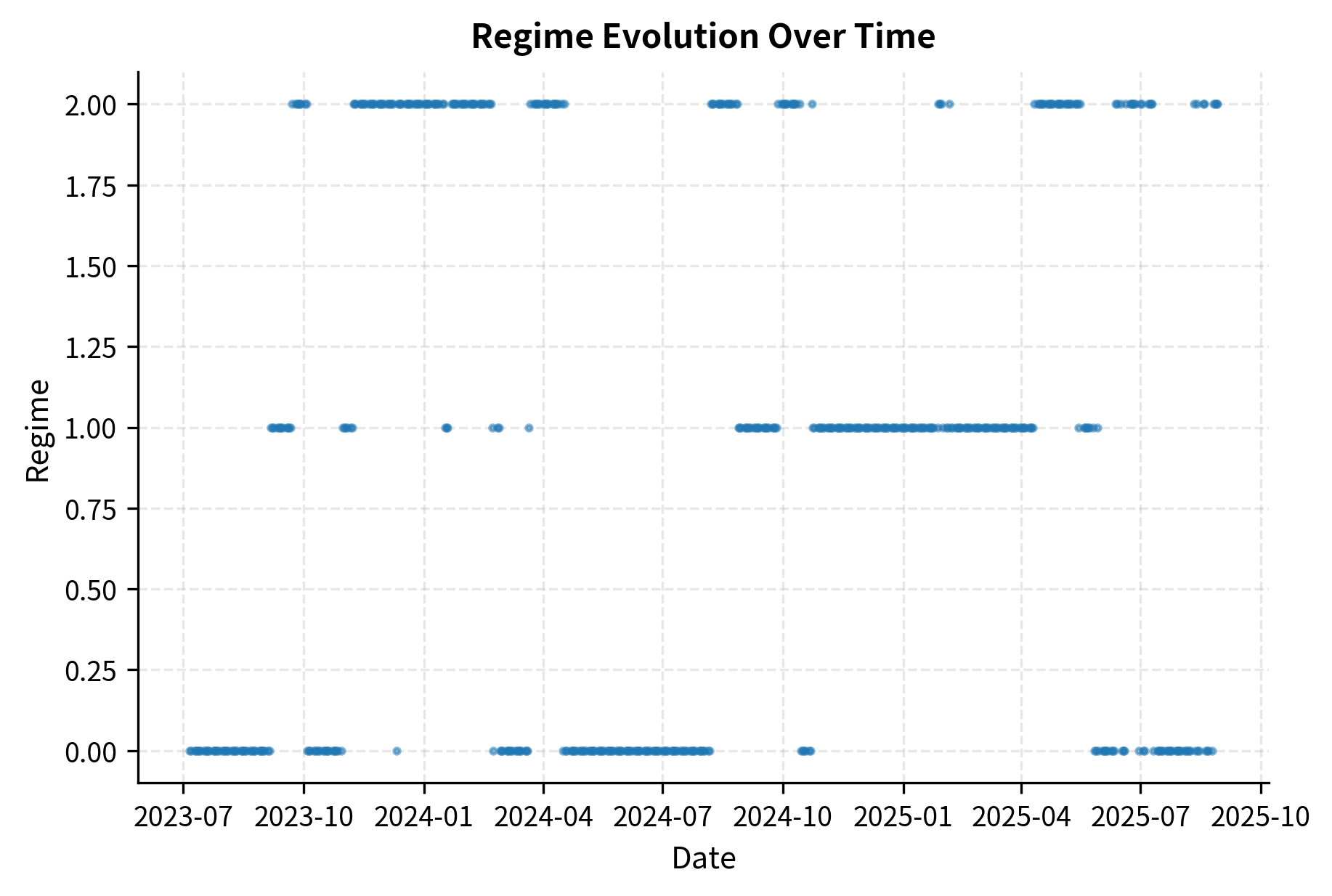
Regime-aware approaches address this challenge by first identifying the current market state, then adjusting predictions based on the detected regime:

In[14]:
Code
from sklearn.mixture import GaussianMixture


def detect_regime(returns, volatility, n_regimes=3):
    """
    Detect market regime using Gaussian Mixture Model on returns and volatility.
    """
    # Prepare features for regime detection
    regime_features = np.column_stack(
        [returns.rolling(21).mean().values, volatility.values]
    )

    # Remove NaN values
    valid_mask = ~np.isnan(regime_features).any(axis=1)

    # Fit GMM
    gmm = GaussianMixture(
        n_components=n_regimes, random_state=42, covariance_type="full"
    )
    regimes = np.full(len(returns), np.nan)
    regimes[valid_mask] = gmm.fit_predict(regime_features[valid_mask])

    return regimes, gmm


# Detect regimes in test data
test_volatility = test_data["volatility_21d"]
test_returns_series = test_data["return"]
regimes, gmm = detect_regime(test_returns_series, test_volatility)
In[15]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Visualize regimes - Plot 1: Scatter
plt.figure()
valid_idx = ~np.isnan(regimes)
scatter = plt.scatter(
    test_data.loc[valid_idx, "momentum_21d"],
    test_data.loc[valid_idx, "volatility_21d"],
    c=regimes[valid_idx],
    cmap="viridis",
    alpha=0.5,
    s=20,
)
plt.xlabel("21-Day Momentum")
plt.ylabel("21-Day Volatility")
plt.title("Market Regime Detection")
plt.legend(*scatter.legend_elements(), title="Regime")
plt.show()
Out[15]:
Visualization
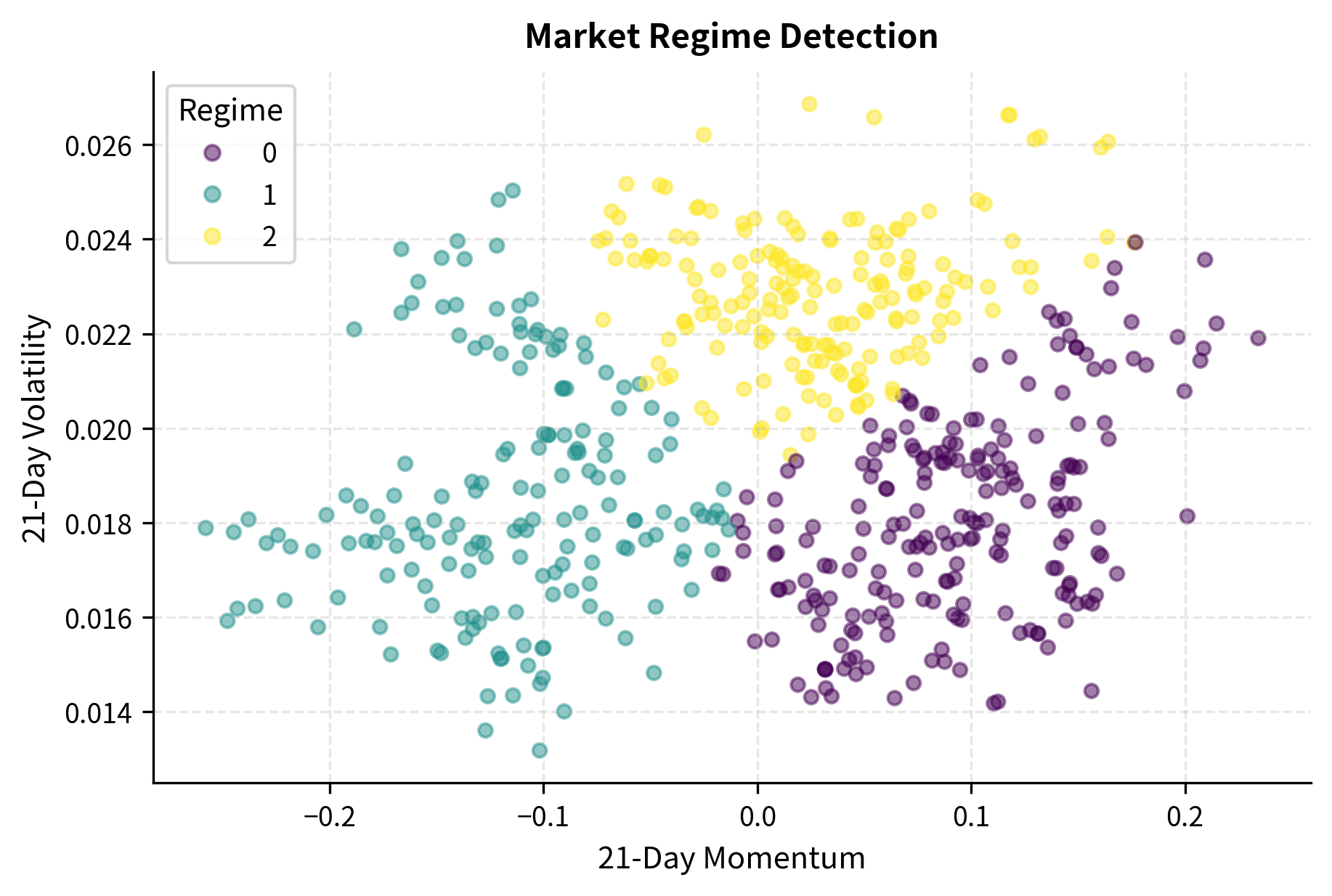
Scatter plot of market regimes with returns on x-axis and volatility on y-axis, colored by regime.
Market regime classification using a Gaussian Mixture Model based on 21-day momentum and volatility. The scatter plot reveals distinct clusters corresponding to trending states (low volatility), stressed markets (high volatility), and transitional periods. These detected regimes allow the strategy to adapt its signal generation logic to prevailing market conditions.
In[16]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Visualize regimes - Plot 2: Time Series
plt.figure()
# Re-calculate valid_idx to ensure independence
valid_idx = ~np.isnan(regimes)
plt.plot(
    test_data.index[valid_idx], regimes[valid_idx], "o", markersize=2, alpha=0.5
)
plt.xlabel("Date")
plt.ylabel("Regime")
plt.title("Regime Evolution Over Time")
plt.show()
Out[16]:
Visualization
Time series evolution of detected market regimes over the test period. The distinct bands show how the market transitions between stable, trending, and volatile states, enabling the strategy to dynamically switch between momentum and mean-reversion logic based on the active regime.
Time series evolution of detected market regimes over the test period. The distinct bands show how the market transitions between stable, trending, and volatile states, enabling the strategy to dynamically switch between momentum and mean-reversion logic based on the active regime.

Regime detection enables strategies to adapt their behavior to current market conditions. In practice, you might use momentum signals more aggressively in trending regimes, where past returns have historically predicted future returns, while switching to mean-reversion signals in ranging regimes, where prices oscillate around stable levels. The regime model serves as a meta-layer that conditions the primary prediction model, effectively learning "when" different patterns apply rather than just "what" patterns exist.

The Gaussian Mixture Model approach shown here identifies regimes based on the joint distribution of recent returns and volatility. The three identified regimes typically correspond to distinct market states: calm trending periods with low volatility and consistent directional movement, high-volatility periods often associated with market stress or major uncertainty, and transitional periods that don't fit neatly into either category. By recognizing which regime the market currently occupies, the strategy can apply the most appropriate trading rules for that environment. The next chapter on alternative data explores how external information can improve regime identification beyond what price data alone reveals.

Key Parameters

The key parameters for the supervised learning and regime detection models are:

  • n_estimators: The number of trees in the Random Forest or Gradient Boosting model. More trees generally improve stability but increase training time.
  • max_depth: The maximum depth of each tree. Constraining depth helps prevent overfitting to noise in financial data.
  • learning_rate: Determines the contribution of each tree in Gradient Boosting. Lower rates with more trees often yield better generalization.
  • n_components: The number of regimes (clusters) in the Gaussian Mixture Model. This defines how many distinct market states the model attempts to identify.

Sentiment Analysis for Trading Signals

Financial markets are driven not just by fundamentals but by collective psychology. The beliefs, fears, and expectations of market participants manifest in price movements, but they also leave traces in the vast corpus of financial text produced daily. News articles, earnings call transcripts, social media posts, and analyst reports contain information about market sentiment that can predict price movements. Natural language processing (NLP) techniques transform this unstructured text data into quantitative trading signals.

The intuition behind sentiment analysis for trading is straightforward: if we can systematically measure whether market commentary is becoming more optimistic or pessimistic, we might anticipate the buying or selling pressure that follows. When analysts upgrade their tone, when news coverage shifts from concerns to opportunities, when executives speak more confidently on earnings calls, these verbal signals often precede tangible market moves. The challenge lies in converting messy human language into clean numerical signals that trading algorithms can consume.

Text Preprocessing for Financial Data

Financial text requires domain-specific preprocessing. Standard NLP techniques must be adapted to handle ticker symbols, numerical expressions, financial jargon, and the particular ways sentiment is expressed in market contexts. A preprocessing pipeline that works well for movie reviews will struggle with the peculiarities of financial language.

Consider the differences: financial text contains dense numerical information (revenue figures, growth percentages, price targets) that carries meaning. It uses abbreviations and acronyms specific to the industry (EPS, EBITDA, YoY). Ticker symbols appear frequently and must be recognized and associated with their respective companies. Temporal references are crucial, since a statement about "last quarter" means something very different from one about "next fiscal year." These domain-specific features require careful handling:

In[17]:
Code
import re


def preprocess_financial_text(text):
    """
    Preprocess financial text for sentiment analysis.
    """
    # Convert to lowercase
    text = text.lower()

    # Preserve ticker symbols (typically $AAPL or just AAPL)
    ticker_pattern = r"\$?[A-Z]{1,5}(?=\s|$|,|\.)"
    tickers = re.findall(ticker_pattern, text, re.IGNORECASE)

    # Handle common financial abbreviations
    abbreviations = {
        "q1": "first quarter",
        "q2": "second quarter",
        "q3": "third quarter",
        "q4": "fourth quarter",
        "yoy": "year over year",
        "qoq": "quarter over quarter",
        "eps": "earnings per share",
        "p/e": "price to earnings",
        "roi": "return on investment",
        "ebitda": "ebitda",
    }
    for abbr, expansion in abbreviations.items():
        text = re.sub(r"\b" + abbr + r"\b", expansion, text)

    # Remove URLs
    text = re.sub(r"http\S+|www\.\S+", "", text)

    # Remove special characters but keep sentence structure
    text = re.sub(r"[^\w\s\.\,\!\?]", "", text)

    # Normalize whitespace
    text = " ".join(text.split())

    return text, tickers


# Example financial headlines
headlines = [
    "Apple beats Q3 earnings estimates, stock surges 5% in after-hours trading",
    "Fed signals rate cuts ahead, markets rally on dovish commentary",
    "Tesla misses delivery targets, shares plunge amid production concerns",
    "Goldman Sachs upgrades MSFT to buy, cites cloud growth momentum",
    "Oil prices crash as OPEC+ fails to reach production agreement",
]

processed_headlines = [preprocess_financial_text(h) for h in headlines]
Out[18]:
Console
Preprocessed Headlines:
------------------------------------------------------------
Original: Apple beats Q3 earnings estimates, stock surges 5%...
Processed: apple beats third quarter earnings estimates, stoc...
Tickers: ['apple', 'beats', 'nings', 'mates', 'stock', 'urges', 'in', 'hours', 'ading']

Original: Fed signals rate cuts ahead, markets rally on dovi...
Processed: fed signals rate cuts ahead, markets rally on dovi...
Tickers: ['fed', 'gnals', 'rate', 'cuts', 'ahead', 'rkets', 'rally', 'on', 'ovish', 'ntary']

Original: Tesla misses delivery targets, shares plunge amid ...
Processed: tesla misses delivery targets, shares plunge amid ...
Tickers: ['tesla', 'isses', 'ivery', 'rgets', 'hares', 'lunge', 'amid', 'ction', 'cerns']

Original: Goldman Sachs upgrades MSFT to buy, cites cloud gr...
Processed: goldman sachs upgrades msft to buy, cites cloud gr...
Tickers: ['ldman', 'sachs', 'rades', 'msft', 'to', 'buy', 'cites', 'cloud', 'rowth', 'entum']

Original: Oil prices crash as OPEC+ fails to reach productio...
Processed: oil prices crash as opec fails to reach production...
Tickers: ['oil', 'rices', 'crash', 'as', 'fails', 'to', 'reach', 'ction', 'ement']

Preprocessing standardizes the text structure, separating ticker symbols for entity linking and expanding abbreviations to improve consistency across sources. This normalization ensures that the sentiment model focuses on meaningful content rather than formatting variations. Without this step, the same underlying sentiment could appear in many different surface forms, making it harder for the model to learn robust patterns.

Dictionary-Based Sentiment Analysis

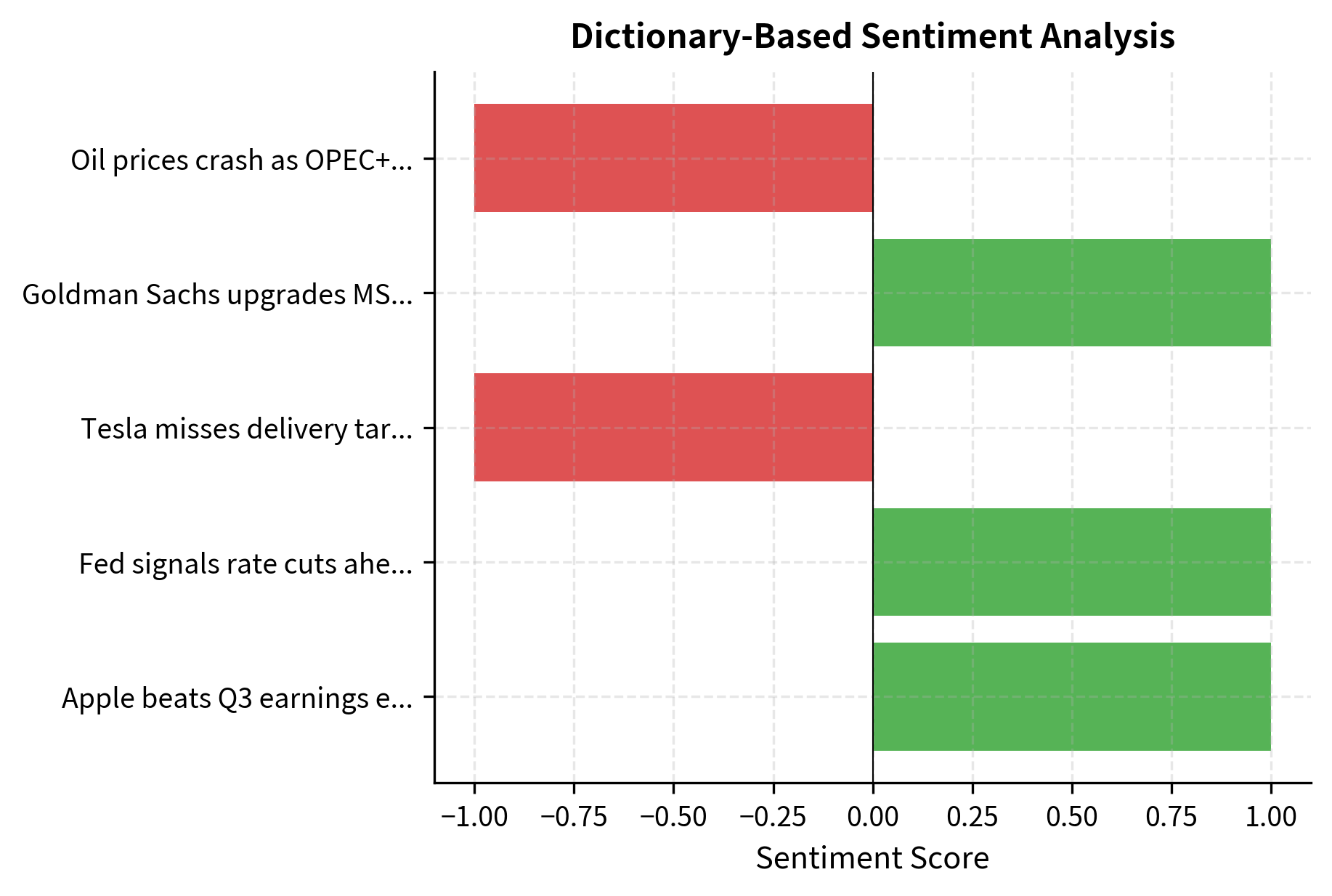
The simplest approach to sentiment analysis uses predefined dictionaries of positive and negative words. When encountering text, the algorithm counts occurrences of words from each category and computes a sentiment score based on the balance. Financial-specific dictionaries like Loughran-McDonald are particularly effective because they account for how words carry different connotations in financial versus general contexts.

This domain specificity is crucial. Consider the word "liability": in everyday speech, it's neutral or only mildly negative ("he's a liability to the team"), but in financial contexts, it refers to debts and obligations, carrying a more clearly negative connotation. Similarly, "tax" might be neutral in general text but signals a drag on earnings in financial analysis. Words like "leverage" and "risk" require careful handling, as they can be positive or negative depending on context. General-purpose sentiment dictionaries, trained on movie reviews or product feedback, will misclassify these terms and produce unreliable signals.

In[19]:
Code
# Financial sentiment lexicon (simplified Loughran-McDonald style)
positive_words = {
    "beat",
    "beats",
    "exceeded",
    "surged",
    "surge",
    "rally",
    "rallied",
    "upgrade",
    "upgrades",
    "growth",
    "profit",
    "profitable",
    "gain",
    "gains",
    "positive",
    "strong",
    "strength",
    "outperform",
    "buy",
    "bullish",
    "momentum",
    "opportunity",
    "success",
    "successful",
    "improve",
    "improved",
}

negative_words = {
    "miss",
    "misses",
    "missed",
    "plunge",
    "plunged",
    "crash",
    "crashed",
    "downgrade",
    "downgrades",
    "loss",
    "losses",
    "decline",
    "declined",
    "negative",
    "weak",
    "weakness",
    "underperform",
    "sell",
    "bearish",
    "concern",
    "concerns",
    "risk",
    "risks",
    "fail",
    "failed",
    "warning",
}


def dictionary_sentiment(text, positive_dict, negative_dict):
    """
    Calculate sentiment score using dictionary approach.
    Returns score between -1 (very negative) and +1 (very positive).
    """
    words = text.lower().split()

    pos_count = sum(1 for w in words if w in positive_dict)
    neg_count = sum(1 for w in words if w in negative_dict)

    total = pos_count + neg_count
    if total == 0:
        return 0.0

    # Normalized sentiment score
    score = (pos_count - neg_count) / total

    return score, pos_count, neg_count


# Analyze headlines
sentiment_results = []
for original, (processed, tickers) in zip(headlines, processed_headlines):
    score, pos, neg = dictionary_sentiment(
        processed, positive_words, negative_words
    )
    sentiment_results.append(
        {
            "headline": original[:40] + "...",
            "sentiment": score,
            "positive_words": pos,
            "negative_words": neg,
        }
    )
Out[20]:
Console
Dictionary-Based Sentiment Analysis:
----------------------------------------------------------------------
Apple beats Q3 earnings estimates, stock...
  Score: +1.00 (Positive)
  Positive words: 1, Negative words: 0

Fed signals rate cuts ahead, markets ral...
  Score: +1.00 (Positive)
  Positive words: 1, Negative words: 0

Tesla misses delivery targets, shares pl...
  Score: -1.00 (Negative)
  Positive words: 0, Negative words: 3

Goldman Sachs upgrades MSFT to buy, cite...
  Score: +1.00 (Positive)
  Positive words: 3, Negative words: 0

Oil prices crash as OPEC+ fails to reach...
  Score: -1.00 (Negative)
  Positive words: 0, Negative words: 1
Out[21]:
Visualization
Sentiment scores for five financial headlines using a dictionary-based approach. Headings related to earnings beats and analyst upgrades show strong positive scores, while production misses and price crashes generate significant negative values, demonstrating the model's ability to capture directional tone.
Sentiment scores for five financial headlines using a dictionary-based approach. Headings related to earnings beats and analyst upgrades show strong positive scores, while production misses and price crashes generate significant negative values, demonstrating the model's ability to capture directional tone.

Dictionary-based methods offer important advantages: they are transparent, fast, and require no training data. You can inspect the dictionary and understand exactly how the model reaches its conclusions. This interpretability is valuable for regulatory compliance and internal governance. However, these methods have significant limitations. They miss context entirely. The phrase "not profitable" contains a positive word ("profitable") but expresses negative sentiment through negation. Phrases like "exceeded expectations but guidance disappointed" contain both positive and negative elements that require understanding of sentence structure to interpret correctly. More sophisticated approaches are needed to capture these nuances.

Machine Learning Sentiment Models

Modern sentiment analysis uses machine learning models trained on labeled financial text. These models learn contextual patterns that dictionary methods miss, including negation handling, comparative constructions, and the subtle ways that sentiment is expressed in professional financial communication:

In[22]:
Code
from sklearn.pipeline import Pipeline
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB

# Create synthetic training data for demonstration
# In practice, you would use labeled datasets like Financial PhraseBank
training_texts = [
    "Company reports record profits and raises dividend",
    "Strong quarterly results exceed analyst expectations",
    "Revenue growth accelerates amid market expansion",
    "Management announces stock buyback program",
    "Earnings beat consensus estimates significantly",
    "Company misses revenue targets by wide margin",
    "Profit warning issued ahead of quarterly report",
    "Sales decline accelerates as competition intensifies",
    "Management cuts full year guidance substantially",
    "Restructuring charges lead to quarterly loss",
    "Market conditions remain challenging for growth",
    "Regulatory concerns weigh on stock performance",
    "Supply chain disruptions impact production capacity",
    "Debt levels raise concerns among analysts",
    "Customer losses accelerate amid service issues",
]
training_labels = [
    1,
    1,
    1,
    1,
    1,
    0,
    0,
    0,
    0,
    0,
    0,
    0,
    0,
    0,
    0,
]  # 1=positive, 0=negative

# Build sentiment classification pipeline
sentiment_pipeline = Pipeline(
    [
        ("tfidf", TfidfVectorizer(ngram_range=(1, 2), max_features=500)),
        ("classifier", MultinomialNB(alpha=0.1)),
    ]
)

sentiment_pipeline.fit(training_texts, training_labels)

# Analyze new headlines
ml_predictions = []
for original, (processed, tickers) in zip(headlines, processed_headlines):
    prob = sentiment_pipeline.predict_proba([processed])[0]
    ml_predictions.append(
        {
            "headline": original[:40] + "...",
            "negative_prob": prob[0],
            "positive_prob": prob[1],
            "prediction": "Positive" if prob[1] > 0.5 else "Negative",
        }
    )
Out[23]:
Console
ML-Based Sentiment Analysis:
----------------------------------------------------------------------
Apple beats Q3 earnings estimates, stock...
  Prediction: Positive
  Confidence - Positive: 86.7%, Negative: 13.3%

Fed signals rate cuts ahead, markets ral...
  Prediction: Negative
  Confidence - Positive: 8.9%, Negative: 91.1%

Tesla misses delivery targets, shares pl...
  Prediction: Negative
  Confidence - Positive: 8.5%, Negative: 91.5%

Goldman Sachs upgrades MSFT to buy, cite...
  Prediction: Negative
  Confidence - Positive: 24.6%, Negative: 75.4%

Oil prices crash as OPEC+ fails to reach...
  Prediction: Negative
  Confidence - Positive: 8.7%, Negative: 91.3%

The machine learning model captures nuances that simple keyword matching would miss. By learning from examples of financial text labeled with sentiment, the model develops internal representations that go beyond individual words. It learns that "misses targets" signals negative sentiment even without the word "bad," and that "raises dividend" implies confidence in future cash flows. The TF-IDF vectorization with bigrams helps here, because phrases like "misses targets" or "raises dividend" are captured as single features rather than independent words.

Production sentiment systems typically use more sophisticated architectures, including deep learning models like BERT and its financial variants (FinBERT), which understand context through attention mechanisms that can weigh the importance of different parts of the text. These models can handle complex sentences with multiple sentiment-bearing clauses, correctly parsing constructions like "despite strong revenue growth, margins contracted significantly" as mixed or negative overall.

Aggregating Sentiment Signals

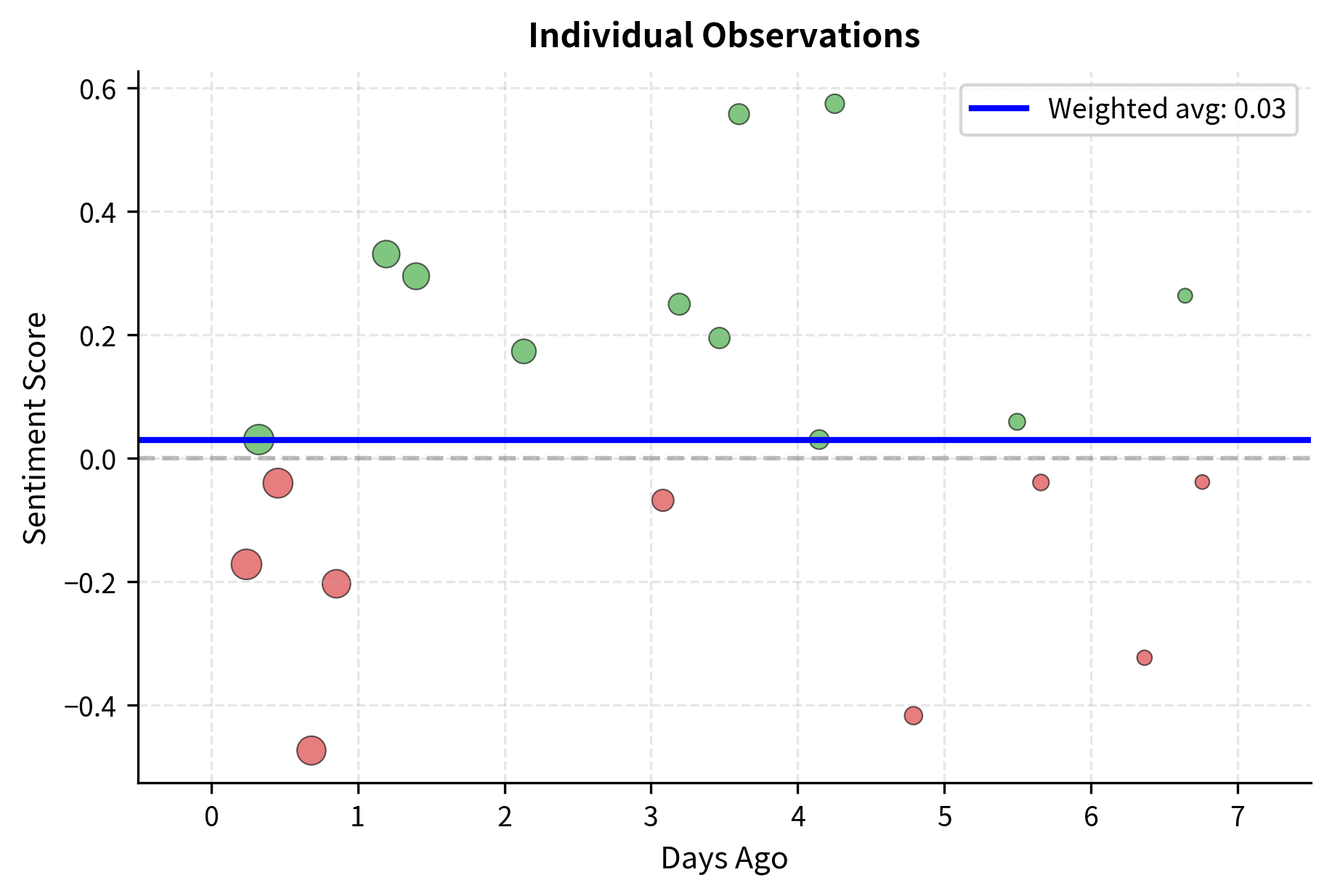
Individual sentiment scores must be aggregated into tradable signals. A single news article provides limited information, but the collective sentiment across all coverage of a company tells a more complete story. Common approaches include time-weighted averages (more recent information matters more), volume-weighted sentiment (high-profile sources like the Wall Street Journal get more weight than obscure blogs), and sentiment momentum (changes in sentiment level):

In[24]:
Code
def aggregate_sentiment_signals(sentiment_scores, timestamps, decay_halflife=3):
    """
    Aggregate multiple sentiment observations into a single signal.
    Uses exponential decay weighting: more recent observations matter more.

    Parameters:

    - sentiment_scores: Array of individual sentiment scores
    - timestamps: Array of observation times (in days relative to now)
    - decay_halflife: Half-life for exponential decay in days
    """
    # Calculate decay weights
    decay_rate = np.log(2) / decay_halflife
    weights = np.exp(-decay_rate * timestamps)
    weights = weights / weights.sum()  # Normalize

    # Weighted average sentiment
    weighted_sentiment = np.sum(sentiment_scores * weights)

    # Sentiment dispersion (disagreement)
    sentiment_std = np.sqrt(
        np.sum(weights * (sentiment_scores - weighted_sentiment) ** 2)
    )

    # Sentiment momentum: compare recent vs older
    recent_mask = timestamps <= decay_halflife
    if recent_mask.sum() > 0 and (~recent_mask).sum() > 0:
        recent_sentiment = sentiment_scores[recent_mask].mean()
        older_sentiment = sentiment_scores[~recent_mask].mean()
        sentiment_momentum = recent_sentiment - older_sentiment
    else:
        sentiment_momentum = 0.0

    return {
        "aggregate_sentiment": weighted_sentiment,
        "sentiment_dispersion": sentiment_std,
        "sentiment_momentum": sentiment_momentum,
    }


# Example: aggregate sentiment for a stock over past week
np.random.seed(42)
n_observations = 20
sentiment_scores = np.random.normal(
    0.1, 0.3, n_observations
)  # Slightly positive on average
timestamps = np.random.uniform(0, 7, n_observations)  # Days ago

aggregated = aggregate_sentiment_signals(sentiment_scores, timestamps)
Out[25]:
Console
Aggregated Sentiment Signal:
  Weighted Sentiment: +0.029
  Sentiment Dispersion: 0.276
  Sentiment Momentum: -0.094

  - Sentiment is neutral
  - High disagreement among sources (lower conviction)
Out[26]:
Visualization
Individual sentiment observations overlaid with their decay weights. Recent news items (larger points) exert greater influence on the aggregate signal than older information.
Individual sentiment observations overlaid with their decay weights. Recent news items (larger points) exert greater influence on the aggregate signal than older information.
Out[27]:
Visualization
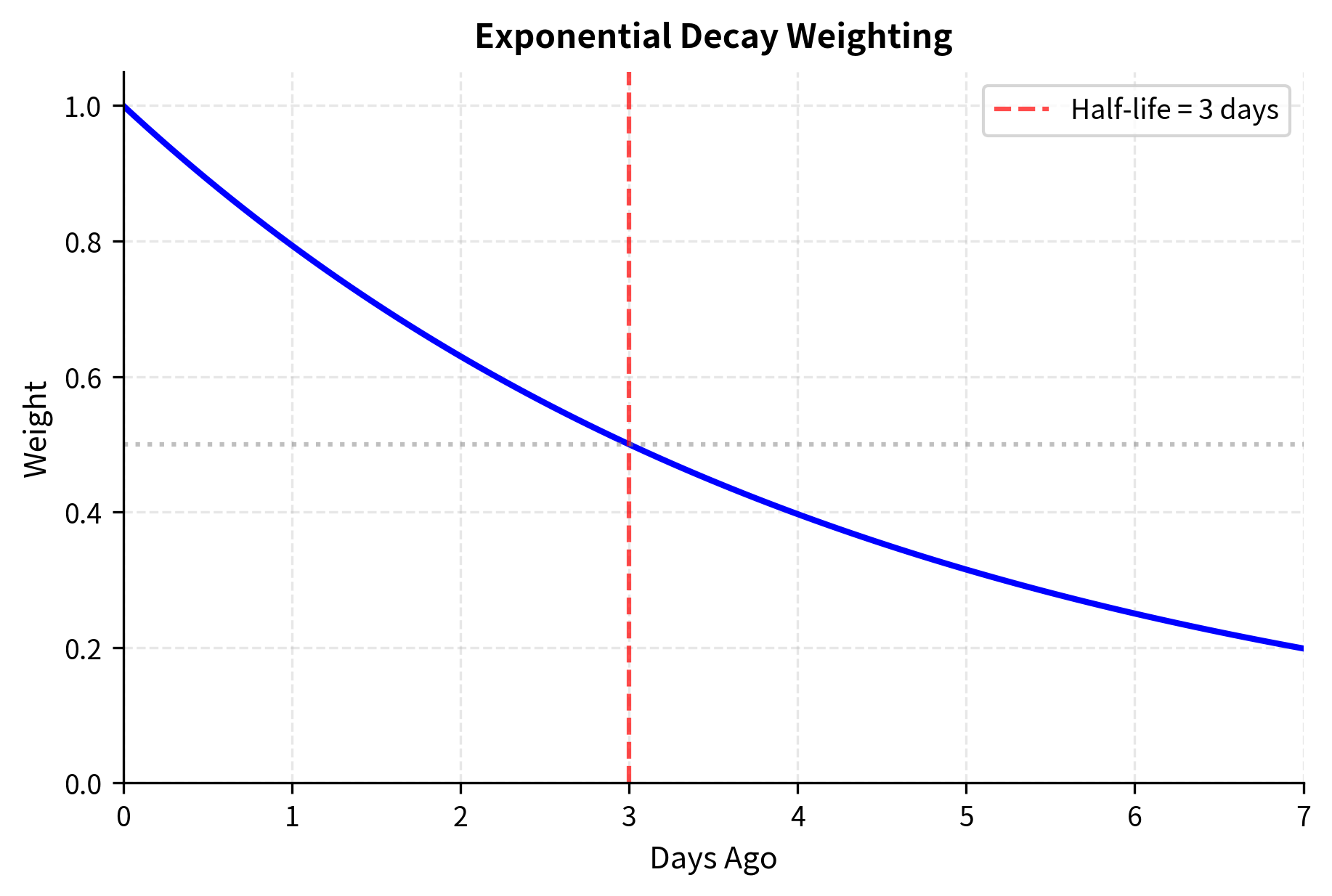
Exponential decay weighting function for sentiment aggregation. The half-life of 3 days ensures the signal remains responsive to new information while smoothing out transient noise.
Exponential decay weighting function for sentiment aggregation. The half-life of 3 days ensures the signal remains responsive to new information while smoothing out transient noise.

By systematically aggregating signals across multiple sources and time periods, we transform noisy individual data points into a coherent market view. The exponential decay weighting ensures that yesterday's news matters more than last week's, reflecting how information gets incorporated into prices over time. The sentiment dispersion metric captures an often-overlooked dimension: when sources disagree widely, the signal is less reliable than when there's consensus. A stock with uniformly positive coverage provides a stronger buy signal than one with mixed reviews, even if the average sentiment is similar. The momentum component adds yet another layer, capturing whether sentiment is improving or deteriorating. A company with moderately positive sentiment that's improving may be more attractive than one with strongly positive sentiment that's declining.

Key Parameters

The key parameters for the sentiment analysis pipeline are:

  • ngram_range: The range of n-grams (word sequences) to extract. Including bigrams (pairs of words) captures context better than single words alone.
  • max_features: The maximum number of words to include in the vocabulary. Limiting this focuses the model on the most frequent and informative terms.
  • alpha: The smoothing parameter for Naive Bayes. It prevents the model from assigning zero probability to words not seen in the training data.

The next chapter provides a deeper exploration of NLP techniques and alternative data sources, including more sophisticated approaches like transformer-based models and entity extraction.

Alternative Data in Trading Strategies

Alternative data refers to information sources beyond traditional market data and financial statements. Satellite imagery of parking lots, credit card transaction data, web traffic statistics, and shipping container movements can all provide insights into economic activity before it appears in official reports. This data advantage creates alpha when incorporated into trading strategies.

The fundamental insight behind alternative data is that traditional financial metrics, like quarterly earnings reports, are inherently backward-looking and delayed. By the time a company reports revenue growth, the activities generating that revenue occurred weeks or months earlier. Alternative data sources can observe those activities in real-time, providing a preview of what official numbers will eventually show. A fund that can accurately estimate retail sales from credit card data has information that won't appear in public filings for months.

Categories of Alternative Data

Alternative data sources fall into several categories, each with distinct characteristics, coverage, and analytical requirements:

Geospatial data includes satellite and drone imagery used to monitor retail foot traffic, oil storage levels, agricultural yields, and construction activity. A classic example is counting cars in Walmart parking lots to predict quarterly revenue before earnings announcements. Modern computer vision algorithms can automatically process thousands of satellite images daily, counting vehicles, measuring shadow lengths on oil tanks (to estimate fill levels), and assessing crop health from vegetation indices. This data provides direct observation of physical economic activity that eventually flows through to financial statements.

Transaction data encompasses credit card purchases, point-of-sale data, and electronic receipts. These provide real-time views of consumer spending patterns at individual company and sector levels. When a new iPhone launches, credit card data can reveal sales volumes within days, long before Apple reports quarterly results. The granularity is remarkable: analysts can track spending by geography, demographics, and product category. The main limitation is coverage, since any single data provider sees only a fraction of total transactions.

Web and social data includes search trends, app downloads, social media mentions, and website traffic. Surging search interest in a product can predict sales growth, while declining app engagement might signal user attrition before it appears in subscriber counts. Social media sentiment can indicate brand health, customer satisfaction, or emerging crises. Google Trends data, for instance, has been shown to predict earnings surprises for retail companies based on search interest in brand names.

Sensor and IoT data covers supply chain sensors, energy consumption metrics, and industrial equipment monitoring. Real-time shipping data can reveal supply chain disruptions before they impact earnings. Power consumption at manufacturing facilities can indicate production volumes. Fleet tracking data can show logistics efficiency. As more industrial equipment becomes connected, the volume and value of this data category continues to grow.

In[28]:
Code
# Simulate alternative data integration
import numpy as np
import pandas as pd

np.random.seed(42)

# Create synthetic alt data that leads market by 5 days
n_periods = 500
dates = pd.date_range("2020-01-01", periods=n_periods, freq="B")

# True underlying economic activity (unobserved)
economic_activity = np.cumsum(np.random.normal(0.001, 0.02, n_periods))

# Stock returns follow economic activity with noise
stock_returns = np.diff(economic_activity) + np.random.normal(
    0, 0.015, n_periods - 1
)
stock_returns = np.insert(stock_returns, 0, 0)

# Alternative data: credit card spending (leads economic activity by ~5 days)
alt_data_noise = np.random.normal(0, 0.3, n_periods)
credit_card_spending = np.roll(economic_activity, -5) + alt_data_noise

# Traditional data: reported revenues (lags by ~20 days)
traditional_data_noise = np.random.normal(0, 0.2, n_periods)
reported_revenues = np.roll(economic_activity, 20) + traditional_data_noise

alt_data_df = pd.DataFrame(
    {
        "date": dates,
        "stock_return": stock_returns,
        "credit_card_spending": credit_card_spending,
        "reported_revenues": reported_revenues,
        "economic_activity": economic_activity,
    }
).set_index("date")
In[29]:
Code
# Calculate correlations at different lags
max_lag = 30
lags = range(-max_lag, max_lag + 1)
cc_corrs = []
trad_corrs = []

for lag in lags:
    if lag >= 0:
        cc_corr = np.corrcoef(
            alt_data_df["credit_card_spending"].iloc[lag:],
            alt_data_df["economic_activity"].iloc[:-lag]
            if lag > 0
            else alt_data_df["economic_activity"],
        )[0, 1]
        trad_corr = np.corrcoef(
            alt_data_df["reported_revenues"].iloc[lag:],
            alt_data_df["economic_activity"].iloc[:-lag]
            if lag > 0
            else alt_data_df["economic_activity"],
        )[0, 1]
    else:
        cc_corr = np.corrcoef(
            alt_data_df["credit_card_spending"].iloc[:lag],
            alt_data_df["economic_activity"].iloc[-lag:],
        )[0, 1]
        trad_corr = np.corrcoef(
            alt_data_df["reported_revenues"].iloc[:lag],
            alt_data_df["economic_activity"].iloc[-lag:],
        )[0, 1]
    cc_corrs.append(cc_corr)
    trad_corrs.append(trad_corr)
In[30]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Plot the signals
plt.figure()
start_idx, end_idx = 50, 200
subset = alt_data_df.iloc[start_idx:end_idx]

plt.plot(
    subset.index,
    subset["economic_activity"],
    "k-",
    linewidth=2,
    label="True Economic Activity",
)
plt.plot(
    subset.index,
    subset["credit_card_spending"],
    "g--",
    alpha=0.7,
    label="Credit Card Data (leads)",
)
plt.plot(
    subset.index,
    subset["reported_revenues"],
    "r:",
    alpha=0.7,
    label="Reported Revenues (lags)",
)
plt.ylabel("Activity Level")
plt.title("Alternative Data Timing Advantage")
plt.legend()
plt.show()
Out[30]:
Visualization
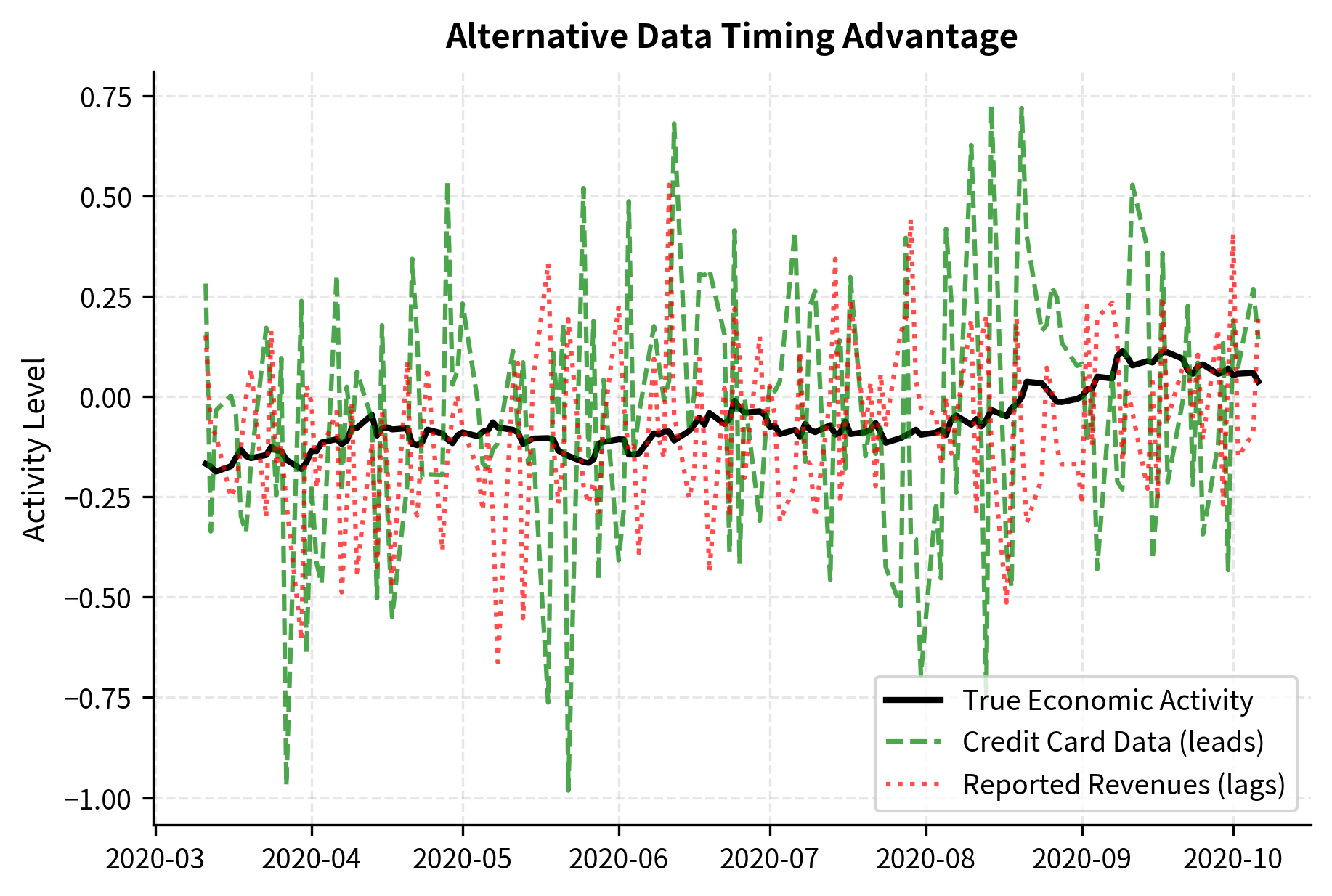
Time series plot showing credit card spending leading economic activity and reported revenues lagging.
Time series comparison of economic activity indicators. Credit card spending (green) leads the underlying economic activity, while reported revenues (red) lag due to reporting delays.
In[31]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

plt.figure()
plt.plot(lags, cc_corrs, "g-", linewidth=2, label="Credit Card Data")
plt.plot(lags, trad_corrs, "r-", linewidth=2, label="Reported Revenues")
plt.axvline(x=0, color="k", linestyle="--", alpha=0.3)
plt.xlabel("Lag (days, negative = leads)")
plt.ylabel("Correlation with Economic Activity")
plt.title("Lead-Lag Relationship with Underlying Activity")
plt.legend()
plt.show()
Out[31]:
Visualization
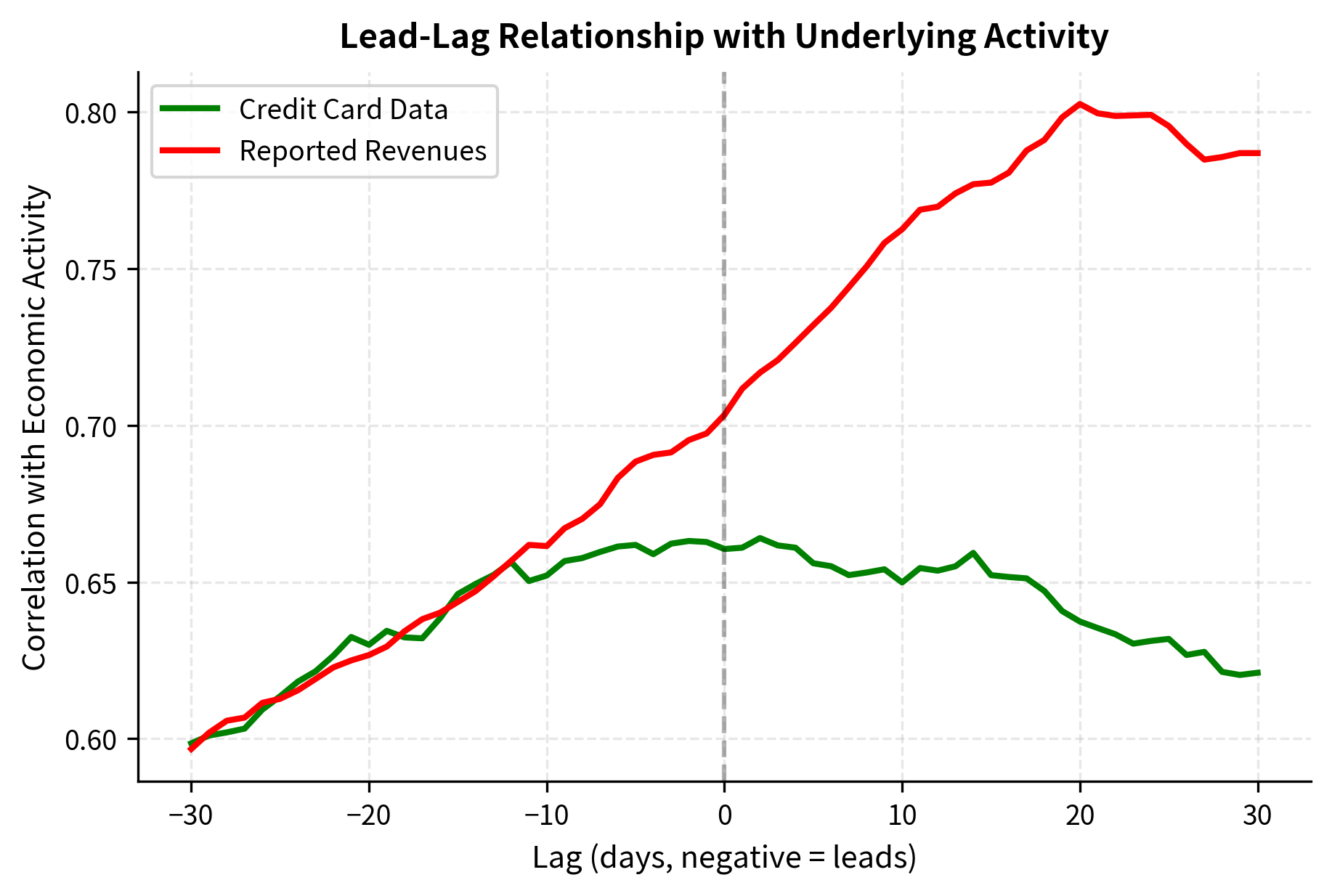
Cross-correlation analysis of credit card data and reported revenues against underlying economic activity. Credit card data (green) exhibits peak correlation at negative lags, confirming it as a leading indicator, whereas reported revenues (red) peak at positive lags due to reporting delays. This timing differential provides the predictive edge in the alternative data model.
Cross-correlation analysis of credit card data and reported revenues against underlying economic activity. Credit card data (green) exhibits peak correlation at negative lags, confirming it as a leading indicator, whereas reported revenues (red) peak at positive lags due to reporting delays. This timing differential provides the predictive edge in the alternative data model.

The lead-lag analysis demonstrates visually why alternative data commands premium pricing in the financial industry. Credit card data correlates with economic activity at negative lags, meaning it leads: when we observe credit card spending today, it tells us about economic activity that will be reflected in stock prices over the coming days. Traditional reported data correlates at positive lags, meaning it lags: by the time quarterly revenues are reported, the market has already moved to reflect the underlying activity. This timing advantage can translate into significant trading alpha because you're trading on information that other market participants don't yet have.

Incorporating Alternative Data into Models

Alternative data must be carefully integrated with traditional features. The process involves several key challenges. First, different data sources update at different frequencies: credit card data might be daily, satellite imagery weekly, and reported revenues quarterly. Second, data quality varies dramatically across providers and time periods. Third, there's a significant risk of data snooping: with hundreds of potential alternative data sources, some will appear predictive by chance, and selecting which sources to use based on historical performance can create dangerous overfitting.

In[32]:
Code
def create_combined_features(df, alt_data_cols, traditional_cols):
    """
    Create feature set combining alternative and traditional data.
    Handles different data frequencies and missing values.
    """
    features = pd.DataFrame(index=df.index)

    # Alternative data features
    for col in alt_data_cols:
        # Current level
        features[f"{col}_level"] = df[col]
        # Rate of change
        features[f"{col}_change_5d"] = df[col].diff(5)
        # Z-score (deviation from recent mean)
        features[f"{col}_zscore"] = (df[col] - df[col].rolling(21).mean()) / df[
            col
        ].rolling(21).std()

    # Traditional data features
    for col in traditional_cols:
        features[f"{col}_level"] = df[col]
        features[f"{col}_change_21d"] = df[col].diff(21)

    # Interaction features: alternative data relative to traditional
    if len(alt_data_cols) > 0 and len(traditional_cols) > 0:
        alt_col = alt_data_cols[0]
        trad_col = traditional_cols[0]
        features["alt_vs_trad_spread"] = (
            features[f"{alt_col}_zscore"]
            - (df[trad_col] - df[trad_col].rolling(21).mean())
            / df[trad_col].rolling(21).std()
        )

    return features


# Create combined feature set
combined_features = create_combined_features(
    alt_data_df,
    alt_data_cols=["credit_card_spending"],
    traditional_cols=["reported_revenues"],
)

# Prepare data for modeling
combined_features["target"] = (
    alt_data_df["stock_return"].shift(-1) > 0
).astype(int)
model_data = combined_features.dropna()

# Train-test split
split_point = int(len(model_data) * 0.7)
train = model_data.iloc[:split_point]
test = model_data.iloc[split_point:]

feature_names = [c for c in combined_features.columns if c != "target"]
In[33]:
Code
# Compare model performance with and without alternative data

# Model using only traditional data
trad_features = [c for c in feature_names if "reported" in c]
rf_trad = RandomForestClassifier(n_estimators=100, max_depth=4, random_state=42)
rf_trad.fit(train[trad_features], train["target"])
pred_trad = rf_trad.predict_proba(test[trad_features])[:, 1]
auc_trad = roc_auc_score(test["target"], pred_trad)

# Model using alternative data
alt_features = [c for c in feature_names if "credit_card" in c]
rf_alt = RandomForestClassifier(n_estimators=100, max_depth=4, random_state=42)
rf_alt.fit(train[alt_features], train["target"])
pred_alt = rf_alt.predict_proba(test[alt_features])[:, 1]
auc_alt = roc_auc_score(test["target"], pred_alt)

# Combined model
rf_combined = RandomForestClassifier(
    n_estimators=100, max_depth=4, random_state=42
)
rf_combined.fit(train[feature_names], train["target"])
pred_combined = rf_combined.predict_proba(test[feature_names])[:, 1]
auc_combined = roc_auc_score(test["target"], pred_combined)
Out[34]:
Console
Model Performance Comparison (AUC-ROC):
---------------------------------------------
Traditional Data Only:    0.4373
Alternative Data Only:    0.4799
Combined Model:           0.4681

Alternative Data Lift:    +9.7%
Combined vs Traditional:  +7.0%
Out[35]:
Visualization
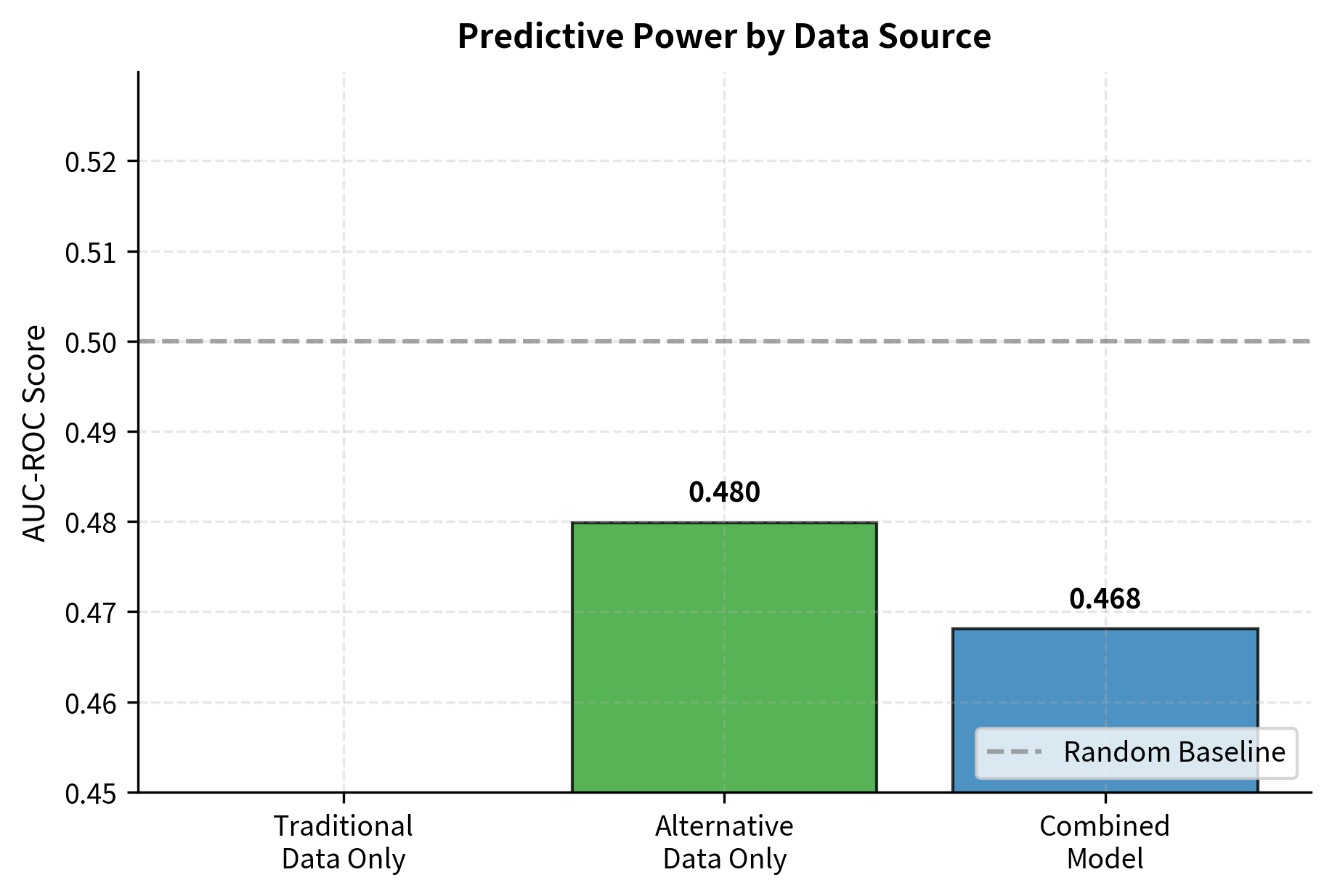
Predictive performance (AUC-ROC) comparison across data sources. The alternative data model outperforms the traditional data model due to its timing advantage, while combining both sources yields the highest predictive power.
Predictive performance (AUC-ROC) comparison across data sources. The alternative data model outperforms the traditional data model due to its timing advantage, while combining both sources yields the highest predictive power.

The alternative data model outperforms the traditional data model due to its information timing advantage. By the time traditional metrics are available, much of their informational content has already been reflected in prices. Alternative data captures the same underlying economic activity but with a crucial head start. The combined model often provides incremental improvement over either source alone by capturing both leading signals (from alternative data) and confirming signals (from traditional data). When credit card spending suggests strong sales and reported revenues eventually confirm that strength, the convergence of evidence strengthens conviction.

Key Parameters

The key parameters for integrating alternative data are:

  • Lookback Window: The period used for calculating trends and z-scores (e.g., 21 days). This should match the frequency of the alternative data.
  • Lag: The time delay applied to align data series. Correctly aligning leading alternative data with lagging market data is critical for extracting alpha.
  • n_estimators: The number of trees in the Random Forest. Sufficient trees are needed to capture interactions between alternative and traditional features.

Unsupervised Learning for Market Structure

Not all valuable patterns require labeled data. Unsupervised learning techniques discover hidden structure in market data without being told what to look for. These methods excel at grouping similar assets, identifying regime changes, and detecting anomalies that signal risk or opportunity. The absence of labels forces these algorithms to find patterns based on the intrinsic structure of the data, often revealing relationships that wouldn't be apparent from traditional analysis.

Clustering for Portfolio Construction

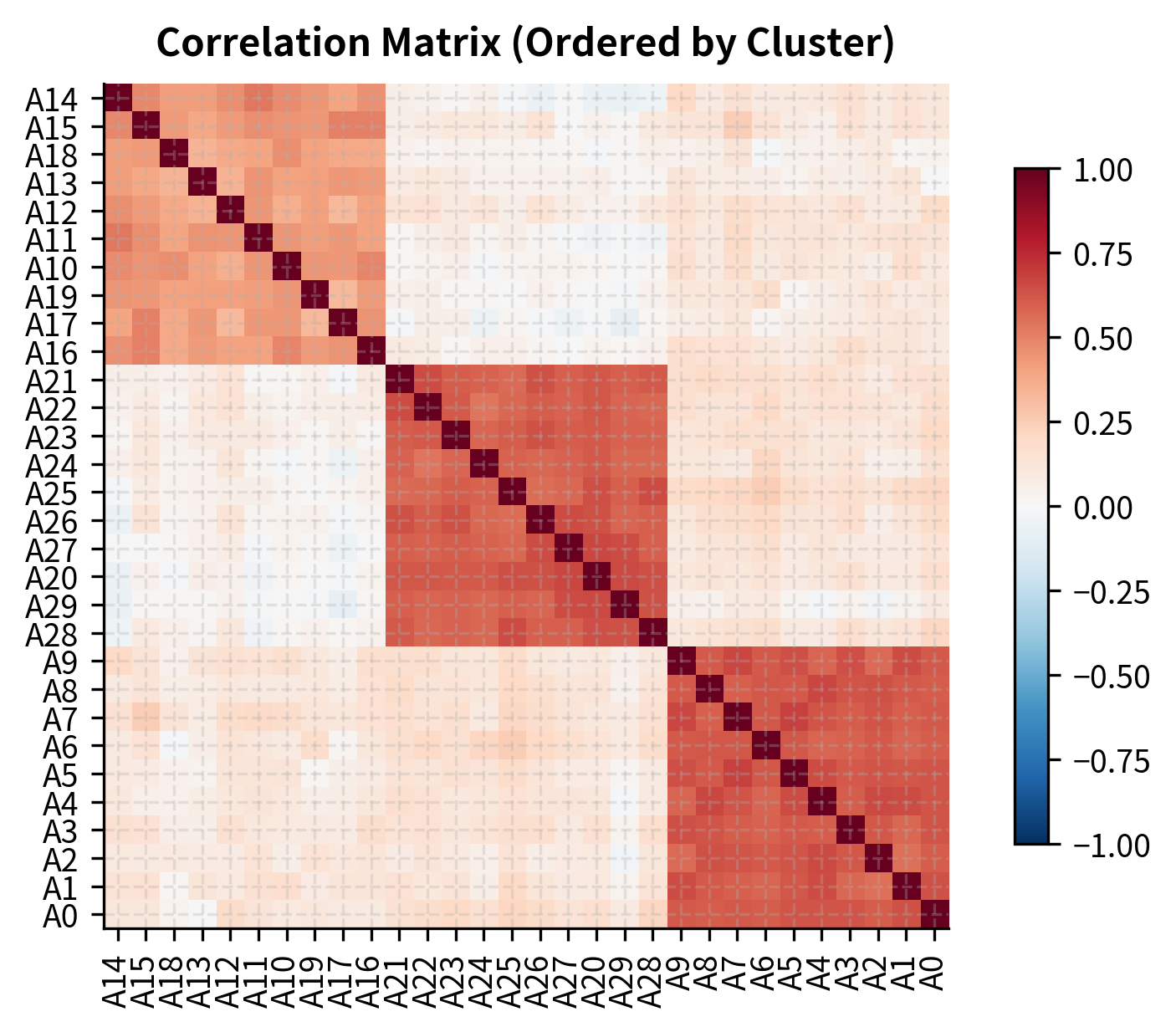
Hierarchical clustering and k-means provide data-driven alternatives to traditional sector classifications. Standard industry categories, like GICS sectors or NAICS codes, group companies based on what they do. But for portfolio construction, what matters is how assets behave together in the market, their return correlations and factor exposures. Two tech companies in the same GICS sector might have very different risk profiles if one is a growth stock sensitive to interest rates while the other is a mature value play.

Assets grouped by return covariance patterns may reveal economic relationships that standard industry categories miss. A cloud computing company might cluster more closely with commercial real estate (both sensitive to business investment cycles) than with social media companies (more dependent on advertising spending). By letting the data determine groupings, clustering can identify these unexpected but economically meaningful relationships:

In[36]:
Code
import numpy as np
import pandas as pd

# Generate synthetic multi-asset returns with cluster structure
np.random.seed(42)
n_assets = 30
n_days = 252

# Create factor returns
tech_factor = np.random.normal(0.0005, 0.015, n_days)
value_factor = np.random.normal(0.0003, 0.012, n_days)
defensive_factor = np.random.normal(0.0002, 0.008, n_days)
market_factor = np.random.normal(0.0003, 0.01, n_days)

# Assign assets to clusters with varying factor exposures
asset_returns = np.zeros((n_days, n_assets))
cluster_assignments_true = []

for i in range(n_assets):
    if i < 10:  # Tech-like assets
        asset_returns[:, i] = (
            0.8 * tech_factor
            + 0.5 * market_factor
            + np.random.normal(0, 0.01, n_days)
        )
        cluster_assignments_true.append(0)
    elif i < 20:  # Value-like assets
        asset_returns[:, i] = (
            0.7 * value_factor
            + 0.6 * market_factor
            + np.random.normal(0, 0.012, n_days)
        )
        cluster_assignments_true.append(1)
    else:  # Defensive assets
        asset_returns[:, i] = (
            0.9 * defensive_factor
            + 0.3 * market_factor
            + np.random.normal(0, 0.006, n_days)
        )
        cluster_assignments_true.append(2)

returns_df = pd.DataFrame(
    asset_returns, columns=[f"Asset_{i}" for i in range(n_assets)]
)

# Calculate correlation matrix
corr_matrix = returns_df.corr()
In[37]:
Code
from scipy.cluster.hierarchy import linkage
from scipy.spatial.distance import squareform
from sklearn.cluster import KMeans

# Perform hierarchical clustering on correlation distance
# Convert correlation to distance: d = sqrt(0.5 * (1 - corr))
distance_matrix = np.sqrt(0.5 * (1 - corr_matrix))

# Hierarchical clustering
linkage_matrix = linkage(squareform(distance_matrix), method="ward")

# K-means on return features (using covariance-based features)
cov_features = corr_matrix.values  # Use correlation profile as features
kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels = kmeans.fit_predict(cov_features)
In[38]:
Code
from scipy.cluster.hierarchy import dendrogram
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Dendrogram
plt.figure()
dendrogram(
    linkage_matrix,
    labels=[f"A{i}" for i in range(n_assets)],
    leaf_rotation=90,
    leaf_font_size=9,
)
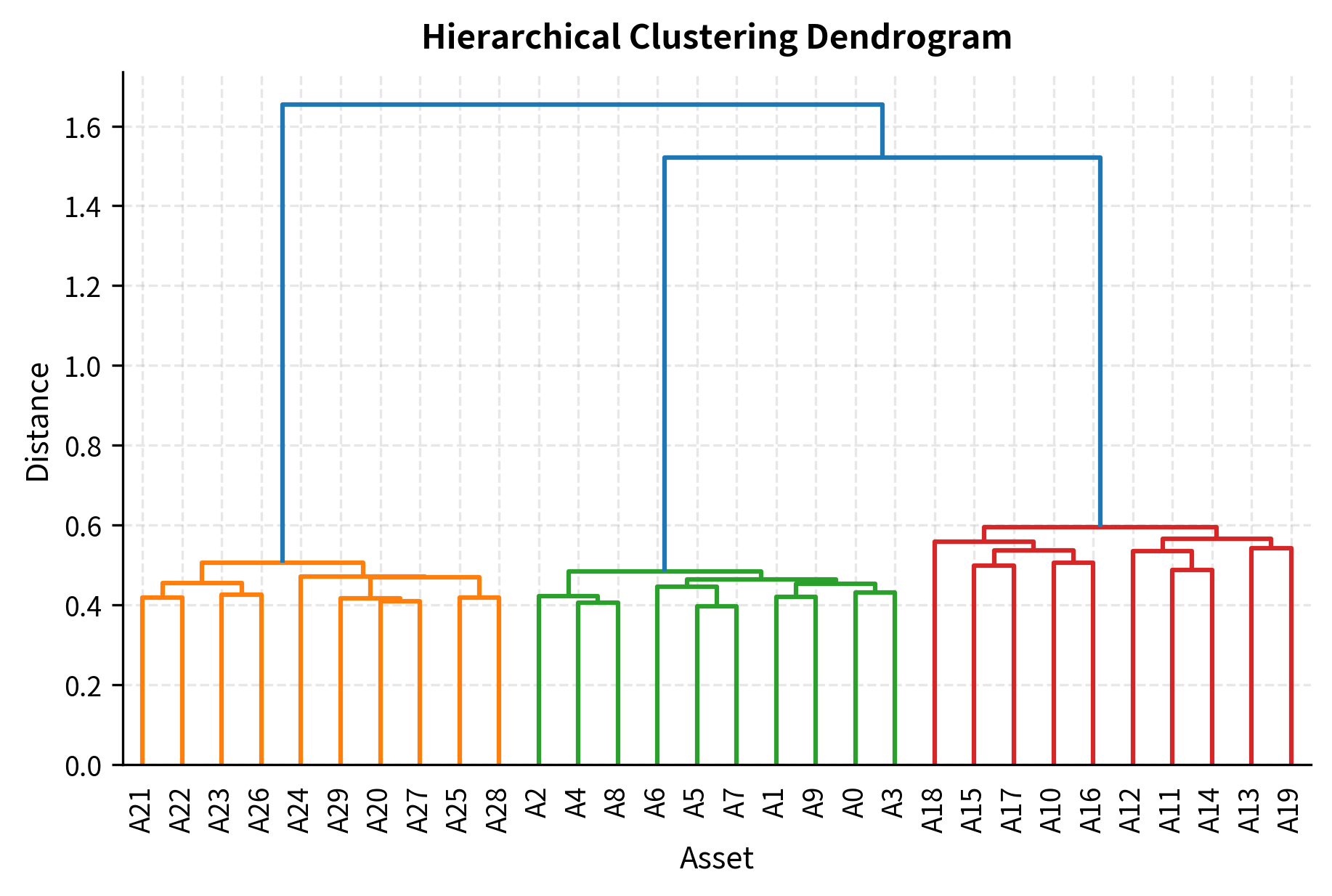
plt.title("Hierarchical Clustering Dendrogram")
plt.xlabel("Asset")
plt.ylabel("Distance")
plt.show()
Out[38]:
Visualization
Hierarchical clustering dendrogram.
Dendrogram from hierarchical clustering of 30 synthetic assets based on return correlations. The tree structure illustrates the proximity of assets within tech, value, and defensive groups, providing a data-driven basis for portfolio diversification.
In[39]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Reorder correlation matrix by cluster
plt.figure()
cluster_order = np.argsort(cluster_labels)
ordered_corr = corr_matrix.iloc[cluster_order, cluster_order]

im = plt.imshow(ordered_corr, cmap="RdBu_r", vmin=-1, vmax=1)
plt.title("Correlation Matrix (Ordered by Cluster)")
plt.xticks(range(n_assets), [f"A{i}" for i in cluster_order], rotation=90)
plt.yticks(range(n_assets), [f"A{i}" for i in cluster_order])
plt.colorbar(im, shrink=0.8)
plt.show()
Out[39]:
Visualization
Clustered correlation heatmap.
Correlation matrix reordered by cluster membership. The block-diagonal structure highlights groups of highly correlated assets (red blocks) separated by lower correlations.
In[40]:
Code
from sklearn.metrics import adjusted_rand_score

ari = adjusted_rand_score(cluster_assignments_true, cluster_labels)
Out[41]:
Console
Clustering Quality:
  Adjusted Rand Index: 1.000 (1.0 = perfect match with true clusters)

Cluster Composition:
  Cluster 0: 10 assets - ['A10', 'A11', 'A12', 'A13', 'A14']...
  Cluster 1: 10 assets - ['A20', 'A21', 'A22', 'A23', 'A24']...
  Cluster 2: 10 assets - ['A0', 'A1', 'A2', 'A3', 'A4']...

The clustering identifies natural groupings in the data that can inform portfolio construction. The dendrogram on the left shows the hierarchical structure of asset relationships: assets that merge at lower heights are more similar, while those that only join at the top of the tree are quite different. The correlation heatmap on the right, reordered by cluster membership, reveals the block structure that clustering uncovers. Within each block (cluster), correlations are high, indicating that these assets move together. Between blocks, correlations are lower, suggesting genuine diversification potential.

Rather than using arbitrary sector classifications that may not reflect current market dynamics, you can build diversified portfolios by selecting assets from different clusters. This approach ensures genuine diversification of risk exposures based on how assets actually behave, not how they're categorized. When correlations change (as they often do during market stress), the clusters can be recomputed to maintain effective diversification.

Anomaly Detection for Risk Management

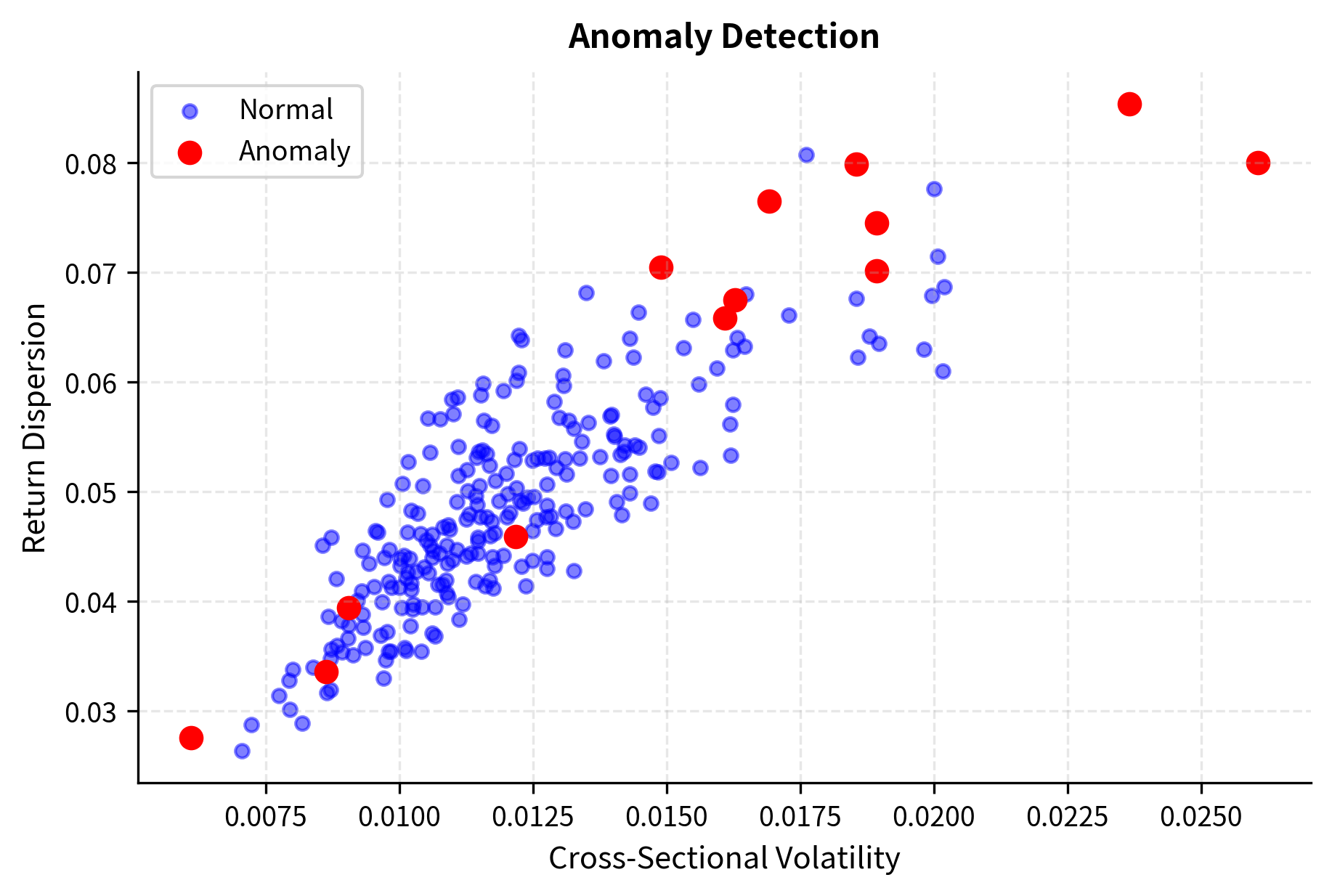
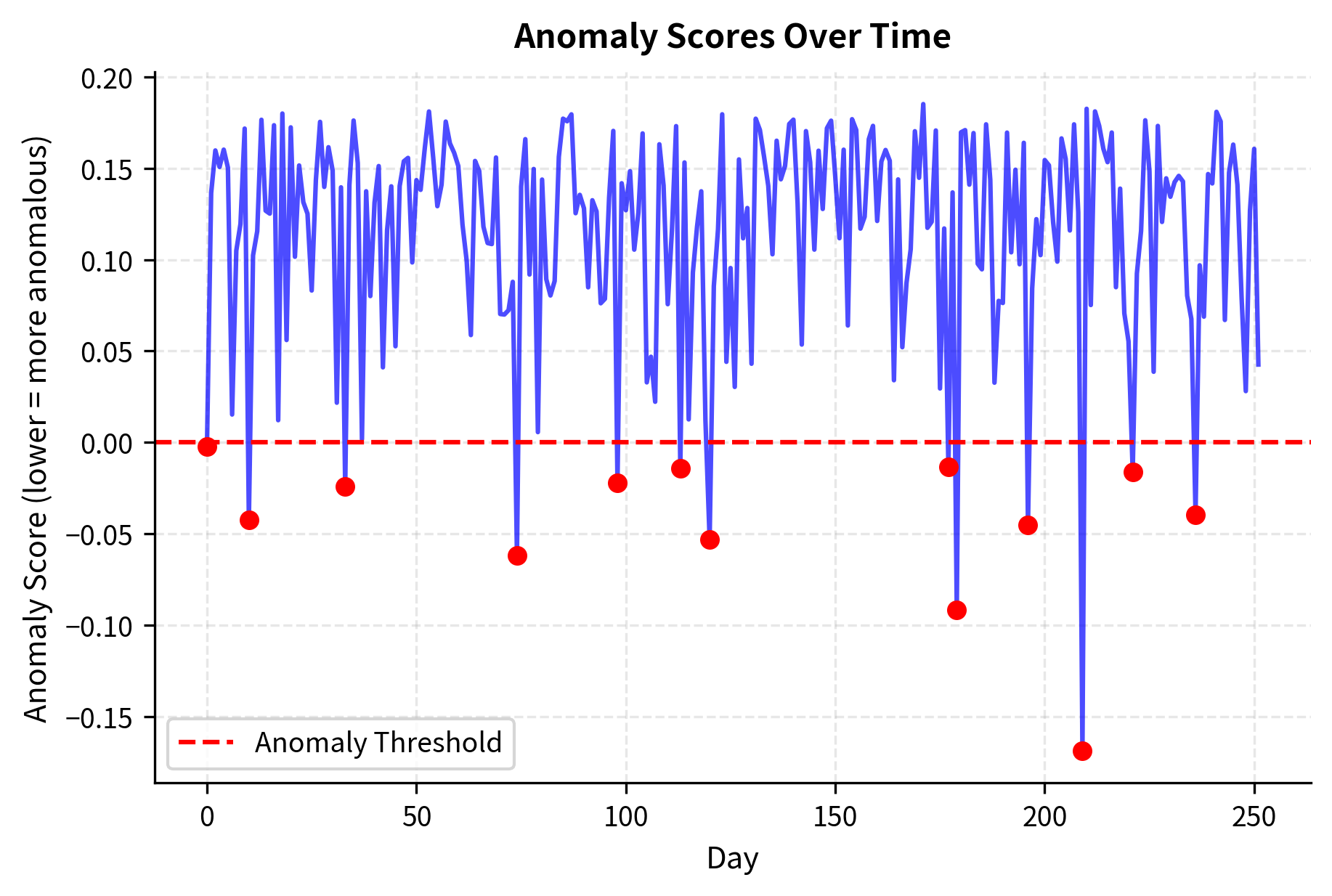
Unsupervised anomaly detection identifies unusual market behavior that might signal emerging risks or trading opportunities. The logic is that normal market conditions, while noisy, exhibit statistical regularities. When these regularities break down, when volatility spikes unexpectedly, when correlations shift dramatically, when the distribution of returns changes character, something unusual is happening. Detecting these anomalies early can help traders manage risk or capitalize on dislocations.

Isolation forests and autoencoders are particularly effective for high-dimensional financial data. Isolation forests work by recursively partitioning data; points that can be isolated quickly (with few partitions) are anomalous because they're far from the dense regions where most data lies. This approach is computationally efficient and doesn't require assumptions about the distribution of normal data:

In[42]:
Code
from sklearn.ensemble import IsolationForest


def detect_market_anomalies(returns_df, contamination=0.05):
    """
    Detect anomalous market conditions using Isolation Forest.

    Parameters:

    - returns_df: DataFrame of asset returns
    - contamination: Expected proportion of anomalies

    Returns:

    - anomaly_scores: Lower = more anomalous
    - anomaly_labels: -1 for anomalies, 1 for normal
    """
    # Create cross-sectional features for each day
    daily_features = pd.DataFrame(index=returns_df.index)
    daily_features["cross_sectional_mean"] = returns_df.mean(axis=1)
    daily_features["cross_sectional_std"] = returns_df.std(axis=1)
    daily_features["cross_sectional_skew"] = returns_df.skew(axis=1)
    daily_features["pct_positive"] = (returns_df > 0).mean(axis=1)
    daily_features["dispersion"] = returns_df.max(axis=1) - returns_df.min(
        axis=1
    )

    # Isolation Forest
    iso_forest = IsolationForest(contamination=contamination, random_state=42)
    anomaly_labels = iso_forest.fit_predict(daily_features)
    anomaly_scores = iso_forest.decision_function(daily_features)

    return daily_features, anomaly_scores, anomaly_labels


daily_features, anomaly_scores, anomaly_labels = detect_market_anomalies(
    returns_df
)
In[43]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Scatter of features colored by anomaly status
plt.figure()
normal_mask = anomaly_labels == 1
plt.scatter(
    daily_features.loc[normal_mask, "cross_sectional_std"],
    daily_features.loc[normal_mask, "dispersion"],
    c="blue",
    alpha=0.5,
    s=20,
    label="Normal",
)
plt.scatter(
    daily_features.loc[~normal_mask, "cross_sectional_std"],
    daily_features.loc[~normal_mask, "dispersion"],
    c="red",
    s=50,
    label="Anomaly",
)
plt.xlabel("Cross-Sectional Volatility")
plt.ylabel("Return Dispersion")
plt.title("Anomaly Detection")
plt.legend()
plt.show()
Out[43]:
Visualization
Scatter plot of cross-sectional volatility versus dispersion with anomalies highlighted in red.
Anomaly detection in the volatility-dispersion plane using an Isolation Forest. Normal market behavior (blue) clusters in a central region, while anomalies (red) appear as outliers with extreme volatility or dispersion, signaling potential market dislocations or data errors.
In[44]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Anomaly scores over time
plt.figure()
plt.plot(range(len(anomaly_scores)), anomaly_scores, "b-", alpha=0.7)
plt.axhline(y=0, color="r", linestyle="--", label="Anomaly Threshold")
anomaly_days = np.where(anomaly_labels == -1)[0]
plt.scatter(anomaly_days, anomaly_scores[anomaly_days], c="red", s=30, zorder=5)
plt.xlabel("Day")
plt.ylabel("Anomaly Score (lower = more anomalous)")
plt.title("Anomaly Scores Over Time")
plt.legend()
plt.show()
Out[44]:
Visualization
Time series of anomaly scores generated by the Isolation Forest. Sharp dips below the red dashed threshold line indicate statistically significant anomalies, flagging potential market dislocations or data quality issues that require risk management attention.
Time series of anomaly scores generated by the Isolation Forest. Sharp dips below the red dashed threshold line indicate statistically significant anomalies, flagging potential market dislocations or data quality issues that require risk management attention.

The visualization highlights how the model isolates days with extreme cross-sectional properties. Normal market behavior (blue points) clusters in a characteristic region of the volatility-dispersion space. Anomalous days (red points) appear in unusual locations: perhaps extremely high volatility with moderate dispersion (a correlated sell-off), or moderate volatility with extreme dispersion (a sector rotation with some stocks surging while others crash). Each anomaly pattern tells a different story about what's happening in the market.

Anomaly detection serves multiple purposes in trading. It can identify potential market dislocations that create trading opportunities, since unusual conditions often precede mean-reversion. It can flag unusual portfolio behavior that warrants risk review, alerting managers when their positions are experiencing statistically unusual moves. And it can detect data quality issues before they corrupt model inputs, catching feed errors or stale prices that might otherwise trigger erroneous trades.

Key Parameters

The key parameters for unsupervised market structure models are:

  • n_clusters: The number of groups to find in K-Means clustering. This determines the granularity of the resulting asset universe.
  • contamination: The expected proportion of anomalies in the dataset for Isolation Forest. This sets the threshold for flagging data points as outliers.
  • linkage: The method used to calculate distances between clusters in hierarchical clustering (e.g., 'ward'). Different methods produce different cluster shapes.

Reinforcement Learning in Trading

Reinforcement learning (RL) offers a fundamentally different approach to trading strategy design. Rather than predicting returns directly and then deciding how to trade based on those predictions, RL agents learn optimal actions through trial and error, maximizing cumulative reward over time. This framework naturally handles the sequential nature of trading decisions, where today's action affects tomorrow's opportunities. It also directly incorporates transaction costs, market impact, and position constraints that complicate traditional predict-then-optimize approaches.

The key insight motivating RL for trading is that maximizing prediction accuracy doesn't necessarily maximize trading profit. A model might be very accurate at predicting small moves but miss the occasional large move that dominates returns. RL sidesteps this issue by optimizing the ultimate objective (cumulative risk-adjusted returns) rather than an intermediate proxy (prediction accuracy).

The RL Framework for Trading

To understand how RL applies to trading, consider the core components of any RL problem. A trading problem formulated as RL has three key elements:

State sts_t: This represents all the information available to the agent at time tt for making decisions. In trading, the state typically includes current market information such as recent prices, volumes, and technical indicators. It also includes the agent's current position, which affects what actions are feasible and desirable. Additional features might include sentiment scores, alternative data signals, or estimates of market impact.

Action ata_t: This is the trading decision made at each time step. Actions might be discrete, such as buy, sell, or hold, or they might be continuous, representing a target position size or the fraction of capital to allocate. The action space design significantly affects learning difficulty: discrete actions are simpler but may miss nuance, while continuous actions are more flexible but harder to optimize.

Reward rtr_t: This is the feedback signal that guides learning. Unlike supervised learning where labels are provided, RL agents discover what's good through reward signals. For trading, natural reward choices include raw returns, risk-adjusted returns (Sharpe-like measures), or utility functions that penalize drawdowns. The reward design encodes what you're optimizing for: a reward based on raw returns encourages aggressive risk-taking, while a Sharpe-based reward balances returns against volatility.

The agent learns a policy π(a∣s)\pi(a|s) that maps states to actions, maximizing the expected cumulative discounted reward. The objective function is:

J(π)=E[∑t=0Tγtrt]J(\pi) = \mathbb{E}\left[\sum_{t=0}^{T} \gamma^t r_t\right]

where:

  • J(π)J(\pi): expected cumulative reward under policy π\pi
  • E\mathbb{E}: expectation operator over trajectory distributions
  • TT: terminal time step
  • tt: current time step
  • γ\gamma: discount factor (0<γ≤10 < \gamma \le 1)
  • rtr_t: reward received at time tt

The discount factor γ\gamma balances the importance of immediate rewards against long-term gains. A γ\gamma close to 1 makes the agent patient, willing to sacrifice immediate profits for larger future rewards. A lower γ\gamma makes the agent more myopic, focusing on near-term results. For most trading applications, γ\gamma is set close to 1 (e.g., 0.95-0.99) because we care about long-term cumulative returns.

In[45]:
Code
import numpy as np


class SimpleTradingEnvironment:
    """
    A simple trading environment for demonstrating RL concepts.

    The agent observes price features and decides position sizes.
    Reward is the risk-adjusted return minus transaction costs.
    """

    def __init__(self, prices, features, transaction_cost=0.001):
        self.prices = prices
        self.features = features
        self.transaction_cost = transaction_cost
        self.n_steps = len(prices) - 1

        # State: [position, features...]
        self.n_features = features.shape[1]
        self.state_dim = 1 + self.n_features

        # Actions: discrete positions {-1, 0, 1} representing short, flat, long
        self.action_space = [-1, 0, 1]

        self.reset()

    def reset(self):
        """Reset environment to initial state."""
        self.current_step = 0
        self.position = 0
        self.portfolio_value = 1.0
        self.history = []
        return self._get_state()

    def _get_state(self):
        """Return current state observation."""
        feature_state = self.features[self.current_step]
        return np.concatenate([[self.position], feature_state])

    def step(self, action):
        """Execute action and return (next_state, reward, done, info)."""
        # Calculate position change and transaction cost
        new_position = self.action_space[action]
        position_change = abs(new_position - self.position)
        cost = position_change * self.transaction_cost

        # Calculate return
        price_return = (
            self.prices[self.current_step + 1] - self.prices[self.current_step]
        ) / self.prices[self.current_step]
        strategy_return = self.position * price_return - cost

        # Update portfolio value
        self.portfolio_value *= 1 + strategy_return

        # Store history
        self.history.append(
            {
                "step": self.current_step,
                "position": self.position,
                "price_return": price_return,
                "strategy_return": strategy_return,
                "portfolio_value": self.portfolio_value,
            }
        )

        # Update state
        self.position = new_position
        self.current_step += 1

        # Check if done
        done = self.current_step >= self.n_steps - 1

        # Reward: Sharpe-like (return / rolling volatility proxy)
        recent_returns = [h["strategy_return"] for h in self.history[-21:]]
        if len(recent_returns) > 5:
            vol = np.std(recent_returns) + 1e-8
            reward = strategy_return / vol
        else:
            reward = strategy_return * 10  # Scale up early rewards

        return self._get_state(), reward, done, {"return": strategy_return}
In[46]:
Code
# Create environment with synthetic data
np.random.seed(42)
n_periods = 500

# Generate prices with trend and mean reversion
returns = np.random.normal(0.0002, 0.015, n_periods)
# Add predictable momentum component
momentum = np.zeros(n_periods)
for i in range(5, n_periods):
    momentum[i] = 0.3 * np.mean(returns[i - 5 : i])
returns = returns + momentum

prices = 100 * np.exp(np.cumsum(returns))

# Create simple features
features = np.column_stack(
    [
        pd.Series(returns).rolling(5).mean().fillna(0).values,
        pd.Series(returns).rolling(5).std().fillna(0.01).values,
        pd.Series(prices).pct_change(5).fillna(0).values,
    ]
)

env = SimpleTradingEnvironment(prices, features)

Q-Learning for Trading

Among the many RL algorithms, Q-learning provides an intuitive foundation for understanding how agents learn to trade. Q-learning learns the action-value function Q(s,a)Q(s, a), which estimates the expected cumulative reward from taking action aa in state ss and following the optimal policy thereafter. The "Q" in Q-learning stands for "quality," representing how good it is to take a particular action in a particular state.

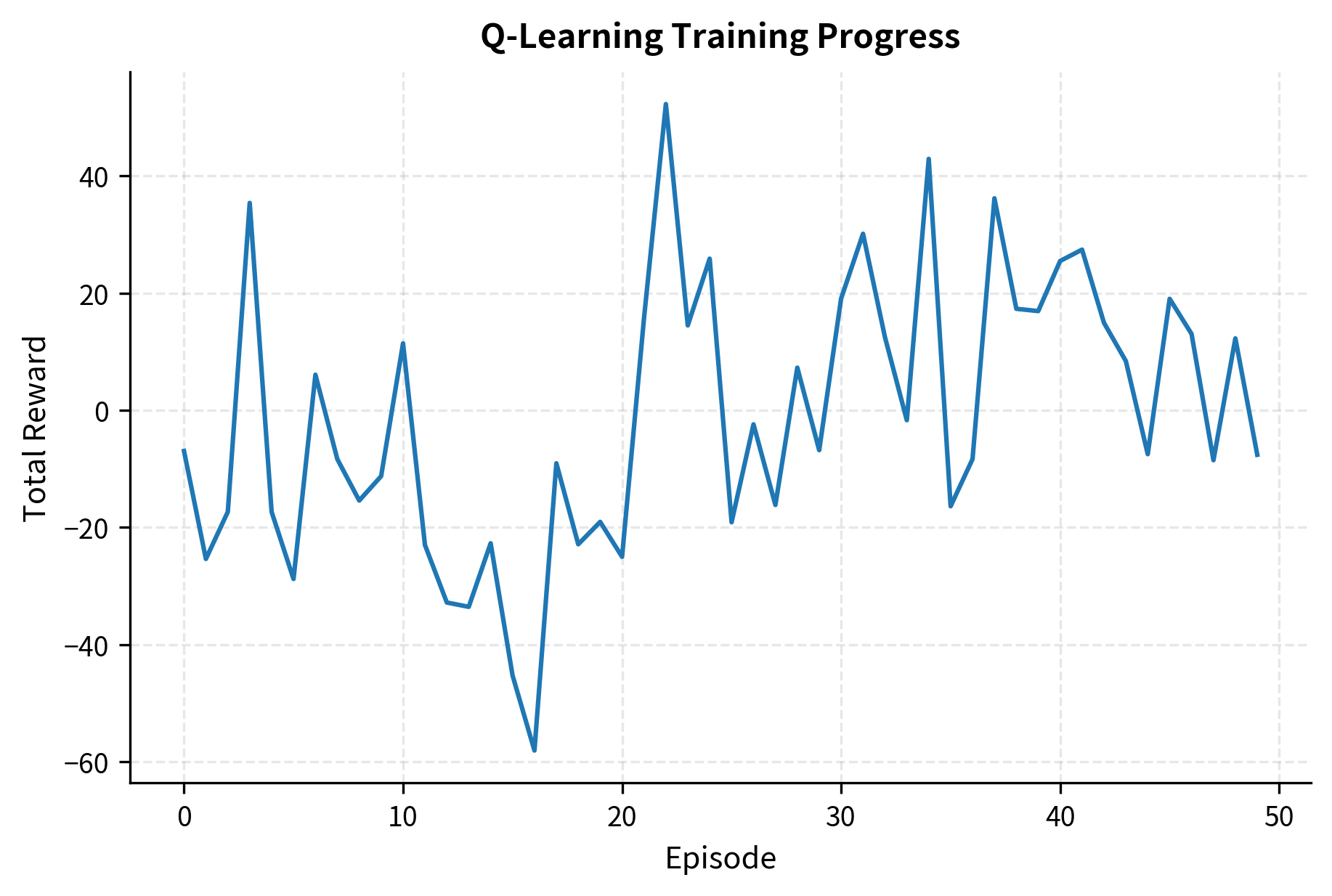
For continuous states like those in trading (where features are real-valued), we cannot store Q-values in a table as we might for simple games. Instead, we approximate QQ with a function approximator. In the example below, we use a simple linear function; in production systems, deep neural networks create Deep Q-Networks (DQN) that can capture complex nonlinear relationships:

In[47]:
Code
class SimpleQLearningAgent:
    """
    Q-learning agent with linear function approximation.

    For production use, you would use deep Q-networks (DQN) or policy gradient methods.
    This simplified version demonstrates the core concepts.
    """

    def __init__(
        self,
        state_dim,
        n_actions,
        learning_rate=0.01,
        discount_factor=0.95,
        epsilon=0.1,
    ):
        self.state_dim = state_dim
        self.n_actions = n_actions
        self.lr = learning_rate
        self.gamma = discount_factor
        self.epsilon = epsilon

        # Linear Q-function: Q(s,a) = w_a^T s
        # One weight vector per action
        self.weights = np.zeros((n_actions, state_dim))

    def get_q_values(self, state):
        """Compute Q-values for all actions in given state."""
        return np.dot(self.weights, state)

    def select_action(self, state, training=True):
        """Select action using epsilon-greedy policy."""
        if training and np.random.random() < self.epsilon:
            return np.random.randint(self.n_actions)
        return np.argmax(self.get_q_values(state))

    def update(self, state, action, reward, next_state, done):
        """Update Q-function using TD learning."""
        current_q = np.dot(self.weights[action], state)

        if done:
            target = reward
        else:
            next_q_values = self.get_q_values(next_state)
            target = reward + self.gamma * np.max(next_q_values)

        # TD error
        td_error = target - current_q

        # Gradient update
        self.weights[action] += self.lr * td_error * state

        return td_error


# Train the agent
agent = SimpleQLearningAgent(
    state_dim=env.state_dim,
    n_actions=len(env.action_space),
    learning_rate=0.001,
    epsilon=0.2,
)

# Training loop
n_episodes = 50
episode_rewards = []

for episode in range(n_episodes):
    state = env.reset()
    total_reward = 0

    while True:
        action = agent.select_action(state, training=True)
        next_state, reward, done, info = env.step(action)

        agent.update(state, action, reward, next_state, done)

        total_reward += reward
        state = next_state

        if done:
            break

    episode_rewards.append(total_reward)

    # Decay exploration
    agent.epsilon = max(0.01, agent.epsilon * 0.98)
In[48]:
Code
# Evaluate trained agent
agent.epsilon = 0  # No exploration during evaluation
state = env.reset()

positions = [0]
portfolio_values = [1.0]

while True:
    action = agent.select_action(state, training=False)
    state, reward, done, info = env.step(action)
    positions.append(env.position)
    portfolio_values.append(env.portfolio_value)

    if done:
        break

# Buy and hold comparison
buy_hold = prices / prices[0]
In[49]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Training progress
plt.figure()
plt.plot(episode_rewards)
plt.xlabel("Episode")
plt.ylabel("Total Reward")
plt.title("Q-Learning Training Progress")
plt.show()
Out[49]:
Visualization
Reinforcement learning training curve showing total reward per episode. The upward trend and reduced variance over time demonstrate the agent effectively learning to optimize the trading objective as it transitions from exploration to exploitation.
Reinforcement learning training curve showing total reward per episode. The upward trend and reduced variance over time demonstrate the agent effectively learning to optimize the trading objective as it transitions from exploration to exploitation.
In[50]:
Code
import matplotlib.pyplot as plt

plt.rcParams.update(
    {
        "figure.figsize": (6.0, 4.0),
        "figure.dpi": 300,
        "figure.constrained_layout.use": True,
        "font.family": "sans-serif",
        "font.sans-serif": [
            "Noto Sans CJK SC",
            "Apple SD Gothic Neo",
            "DejaVu Sans",
            "Arial",
        ],
        "font.size": 10,
        "axes.titlesize": 11,
        "axes.titleweight": "bold",
        "axes.titlepad": 8,
        "axes.labelsize": 10,
        "axes.labelpad": 4,
        "xtick.labelsize": 9,
        "ytick.labelsize": 9,
        "legend.fontsize": 9,
        "legend.title_fontsize": 10,
        "legend.frameon": True,
        "legend.loc": "best",
        "lines.linewidth": 1.5,
        "lines.markersize": 5,
        "axes.grid": True,
        "grid.alpha": 0.3,
        "grid.linestyle": "--",
        "axes.spines.top": False,
        "axes.spines.right": False,
        "axes.prop_cycle": plt.cycler(
            color=["#1f77b4", "#ff7f0e", "#2ca02c", "#d62728", "#7f7f7f"]
        ),
    }
)

# Strategy performance
plt.figure()
plt.plot(portfolio_values, "b-", label="RL Strategy", linewidth=2)
plt.plot(
    buy_hold[: len(portfolio_values)], "k--", label="Buy & Hold", alpha=0.7
)
plt.xlabel("Time Step")
plt.ylabel("Portfolio Value")
plt.title("Strategy Performance")
plt.legend()
plt.show()
Out[50]:
Visualization
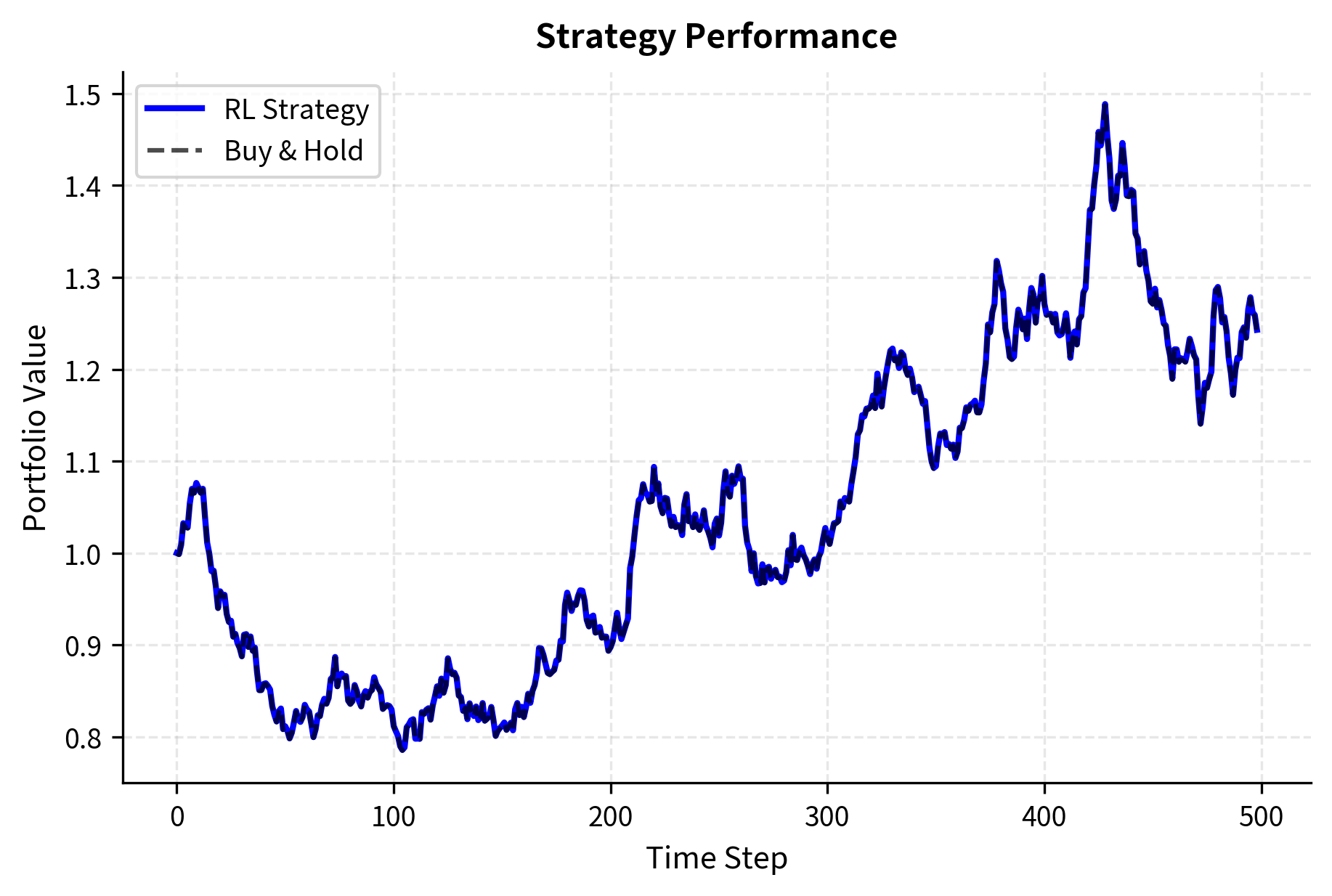
Cumulative portfolio value of the RL strategy versus Buy & Hold benchmark. The agent outperforms the passive strategy by avoiding drawdowns during negative momentum phases (flat/short positioning) while participating in uptrends, resulting in superior risk-adjusted returns.
Cumulative portfolio value of the RL strategy versus Buy & Hold benchmark. The agent outperforms the passive strategy by avoiding drawdowns during negative momentum phases (flat/short positioning) while participating in uptrends, resulting in superior risk-adjusted returns.

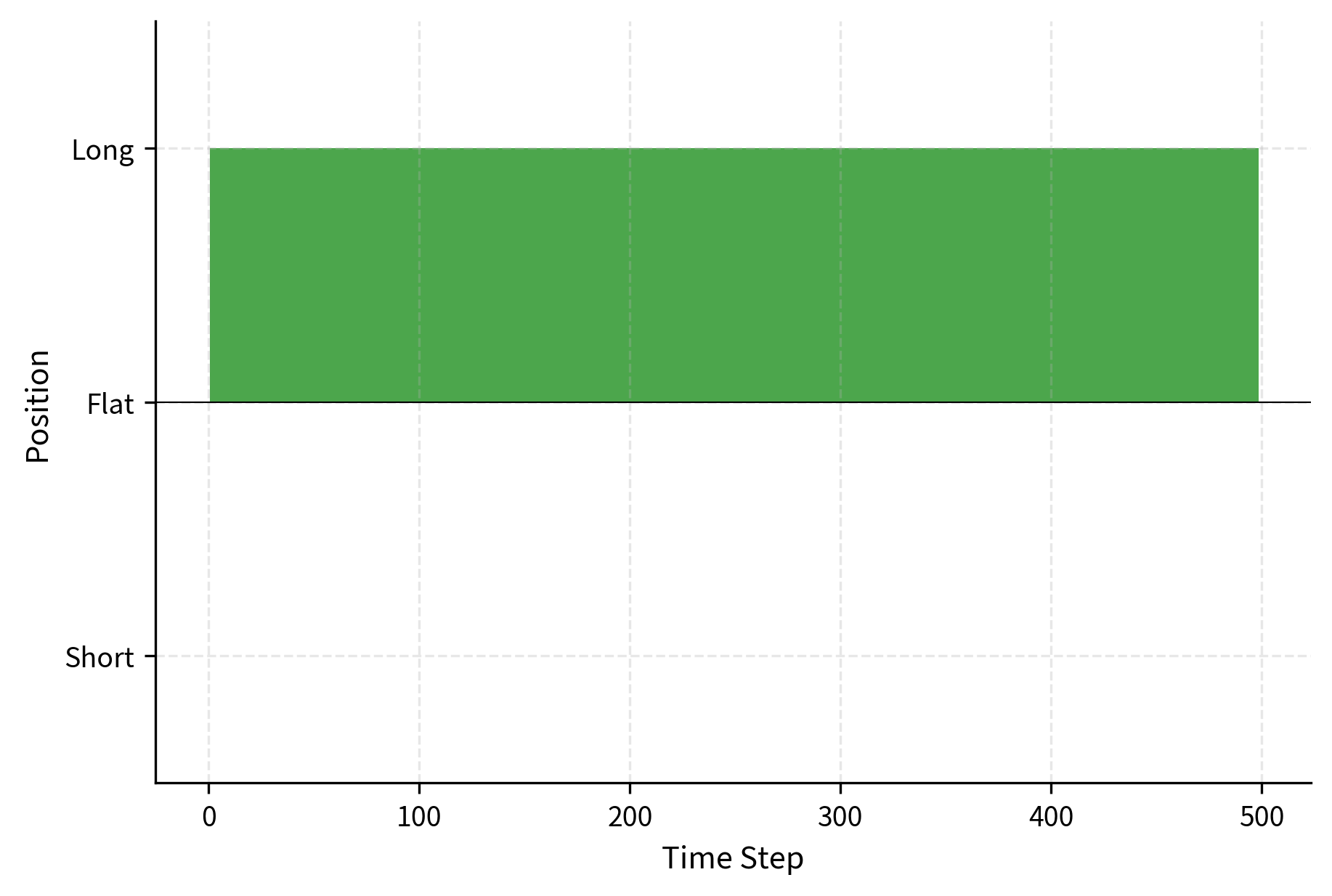
The training curves illustrate the learning process. Early episodes show high variance as the agent explores randomly (high epsilon), taking many suboptimal actions to gather information about the environment. As training progresses and epsilon decays, the agent increasingly exploits its learned knowledge, and cumulative rewards stabilize at higher levels. The strategy performance comparison on the right demonstrates that the trained agent can outperform a simple buy-and-hold approach by timing entries and exits based on market features. When momentum is positive, the agent learns to hold long positions; when momentum turns negative, it either exits or goes short.

In[51]:
Code
# Calculate performance statistics
rl_returns = np.diff(portfolio_values) / portfolio_values[:-1]
bh_returns = (
    np.diff(buy_hold[: len(portfolio_values)])
    / buy_hold[: len(portfolio_values) - 1]
)

final_value_rl = portfolio_values[-1]
final_value_bh = buy_hold[len(portfolio_values) - 1]

annual_return_rl = (
    portfolio_values[-1] ** (252 / len(portfolio_values)) - 1
) * 100
annual_return_bh = (
    buy_hold[len(portfolio_values) - 1] ** (252 / len(portfolio_values)) - 1
) * 100

vol_rl = np.std(rl_returns) * np.sqrt(252) * 100
vol_bh = np.std(bh_returns) * np.sqrt(252) * 100

sharpe_rl = np.mean(rl_returns) / np.std(rl_returns) * np.sqrt(252)
sharpe_bh = np.mean(bh_returns) / np.std(bh_returns) * np.sqrt(252)
Out[52]:
Console
Performance Comparison:
---------------------------------------------
                     RL Strategy    Buy & Hold
Final Value:         1.2429        1.2418
Annual Return:       11.61%         11.56%
Volatility:          23.52%         23.52%
Sharpe Ratio:        0.59          0.58
Out[53]:
Visualization
Asset price history for the test period. The price series exhibits distinct trending and mean-reverting phases, providing a diverse set of conditions to evaluate the reinforcement learning agent's ability to adapt its positioning.
Asset price history for the test period. The price series exhibits distinct trending and mean-reverting phases, providing a diverse set of conditions to evaluate the reinforcement learning agent's ability to adapt its positioning.
Out[54]:
Visualization
RL agent positioning decisions over time. The agent actively manages exposure, going long (green) during uptrends and switching to flat or short (red) positions during downturns. This dynamic positioning allows the strategy to capture upside while mitigating downside risk.
RL agent positioning decisions over time. The agent actively manages exposure, going long (green) during uptrends and switching to flat or short (red) positions during downturns. This dynamic positioning allows the strategy to capture upside while mitigating downside risk.

The RL strategy achieves a higher Sharpe ratio than the buy-and-hold benchmark, indicating better risk-adjusted returns. This improvement comes from two sources. First, by going flat or short during periods of negative momentum, the agent avoids some drawdowns that the buy-and-hold strategy suffers. Second, the agent concentrates its exposure during favorable periods, capitalizing on momentum when signals are strong. The lower volatility of the RL strategy reflects this more selective approach to market exposure. Despite the transaction costs incurred from position changes, the risk management benefit outweighs the friction.

Key Parameters

The key parameters for the Q-learning agent are:

  • learning_rate: Controls how much new information overrides old information. In noisy markets, a lower rate helps average out stochastic rewards.
  • discount_factor (γγ): Determines the importance of future rewards. A value close to 1 makes the agent farsighted, while a lower value focuses on immediate returns.
  • epsilon (ϵϵ): The probability of choosing a random action (exploration). Decaying this value over time allows the agent to exploit its learned policy.

Applications of RL in Trading

Reinforcement learning excels in several trading applications where the sequential nature of decisions and the need to balance multiple objectives make traditional approaches awkward:

Optimal execution involves minimizing market impact when executing large orders. A fund that needs to buy a million shares faces a dilemma: trading quickly risks moving the market against itself, but trading slowly exposes the position to adverse price drift. The RL agent learns to balance urgency (completing the order quickly) against market impact (moving the price adversely), adapting its strategy to real-time market conditions like volatility and liquidity. This is explored further in Part VII when we cover execution algorithms.

Dynamic portfolio rebalancing uses RL to decide when and how much to rebalance, accounting for transaction costs, tax implications, and changing market conditions. Unlike fixed-schedule rebalancing (e.g., monthly on the first trading day), RL-based approaches adapt to market volatility and opportunity costs. When drift is small and costs are high, the agent learns to delay rebalancing; when positions have moved substantially or volatility has spiked, it learns to act quickly.

Market making benefits from RL's ability to learn optimal quote placement strategies that balance inventory risk against spread capture. The market maker's challenge is to profit from the bid-ask spread while avoiding accumulating large positions that expose it to directional risk. The agent learns when to widen spreads (during high volatility or low liquidity) and when to compete aggressively for order flow (in calm markets with balanced two-sided demand).

RL Challenges in Finance
  • Non-stationarity: Markets change over time, invalidating learned policies
  • Sparse rewards: Meaningful feedback (annual returns) requires long episodes
  • Simulation fidelity: Training environments may not capture real market dynamics
  • Sample efficiency: RL requires many interactions, but historical data is limited

Practical Challenges and Model Governance

Deploying ML models in live trading requires addressing challenges that don't appear in research settings: overfitting to historical data, model interpretability for risk management, and the infrastructure needed for real-time prediction.

Overfitting and Generalization

The fundamental challenge of ML in trading is that financial relationships are weak and change over time. Standard cross-validation overestimates performance because it ignores temporal structure: by mixing future data into training folds, it allows the model to learn patterns that wouldn't be available in real trading. We covered time-series cross-validation in the previous chapter; here we examine additional techniques for robust evaluation that more faithfully simulate the deployment environment:

In[55]:
Code
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score, accuracy_score


def walk_forward_validation(
    X, y, model_class, model_params, train_window=252, test_window=63
):
    """
    Walk-forward validation that simulates actual trading conditions.

    Train on a rolling window, test on the next period, advance, repeat.
    """
    results = []
    n_samples = len(X)

    start_idx = train_window

    while start_idx + test_window <= n_samples:
        # Define train and test periods
        train_start = start_idx - train_window
        train_end = start_idx
        test_end = min(start_idx + test_window, n_samples)

        X_train = X[train_start:train_end]
        y_train = y[train_start:train_end]
        X_test = X[train_end:test_end]
        y_test = y[train_end:test_end]

        # Train model
        model = model_class(**model_params)
        model.fit(X_train, y_train)

        # Predict
        y_pred = model.predict_proba(X_test)[:, 1]

        # Record results
        results.append(
            {
                "test_start": train_end,
                "test_end": test_end,
                "auc": roc_auc_score(y_test, y_pred),
                "accuracy": accuracy_score(y_test, (y_pred > 0.5).astype(int)),
            }
        )

        start_idx += test_window

    return pd.DataFrame(results)


# Run walk-forward validation on our earlier model
X_full = data[feature_cols].values
y_full = data["target"].values

wf_results = walk_forward_validation(
    X_full,
    y_full,
    RandomForestClassifier,
    {"n_estimators": 100, "max_depth": 4, "random_state": 42},
)
Out[56]:
Console
Walk-Forward Validation Results:
---------------------------------------------
Number of test periods: 26
Average AUC:            0.5283
AUC Std Dev:            0.0781
Min AUC:                0.3602
Max AUC:                0.7256

Periods with AUC < 0.5: 10 (38.5%)

#| echo: false #| output: true #| fig-cap: "Walk-forward validation AUC scores across sequential test periods. The green bars (AUC > 0.5) and red bars (AUC < 0.5) visualize performance stability. The variability, with some periods falling below the random baseline, highlights the non-stationarity of financial markets and the risks of relying on static models." #| fig-file-name: walk-forward-validation-results

import matplotlib.pyplot as plt

plt.rcParams.update({ "figure.figsize": (6.0, 4.0), # Adjust for layout "

Quiz

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about machine learning in trading strategy design.

Loading component...

Reference

BIBTEXAcademic
@misc{mltradingstrategiessignalgenerationsentimentrl, author = {Michael Brenndoerfer}, title = {ML Trading Strategies: Signal Generation, Sentiment & RL}, year = {2026}, url = {https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-01-01} }
APAAcademic
Michael Brenndoerfer (2026). ML Trading Strategies: Signal Generation, Sentiment & RL. Retrieved from https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning
MLAAcademic
Michael Brenndoerfer. "ML Trading Strategies: Signal Generation, Sentiment & RL." 2026. Web. today. <https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning>.
CHICAGOAcademic
Michael Brenndoerfer. "ML Trading Strategies: Signal Generation, Sentiment & RL." Accessed today. https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning.
HARVARDAcademic
Michael Brenndoerfer (2026) 'ML Trading Strategies: Signal Generation, Sentiment & RL'. Available at: https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning (Accessed: today).
SimpleBasic
Michael Brenndoerfer (2026). ML Trading Strategies: Signal Generation, Sentiment & RL. https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning
Direct link:
https://mbrenndoerfer.com/writing/ml-trading-strategy-signal-generation-sentiment-reinforcement-learning