Unigram Language Model Tokenization: Probabilistic Subword Segmentation

Unigram Language Model TokenizationLink Copied

IntroductionLink Copied

Subword tokenization methods like Byte Pair Encoding (BPE) work by greedily merging the most frequent character pairs. But what if we could make smarter decisions about which merges to perform? The Unigram Language Model approach treats tokenization as a probabilistic optimization problem, asking: "What's the most likely way to segment this text into tokens?"

At its core, unigram LM tokenization trains a language model on subword units and uses it to find the tokenization that maximizes the probability of the text. This approach, popularized by the SentencePiece library, offers several advantages over deterministic methods like BPE.

Rather than applying fixed merge rules, unigram tokenization learns a vocabulary of subword units where each unit has an associated probability. During tokenization, the algorithm searches for the segmentation that gives the highest total probability under this model.

Technical Deep DiveLink Copied

Unigram Language Model FormulationLink Copied

A unigram language model assigns probabilities to individual tokens independently. For tokenization, we want to segment text into a sequence of subword tokens that maximizes the joint probability:

where:

• $n$: number of tokens in the segmentation
• $\text{token}_i$: the $i$-th subword token in the sequence
• $V$: the learned vocabulary of subword units

We can represent any word as a sequence of subword tokens from $V$. For example, the word "tokenization" might be segmented as ["token", "ization"] or ["tok", "en", "ization"], and we want to choose the segmentation with the highest probability.

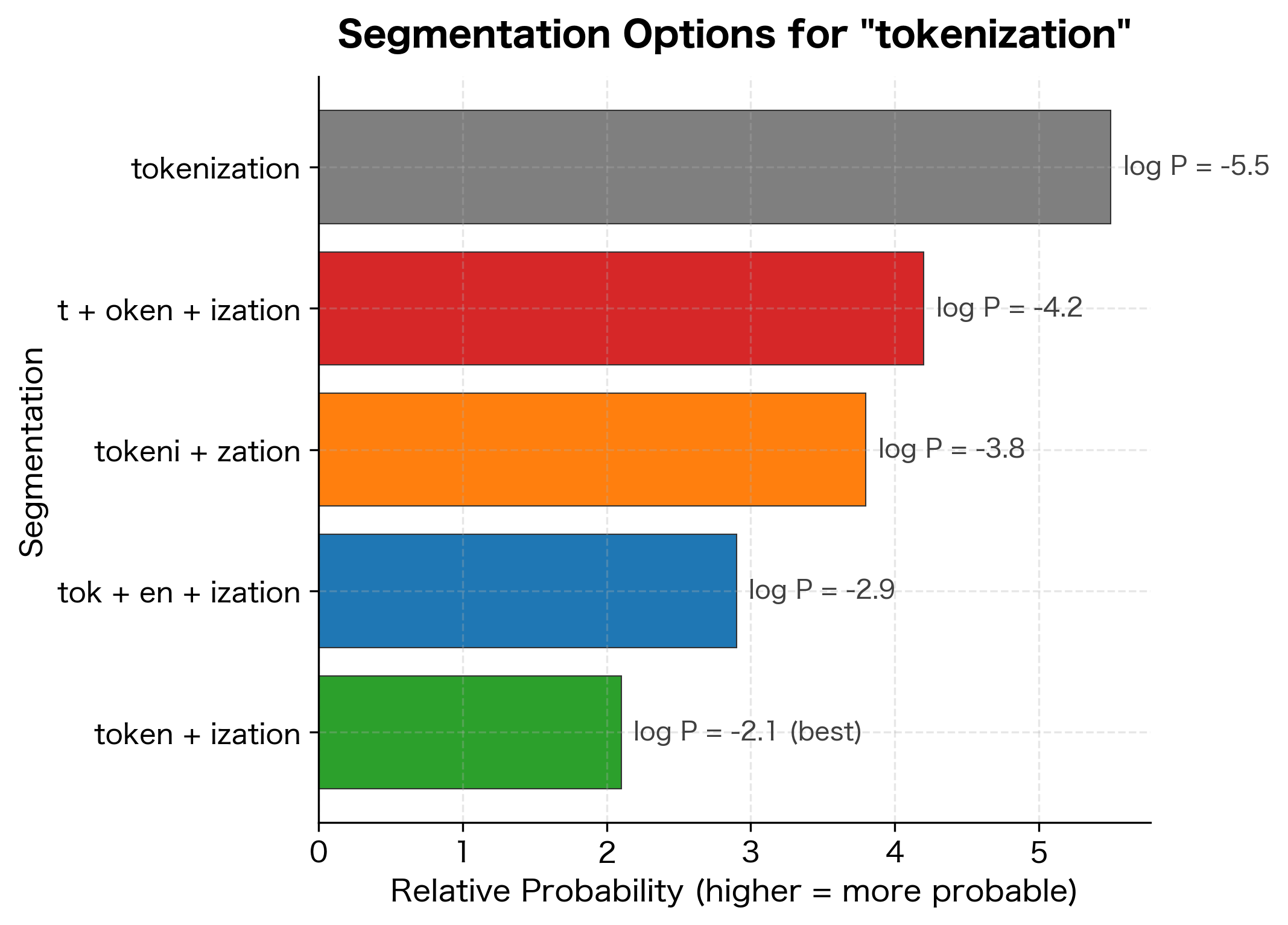
To illustrate this concept, let's visualize different possible segmentations of the word "tokenization" with their associated probabilities. The unigram model learns that certain subword units like "token" and "ization" are more probable than arbitrary splits.

This visualization shows how the unigram model evaluates different ways to split a word. The most probable segmentation combines meaningful subword units ("token" + "ization") that frequently appear in the training corpus. Less natural splits receive lower probabilities, guiding the model toward linguistically sensible token boundaries.

The EM Algorithm for TrainingLink Copied

Training a unigram language model for tokenization uses an Expectation-Maximization (EM) algorithm, adapted specifically for the tokenization task. Unlike standard language model training, the EM algorithm here must consider all possible ways to segment each word in the corpus. We start with a large initial vocabulary (typically all possible substrings up to a maximum length) and iteratively refine both the vocabulary and the token probabilities.

E-Step: Compute Tokenization Probabilities

For each word in our training corpus, we compute the probability of all possible ways to segment it using the current vocabulary. This gives us the expected count of each subword token across all possible segmentations.

M-Step: Update Probabilities

We update the probability of each token proportional to its expected count:

where:

• $\text{expected\_count}(\text{token})$: expected frequency of the token across all possible segmentations of the training corpus
• $V$: current vocabulary of subword units

The algorithm also includes a vocabulary pruning step that removes low-probability tokens to keep the vocabulary size manageable.

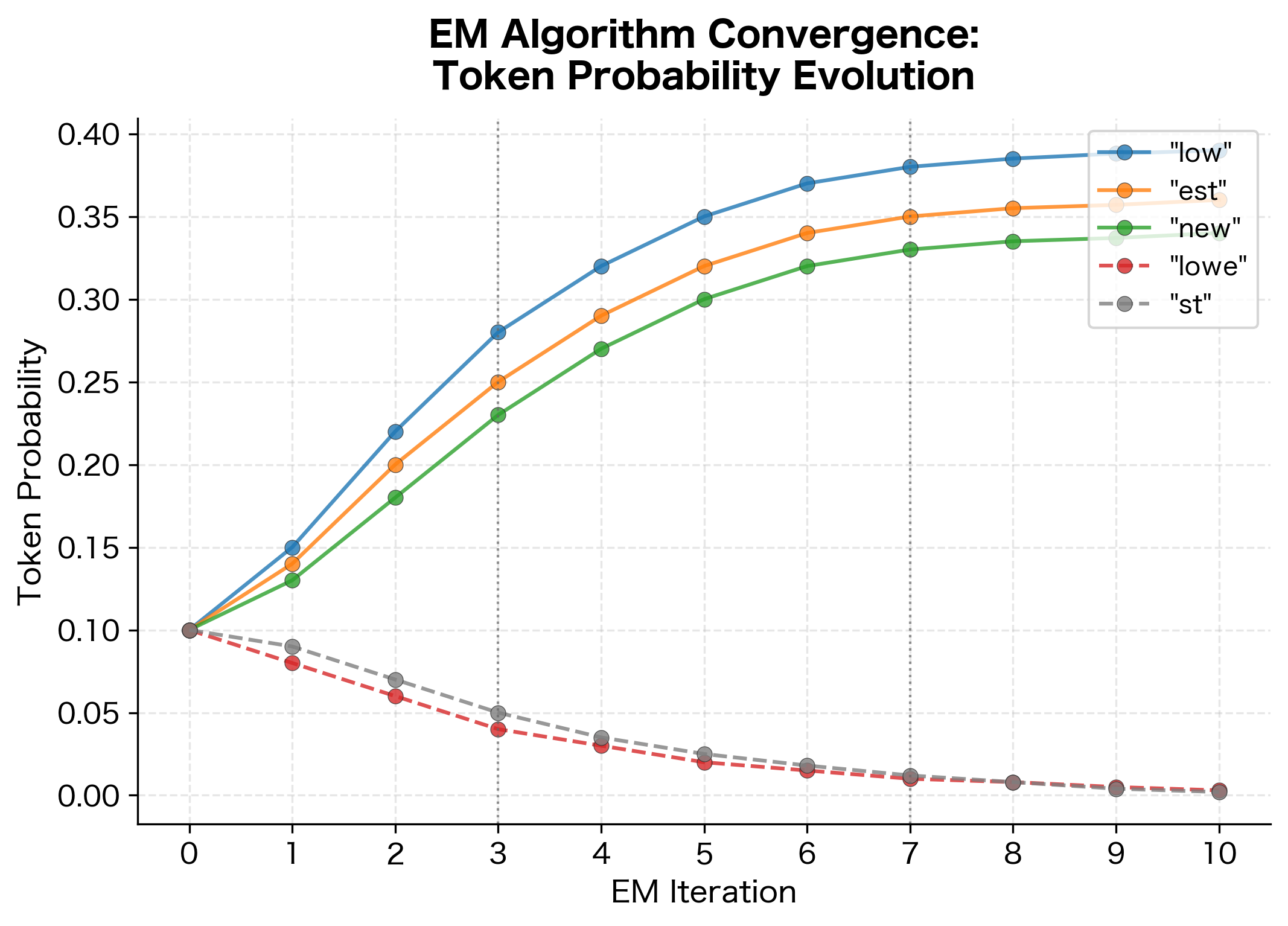
To illustrate the EM algorithm's learning process, let's visualize how token probabilities evolve over iterations. The algorithm starts with uniform probabilities and gradually learns which subword units are more frequent in the corpus.

This visualization demonstrates the EM algorithm's learning dynamics. Initially, all tokens have equal probability. Over iterations, meaningful subword units that frequently appear in the corpus ("low", "est", "new") gain probability, while less useful or nonexistent tokens are gradually pruned away. The algorithm converges when the token probabilities stabilize, resulting in a vocabulary optimized for the corpus's subword patterns.

Viterbi Decoding for TokenizationLink Copied

Once we have our trained unigram model, tokenization becomes a search problem: find the segmentation of the input text that gives the highest probability. This is solved using the Viterbi algorithm, a dynamic programming approach for finding the most likely sequence.

For a word $w$ of length $L$, we want to find positions $0 = p_0 < p_1 < \dots < p_k = L$ that define the token boundaries, maximizing:

where:

• $w$: input word to tokenize
• $L$: length of the word in characters
• $p_0, p_1, \dots, p_k$: token boundary positions (with $p_0 = 0$ and $p_k = L$)
• $w[p_{i-1}:p_i]$: substring of $w$ from position $p_{i-1}$ to $p_i$
• $k$: number of tokens in the segmentation

The Viterbi algorithm efficiently finds the most probable segmentation by using dynamic programming to track the best probability path to each position in the word, avoiding the need to enumerate all possible segmentations.

Sampling Multiple SegmentationsLink Copied

While Viterbi gives us the single best segmentation, we might want to sample from the distribution of possible segmentations. This is useful for data augmentation and creating more robust models.

The sampling algorithm works by:

1. Computing all possible token boundaries at each position
2. Sampling tokens according to their probabilities
3. Building a complete segmentation by sampling sequentially

This approach can generate multiple valid tokenizations for the same text, which helps models learn more robust representations.

Subword RegularizationLink Copied

Subword regularization is a technique that randomly samples different tokenizations during training. Instead of always using the same segmentation, we sometimes use alternative segmentations that have lower but still reasonable probabilities.

This regularization helps models become more robust to different tokenization choices and improves generalization, especially for morphologically rich languages.

A Worked ExampleLink Copied

Let's work through a detailed example to understand how unigram tokenization processes text. This will show how the algorithm learns from data and makes tokenization decisions.

Suppose we have a small training corpus:

This corpus contains morphological patterns we want the model to learn: "low" appears in "low", "lower", and "lowest"; "est" appears in "lowest" and "newest"; "new" appears in "new" and "newest".

Step 1: Initial Vocabulary ConstructionLink Copied

We start with all possible substrings up to a maximum length (typically 4-6 characters for efficiency). For our corpus, this includes:

Character-level tokens: "l", "o", "w", "e", "s", "t", "n", "r" Bigram tokens: "lo", "ow", "we", "es", "st", "ne", "ew", "er" Trigram tokens: "low", "owe", "wer", "est", "new", "wes" Longer tokens: "lower", "lowest", "newest"

Step 2: EM Training ProcessLink Copied

The EM algorithm iteratively refines token probabilities:

E-Step: For each word, compute the probability of all possible segmentations using current token probabilities. For "lowest":

• ["low", "est"]: P(low) × P(est) = high probability
• ["lowe", "st"]: P(lowe) × P(st) = medium probability
• ["l", "o", "w", "e", "s", "t"]: product of 6 character probabilities = low probability

M-Step: Update token probabilities based on expected frequencies across all segmentations in the corpus.

After several iterations, tokens that appear frequently get higher probabilities:

• "low": appears in "low", "lower", "lowest" → high probability
• "est": appears in "lowest", "newest" → high probability
• "new": appears in "new", "newest" → high probability
• Rare tokens like "lowest" (appears only once) → lower probability

Step 3: Tokenization of New TextLink Copied

When tokenizing "lowest" using the trained model, the Viterbi algorithm evaluates possible segmentations:

The algorithm chooses ["low", "est"] because it maximizes the joint probability while using the fewest, most meaningful tokens.

This example demonstrates the core principles: unigram tokenization learns which subword units are most probable from the training data, then uses dynamic programming to find optimal segmentations. The probabilistic approach allows for more linguistically sensible token boundaries compared to rule-based methods.

Code ImplementationLink Copied

Now let's see these concepts in action using SentencePiece, a practical implementation of unigram tokenization. The following code demonstrates the complete pipeline from corpus preparation to tokenization.

Let's implement unigram tokenization using SentencePiece, which provides an efficient implementation of the unigram model.

The vocabulary shows our learned subword units, with more frequent patterns like "low" and "est" having higher probabilities (less negative log probabilities).

The tokenization results show how our trained unigram model segments different words. For "lowest" and "newest", the model correctly identifies "low"/"new" and "est" as meaningful subword units that appear frequently in the training corpus. The "unknownword" gets segmented into individual characters because it contains no familiar patterns, demonstrating how the model falls back to character-level tokenization for out-of-vocabulary inputs.

The sampling demonstration shows different possible ways to segment "lowest". The first sample represents the most probable segmentation found by Viterbi decoding, while the others show alternative segmentations that could be sampled during training for regularization. Note that SentencePiece's built-in sampling support is limited, so custom sampling implementations are often used for advanced subword regularization techniques.

Key ParametersLink Copied

vocab_size: Controls the final vocabulary size after training. Larger vocabularies can capture more subword patterns but increase memory usage. Typical values range from 8K-32K for modern models.

model_type='unigram': Specifies the unigram language model approach. SentencePiece also supports BPE mode for comparison.

character_coverage: Determines what fraction of characters to include (1.0 = all characters). Important for multilingual text to ensure all scripts are covered.

unk_piece: The token used for unknown characters/subwords. Essential for handling out-of-vocabulary text gracefully.

To illustrate the difference between Unigram LM and BPE tokenization, let's compare how they segment the same text. Unigram LM makes probabilistic decisions based on learned token frequencies, while BPE follows deterministic merge rules.

This comparison highlights key differences between the approaches. Unigram LM assigns probabilities to each token based on corpus statistics, enabling more nuanced decisions. BPE follows deterministic rules but may create less linguistically meaningful segments. The probabilistic nature of Unigram LM allows for better handling of morphological variations and out-of-vocabulary words.

Limitations & ImpactLink Copied

Unigram tokenization offers probabilistic segmentation but comes with trade-offs. The EM training can be computationally expensive for large vocabularies, though SentencePiece optimizes this well. The independence assumption ignores token co-occurrence patterns that could inform better segmentation.

SentencePiece's unigram mode powers tokenization in models like T5, mBART, and many multilingual systems. By learning from actual text rather than applying heuristic rules, unigram tokenization handles diverse languages and domains more robustly than BPE.

The probabilistic approach also enables advanced features like subword regularization, which has improved the robustness of large language models. While BPE remains popular for its simplicity, unigram tokenization offers a more principled approach to the tokenization problem.

SummaryLink Copied

Unigram language model tokenization represents a significant advancement in subword tokenization by treating segmentation as a probabilistic optimization problem. Instead of applying fixed merge rules like BPE, this approach learns a probability distribution over subword units and uses dynamic programming to find the most likely segmentation.

The method combines several sophisticated techniques: an EM algorithm adapted for tokenization that considers all possible word segmentations, Viterbi decoding for efficient segmentation finding, and optional subword regularization for improved robustness. While more computationally intensive than deterministic approaches, unigram tokenization provides superior handling of morphological variation, out-of-vocabulary words, and multilingual text.

This probabilistic framework underlies many modern tokenization systems and demonstrates how statistical learning can produce more linguistically informed text segmentation than rule-based methods.

QuizLink Copied

Ready to test your understanding of unigram language model tokenization? This quiz covers the probabilistic approach to subword segmentation, EM training, and practical implementation.