Master word analogy evaluation using 3CosAdd and 3CosMul methods. Learn the parallelogram model, evaluation datasets, and what analogies reveal about embedding quality.

This article is part of the free-to-read Language AI Handbook
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Word Analogy
Something remarkable happens when you train Skip-gram or CBOW on billions of words: the resulting embeddings exhibit structured geometric relationships that mirror semantic relationships. The famous example: . This isn't a quirk. The vector from "man" to "woman" captures a gender relationship, and adding it to "king" lands near "queen." The embedding space has learned that kingship relates to queenship the same way manhood relates to womanhood.
This phenomenon, known as word analogy, became a central way to evaluate and understand word embeddings. If an embedding space correctly solves "man is to woman as king is to ?", it suggests the model has captured meaningful semantic structure. But analogies also reveal limitations: they work well for certain relationship types and fail for others, and the popular evaluation metrics can be misleading.
This chapter explores the parallelogram model underlying word analogies, develops the mathematical methods for solving them (3CosAdd and 3CosMul), examines standard evaluation datasets, and discusses what analogies actually tell us about embedding quality.
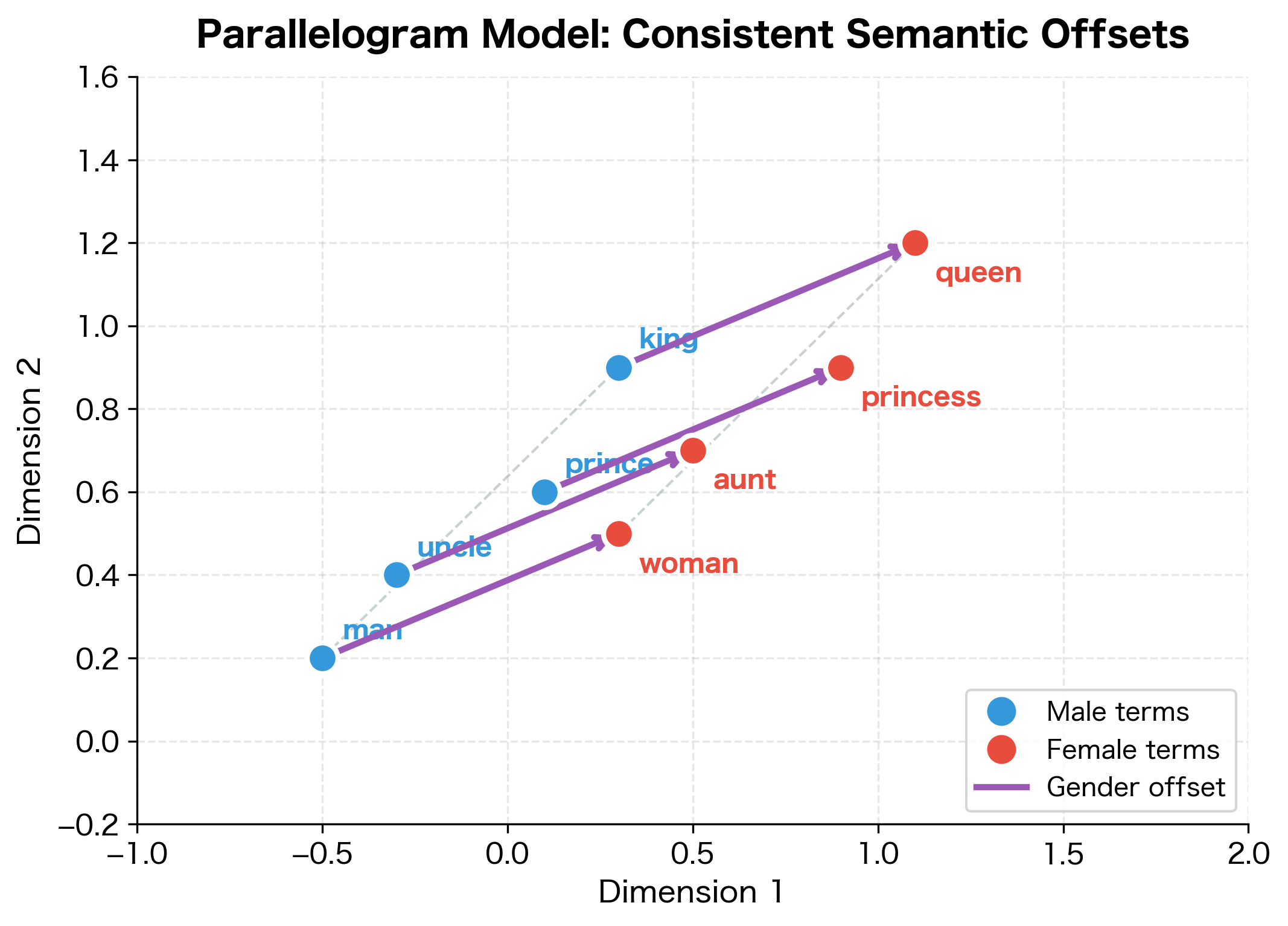
The Parallelogram Model
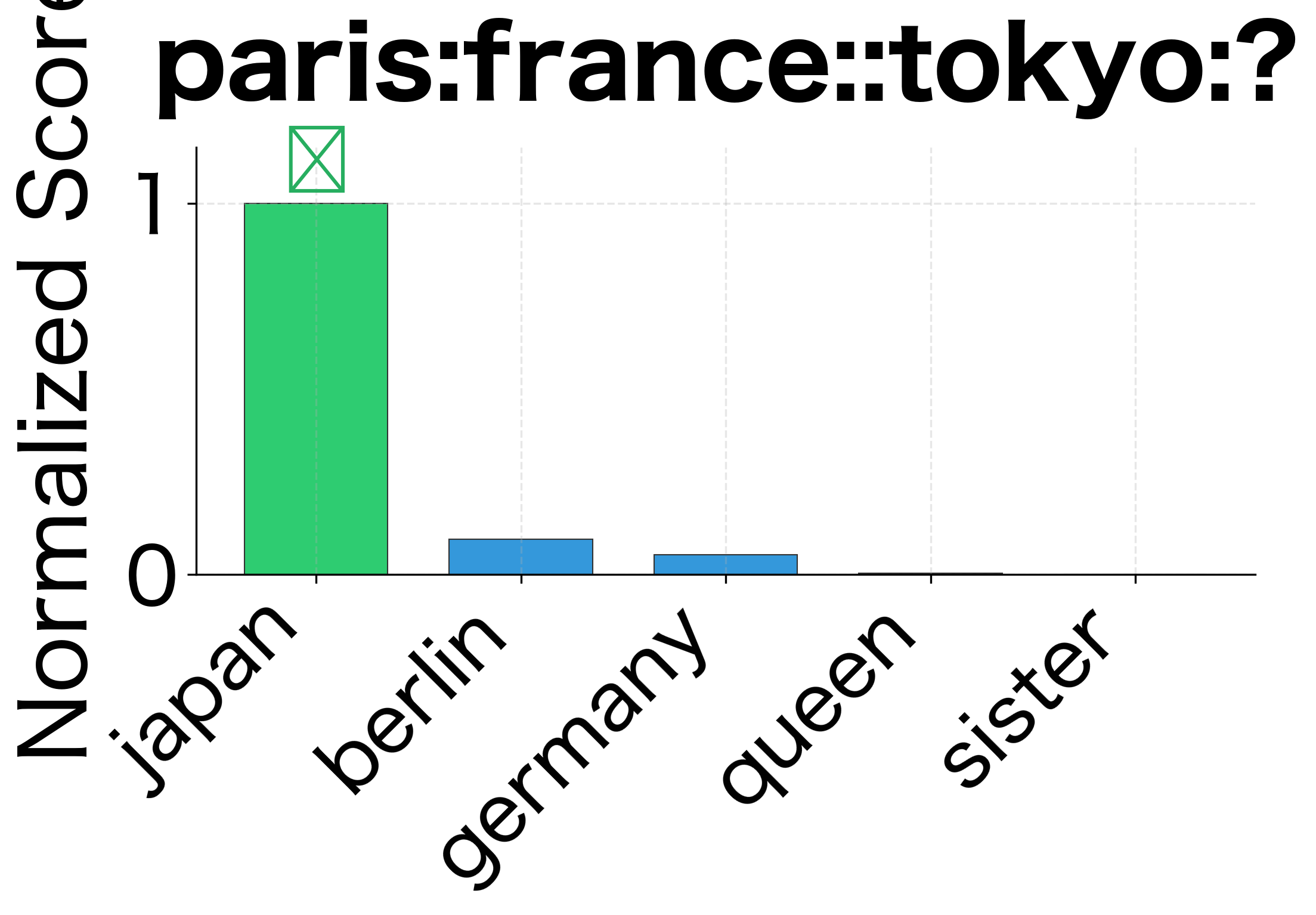
Word analogies rely on a geometric intuition: if two word pairs share the same relationship, the vectors connecting them should be parallel. Consider the relationship "capital of":
- Paris is the capital of France
- Tokyo is the capital of Japan
- London is the capital of England
If embeddings capture this relationship consistently, then , , and should all point in roughly the same direction. This directional consistency allows us to complete analogies.
The parallelogram model assumes that semantic relationships are encoded as consistent vector offsets. If words and share a relationship (e.g., "man" and "woman" share a gender relationship), and words and share the same relationship (e.g., "king" and "queen"), then the offset vectors should be approximately equal: . Geometrically, this means the four word vectors form a parallelogram in embedding space, where the two relationship vectors are parallel sides.
The parallelogram structure is idealized. Real embeddings have noise, and the offsets aren't perfectly parallel. But when embeddings are trained well, the relationship vectors are similar enough that analogy completion works.
Vector Arithmetic for Analogies
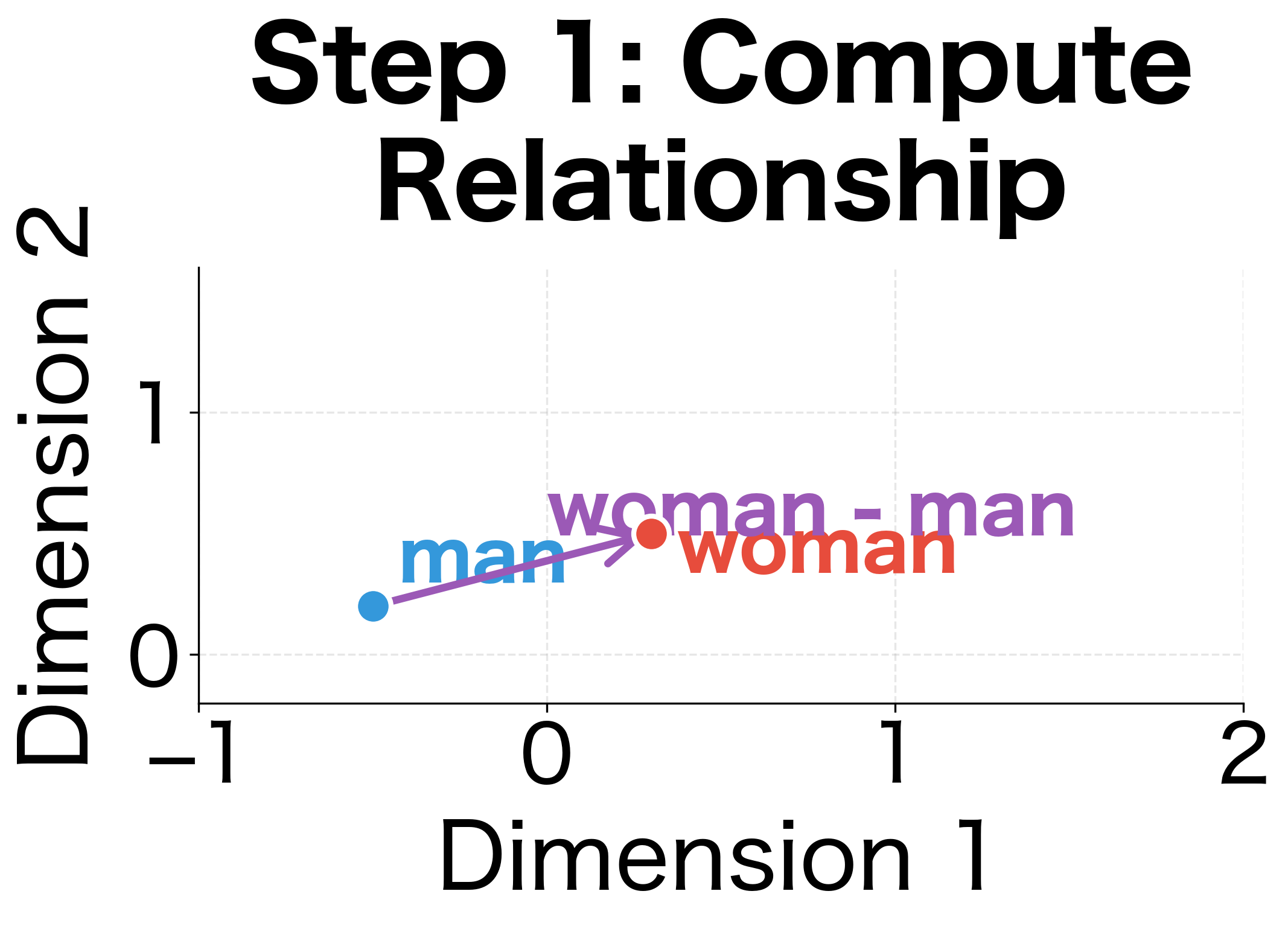
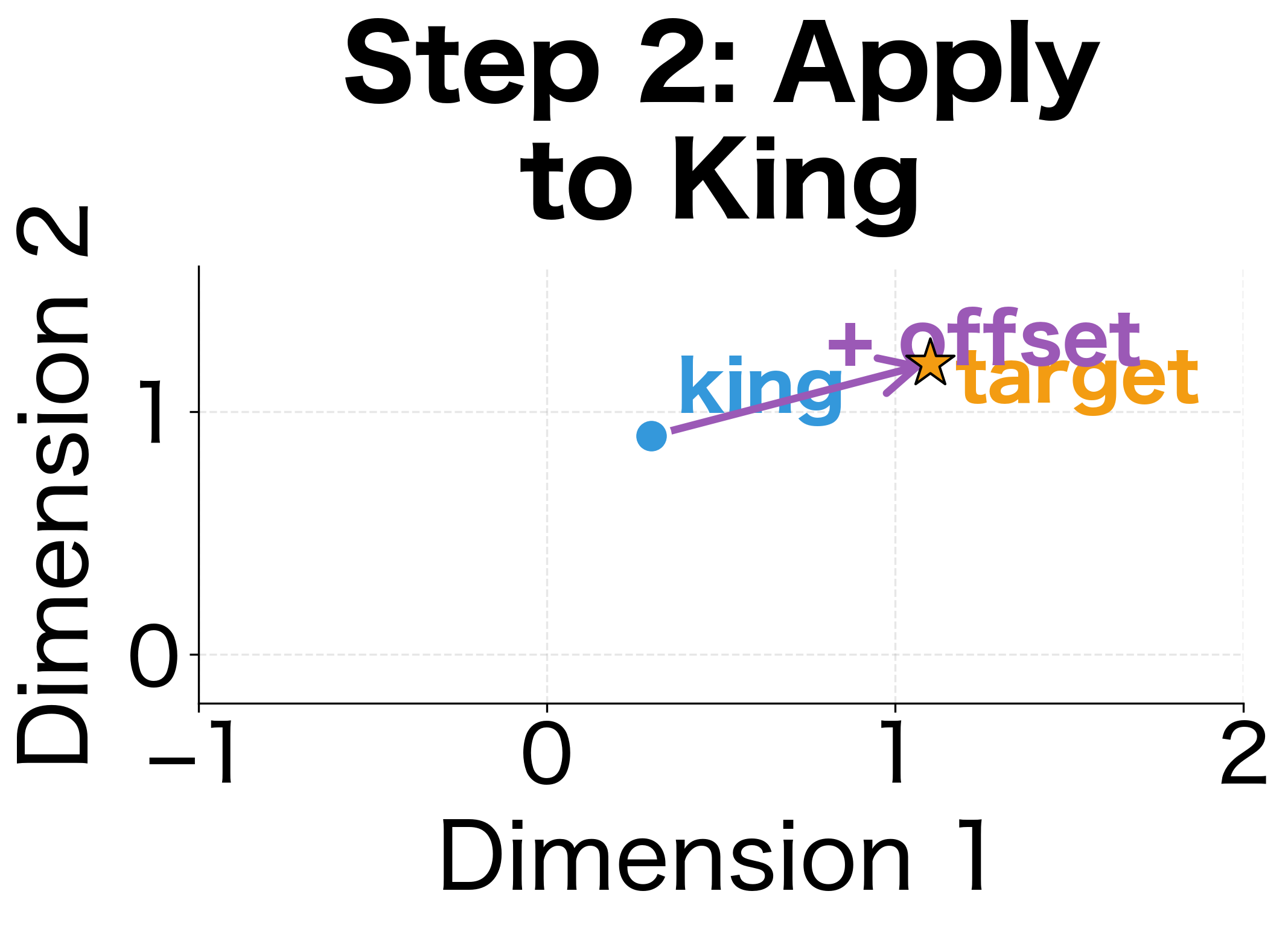
The classic analogy task asks: "a is to b as c is to ?" We need to find a word that completes the analogy. The key insight is that if the relationship between and is the same as the relationship between and , then the vector offsets should be equal. Rearranging this gives us the target vector:
where:
- , , , : embedding vectors for words , , , and
- : the relationship vector capturing how differs from
- : the starting point for our new word pair
The intuition behind this formula:
- Compute the relationship vector: captures how differs from
- Apply this offset to : adding to should land near
- Find the nearest word: search the vocabulary for the word closest to the computed vector
The distance of zero confirms that our synthetic embeddings exhibit perfect parallelogram structure: the computed target vector exactly matches the embedding for "queen." In real embeddings, there's noise, so we need to find the nearest vocabulary word.
The 3CosAdd Method
We've established the intuition: semantic relationships create parallel vectors, and we can complete analogies by adding relationship offsets. But how do we actually find the answer word? In our 2D visualization, we could simply look at where the target vector lands. In 50 or 300 dimensions, we need a principled search procedure.
The challenge is that the target vector almost never exactly equals any word's embedding. Real embeddings have noise, relationships aren't perfectly parallel, and we're working in high-dimensional spaces where geometric intuitions can mislead. What we need is a way to find the closest word to our computed target.
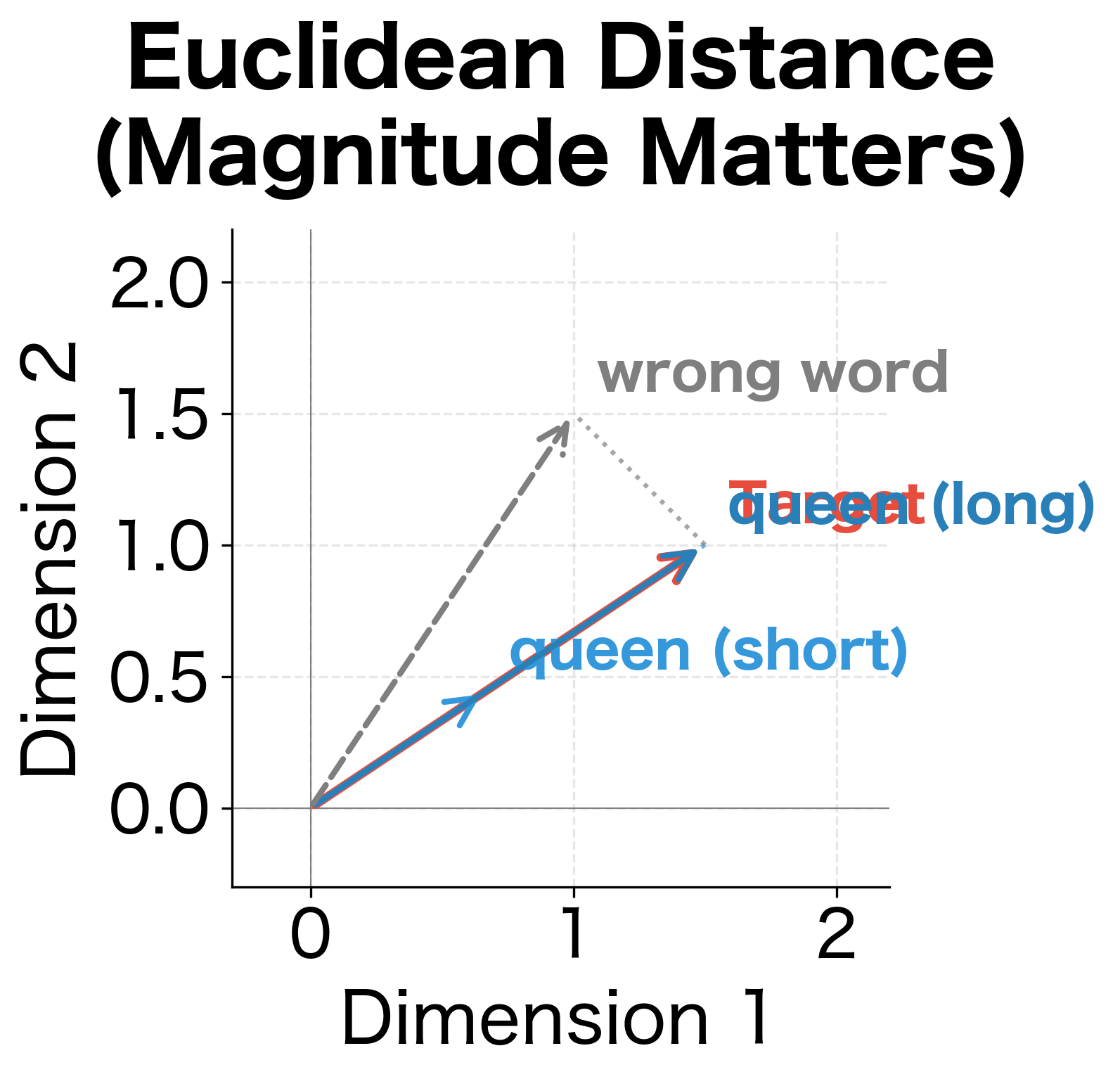
Why Cosine Similarity, Not Euclidean Distance?
You might think: just find the word with minimum Euclidean distance to the target vector. But consider what happens when embeddings have different magnitudes. A frequent word like "the" might have a large embedding norm, while a rare word like "czar" has a small norm. Euclidean distance would favor words whose norms happen to match the target, regardless of directional similarity.
Cosine similarity solves this by focusing purely on direction. It measures the cosine of the angle between two vectors:
where:
- , : the two vectors being compared
- : the dot product of the vectors (sum of element-wise products)
- , : the Euclidean norms (lengths) of the vectors
The denominator normalizes the dot product by the vector lengths, making the result independent of magnitude. Two vectors pointing in the same direction have cosine similarity 1, regardless of their lengths. Perpendicular vectors have similarity 0. Opposite directions yield -1. For analogy completion, we care about direction (does this word's embedding point the same way as our target?), not magnitude.
The 3CosAdd Formula
Given the analogy "a is to b as c is to ?", the 3CosAdd method searches the entire vocabulary to find the word whose embedding is most similar (by cosine) to our target vector. The method gets its name from combining three terms additively: we add and while subtracting :
where:
- : the optimal answer word (the word that maximizes the score)
- : returns the word that achieves the maximum value
- : vocabulary (the set of all words with embeddings)
- : vocabulary excluding the query words
- , , : the query words in the analogy " is to as is to ?"
- : embedding vector for candidate word
- : the target vector computed by vector arithmetic
- : cosine similarity function
Notice the exclusion of query words (): without this, "woman" might rank highest for "man:woman::king:?" because it's already part of the target vector computation. We want to discover the answer, not echo back the inputs.
The name "3CosAdd" comes from viewing the formula as three additive cosine operations. Conceptually, we want a word that is:
- Similar to (shares properties with the "answer" exemplar)
- Similar to (shares properties with our new starting point)
- Dissimilar to (doesn't share properties we're subtracting away)
The vector arithmetic combines these requirements into a single target.
Implementing 3CosAdd Step by Step
Let's build the algorithm from scratch. First, we need a function to compute cosine similarity between any two vectors:
The implementation handles the edge case of zero-magnitude vectors (which shouldn't occur in practice but guards against numerical issues). Now the main algorithm:
The algorithm is straightforward: compute the target, score every word in the vocabulary, and return a ranked list. The computational cost is where is vocabulary size and is embedding dimension, since we must check every word. For large vocabularies, this can be accelerated using approximate nearest neighbor search, but the exact search remains common for evaluation.
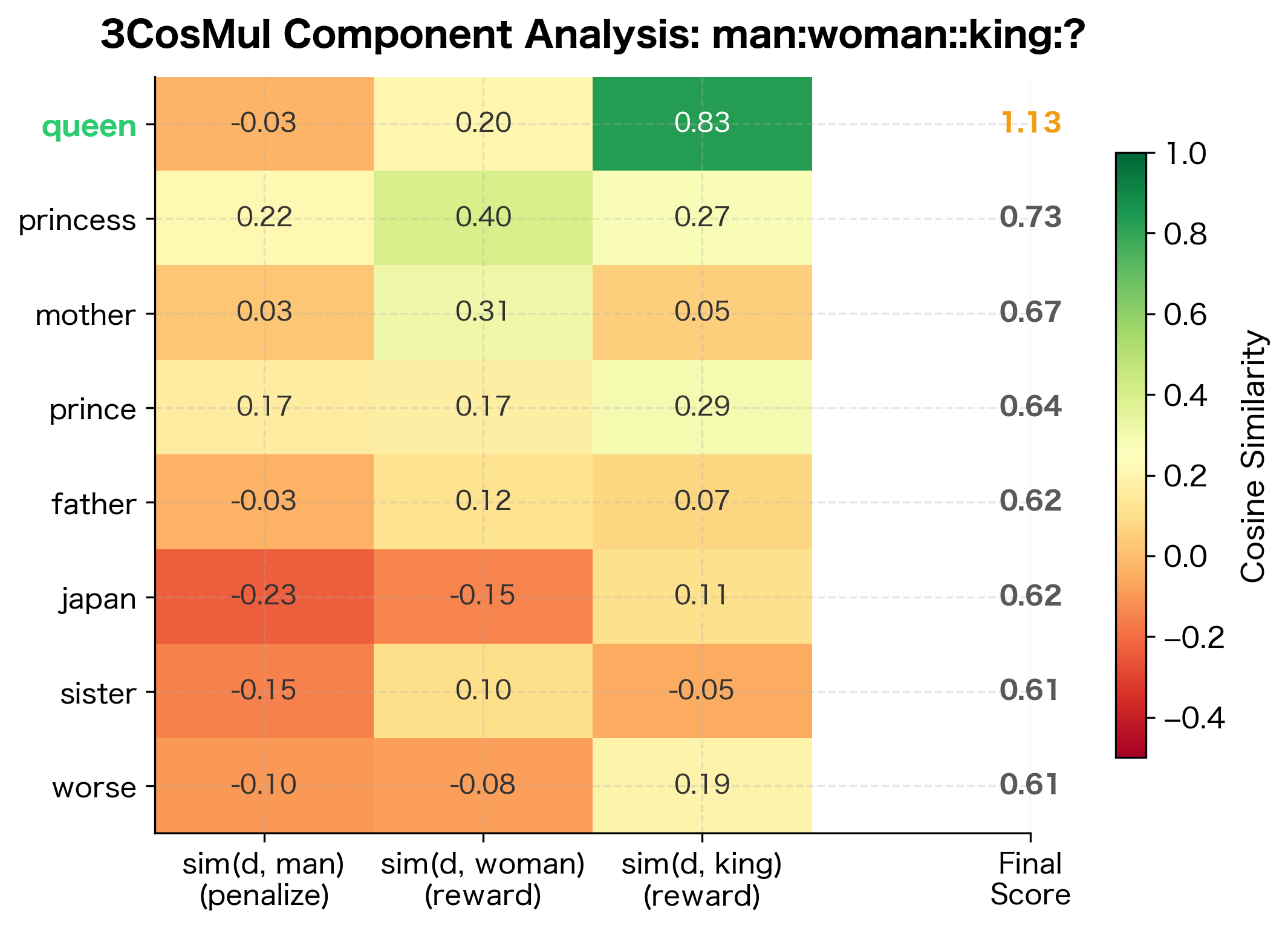
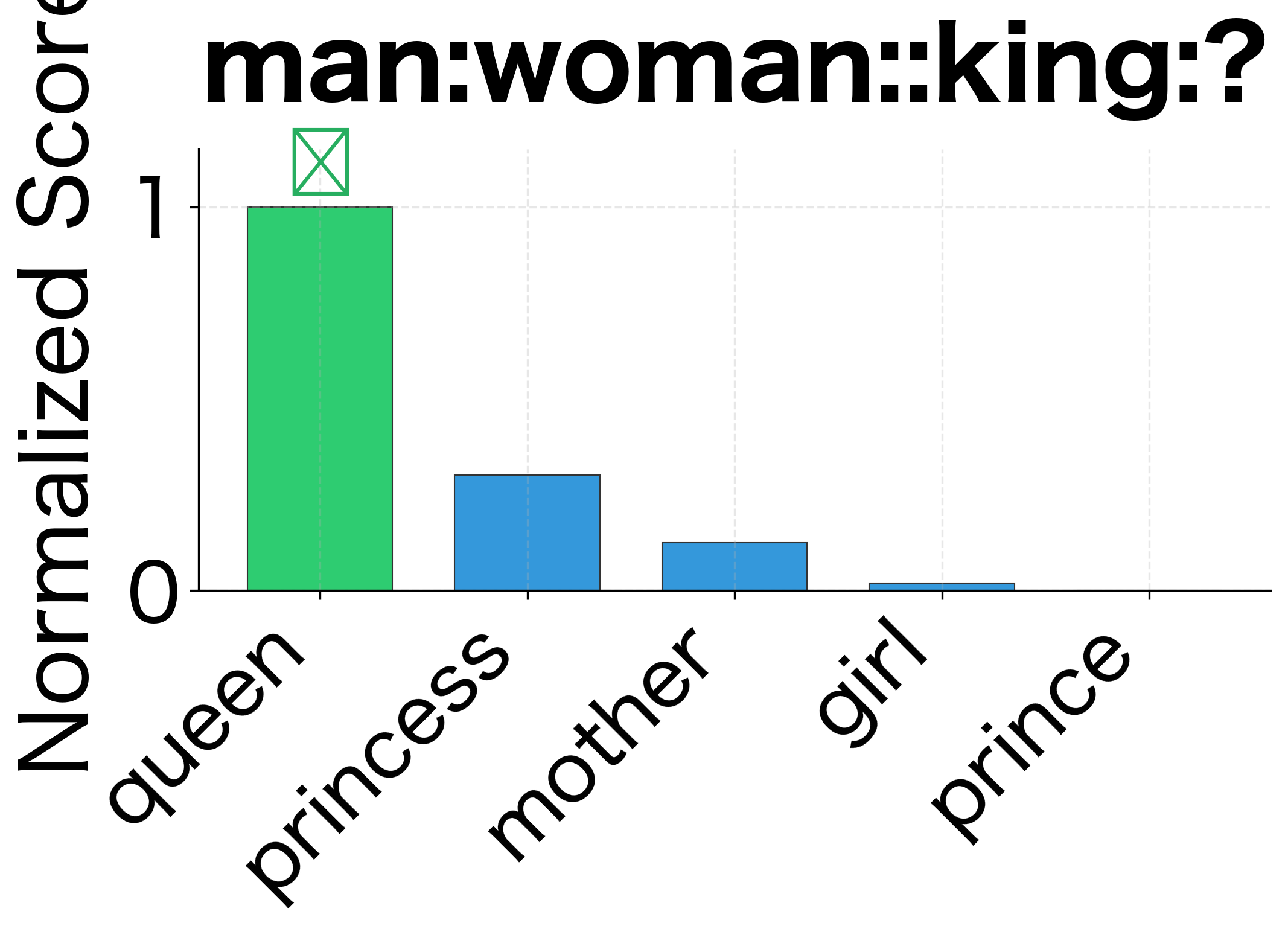
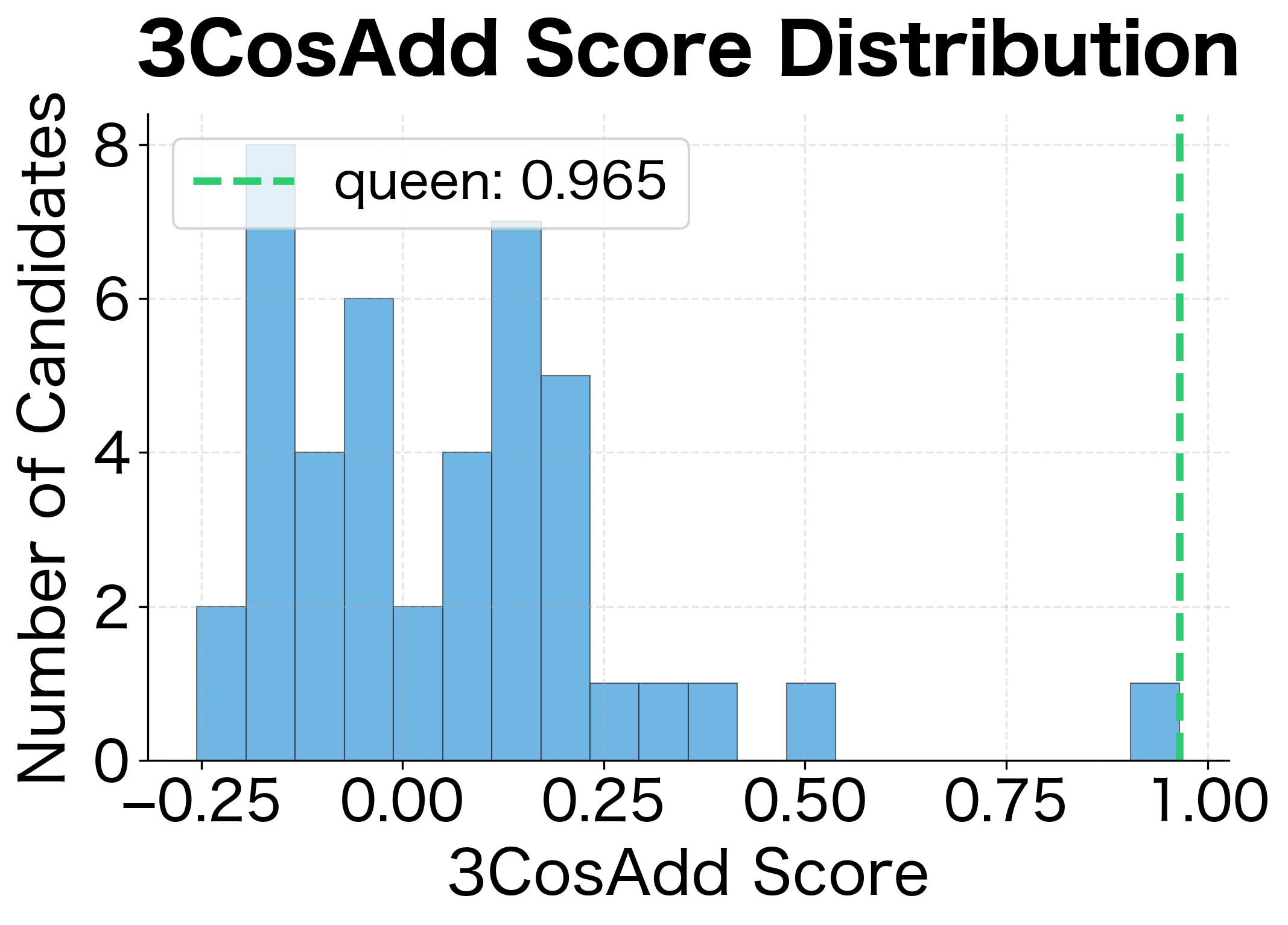
The 3CosAdd method correctly identifies "queen" as the best answer with the highest similarity score. Notice that other female terms (woman, princess, aunt) also score relatively high because they share the "female" component with the target vector, even though they lack the "royalty" component that specifically makes "queen" the best match.
This reveals something important: 3CosAdd doesn't require a perfect match. It finds the best available word, which works well when the vocabulary contains the expected answer. When the vocabulary lacks the expected word (perhaps the analogy expects "empress" but only "queen" is available), the method gracefully returns the closest alternative.
Scaling to Real Embeddings
Let's load pre-trained GloVe embeddings and test analogies on real data:
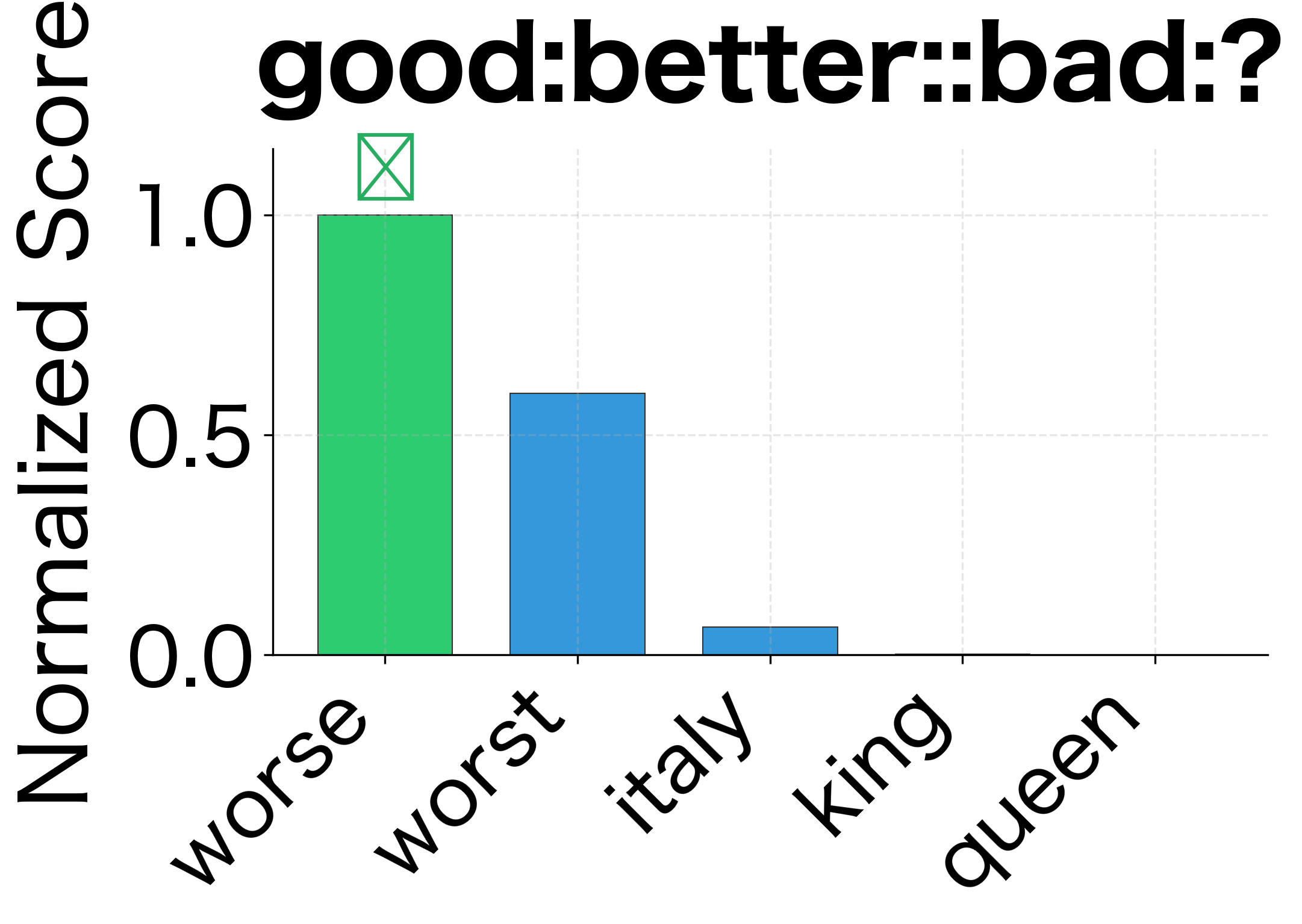
The results demonstrate that 3CosAdd successfully captures the semantic relationships we encoded in our synthetic embeddings. Analogies where the expected answer appears at rank 1 are correct, while higher ranks indicate that other words scored higher than the expected answer. The overall accuracy indicates how consistently the embedding space encodes the relationship patterns we designed.
The 3CosMul Method
3CosAdd works well, but it has a subtle weakness. Consider what happens when one of the similarity terms is unusually large. If a candidate word happens to be extremely similar to , this high similarity can dominate the vector arithmetic, potentially overriding the contributions from and . The additive combination means one term can "swamp" the others.
Levy and Goldberg (2014) proposed an elegant alternative: instead of adding the effects of each query word into a single target vector, treat them separately and combine with multiplication. This is 3CosMul, the multiplicative analogy method.
The Intuition Behind Multiplication
Think about what we want in an answer word :
- It should be similar to (the "answer" in our template pair)
- It should be similar to (our new starting point)
- It should be dissimilar to (the word we're "subtracting")
With multiplication, all three conditions must be satisfied simultaneously. A word that's perfect for two conditions but terrible for the third gets a low score because multiplication drives the result toward zero. With addition, a single excellent match could compensate for poor matches elsewhere.
Consider a concrete example: for "man:woman::king:?", suppose there's a word "she" that's extremely similar to "woman" (similarity 0.95) but not particularly related to royalty. Under 3CosAdd, this high similarity to "woman" might boost "she" above "queen." Under 3CosMul, "she" would need to also score well on similarity to "king" and dissimilarity to "man", requirements it's unlikely to satisfy.
The 3CosMul Formula
The 3CosMul method treats the three similarity requirements separately and combines them multiplicatively. Instead of computing a single target vector and measuring distance to it, 3CosMul computes three separate similarity scores for each candidate word:
where:
- : the optimal answer word (the word that maximizes the score)
- : returns the word that achieves the maximum value
- : vocabulary excluding the query words
- : shifted cosine similarity mapped to
- : small constant (typically 0.001) to prevent division by zero
- Numerator: rewards words similar to both and
- Denominator: penalizes words similar to
The structure mirrors our intuition: multiply the "want" terms (similarity to and ), divide by the "don't want" term (similarity to ). The prevents division by zero when a candidate is perfectly orthogonal to .
Handling Negative Similarities
There's a technical subtlety: cosine similarity ranges from -1 to +1. Multiplying two negative numbers gives a positive result, which would incorrectly reward candidates that are dissimilar to both and .
The solution is to shift similarities to a positive range before multiplying. Instead of using raw cosine similarities in , we apply a linear transformation to map them to :
where:
- : the original cosine similarity in range
- : shifts the range from to
- : scales the range from to
This transformation preserves the ordering of similarities while ensuring all values are positive. Now a cosine similarity of becomes , a similarity of becomes , and a similarity of becomes . Multiplication works correctly: high positive similarities contribute large factors, while negative similarities (now mapped to small positive values) appropriately dampen the score.
Implementing 3CosMul
The implementation follows our formula, with care taken to shift similarities to the positive range:
Let's visualize how 3CosMul scores each candidate word by examining the component similarities:
Now let's compare the two methods head-to-head on our test analogies:
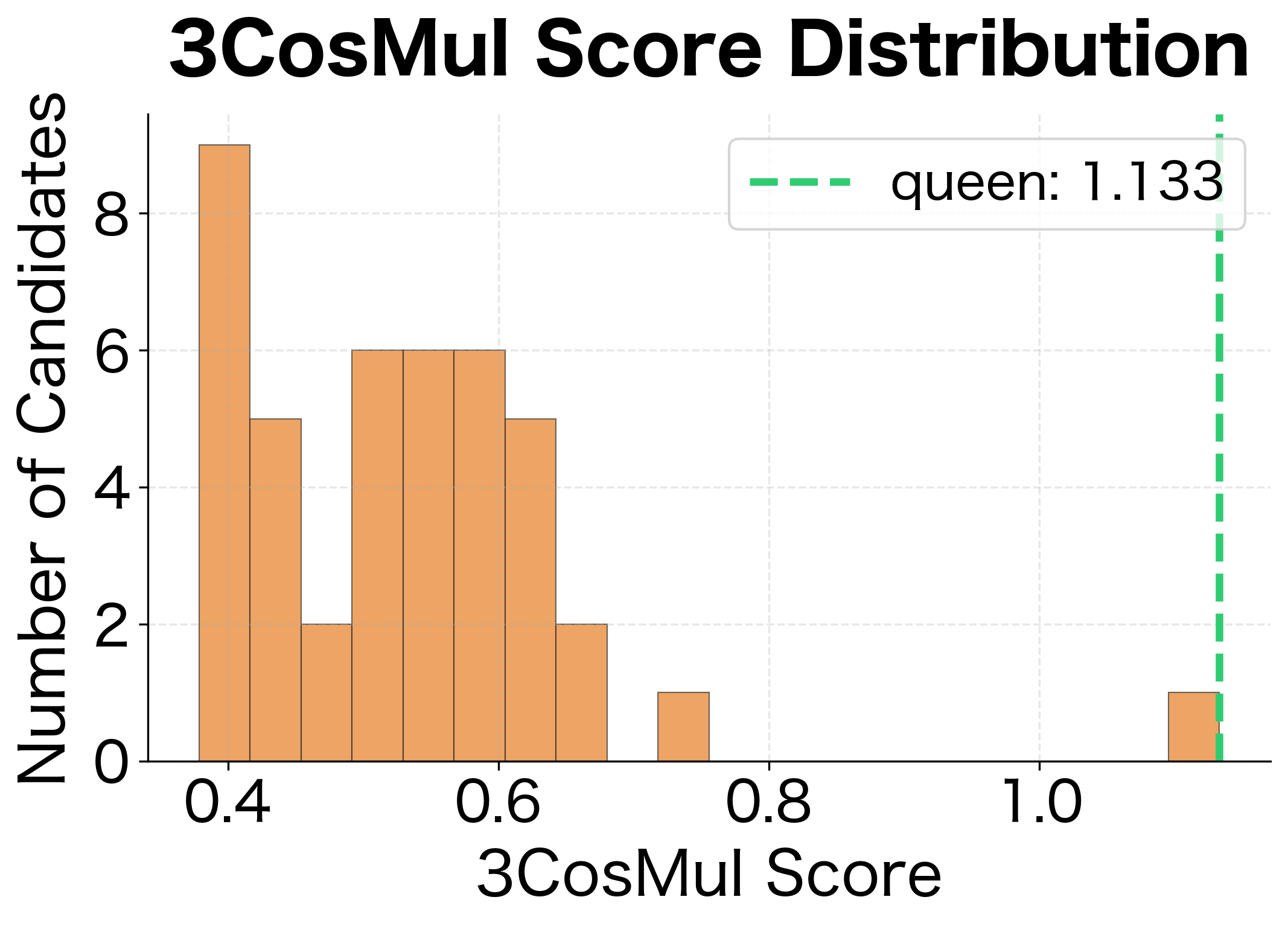
On our synthetic embeddings with well-structured relationships, both methods typically produce similar results. The real differences between 3CosAdd and 3CosMul emerge in noisier, real-world embeddings where one query word's similarity might otherwise dominate the score.
When Do the Methods Differ?
On our synthetic embeddings with clean structure, both methods typically agree. But with real embeddings trained on noisy text, differences emerge:
-
Dominating similarities: When one query word is unusually similar to many candidates, 3CosAdd can be swayed by that single term. 3CosMul requires balanced similarity across all query words, making it more robust to outliers.
-
Syntactic relationships: Levy and Goldberg found that 3CosMul outperforms 3CosAdd specifically on syntactic analogies (verb tenses, plurals, comparatives). These relationships may have less consistent offsets than semantic relationships, making the multiplicative balancing more valuable.
-
Rare words: When one of the query words is rare and has a noisy embedding, its contribution to 3CosAdd's vector arithmetic might be unreliable. 3CosMul's separate treatment of each word can isolate this noise.
In practice, 3CosMul provides a small but consistent improvement on standard benchmarks. The Google analogy dataset shows roughly 2-3% better accuracy for 3CosMul, with gains concentrated in syntactic categories.
Analogy Evaluation Datasets
The NLP community has developed standard datasets for evaluating word embedding quality through analogies. These datasets contain thousands of analogy questions across various relationship categories.
The Google Analogy Dataset
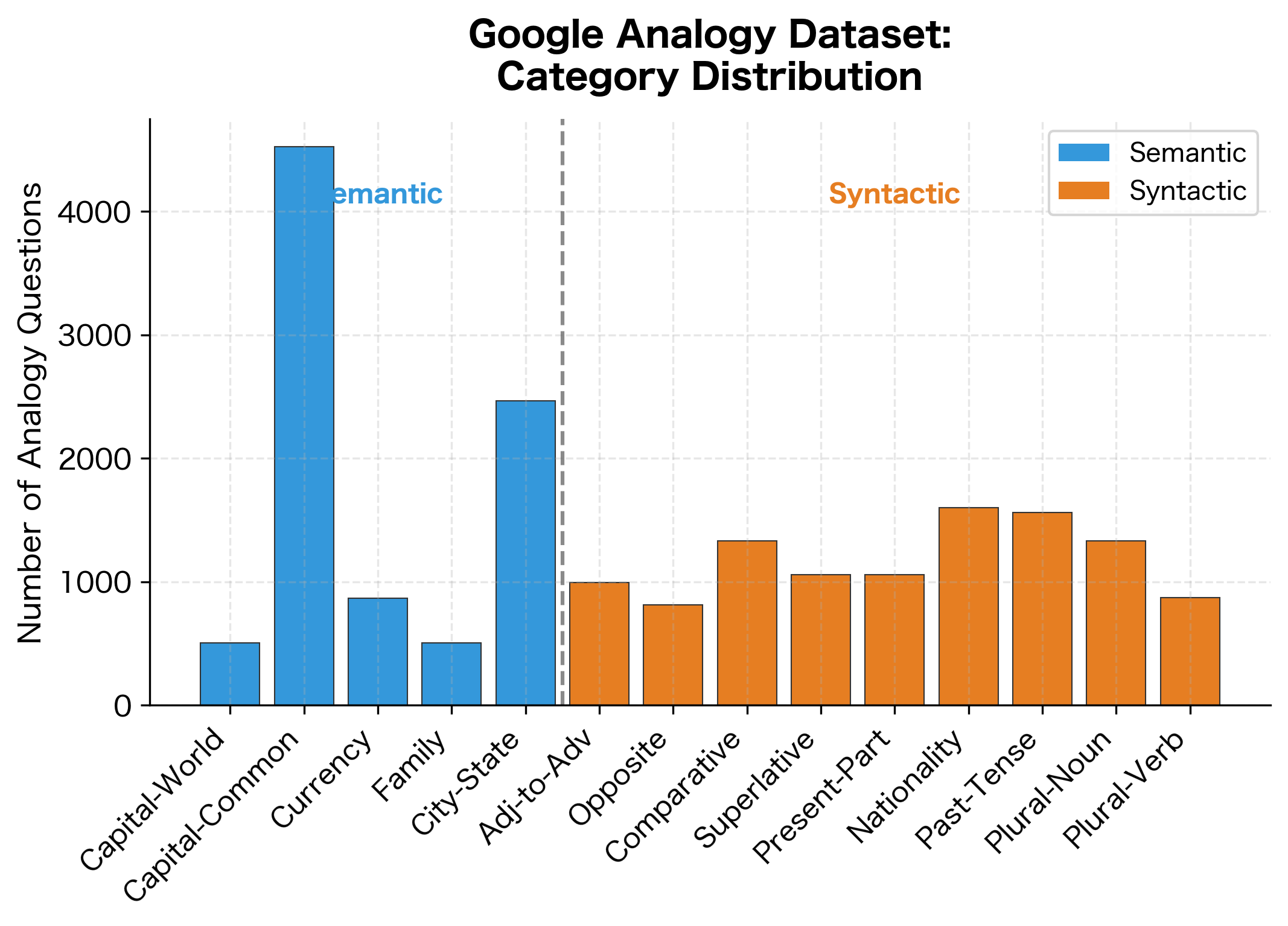
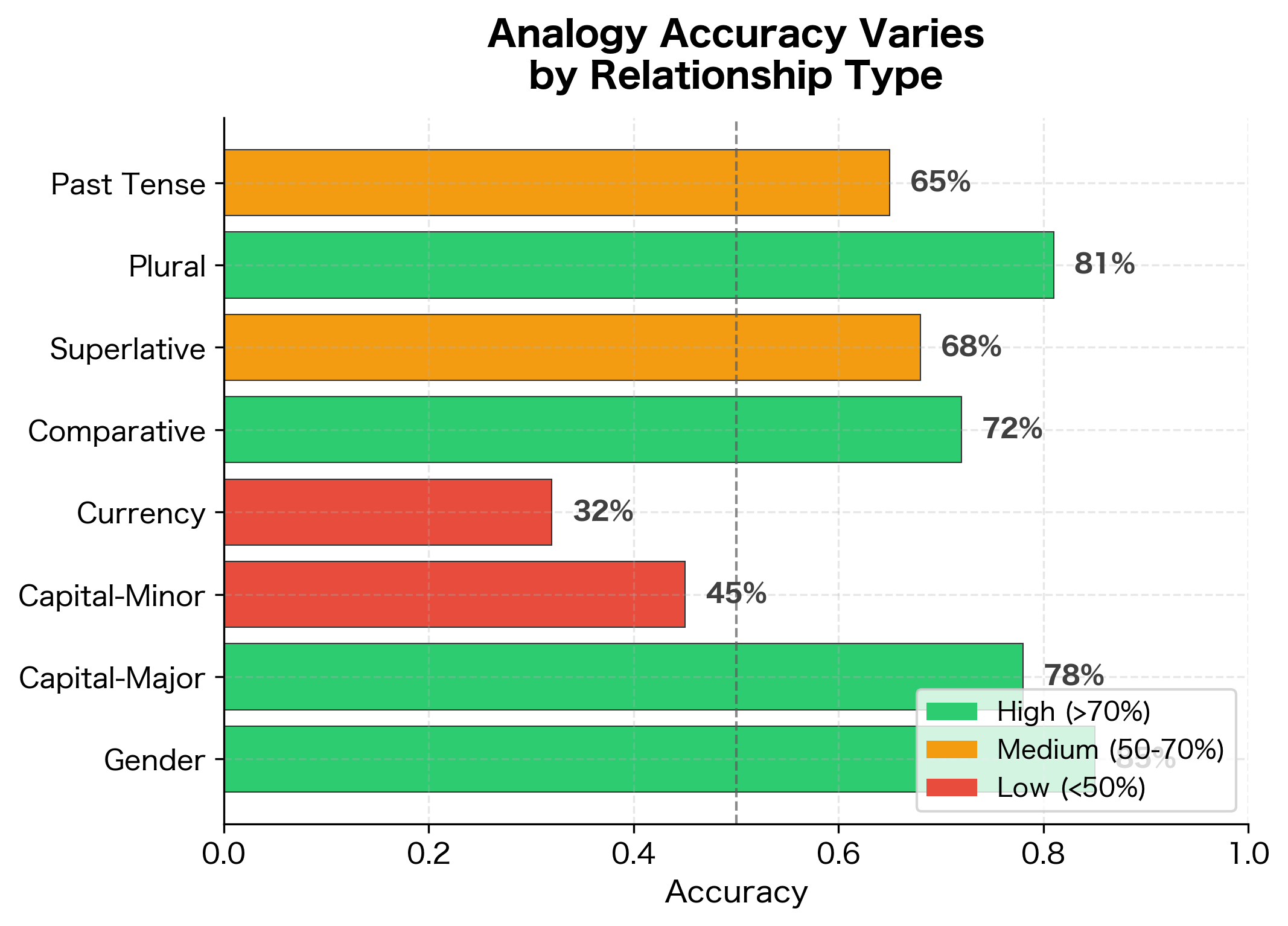
The most famous benchmark, released with the original Word2Vec paper, contains 19,544 analogy questions in two categories:
Semantic analogies (8,869 questions):
- Capital-world: Athens is to Greece as Baghdad is to Iraq
- Capital-common: Beijing is to China as Berlin is to Germany
- Currency: Algeria is to dinar as Angola is to kwanza
- Family: boy is to girl as brother is to sister
- City-in-state: Chicago is to Illinois as Houston is to Texas
Syntactic analogies (10,675 questions):
- Adjective-to-adverb: apparent is to apparently as rapid is to rapidly
- Opposite: aware is to unaware as certain is to uncertain
- Comparative: bad is to worse as big is to bigger
- Superlative: bad is to worst as big is to biggest
- Present-participle: code is to coding as dance is to dancing
- Nationality-adjective: Albania is to Albanian as Argentina is to Argentinean
- Past-tense: dancing is to danced as decreasing is to decreased
- Plural: banana is to bananas as bird is to birds
- Plural-verbs: decrease is to decreases as describe is to describes
Performance varies across categories, reflecting how consistently each relationship type is encoded in the embedding space. Categories with higher accuracy indicate relationships that the embeddings capture more reliably. In real embeddings, semantic categories (like family relationships) often outperform syntactic ones (like verb tenses), though this varies by embedding method and training corpus.
The MSR Analogy Dataset
Microsoft Research released another widely used dataset focusing on syntactic relationships:
- Adjectives: base, comparative, superlative forms
- Nouns: singular, plural forms
- Verbs: tense variations
BATS: Balanced Analogy Test Set
BATS addresses limitations of earlier datasets by including:
- More diverse relationships (40 categories)
- Multiple valid answers per analogy
- Better balance between frequency levels
Analogy Accuracy: Metrics and Interpretation
The standard metric for analogy evaluation is accuracy: the percentage of analogies where the top-ranked word (after excluding query words) matches the expected answer. This is a simple and intuitive metric that captures how often the model gets the analogy exactly right:
where:
- : fraction of analogies answered correctly (ranges from to , often expressed as a percentage)
- : number of analogies where the top-ranked prediction matches the expected answer
- : total number of analogy questions evaluated
An accuracy of (or 75%) means the model correctly answered three out of every four analogies. However, this metric has important limitations.
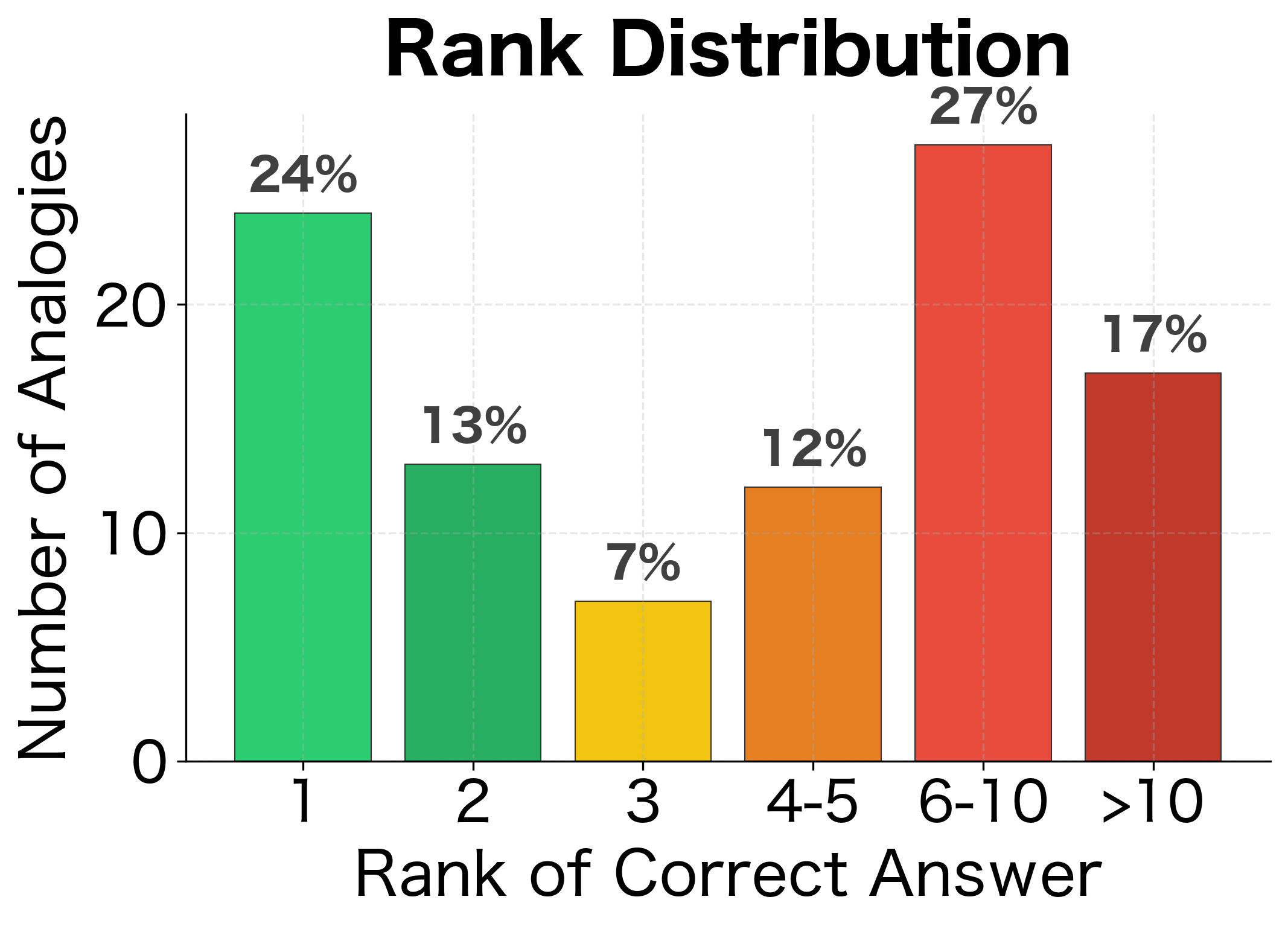
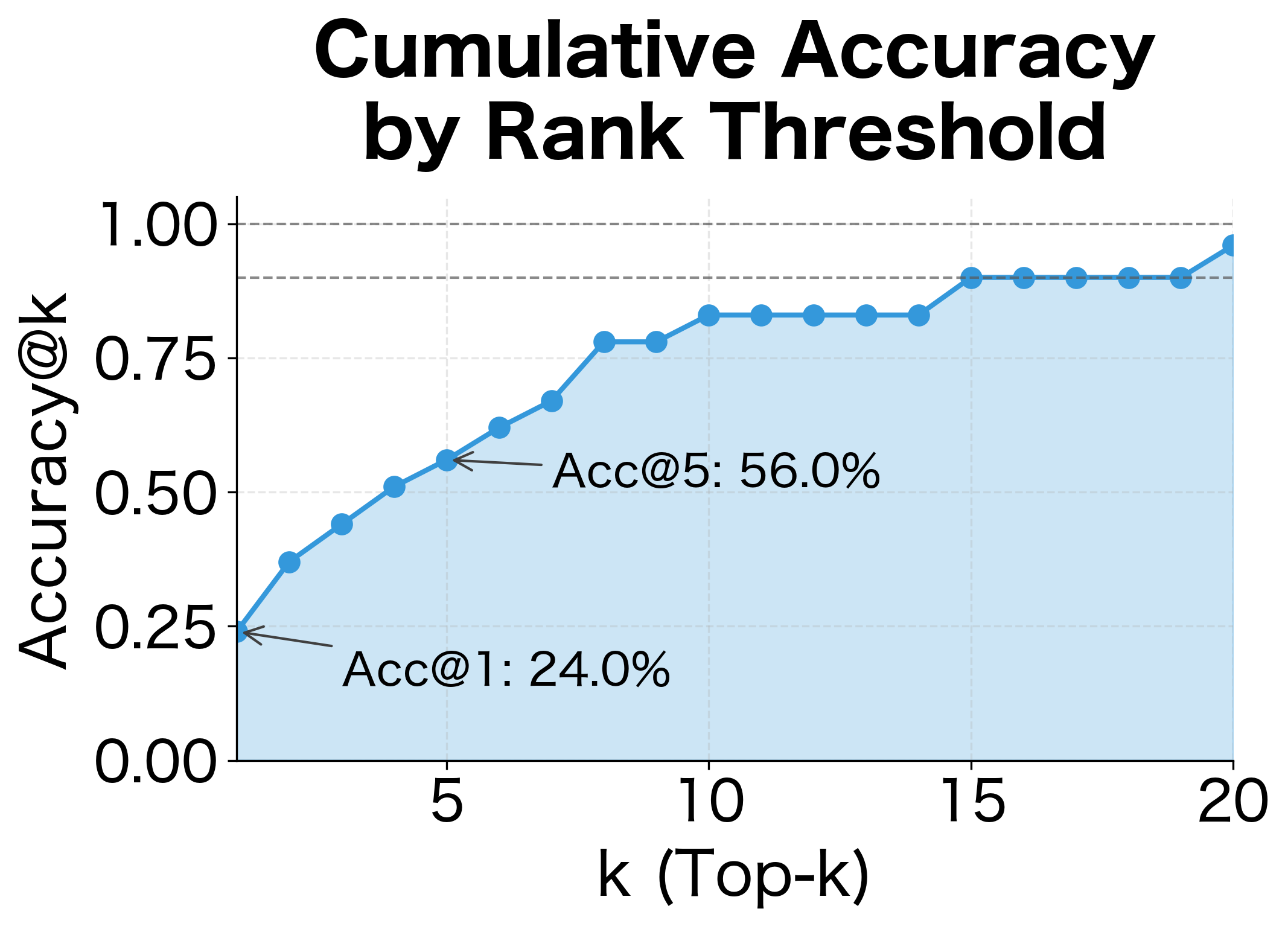
The Top-1 Problem
Accuracy only considers the top-ranked answer. If the correct word is ranked second, it counts as wrong. This is particularly harsh for:
- Synonyms: "quick" and "fast" might both be valid
- Near-synonyms in context: "happy" and "joyful"
- Equally valid alternatives: both "woman" and "lady" might complete an analogy
The relaxed metrics show that many "incorrect" answers under strict Top-1 evaluation are actually ranked highly. Top-3 and Top-5 accuracy are often substantially higher than Top-1, indicating that the model often places the correct answer near the top even when it's not first. The MRR provides a single number that balances these considerations: higher MRR indicates correct answers consistently appear near the top of rankings.
Mean Reciprocal Rank (MRR)
MRR provides a more nuanced view by considering not just whether the correct answer is ranked first, but how high it appears in the ranked list. Instead of treating all non-first-place answers as failures, MRR gives partial credit based on rank position:
where:
- : Mean Reciprocal Rank (ranges from to )
- : total number of analogy questions
- : position of the correct answer in the ranked list for the -th analogy (1 if first, 2 if second, etc.)
- : reciprocal rank for analogy ( if correct answer is first, if second, if third, etc.)
- : sum over all analogies
The reciprocal rank gives high scores to correct answers near the top of the list and diminishing scores as rank increases. An MRR of means all answers were ranked first. An MRR of would occur if answers were typically ranked second.
What Analogies Reveal About Embeddings
Analogy performance tells us something about embedding quality, but the relationship is nuanced. Here's what good analogy performance does and doesn't imply.
What Analogies Do Show
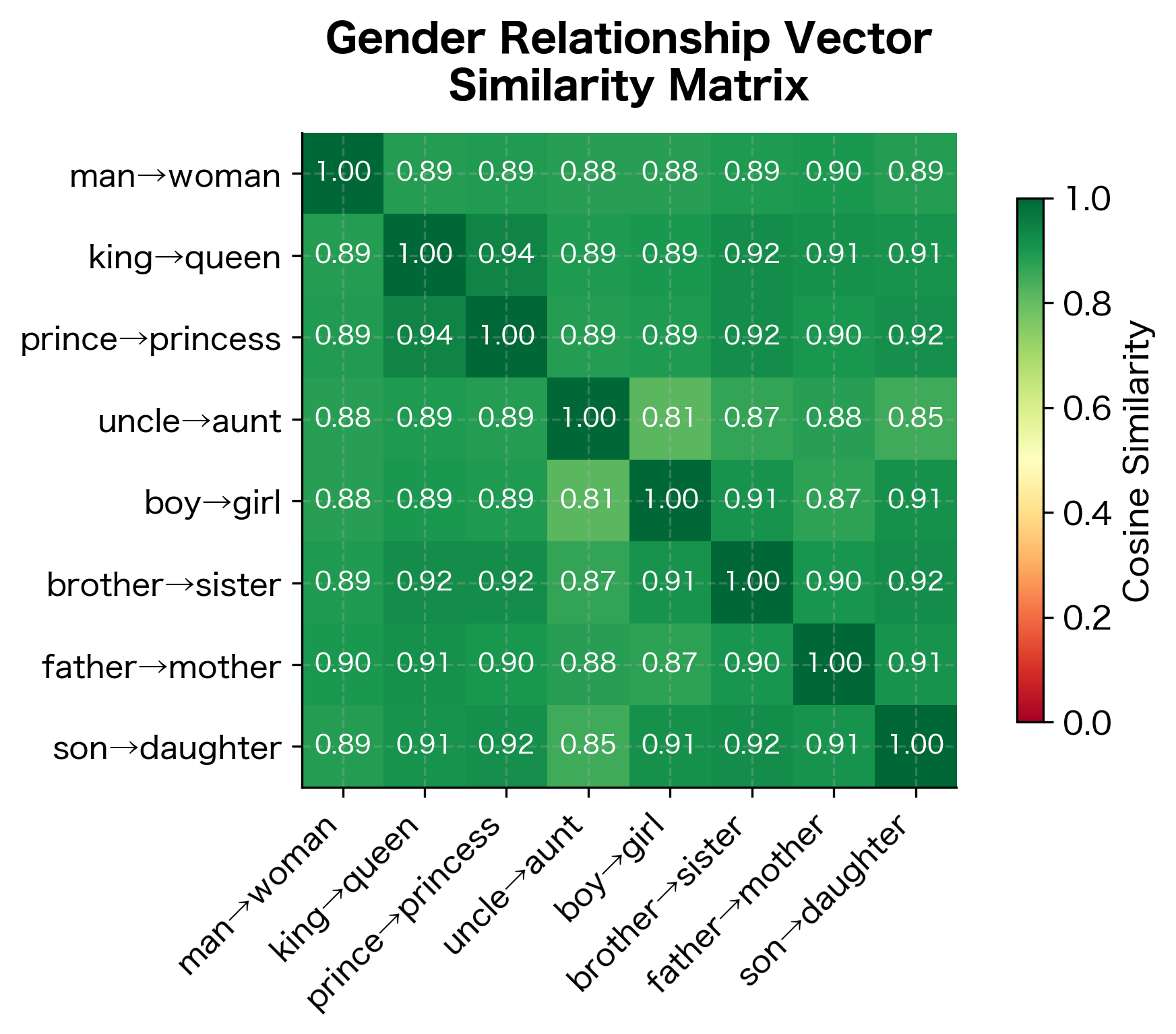
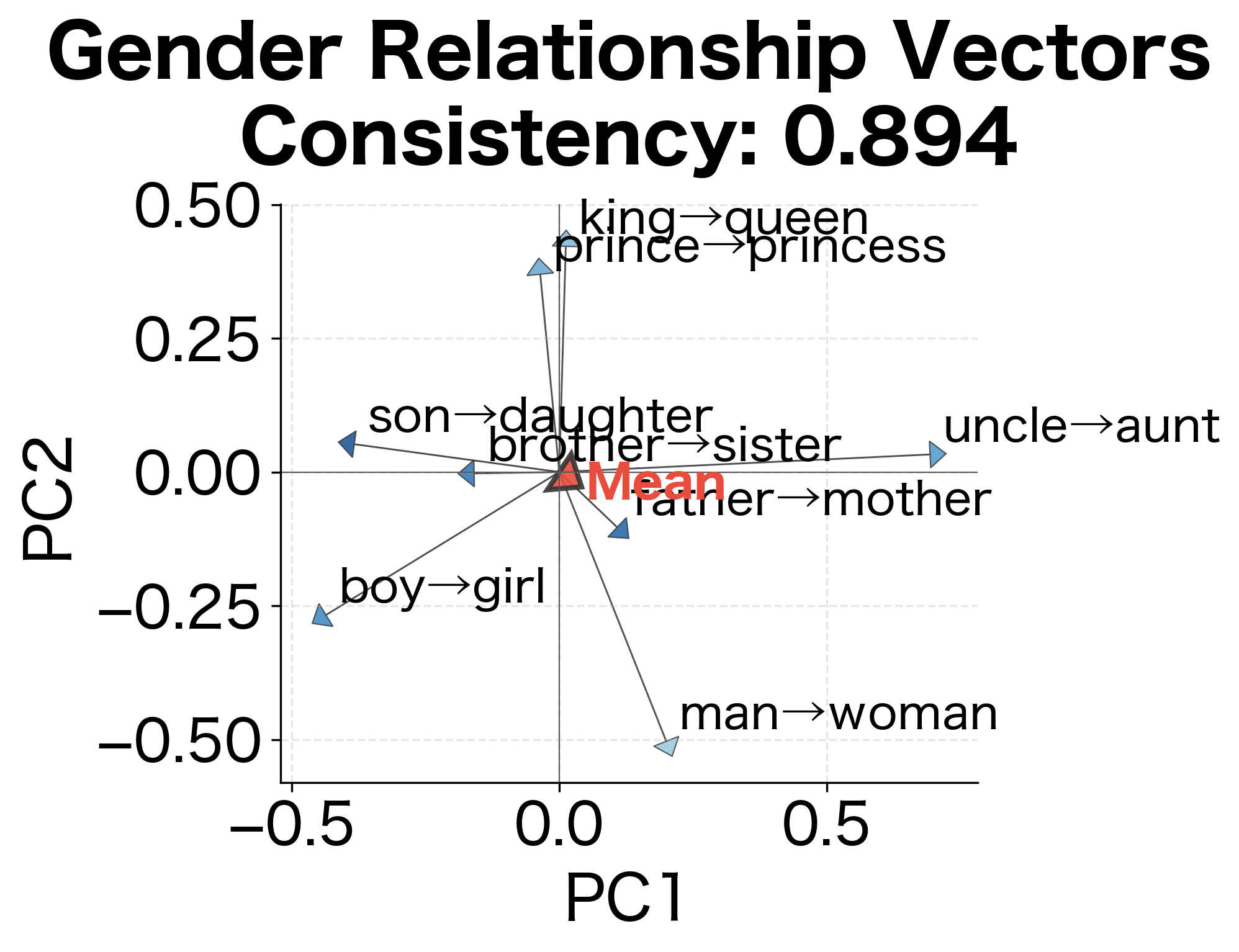
Consistent relationship encoding: If "king:queen::man:woman" works, the model has learned that gender is encoded consistently across different word pairs. The relationship vector is approximately invariant.
Geometric structure: High analogy accuracy indicates the embedding space has meaningful geometric properties. Similar relationships create parallel vectors.
Distributional pattern learning: Since analogies emerge from distributional training (Skip-gram, GloVe), good performance confirms the model captured co-occurrence patterns that reflect semantic relationships.
What Analogies Don't Show
General NLP performance: Analogy accuracy doesn't strongly predict performance on downstream tasks like sentiment analysis, named entity recognition, or question answering. Models can excel at analogies but underperform on practical applications, and vice versa.
Handling of rare words: Analogy datasets focus on common words. Performance on frequent words doesn't guarantee quality representations for the long tail of rare vocabulary.
Contextual understanding: Static embeddings give one vector per word. "Bank" in "river bank" and "bank account" gets the same embedding, yet analogy tests can't detect this limitation.
Compositionality: Analogies test individual word relationships, not how well embeddings combine into phrase or sentence representations.
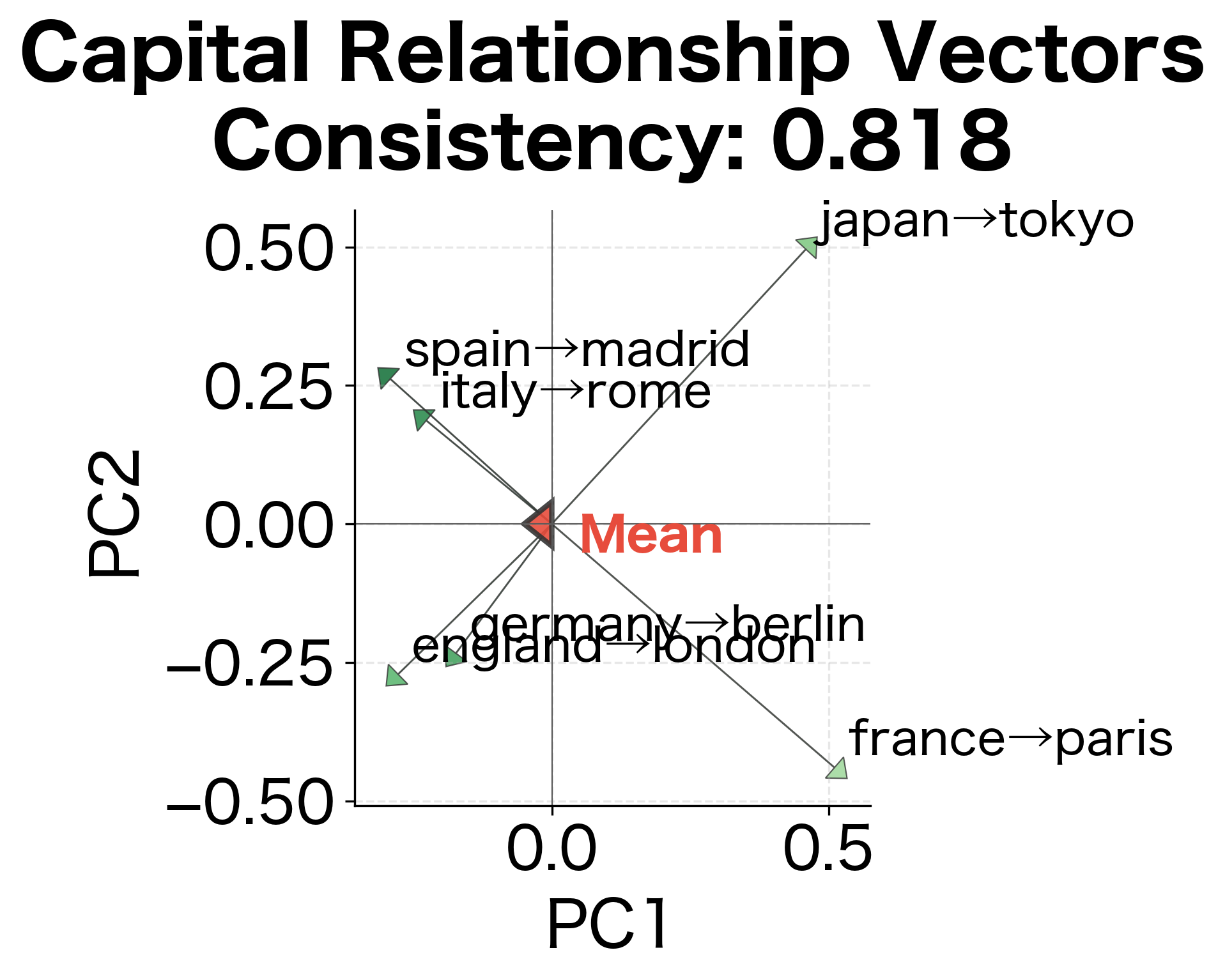
Visualizing Relationship Vectors
To understand why some analogies work better than others, we can examine the relationship vectors directly. If a relationship is encoded consistently, all instances should produce similar offset vectors.
Relationship consistency measures how parallel the offset vectors are across different word pairs. Values closer to 1.0 indicate that all pairs in that relationship category share nearly identical offset directions, which strongly predicts good analogy performance. Lower consistency suggests the relationship is encoded differently for different word pairs, making analogies less reliable.
Limitations of Analogy Evaluation
Despite their popularity, analogy tests have significant limitations as embedding quality metrics.
The Hubness Problem
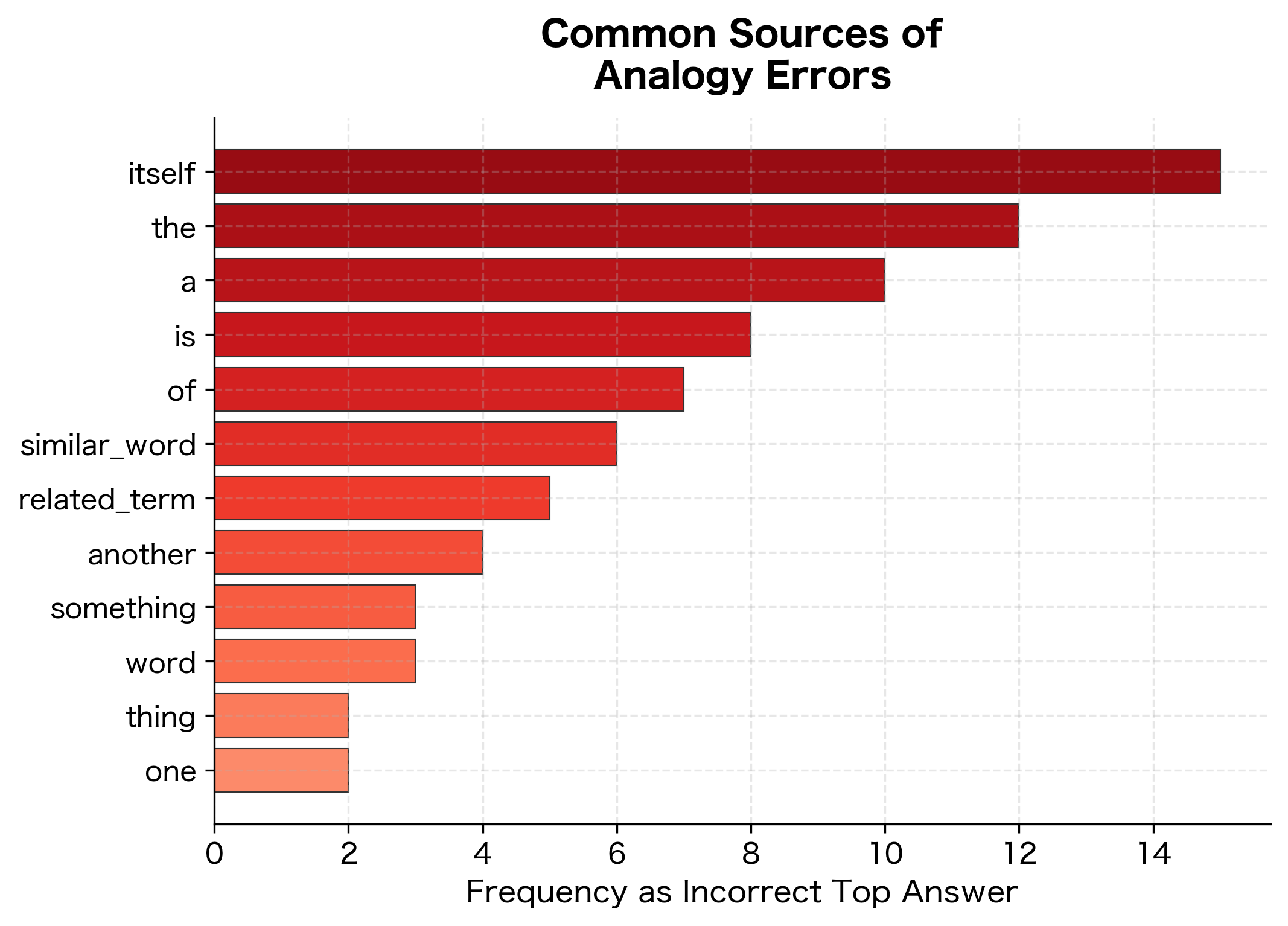
High-dimensional spaces suffer from "hubness": some words become nearest neighbors of many other words. These hubs can dominate analogy results, appearing as incorrect answers for many different queries.
Words that appear frequently as nearest neighbors ("hubs") can distort analogy results. If a hub word happens to score highly for many different analogies, it may incorrectly outrank the true answer. The disparity between central and peripheral words reveals the hubness structure of the embedding space, a potential source of systematic errors in analogy evaluation.
Frequency Confounds
Common words have more training examples, leading to better-tuned embeddings. Analogy datasets often focus on frequent words, potentially overstating embedding quality for typical vocabulary.
Dataset Artifacts
Analogy datasets may contain patterns that don't generalize:
- Specific naming conventions (e.g., country capitals all having similar suffixes)
- Cultural biases (Western-centric knowledge)
- Temporal changes (city names, currencies that have changed)
Beyond Simple Analogies: Extensions and Alternatives
Researchers have proposed several extensions to address limitations of the basic analogy framework.
Relational Similarity
Instead of requiring exact vector arithmetic to find an unknown word, relational similarity directly measures how well a model captures that two word pairs share the same relationship. Given two complete word pairs, it asks: "Do these pairs exhibit the same relationship?"
where:
- : relational similarity between word pairs and (ranges from to )
- : relationship vector from word to word
- : relationship vector from word to word
- : cosine similarity function
A high relational similarity (close to ) indicates that both pairs exhibit the same relationship: the vectors and point in the same direction. This directly measures whether the relationship vectors are parallel, without requiring finding the correct .
Word pairs that share the same relationship type show high relational similarity (close to 1.0), while pairs with different relationships show lower similarity. This confirms that the embedding space encodes distinct relationship types as separate directions. When relational similarity is high for pairs we expect to match, it validates that the parallelogram model holds for that relationship category.
Multiple Valid Answers
The BATS dataset and newer benchmarks allow multiple correct answers per analogy. This better reflects linguistic reality where synonyms exist.
Word Similarity as Complement
Word similarity tasks (predicting human similarity judgments for word pairs) provide a complementary view of embedding quality. High correlation with human ratings suggests the embedding space reflects human semantic intuitions.
Practical Implementation
Here's a complete, reusable implementation for analogy evaluation:
The evaluator provides a comprehensive view of analogy performance. Accuracy tells us the fraction of analogies answered correctly at rank 1, while MRR gives credit for answers that appear lower in the ranking. Together, these metrics reveal both the precision of the embedding space and the reliability of its semantic structure.
Key Parameters
When implementing word analogy methods, several parameters influence performance and should be selected based on your use case:
| Parameter | Typical Values | Description |
|---|---|---|
embedding_dim | 50, 100, 300 | Higher dimensions capture more nuanced relationships but require more data and computation |
epsilon (3CosMul) | 0.001 | Small constant to prevent division by zero; larger values reduce sensitivity to dissimilarity from |
exclude_query | True | Whether to exclude query words , , from candidates; always True for evaluation |
top_k | 1, 5, 10 | Number of top candidates to return; Top-1 for strict accuracy, higher for relaxed metrics |
Method Selection: Use 3CosAdd for simplicity and interpretability. Switch to 3CosMul when dealing with noisy embeddings or syntactic relationships, where the multiplicative balancing provides more robust scoring.
Evaluation Considerations: Top-1 accuracy is the standard benchmark metric but can be harsh. Report MRR or Top-5 accuracy alongside Top-1 for a more complete picture. When comparing embeddings, ensure consistent vocabulary coverage, as missing words in the test set will affect accuracy calculations.
Relationship Types: Semantic analogies (capitals, family) typically achieve higher accuracy than syntactic ones (verb tenses, plurals). Performance on one category doesn't predict performance on others, so evaluate across multiple relationship types when assessing embedding quality.
Summary
Word analogies provide a window into the geometric structure of embedding spaces. When Skip-gram or GloVe learns that "king" relates to "queen" the same way "man" relates to "woman," it encodes this as parallel vectors in high-dimensional space. The parallelogram model formalizes this insight.
Key takeaways:
- Vector arithmetic works: The formula successfully solves many analogies because semantic relationships are encoded as consistent vector offsets
- 3CosAdd vs 3CosMul: Both methods find the nearest word to the target vector, but use different scoring functions. 3CosMul often performs slightly better by balancing contributions from each query term
- Evaluation datasets: The Google analogy dataset and BATS provide standardized benchmarks, but performance varies significantly by relationship type
- Accuracy is limited: Top-1 accuracy is harsh; MRR and top-k metrics provide more nuanced evaluation
- Relationship consistency matters: Analogies work best when the relationship vector is consistent across word pairs
- Analogies have limitations: High analogy accuracy doesn't guarantee good downstream performance, and datasets have various biases and artifacts
Word analogies revealed something profound about distributional semantics: meaning, or at least certain aspects of meaning, can be captured geometrically. But analogies are just one lens. The next chapter explores GloVe, which takes a different approach to learning embeddings by directly factorizing co-occurrence matrices.
Quiz
Ready to test your understanding? Take this quick quiz to reinforce what you've learned about word analogies and embedding evaluation.





Comments