Copy Mechanism: Pointer Networks for Neural Text Generation

Michael Brenndoerfer

Language AI Handbook Machine Learning deep-learning natural-language-processing

Learn how copy mechanisms enable seq2seq models to handle out-of-vocabulary words by copying tokens directly from input, with pointer-generator networks and coverage.

Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Copy MechanismLink Copied

Standard sequence-to-sequence models generate output tokens by selecting from a fixed vocabulary. This works well for common words, but what happens when the input contains a rare proper name, a technical term, or a number that the model has never seen? The decoder must either hallucinate a substitute or produce a generic placeholder. Neither outcome is satisfactory.

Copy mechanisms solve this problem by allowing the decoder to directly copy tokens from the input sequence. Instead of being forced to generate every output token from scratch, the model can "point" to input positions and reproduce those tokens verbatim. This matters for tasks like summarization, where preserving names and facts is critical, and for handling out-of-vocabulary words that would otherwise be lost.

This chapter explores how copy mechanisms work, from the foundational pointer networks to the practical pointer-generator architecture. You'll learn how models compute copy probabilities, blend copying with generation, and handle the challenging case of out-of-vocabulary tokens. By the end, you'll understand why copy mechanisms became a standard component in production summarization systems.

The Vocabulary Problem in GenerationLink Copied

Before diving into copy mechanisms, let's understand the problem they solve. Traditional seq2seq models have a fixed output vocabulary, typically the most frequent words in the training data.

In[2]:

Code

from collections import Counter

# Simulate a typical vocabulary scenario
training_corpus = """
The president announced new policies today.
Scientists discovered a breakthrough in medicine.
The company reported strong quarterly earnings.
Researchers published findings in Nature journal.
The government proposed infrastructure spending.
"""

# Build vocabulary from training data
words = training_corpus.lower().split()
word_counts = Counter(words)

# Typical vocab: keep only frequent words
vocab_size = 20
vocab = ["<unk>", "<sos>", "<eos>"] + [
    word for word, _ in word_counts.most_common(vocab_size - 3)
]
word_to_idx = {word: i for i, word in enumerate(vocab)}

from collections import Counter

# Simulate a typical vocabulary scenario
training_corpus = """
The president announced new policies today.
Scientists discovered a breakthrough in medicine.
The company reported strong quarterly earnings.
Researchers published findings in Nature journal.
The government proposed infrastructure spending.
"""

# Build vocabulary from training data
words = training_corpus.lower().split()
word_counts = Counter(words)

# Typical vocab: keep only frequent words
vocab_size = 20
vocab = ["<unk>", "<sos>", "<eos>"] + [
    word for word, _ in word_counts.most_common(vocab_size - 3)
]
word_to_idx = {word: i for i, word in enumerate(vocab)}

Out[3]:

Console

Vocabulary Construction
==================================================

Vocabulary size: 20

Top words in vocab:
  <unk>
  <sos>
  <eos>
  the
  in
  president
  announced
  new
  policies
  today.
  ...

Now consider what happens when we encounter input with rare words:

In[4]:

Code

# Input with rare/unseen words
test_input = "Dr. Nakamura presented findings at the Stanford conference."

# Check which words are in vocabulary
in_vocab = []
out_of_vocab = []

for word in test_input.lower().replace(".", "").split():
    if word in word_to_idx:
        in_vocab.append(word)
    else:
        out_of_vocab.append(word)

# Input with rare/unseen words
test_input = "Dr. Nakamura presented findings at the Stanford conference."

# Check which words are in vocabulary
in_vocab = []
out_of_vocab = []

for word in test_input.lower().replace(".", "").split():
    if word in word_to_idx:
        in_vocab.append(word)
    else:
        out_of_vocab.append(word)

Out[5]:

Console

Out-of-Vocabulary Analysis
==================================================

Input: Dr. Nakamura presented findings at the Stanford conference.

In vocabulary: ['the']
Out of vocabulary (OOV): ['dr', 'nakamura', 'presented', 'findings', 'at', 'stanford', 'conference']

OOV rate: 87.5%

The words "Nakamura," "Stanford," and "conference" are critical for an accurate summary, yet a standard decoder cannot produce them. It would have to replace them with <unk> tokens or substitute similar but incorrect words. Copy mechanisms solve this directly: let the decoder point to these words in the input and copy them.

Pointer Networks: The FoundationLink Copied

To understand copy mechanisms, we must first grapple with a fundamental question: how can a neural network select items from a variable-length input sequence? Traditional neural networks produce outputs of fixed size, but when copying from input, we need to point to one of $n$ positions where $n$ changes with each input.

Pointer networks, introduced by Vinyals et al. in 2015, solve this by repurposing attention. Recall that attention computes a weighted combination of encoder states, producing weights that sum to 1 across all input positions. These weights already form a probability distribution over the input. The key insight is simple: instead of using attention weights only to compute context vectors, we can interpret them directly as "pointing" probabilities.

Pointer Network

A pointer network is a sequence-to-sequence model where the output at each step is a pointer to an element in the input sequence. Instead of generating tokens from a vocabulary, it uses attention over the input to select which input position to "point to."

Let's trace through the mechanics. At each decoder step, we have a decoder hidden state $s_t$ that encodes what we've generated so far. We also have encoder outputs $h_1, h_2, \ldots, h_n$ representing each input position. The pointer mechanism computes a score for each input position, measuring how relevant that position is given the current decoder state:

Project both representations into a common space using learned weight matrices
Combine them through addition (Bahdanau-style) and pass through a nonlinearity
Compute a scalar score for each position using a learned vector
Normalize with softmax to obtain a valid probability distribution

The resulting probabilities tell us: "Given what I've generated so far, how likely should I point to each input position?"

In[6]:

Code

import torch
import torch.nn as nn
import torch.nn.functional as F


class PointerAttention(nn.Module):
    """
    Attention mechanism that produces pointer probabilities.
    """

    def __init__(self, hidden_dim):
        super().__init__()
        self.hidden_dim = hidden_dim

        # Attention parameters (Bahdanau-style)
        self.W_encoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_decoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.v = nn.Linear(hidden_dim, 1, bias=False)

    def forward(self, decoder_state, encoder_outputs, mask=None):
        """
        Compute pointer probabilities over input positions.

        Args:
            decoder_state: (batch, hidden_dim)
            encoder_outputs: (batch, seq_len, hidden_dim)
            mask: (batch, seq_len) - True for valid positions

        Returns:
            pointer_probs: (batch, seq_len) - probability of pointing to each input
        """
        batch_size, seq_len, _ = encoder_outputs.shape

        # Project encoder outputs: (batch, seq_len, hidden)
        encoder_proj = self.W_encoder(encoder_outputs)

        # Project decoder state: (batch, hidden) -> (batch, 1, hidden)
        decoder_proj = self.W_decoder(decoder_state).unsqueeze(1)

        # Compute attention scores: (batch, seq_len, 1) -> (batch, seq_len)
        scores = self.v(torch.tanh(encoder_proj + decoder_proj)).squeeze(-1)

        # Apply mask (set invalid positions to -inf)
        if mask is not None:
            scores = scores.masked_fill(~mask, float("-inf"))

        # Softmax to get pointer probabilities
        pointer_probs = F.softmax(scores, dim=-1)

        return pointer_probs


# Create example
hidden_dim = 64
batch_size = 2
seq_len = 5

attention = PointerAttention(hidden_dim)
decoder_state = torch.randn(batch_size, hidden_dim)
encoder_outputs = torch.randn(batch_size, seq_len, hidden_dim)
mask = torch.ones(batch_size, seq_len, dtype=torch.bool)

pointer_probs = attention(decoder_state, encoder_outputs, mask)

import torch
import torch.nn as nn
import torch.nn.functional as F


class PointerAttention(nn.Module):
    """
    Attention mechanism that produces pointer probabilities.
    """

    def __init__(self, hidden_dim):
        super().__init__()
        self.hidden_dim = hidden_dim

        # Attention parameters (Bahdanau-style)
        self.W_encoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_decoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.v = nn.Linear(hidden_dim, 1, bias=False)

    def forward(self, decoder_state, encoder_outputs, mask=None):
        """
        Compute pointer probabilities over input positions.

        Args:
            decoder_state: (batch, hidden_dim)
            encoder_outputs: (batch, seq_len, hidden_dim)
            mask: (batch, seq_len) - True for valid positions

        Returns:
            pointer_probs: (batch, seq_len) - probability of pointing to each input
        """
        batch_size, seq_len, _ = encoder_outputs.shape

        # Project encoder outputs: (batch, seq_len, hidden)
        encoder_proj = self.W_encoder(encoder_outputs)

        # Project decoder state: (batch, hidden) -> (batch, 1, hidden)
        decoder_proj = self.W_decoder(decoder_state).unsqueeze(1)

        # Compute attention scores: (batch, seq_len, 1) -> (batch, seq_len)
        scores = self.v(torch.tanh(encoder_proj + decoder_proj)).squeeze(-1)

        # Apply mask (set invalid positions to -inf)
        if mask is not None:
            scores = scores.masked_fill(~mask, float("-inf"))

        # Softmax to get pointer probabilities
        pointer_probs = F.softmax(scores, dim=-1)

        return pointer_probs


# Create example
hidden_dim = 64
batch_size = 2
seq_len = 5

attention = PointerAttention(hidden_dim)
decoder_state = torch.randn(batch_size, hidden_dim)
encoder_outputs = torch.randn(batch_size, seq_len, hidden_dim)
mask = torch.ones(batch_size, seq_len, dtype=torch.bool)

pointer_probs = attention(decoder_state, encoder_outputs, mask)

Out[7]:

Console

Pointer Attention Output
==================================================

Input sequence length: 5

Pointer probabilities (batch 0):
  Position 0: 0.241 ███████
  Position 1: 0.205 ██████
  Position 2: 0.171 █████
  Position 3: 0.192 █████
  Position 4: 0.191 █████

Sum of probabilities: 1.0000

The pointer probabilities form a valid distribution over input positions. At each decoding step, the model can select which input token to copy by sampling from or taking the argmax of this distribution.

Computing the Copy ProbabilityLink Copied

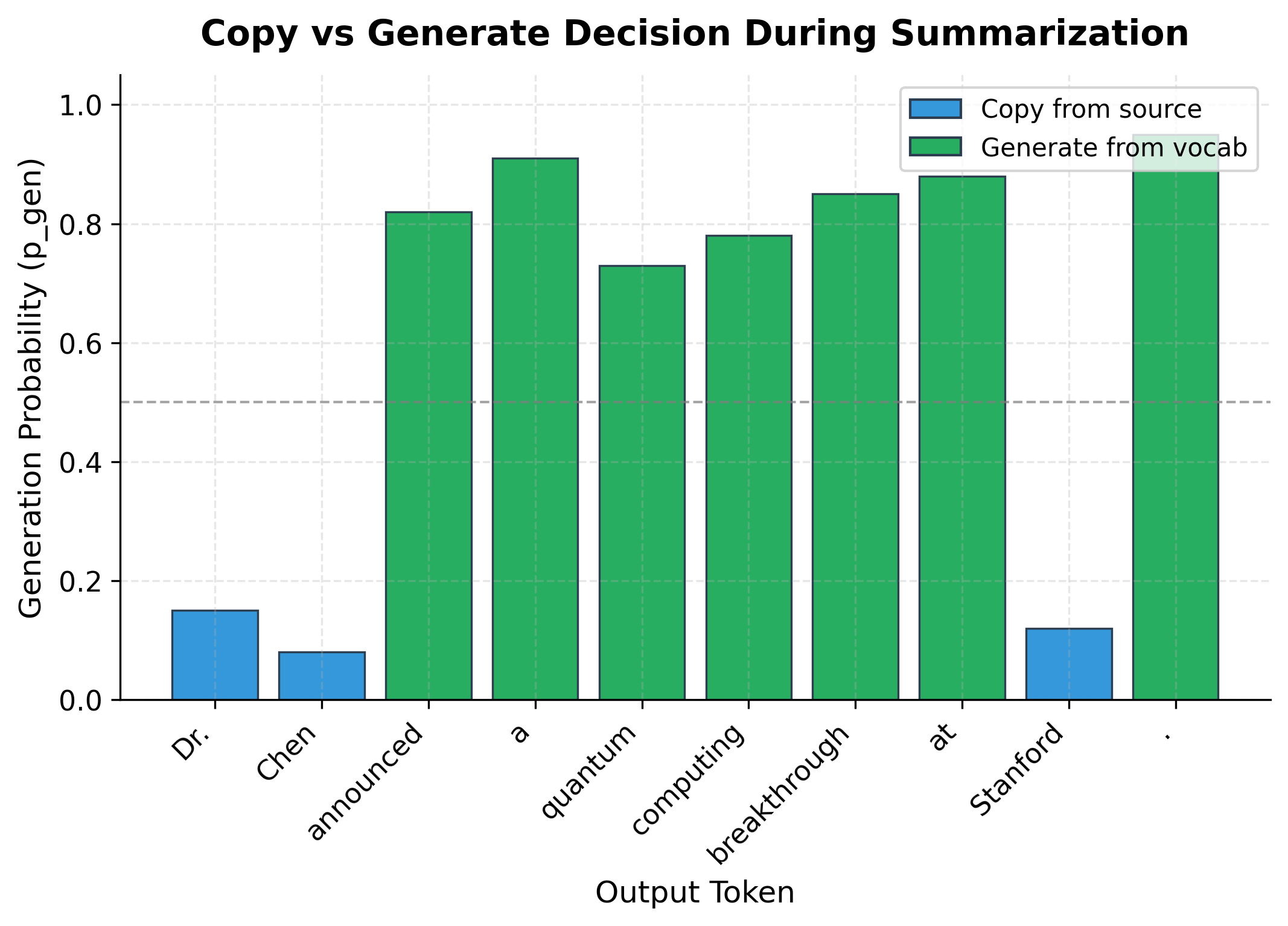
A pure pointer network can only copy from the input, but real text generation requires both copying and generating. Consider summarizing "Dr. Chen announced the results." We want to copy "Dr. Chen" (a rare name) but generate common words like "announced" and "the" from our vocabulary. How does the model decide which strategy to use at each step?

The solution introduces a soft switch between two modes: generating from vocabulary versus copying from input. Rather than making a hard binary choice, we compute a generation probability $p_{\text{gen}} \in (0, 1)$ that smoothly interpolates between the two strategies. When $p_{\text{gen}}$ is high, the model favors generation; when low, it favors copying.

What information should determine this switch? Intuitively, the decision depends on:

The context vector $c_t$ : What part of the input is the model attending to? If attention focuses on a rare word, copying makes sense.
The decoder state $s_t$ : What has the model generated so far? This captures the "momentum" of the generation process.
The previous token $x_t$ : What did we just output? After generating "Dr.", we likely want to copy the following name.

We combine these three signals through a linear combination, then squash the result to $(0, 1)$ using the sigmoid function:

p_{\text{gen}} = \sigma(w_c^T c_t + w_s^T s_t + w_x^T x_t + b)

where:

$p_{\text{gen}}$ : the probability of generating from the vocabulary (vs. copying from input)
$\sigma(\cdot)$ : the sigmoid function, $\sigma(z) = 1/(1 + e^{-z})$ , which maps any real number to the range $(0, 1)$
$c_t$ : the context vector from attention at decoder step $t$
$s_t$ : the decoder hidden state at step $t$
$x_t$ : the decoder input embedding at step $t$ (typically the previous output token)
$w_c, w_s, w_x$ : learnable weight vectors that determine how much each input contributes to the decision
$b$ : a learnable bias term that shifts the default behavior toward generating or copying

The model learns the weights $w_c, w_s, w_x$ during training. It discovers patterns like "when the context vector indicates a rare word and the decoder state suggests we're in the middle of a named entity, favor copying." These patterns emerge from the data without explicit programming.

In[8]:

Code

class CopySwitch(nn.Module):
    """
    Computes the probability of generating vs copying.
    """

    def __init__(self, hidden_dim, embed_dim):
        super().__init__()
        # Linear combination for p_gen
        self.w_context = nn.Linear(hidden_dim, 1, bias=False)
        self.w_state = nn.Linear(hidden_dim, 1, bias=False)
        self.w_input = nn.Linear(embed_dim, 1, bias=False)
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, context, decoder_state, decoder_input):
        """
        Compute generation probability.

        Args:
            context: (batch, hidden_dim) - attention context vector
            decoder_state: (batch, hidden_dim) - decoder hidden state
            decoder_input: (batch, embed_dim) - current input embedding

        Returns:
            p_gen: (batch, 1) - probability of generating from vocabulary
        """
        score = (
            self.w_context(context)
            + self.w_state(decoder_state)
            + self.w_input(decoder_input)
            + self.bias
        )
        p_gen = torch.sigmoid(score)
        return p_gen


# Example
embed_dim = 32
copy_switch = CopySwitch(hidden_dim, embed_dim)

context = torch.randn(batch_size, hidden_dim)
decoder_input = torch.randn(batch_size, embed_dim)

p_gen = copy_switch(context, decoder_state, decoder_input)

class CopySwitch(nn.Module):
    """
    Computes the probability of generating vs copying.
    """

    def __init__(self, hidden_dim, embed_dim):
        super().__init__()
        # Linear combination for p_gen
        self.w_context = nn.Linear(hidden_dim, 1, bias=False)
        self.w_state = nn.Linear(hidden_dim, 1, bias=False)
        self.w_input = nn.Linear(embed_dim, 1, bias=False)
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, context, decoder_state, decoder_input):
        """
        Compute generation probability.

        Args:
            context: (batch, hidden_dim) - attention context vector
            decoder_state: (batch, hidden_dim) - decoder hidden state
            decoder_input: (batch, embed_dim) - current input embedding

        Returns:
            p_gen: (batch, 1) - probability of generating from vocabulary
        """
        score = (
            self.w_context(context)
            + self.w_state(decoder_state)
            + self.w_input(decoder_input)
            + self.bias
        )
        p_gen = torch.sigmoid(score)
        return p_gen


# Example
embed_dim = 32
copy_switch = CopySwitch(hidden_dim, embed_dim)

context = torch.randn(batch_size, hidden_dim)
decoder_input = torch.randn(batch_size, embed_dim)

p_gen = copy_switch(context, decoder_state, decoder_input)

Out[9]:

Console

Copy Switch Output
==================================================

Generation probability p_gen:
  Batch 0: p_gen = 0.581
           p_copy = 0.419
  Batch 1: p_gen = 0.772
           p_copy = 0.228

The output reveals how the copy switch behaves: $p_{\text{gen}}$ values near 0 indicate the model prefers copying, while values near 1 indicate generation. In practice, the model learns to produce low $p_{\text{gen}}$ for rare words and names, and high $p_{\text{gen}}$ for common function words.

Mixing Generation and CopyingLink Copied

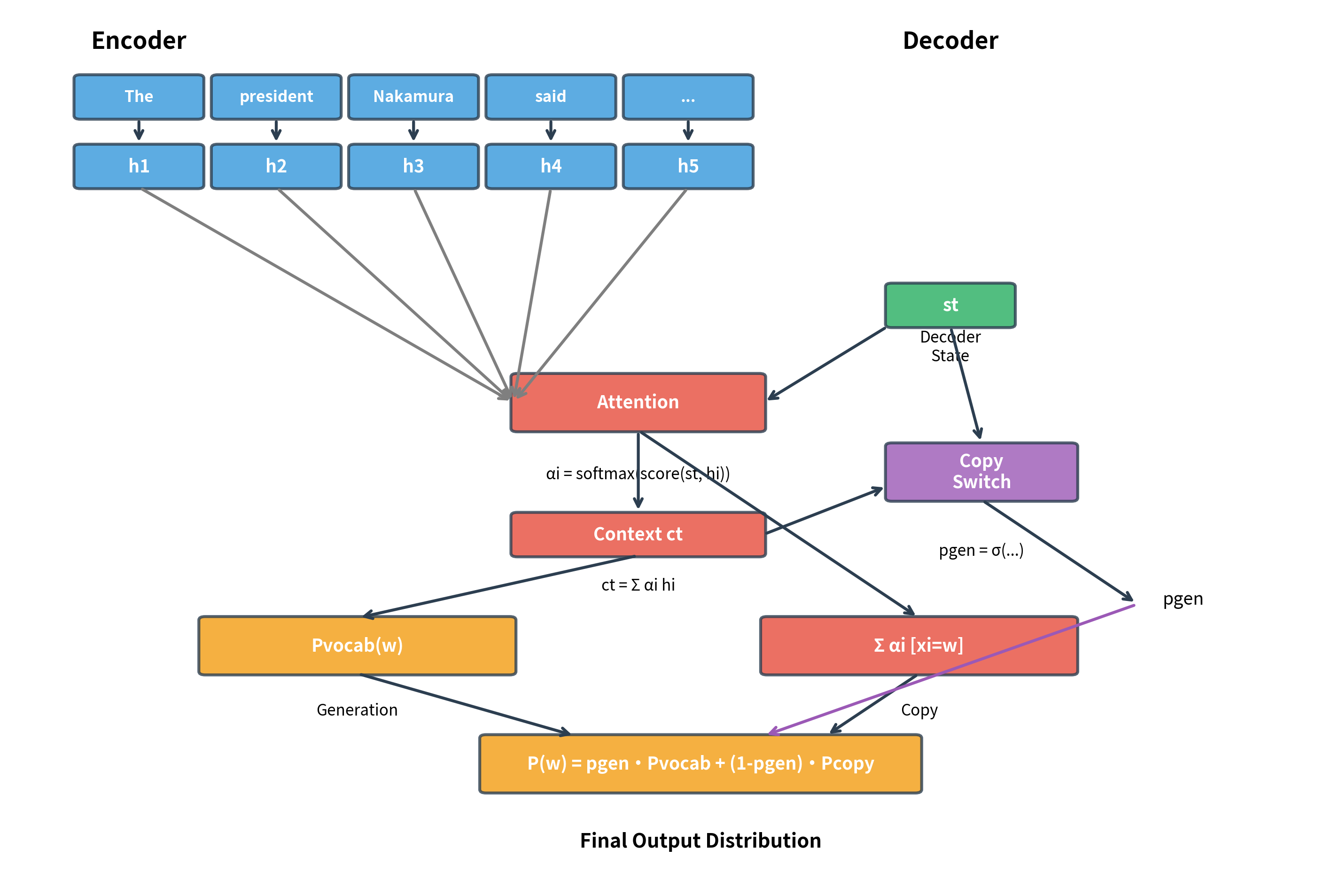
We now have two probability distributions: one over the vocabulary (from the decoder's softmax) and one over input positions (from pointer attention). We also have a switch $p_{\text{gen}}$ that tells us how much to trust each. How do we combine them into a single output distribution?

The naive approach would be to make a hard choice: either generate or copy. But this loses information and creates discontinuities that hurt gradient flow during training. Instead, we use $p_{\text{gen}}$ as a mixing coefficient that smoothly blends both distributions.

Consider a word $w$ that we might want to output. There are three cases:

$w$ is only in the vocabulary: It can only be generated, so its probability comes entirely from $P_{\text{vocab}}(w)$ , scaled by $p_{\text{gen}}$ .
$w$ is only in the input (OOV): It can only be copied, so its probability comes from the attention weights on positions containing $w$ , scaled by $(1 - p_{\text{gen}})$ .
$w$ is in both: It receives probability from both sources, which are added together.

This leads to the final probability formula:

P(w) = p_{\text{gen}} \cdot P_{\text{vocab}}(w) + (1 - p_{\text{gen}}) \cdot \sum_{i: x_i = w} a_i

where:

$P(w)$ : the final probability of outputting word $w$
$p_{\text{gen}}$ : the generation probability from the copy switch
$P_{\text{vocab}}(w)$ : the probability assigned to $w$ by the decoder's vocabulary softmax
$a_i$ : the attention weight (pointer probability) for input position $i$
$x_i$ : the token at input position $i$
$\sum_{i: x_i = w}$ : sum over all positions where the input token equals $w$

The summation $\sum_{i: x_i = w}$ deserves attention. If a word appears multiple times in the input (e.g., "the" might appear at positions 2, 7, and 15), we sum the attention weights from all those positions. This makes intuitive sense: if the model attends to any occurrence of "the" in the input, that attention contributes to the probability of outputting "the."

Let's trace through a concrete example. Suppose we're generating a summary and the input contains "the president Nakamura said." Our vocabulary includes common words but not "Nakamura." At the current step:

The vocabulary distribution assigns: $P_{\text{vocab}}(\text{said}) = 0.1$ , $P_{\text{vocab}}(\text{the}) = 0.15$
The pointer distribution assigns: $a_1 = 0.1$ (the), $a_2 = 0.3$ (president), $a_3 = 0.4$ (Nakamura), $a_4 = 0.2$ (said)
The copy switch outputs: $p_{\text{gen}} = 0.3$ (favoring copying)

For "Nakamura" (OOV, only copyable):

P(\text{Nakamura}) = 0.3 \cdot 0 + 0.7 \cdot 0.4 = 0.28

For "said" (in both vocab and input):

P(\text{said}) = 0.3 \cdot 0.1 + 0.7 \cdot 0.2 = 0.03 + 0.14 = 0.17

The OOV word "Nakamura" receives substantial probability through copying alone, while "said" gets a boost from both sources.

In[10]:

Code

def compute_final_distribution(
    p_gen,  # (batch, 1) generation probability
    vocab_dist,  # (batch, vocab_size) vocabulary distribution
    pointer_probs,  # (batch, src_len) attention/pointer distribution
    source_ids,  # (batch, src_len) token IDs in source
    vocab_size,  # int
    oov_ids=None,  # (batch, src_len) IDs for OOV tokens (optional)
):
    """
    Combine generation and copy distributions.

    For words in both vocab and source, probabilities are summed.
    For OOV words (only in source), only copy probability applies.
    """
    batch_size, src_len = source_ids.shape

    # Start with generation distribution, scaled by p_gen
    # Extended vocab includes OOV slots
    if oov_ids is not None:
        max_oov = oov_ids.max().item() + 1
        extended_size = vocab_size + max_oov
    else:
        extended_size = vocab_size

    final_dist = torch.zeros(batch_size, extended_size)
    final_dist[:, :vocab_size] = p_gen * vocab_dist

    # Add copy probabilities
    p_copy = 1 - p_gen  # (batch, 1)

    for b in range(batch_size):
        for i in range(src_len):
            token_id = source_ids[b, i].item()

            # If token is in vocab, add to that position
            if token_id < vocab_size:
                final_dist[b, token_id] += p_copy[b, 0] * pointer_probs[b, i]
            # If OOV, add to extended vocab position
            elif oov_ids is not None:
                oov_idx = oov_ids[b, i].item()
                final_dist[b, vocab_size + oov_idx] += (
                    p_copy[b, 0] * pointer_probs[b, i]
                )

    return final_dist


# Example with a small vocabulary
small_vocab = ["<unk>", "<sos>", "<eos>", "the", "said", "president"]
small_vocab_size = len(small_vocab)

# Source tokens: "the president Nakamura said"
# "Nakamura" is OOV (id = vocab_size, oov_idx = 0)
source_ids = torch.tensor([[3, 5, 6, 4]])  # the, president, <oov>, said
oov_ids = torch.tensor([[0, 0, 0, 0]])  # Only position 2 is OOV

# Simulated distributions
vocab_dist = F.softmax(torch.randn(1, small_vocab_size), dim=-1)
pointer_probs_example = torch.tensor(
    [[0.1, 0.3, 0.4, 0.2]]
)  # High attention on "Nakamura"
p_gen_example = torch.tensor([[0.3]])  # Likely to copy

final_dist = compute_final_distribution(
    p_gen_example,
    vocab_dist,
    pointer_probs_example,
    source_ids,
    small_vocab_size,
    oov_ids,
)

def compute_final_distribution(
    p_gen,  # (batch, 1) generation probability
    vocab_dist,  # (batch, vocab_size) vocabulary distribution
    pointer_probs,  # (batch, src_len) attention/pointer distribution
    source_ids,  # (batch, src_len) token IDs in source
    vocab_size,  # int
    oov_ids=None,  # (batch, src_len) IDs for OOV tokens (optional)
):
    """
    Combine generation and copy distributions.

    For words in both vocab and source, probabilities are summed.
    For OOV words (only in source), only copy probability applies.
    """
    batch_size, src_len = source_ids.shape

    # Start with generation distribution, scaled by p_gen
    # Extended vocab includes OOV slots
    if oov_ids is not None:
        max_oov = oov_ids.max().item() + 1
        extended_size = vocab_size + max_oov
    else:
        extended_size = vocab_size

    final_dist = torch.zeros(batch_size, extended_size)
    final_dist[:, :vocab_size] = p_gen * vocab_dist

    # Add copy probabilities
    p_copy = 1 - p_gen  # (batch, 1)

    for b in range(batch_size):
        for i in range(src_len):
            token_id = source_ids[b, i].item()

            # If token is in vocab, add to that position
            if token_id < vocab_size:
                final_dist[b, token_id] += p_copy[b, 0] * pointer_probs[b, i]
            # If OOV, add to extended vocab position
            elif oov_ids is not None:
                oov_idx = oov_ids[b, i].item()
                final_dist[b, vocab_size + oov_idx] += (
                    p_copy[b, 0] * pointer_probs[b, i]
                )

    return final_dist


# Example with a small vocabulary
small_vocab = ["<unk>", "<sos>", "<eos>", "the", "said", "president"]
small_vocab_size = len(small_vocab)

# Source tokens: "the president Nakamura said"
# "Nakamura" is OOV (id = vocab_size, oov_idx = 0)
source_ids = torch.tensor([[3, 5, 6, 4]])  # the, president, <oov>, said
oov_ids = torch.tensor([[0, 0, 0, 0]])  # Only position 2 is OOV

# Simulated distributions
vocab_dist = F.softmax(torch.randn(1, small_vocab_size), dim=-1)
pointer_probs_example = torch.tensor(
    [[0.1, 0.3, 0.4, 0.2]]
)  # High attention on "Nakamura"
p_gen_example = torch.tensor([[0.3]])  # Likely to copy

final_dist = compute_final_distribution(
    p_gen_example,
    vocab_dist,
    pointer_probs_example,
    source_ids,
    small_vocab_size,
    oov_ids,
)

Out[11]:

Console

Final Distribution Computation
==================================================

Source: ['the', 'president', 'Nakamura', 'said']
p_gen = 0.30 (low = prefer copying)

Pointer probabilities:
  the: 0.10
  president: 0.30
  Nakamura: 0.40
  said: 0.20

Final distribution:
  <unk>: 0.047 █
  <sos>: 0.017 
  <eos>: 0.075 ██
  the: 0.136 ████
  said: 0.186 █████
  president: 0.260 ███████
  Nakamura (OOV): 0.280 ████████

Out[12]:

Console

With $p_{\text{gen}} = 0.30$:

| Word | In Vocab | In Source | Generation | Copy | **Total** |
|:-----|:--------:|:---------:|-----------:|-----:|----------:|
| the | ✓ | ✓ | 0.066 | 0.070 | **0.136** |
| said | ✓ | ✓ | 0.046 | 0.140 | **0.186** |
| president | ✓ | ✓ | 0.050 | 0.210 | **0.260** |
| Nakamura (OOV) | — | ✓ | 0.000 | 0.280 | **0.280** |

: Final probability distribution combining generation and copy contributions. Words in both vocabulary and source (like "the" and "said") receive probability from both channels. OOV words like "Nakamura" can only be copied, receiving their entire probability from the copy mechanism. {#tbl-probability-combination}

The table reveals the mechanics of probability combination. "Nakamura" receives its entire probability from copying, since it's not in the vocabulary. "the" and "said" appear in both the source and vocabulary, so they receive contributions from both channels. With $p_{\text{gen}} = 0.30$ , the copy channel dominates, which is appropriate when the model needs to preserve specific names from the input.

The output confirms our mathematical analysis. "Nakamura," despite being out-of-vocabulary, receives the highest probability through the copy mechanism. The model can produce this word in its output even though it never appeared in training. Meanwhile, words like "said" and "the" receive probability from both generation and copying, with their contributions weighted by $p_{\text{gen}}$ .

This combination of generation and copying solves the OOV problem while preserving the model's ability to generate fluent, grammatical text. The soft switch learns to route rare words through copying and common words through generation.

The Pointer-Generator NetworkLink Copied

The pointer-generator network, introduced by See et al. (2017) for abstractive summarization, combines the ideas above into a cohesive architecture. It extends the standard attention-based seq2seq model with a copy mechanism, enabling it to both generate words from the vocabulary and copy words from the source document.

Out[13]:

Visualization

Diagram showing encoder-decoder architecture with copy mechanism, including attention, copy switch, and combined output distribution. — Architecture of the pointer-generator network. The encoder processes the source document, and the decoder generates the summary. At each step, the copy switch determines whether to generate from the vocabulary or copy from the source. The final distribution combines both possibilities, with attention weights serving as copy probabilities.

Let's implement a complete pointer-generator decoder step:

In[14]:

Code

class PointerGeneratorDecoder(nn.Module):
    """
    Single decoding step of a pointer-generator network.
    """

    def __init__(self, vocab_size, embed_dim, hidden_dim):
        super().__init__()
        self.vocab_size = vocab_size
        self.hidden_dim = hidden_dim

        # Embedding and LSTM
        self.embedding = nn.Embedding(vocab_size, embed_dim)
        self.lstm = nn.LSTMCell(embed_dim + hidden_dim, hidden_dim)

        # Attention
        self.attention = PointerAttention(hidden_dim)

        # Copy switch
        self.copy_switch = CopySwitch(hidden_dim, embed_dim)

        # Vocabulary projection
        self.vocab_proj = nn.Linear(hidden_dim * 2, vocab_size)

    def forward(
        self,
        input_token,
        prev_hidden,
        prev_cell,
        encoder_outputs,
        source_ids,
        encoder_mask=None,
    ):
        """
        Perform one decoding step.

        Args:
            input_token: (batch,) - previous output token
            prev_hidden: (batch, hidden) - previous hidden state
            prev_cell: (batch, hidden) - previous cell state
            encoder_outputs: (batch, src_len, hidden) - encoder outputs
            source_ids: (batch, src_len) - source token IDs
            encoder_mask: (batch, src_len) - valid source positions

        Returns:
            final_dist: (batch, extended_vocab) - output distribution
            hidden: (batch, hidden) - new hidden state
            cell: (batch, hidden) - new cell state
            attn_weights: (batch, src_len) - attention weights
        """
        batch_size = input_token.shape[0]

        # Embed input
        embedded = self.embedding(input_token)  # (batch, embed)

        # Compute attention over encoder outputs
        attn_weights = self.attention(
            prev_hidden, encoder_outputs, encoder_mask
        )

        # Context vector
        context = torch.bmm(attn_weights.unsqueeze(1), encoder_outputs).squeeze(
            1
        )

        # LSTM input: concatenate embedding and context
        lstm_input = torch.cat([embedded, context], dim=-1)

        # LSTM step
        hidden, cell = self.lstm(lstm_input, (prev_hidden, prev_cell))

        # Vocabulary distribution
        vocab_input = torch.cat([hidden, context], dim=-1)
        vocab_logits = self.vocab_proj(vocab_input)
        vocab_dist = F.softmax(vocab_logits, dim=-1)

        # Copy probability
        p_gen = self.copy_switch(context, hidden, embedded)

        # Combine distributions
        final_dist = self._combine_distributions(
            p_gen, vocab_dist, attn_weights, source_ids
        )

        return final_dist, hidden, cell, attn_weights

    def _combine_distributions(
        self, p_gen, vocab_dist, attn_weights, source_ids
    ):
        """Combine generation and copy distributions."""
        batch_size, src_len = source_ids.shape

        # For simplicity, assume no OOV (would need extended vocab otherwise)
        final_dist = p_gen * vocab_dist

        # Add copy probabilities
        p_copy = 1 - p_gen

        # Use scatter_add for efficiency
        copy_dist = torch.zeros_like(vocab_dist)
        copy_dist.scatter_add_(1, source_ids, attn_weights * p_copy)

        final_dist = final_dist + copy_dist

        return final_dist


# Test the decoder
vocab_size = 1000
embed_dim = 64
hidden_dim = 128
batch_size = 2
src_len = 10

decoder = PointerGeneratorDecoder(vocab_size, embed_dim, hidden_dim)

# Dummy inputs
input_token = torch.randint(0, vocab_size, (batch_size,))
prev_hidden = torch.zeros(batch_size, hidden_dim)
prev_cell = torch.zeros(batch_size, hidden_dim)
encoder_outputs = torch.randn(batch_size, src_len, hidden_dim)
source_ids = torch.randint(0, vocab_size, (batch_size, src_len))

final_dist, hidden, cell, attn = decoder(
    input_token, prev_hidden, prev_cell, encoder_outputs, source_ids
)

class PointerGeneratorDecoder(nn.Module):
    """
    Single decoding step of a pointer-generator network.
    """

    def __init__(self, vocab_size, embed_dim, hidden_dim):
        super().__init__()
        self.vocab_size = vocab_size
        self.hidden_dim = hidden_dim

        # Embedding and LSTM
        self.embedding = nn.Embedding(vocab_size, embed_dim)
        self.lstm = nn.LSTMCell(embed_dim + hidden_dim, hidden_dim)

        # Attention
        self.attention = PointerAttention(hidden_dim)

        # Copy switch
        self.copy_switch = CopySwitch(hidden_dim, embed_dim)

        # Vocabulary projection
        self.vocab_proj = nn.Linear(hidden_dim * 2, vocab_size)

    def forward(
        self,
        input_token,
        prev_hidden,
        prev_cell,
        encoder_outputs,
        source_ids,
        encoder_mask=None,
    ):
        """
        Perform one decoding step.

        Args:
            input_token: (batch,) - previous output token
            prev_hidden: (batch, hidden) - previous hidden state
            prev_cell: (batch, hidden) - previous cell state
            encoder_outputs: (batch, src_len, hidden) - encoder outputs
            source_ids: (batch, src_len) - source token IDs
            encoder_mask: (batch, src_len) - valid source positions

        Returns:
            final_dist: (batch, extended_vocab) - output distribution
            hidden: (batch, hidden) - new hidden state
            cell: (batch, hidden) - new cell state
            attn_weights: (batch, src_len) - attention weights
        """
        batch_size = input_token.shape[0]

        # Embed input
        embedded = self.embedding(input_token)  # (batch, embed)

        # Compute attention over encoder outputs
        attn_weights = self.attention(
            prev_hidden, encoder_outputs, encoder_mask
        )

        # Context vector
        context = torch.bmm(attn_weights.unsqueeze(1), encoder_outputs).squeeze(
            1
        )

        # LSTM input: concatenate embedding and context
        lstm_input = torch.cat([embedded, context], dim=-1)

        # LSTM step
        hidden, cell = self.lstm(lstm_input, (prev_hidden, prev_cell))

        # Vocabulary distribution
        vocab_input = torch.cat([hidden, context], dim=-1)
        vocab_logits = self.vocab_proj(vocab_input)
        vocab_dist = F.softmax(vocab_logits, dim=-1)

        # Copy probability
        p_gen = self.copy_switch(context, hidden, embedded)

        # Combine distributions
        final_dist = self._combine_distributions(
            p_gen, vocab_dist, attn_weights, source_ids
        )

        return final_dist, hidden, cell, attn_weights

    def _combine_distributions(
        self, p_gen, vocab_dist, attn_weights, source_ids
    ):
        """Combine generation and copy distributions."""
        batch_size, src_len = source_ids.shape

        # For simplicity, assume no OOV (would need extended vocab otherwise)
        final_dist = p_gen * vocab_dist

        # Add copy probabilities
        p_copy = 1 - p_gen

        # Use scatter_add for efficiency
        copy_dist = torch.zeros_like(vocab_dist)
        copy_dist.scatter_add_(1, source_ids, attn_weights * p_copy)

        final_dist = final_dist + copy_dist

        return final_dist


# Test the decoder
vocab_size = 1000
embed_dim = 64
hidden_dim = 128
batch_size = 2
src_len = 10

decoder = PointerGeneratorDecoder(vocab_size, embed_dim, hidden_dim)

# Dummy inputs
input_token = torch.randint(0, vocab_size, (batch_size,))
prev_hidden = torch.zeros(batch_size, hidden_dim)
prev_cell = torch.zeros(batch_size, hidden_dim)
encoder_outputs = torch.randn(batch_size, src_len, hidden_dim)
source_ids = torch.randint(0, vocab_size, (batch_size, src_len))

final_dist, hidden, cell, attn = decoder(
    input_token, prev_hidden, prev_cell, encoder_outputs, source_ids
)

Out[15]:

Console

Pointer-Generator Decoder Output
==================================================

Output distribution shape: torch.Size([2, 1000])
Hidden state shape: torch.Size([2, 128])
Attention weights shape: torch.Size([2, 10])

Top 5 predicted tokens (batch 0):
  Token 135: 0.1007
  Token 147: 0.0951
  Token 521: 0.0901
  Token 404: 0.0866
  Token 118: 0.0744

Distribution sum: 1.0000

The output distribution sums to 1.0, confirming it's a valid probability distribution. The decoder produces probabilities over all tokens in the vocabulary, and the top predictions show which tokens are most likely at this step. In practice, these probabilities would be used either for greedy decoding (selecting the argmax) or for beam search (maintaining multiple hypotheses).

Copy Mechanism for SummarizationLink Copied

Abstractive summarization is the canonical application for copy mechanisms. Summaries must preserve key facts, names, and numbers from the source document while also rephrasing and condensing the content. The pointer-generator architecture excels at this balance.

In[16]:

Code

# Simulate summarization scenario
source_document = """
Dr. Sarah Chen, a researcher at Stanford University, announced a breakthrough 
in quantum computing. The discovery, published in Nature on March 15, could 
reduce error rates by 47 percent. Chen's team worked with IBM and Google 
on the three-year project.
"""

# Words that MUST be copied (rare/specific)
must_copy = [
    "Sarah",
    "Chen",
    "Stanford",
    "Nature",
    "March",
    "15",
    "47",
    "IBM",
    "Google",
]

# Words that could be generated (common)
can_generate = [
    "researcher",
    "announced",
    "breakthrough",
    "discovery",
    "published",
    "reduce",
    "team",
    "project",
]

# Build a simple vocabulary (missing the rare words)
simple_vocab = [
    "<pad>",
    "<unk>",
    "<sos>",
    "<eos>",
    "the",
    "a",
    "in",
    "at",
    "on",
    "by",
    "and",
    "to",
    "of",
    "that",
    "which",
    "percent",
    "researcher",
    "announced",
    "breakthrough",
    "discovery",
    "published",
    "reduce",
    "team",
    "project",
    "university",
    "computing",
    "quantum",
    "error",
    "rates",
    "year",
    "three",
]

# Simulate summarization scenario
source_document = """
Dr. Sarah Chen, a researcher at Stanford University, announced a breakthrough 
in quantum computing. The discovery, published in Nature on March 15, could 
reduce error rates by 47 percent. Chen's team worked with IBM and Google 
on the three-year project.
"""

# Words that MUST be copied (rare/specific)
must_copy = [
    "Sarah",
    "Chen",
    "Stanford",
    "Nature",
    "March",
    "15",
    "47",
    "IBM",
    "Google",
]

# Words that could be generated (common)
can_generate = [
    "researcher",
    "announced",
    "breakthrough",
    "discovery",
    "published",
    "reduce",
    "team",
    "project",
]

# Build a simple vocabulary (missing the rare words)
simple_vocab = [
    "<pad>",
    "<unk>",
    "<sos>",
    "<eos>",
    "the",
    "a",
    "in",
    "at",
    "on",
    "by",
    "and",
    "to",
    "of",
    "that",
    "which",
    "percent",
    "researcher",
    "announced",
    "breakthrough",
    "discovery",
    "published",
    "reduce",
    "team",
    "project",
    "university",
    "computing",
    "quantum",
    "error",
    "rates",
    "year",
    "three",
]

Out[17]:

Console

Summarization Vocabulary Analysis
==================================================

Source document excerpt:
  '
Dr. Sarah Chen, a researcher at Stanford University, announced a breakthrough 
in quantum computing...'

Critical words that must be copied:
  Sarah: ✗ OOV - needs copy
  Chen: ✗ OOV - needs copy
  Stanford: ✗ OOV - needs copy
  Nature: ✗ OOV - needs copy
  March: ✗ OOV - needs copy
  15: ✗ OOV - needs copy
  47: ✗ OOV - needs copy
  IBM: ✗ OOV - needs copy
  Google: ✗ OOV - needs copy

Common words that can be generated:
  researcher: ✓ in vocab
  announced: ✓ in vocab
  breakthrough: ✓ in vocab
  discovery: ✓ in vocab

Let's trace through how the model would generate a summary:

In[18]:

Code

# Simulated generation trace
generation_trace = [
    {"token": "Dr.", "source": "copy", "p_gen": 0.15, "attn_peak": "Dr."},
    {"token": "Chen", "source": "copy", "p_gen": 0.08, "attn_peak": "Chen"},
    {
        "token": "announced",
        "source": "generate",
        "p_gen": 0.82,
        "attn_peak": None,
    },
    {"token": "a", "source": "generate", "p_gen": 0.91, "attn_peak": None},
    {
        "token": "quantum",
        "source": "generate",
        "p_gen": 0.73,
        "attn_peak": None,
    },
    {
        "token": "computing",
        "source": "generate",
        "p_gen": 0.78,
        "attn_peak": None,
    },
    {
        "token": "breakthrough",
        "source": "generate",
        "p_gen": 0.85,
        "attn_peak": None,
    },
    {"token": "at", "source": "generate", "p_gen": 0.88, "attn_peak": None},
    {
        "token": "Stanford",
        "source": "copy",
        "p_gen": 0.12,
        "attn_peak": "Stanford",
    },
    {"token": ".", "source": "generate", "p_gen": 0.95, "attn_peak": None},
]

# Simulated generation trace
generation_trace = [
    {"token": "Dr.", "source": "copy", "p_gen": 0.15, "attn_peak": "Dr."},
    {"token": "Chen", "source": "copy", "p_gen": 0.08, "attn_peak": "Chen"},
    {
        "token": "announced",
        "source": "generate",
        "p_gen": 0.82,
        "attn_peak": None,
    },
    {"token": "a", "source": "generate", "p_gen": 0.91, "attn_peak": None},
    {
        "token": "quantum",
        "source": "generate",
        "p_gen": 0.73,
        "attn_peak": None,
    },
    {
        "token": "computing",
        "source": "generate",
        "p_gen": 0.78,
        "attn_peak": None,
    },
    {
        "token": "breakthrough",
        "source": "generate",
        "p_gen": 0.85,
        "attn_peak": None,
    },
    {"token": "at", "source": "generate", "p_gen": 0.88, "attn_peak": None},
    {
        "token": "Stanford",
        "source": "copy",
        "p_gen": 0.12,
        "attn_peak": "Stanford",
    },
    {"token": ".", "source": "generate", "p_gen": 0.95, "attn_peak": None},
]

Out[19]:

Console

Generation Trace
============================================================

Generating summary: 'Dr. Chen announced a quantum computing breakthrough at Stanford.'

Token           Source     p_gen    Attention Peak
-------------------------------------------------------
Dr.             copy       0.15     Dr.
Chen            copy       0.08     Chen
announced       generate   0.82     -
a               generate   0.91     -
quantum         generate   0.73     -
computing       generate   0.78     -
breakthrough    generate   0.85     -
at              generate   0.88     -
Stanford        copy       0.12     Stanford
.               generate   0.95     -

Note: Low p_gen indicates copying; high p_gen indicates generation

Out[20]:

Visualization

Bar chart showing p_gen values for each token in generated summary, colored by copy vs generate decision. — Generation probability (p_gen) during summary generation. Low values indicate copying from the source (shown in blue), while high values indicate generation from vocabulary (shown in green). Names and rare words trigger copying, while common words are generated.

Handling Out-of-Vocabulary WordsLink Copied

The copy mechanism's most important contribution is handling out-of-vocabulary (OOV) words. Without copying, rare words would be replaced with <unk> tokens, destroying factual accuracy. With copying, these words can appear in the output even if they never occurred in training.

The implementation requires extending the vocabulary dynamically for each input:

In[21]:

Code

class OOVHandler:
    """
    Handles out-of-vocabulary words for copy mechanism.
    """

    def __init__(self, vocab):
        self.vocab = vocab
        self.word_to_idx = {word: i for i, word in enumerate(vocab)}
        self.vocab_size = len(vocab)

    def process_source(self, source_tokens):
        """
        Convert source tokens to IDs, tracking OOV words.

        Returns:
            source_ids: List of token IDs (OOV words get extended IDs)
            oov_words: List of OOV words encountered
            extended_vocab: Original vocab + OOV words
        """
        source_ids = []
        oov_words = []
        oov_to_idx = {}

        for token in source_tokens:
            if token in self.word_to_idx:
                source_ids.append(self.word_to_idx[token])
            else:
                # OOV word
                if token not in oov_to_idx:
                    oov_to_idx[token] = len(oov_words)
                    oov_words.append(token)
                # Extended ID = vocab_size + oov_index
                source_ids.append(self.vocab_size + oov_to_idx[token])

        extended_vocab = self.vocab + oov_words
        return source_ids, oov_words, extended_vocab

    def decode_output(self, output_ids, oov_words):
        """
        Convert output IDs back to tokens, using OOV words when needed.
        """
        output_tokens = []
        for idx in output_ids:
            if idx < self.vocab_size:
                output_tokens.append(self.vocab[idx])
            else:
                oov_idx = idx - self.vocab_size
                if oov_idx < len(oov_words):
                    output_tokens.append(oov_words[oov_idx])
                else:
                    output_tokens.append("<unk>")
        return output_tokens


# Example
base_vocab = [
    "<pad>",
    "<unk>",
    "<sos>",
    "<eos>",
    "the",
    "said",
    "at",
    "university",
]
handler = OOVHandler(base_vocab)

source = [
    "Dr.",
    "Chen",
    "said",
    "the",
    "discovery",
    "at",
    "Stanford",
    "university",
]
source_ids, oov_words, extended_vocab = handler.process_source(source)

class OOVHandler:
    """
    Handles out-of-vocabulary words for copy mechanism.
    """

    def __init__(self, vocab):
        self.vocab = vocab
        self.word_to_idx = {word: i for i, word in enumerate(vocab)}
        self.vocab_size = len(vocab)

    def process_source(self, source_tokens):
        """
        Convert source tokens to IDs, tracking OOV words.

        Returns:
            source_ids: List of token IDs (OOV words get extended IDs)
            oov_words: List of OOV words encountered
            extended_vocab: Original vocab + OOV words
        """
        source_ids = []
        oov_words = []
        oov_to_idx = {}

        for token in source_tokens:
            if token in self.word_to_idx:
                source_ids.append(self.word_to_idx[token])
            else:
                # OOV word
                if token not in oov_to_idx:
                    oov_to_idx[token] = len(oov_words)
                    oov_words.append(token)
                # Extended ID = vocab_size + oov_index
                source_ids.append(self.vocab_size + oov_to_idx[token])

        extended_vocab = self.vocab + oov_words
        return source_ids, oov_words, extended_vocab

    def decode_output(self, output_ids, oov_words):
        """
        Convert output IDs back to tokens, using OOV words when needed.
        """
        output_tokens = []
        for idx in output_ids:
            if idx < self.vocab_size:
                output_tokens.append(self.vocab[idx])
            else:
                oov_idx = idx - self.vocab_size
                if oov_idx < len(oov_words):
                    output_tokens.append(oov_words[oov_idx])
                else:
                    output_tokens.append("<unk>")
        return output_tokens


# Example
base_vocab = [
    "<pad>",
    "<unk>",
    "<sos>",
    "<eos>",
    "the",
    "said",
    "at",
    "university",
]
handler = OOVHandler(base_vocab)

source = [
    "Dr.",
    "Chen",
    "said",
    "the",
    "discovery",
    "at",
    "Stanford",
    "university",
]
source_ids, oov_words, extended_vocab = handler.process_source(source)

Out[22]:

Console

OOV Handling
==================================================

Base vocabulary size: 8
Base vocab: ['<pad>', '<unk>', '<sos>', '<eos>', 'the', 'said', 'at', 'university']

Source: ['Dr.', 'Chen', 'said', 'the', 'discovery', 'at', 'Stanford', 'university']

Processed source IDs: [8, 9, 5, 4, 10, 6, 11, 7]
OOV words found: ['Dr.', 'Chen', 'discovery', 'Stanford']

Extended vocabulary: ['<pad>', '<unk>', '<sos>', '<eos>', 'the', 'said', 'at', 'university', 'Dr.', 'Chen', 'discovery', 'Stanford']

Token mapping:
  Dr. -> 8 (OOV, extended)
  Chen -> 9 (OOV, extended)
  said -> 5 (in vocab)
  the -> 4 (in vocab)
  discovery -> 10 (OOV, extended)
  at -> 6 (in vocab)
  Stanford -> 11 (OOV, extended)
  university -> 7 (in vocab)

The OOV handler assigns extended vocabulary IDs to words not in the base vocabulary. "Dr.", "Chen", "discovery", and "Stanford" receive IDs starting from the base vocabulary size (8), allowing the copy mechanism to produce these tokens even though they weren't in the original vocabulary. This dynamic vocabulary extension is computed per-input, so different source documents can have different OOV words.

During training, we need to handle the case where target tokens are OOV:

In[23]:

Code

def compute_loss_with_oov(final_dist, target_ids, vocab_size):
    """
    Compute cross-entropy loss, handling OOV targets.

    If target is OOV but copyable from source, loss is computed
    against the extended distribution. If target is truly unknown,
    it's mapped to <unk>.
    """
    batch_size = target_ids.shape[0]
    extended_size = final_dist.shape[1]

    # Clamp target IDs to valid range
    # OOV targets beyond extended vocab map to <unk> (index 1)
    valid_targets = target_ids.clone()
    valid_targets[valid_targets >= extended_size] = 1  # <unk>

    # Gather probabilities for target tokens
    target_probs = final_dist.gather(1, valid_targets.unsqueeze(1)).squeeze(1)

    # Negative log likelihood
    loss = -torch.log(target_probs + 1e-12)

    return loss.mean()


# Example
target_ids = torch.tensor([8, 9, 5])  # "Dr.", "Chen", "said"
# "Dr." and "Chen" are OOV (ids 8, 9), "said" is in vocab (id 5)

# Simulated final distribution (extended vocab)
final_dist = torch.zeros(3, 12)  # batch=3, extended_vocab=12
final_dist[0, 8] = 0.7  # High prob for "Dr." (copied)
final_dist[1, 9] = 0.6  # High prob for "Chen" (copied)
final_dist[2, 5] = 0.8  # High prob for "said" (generated)

loss = compute_loss_with_oov(final_dist, target_ids, len(base_vocab))

def compute_loss_with_oov(final_dist, target_ids, vocab_size):
    """
    Compute cross-entropy loss, handling OOV targets.

    If target is OOV but copyable from source, loss is computed
    against the extended distribution. If target is truly unknown,
    it's mapped to <unk>.
    """
    batch_size = target_ids.shape[0]
    extended_size = final_dist.shape[1]

    # Clamp target IDs to valid range
    # OOV targets beyond extended vocab map to <unk> (index 1)
    valid_targets = target_ids.clone()
    valid_targets[valid_targets >= extended_size] = 1  # <unk>

    # Gather probabilities for target tokens
    target_probs = final_dist.gather(1, valid_targets.unsqueeze(1)).squeeze(1)

    # Negative log likelihood
    loss = -torch.log(target_probs + 1e-12)

    return loss.mean()


# Example
target_ids = torch.tensor([8, 9, 5])  # "Dr.", "Chen", "said"
# "Dr." and "Chen" are OOV (ids 8, 9), "said" is in vocab (id 5)

# Simulated final distribution (extended vocab)
final_dist = torch.zeros(3, 12)  # batch=3, extended_vocab=12
final_dist[0, 8] = 0.7  # High prob for "Dr." (copied)
final_dist[1, 9] = 0.6  # High prob for "Chen" (copied)
final_dist[2, 5] = 0.8  # High prob for "said" (generated)

loss = compute_loss_with_oov(final_dist, target_ids, len(base_vocab))

Out[24]:

Console

Loss Computation with OOV
==================================================

Target tokens: ['Dr.', 'Chen', 'said']
Target IDs: [8, 9, 5]
Base vocab size: 8

Probabilities assigned to targets:
  P('Dr.') = 0.70 (OOV, copied)
  P('Chen') = 0.60 (OOV, copied)
  P('said') = 0.80 (in vocab, generated)

Loss: 0.3635

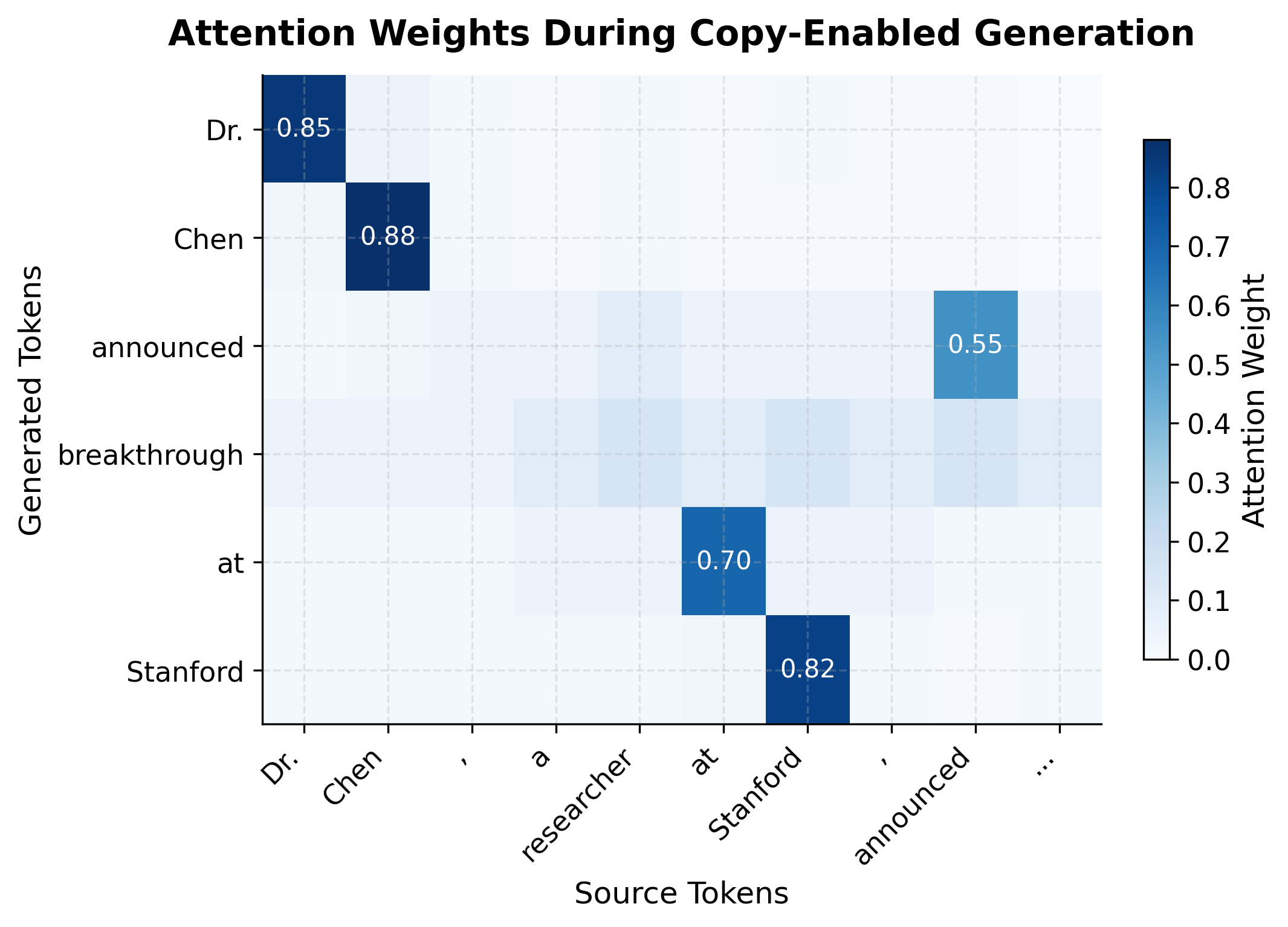
Attention Visualization for CopyLink Copied

Visualizing attention patterns reveals when and what the model copies. High attention on specific source positions often indicates copying, especially when $p_{\text{gen}}$ is low.

Out[25]:

Visualization

Heatmap showing attention weights between generated summary tokens and source document tokens. — Attention heatmap during summarization with copy mechanism. Each row shows attention weights when generating a summary token. High attention (darker cells) on source tokens like 'Chen' and 'Stanford' indicates copying, while diffuse attention during generation of common words like 'announced' shows the model drawing context from multiple positions.

Coverage MechanismLink Copied

One issue with attention-based models is repetition: the model may attend to the same source positions multiple times, generating repetitive output. The coverage mechanism addresses this by tracking which source positions have already been attended to.

Coverage Mechanism

Coverage maintains a running sum of attention distributions from all previous decoder steps. This coverage vector is used to penalize re-attending to already-covered positions, reducing repetition in the output.

The coverage vector $c_t$ at decoder step $t$ accumulates all previous attention distributions:

c_t = \sum_{t'=0}^{t-1} a_{t'}

where:

$c_t$ : the coverage vector at step $t$ , with one value per source position
$a_{t'}$ : the attention distribution at previous step $t'$
The sum runs over all previous decoder steps from $0$ to $t-1$

Each element $c_{t,i}$ represents how much total attention has been paid to source position $i$ so far. High values indicate positions that have been heavily attended; low values indicate under-attended positions.

This coverage vector is incorporated into the attention computation, encouraging the model to attend to positions with low coverage. Additionally, a coverage loss explicitly penalizes re-attending to already-covered positions:

\text{covloss}_t = \sum_i \min(a_{t,i}, c_{t,i})

where:

$\text{covloss}_t$ : the coverage loss at step $t$
$a_{t,i}$ : the current attention weight on source position $i$
$c_{t,i}$ : the accumulated coverage at position $i$
$\min(\cdot, \cdot)$ : takes the element-wise minimum

The intuition behind the $\min$ function: the loss is only incurred when both the current attention $a_{t,i}$ and the past coverage $c_{t,i}$ are high for the same position. If either is low, the contribution to the loss is small. This allows the model to attend to new positions freely while penalizing redundant attention to already-covered content.

In[26]:

Code

class CoverageAttention(nn.Module):
    """
    Attention with coverage mechanism to reduce repetition.
    """

    def __init__(self, hidden_dim):
        super().__init__()
        self.hidden_dim = hidden_dim

        # Standard attention parameters
        self.W_encoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_decoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_coverage = nn.Linear(1, hidden_dim, bias=False)
        self.v = nn.Linear(hidden_dim, 1, bias=False)

    def forward(self, decoder_state, encoder_outputs, coverage, mask=None):
        """
        Compute attention with coverage.

        Args:
            decoder_state: (batch, hidden)
            encoder_outputs: (batch, seq_len, hidden)
            coverage: (batch, seq_len) - sum of previous attention weights
            mask: (batch, seq_len)

        Returns:
            attn_weights: (batch, seq_len)
            coverage_loss: scalar
        """
        batch_size, seq_len, _ = encoder_outputs.shape

        # Project inputs
        encoder_proj = self.W_encoder(encoder_outputs)  # (batch, seq, hidden)
        decoder_proj = self.W_decoder(decoder_state).unsqueeze(
            1
        )  # (batch, 1, hidden)
        coverage_proj = self.W_coverage(
            coverage.unsqueeze(-1)
        )  # (batch, seq, hidden)

        # Compute scores with coverage
        scores = self.v(torch.tanh(encoder_proj + decoder_proj + coverage_proj))
        scores = scores.squeeze(-1)  # (batch, seq_len)

        if mask is not None:
            scores = scores.masked_fill(~mask, float("-inf"))

        attn_weights = F.softmax(scores, dim=-1)

        # Coverage loss: penalize re-attending
        coverage_loss = torch.sum(
            torch.min(attn_weights, coverage), dim=-1
        ).mean()

        return attn_weights, coverage_loss


# Example
# Use dimensions from PointerGeneratorDecoder
cov_hidden_dim = 128
cov_batch_size = 2
cov_src_len = 10

coverage_attn = CoverageAttention(cov_hidden_dim)

# Create matching tensors
cov_decoder_state = torch.randn(cov_batch_size, cov_hidden_dim)
cov_encoder_outputs = torch.randn(cov_batch_size, cov_src_len, cov_hidden_dim)

# Simulated coverage from previous steps
coverage = torch.tensor([[0.0, 0.3, 0.5, 0.1, 0.1, 0.0, 0.0, 0.0, 0.0, 0.0]])
coverage = coverage.expand(cov_batch_size, -1)

attn_weights, cov_loss = coverage_attn(
    cov_decoder_state,
    cov_encoder_outputs,
    coverage,
)

class CoverageAttention(nn.Module):
    """
    Attention with coverage mechanism to reduce repetition.
    """

    def __init__(self, hidden_dim):
        super().__init__()
        self.hidden_dim = hidden_dim

        # Standard attention parameters
        self.W_encoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_decoder = nn.Linear(hidden_dim, hidden_dim, bias=False)
        self.W_coverage = nn.Linear(1, hidden_dim, bias=False)
        self.v = nn.Linear(hidden_dim, 1, bias=False)

    def forward(self, decoder_state, encoder_outputs, coverage, mask=None):
        """
        Compute attention with coverage.

        Args:
            decoder_state: (batch, hidden)
            encoder_outputs: (batch, seq_len, hidden)
            coverage: (batch, seq_len) - sum of previous attention weights
            mask: (batch, seq_len)

        Returns:
            attn_weights: (batch, seq_len)
            coverage_loss: scalar
        """
        batch_size, seq_len, _ = encoder_outputs.shape

        # Project inputs
        encoder_proj = self.W_encoder(encoder_outputs)  # (batch, seq, hidden)
        decoder_proj = self.W_decoder(decoder_state).unsqueeze(
            1
        )  # (batch, 1, hidden)
        coverage_proj = self.W_coverage(
            coverage.unsqueeze(-1)
        )  # (batch, seq, hidden)

        # Compute scores with coverage
        scores = self.v(torch.tanh(encoder_proj + decoder_proj + coverage_proj))
        scores = scores.squeeze(-1)  # (batch, seq_len)

        if mask is not None:
            scores = scores.masked_fill(~mask, float("-inf"))

        attn_weights = F.softmax(scores, dim=-1)

        # Coverage loss: penalize re-attending
        coverage_loss = torch.sum(
            torch.min(attn_weights, coverage), dim=-1
        ).mean()

        return attn_weights, coverage_loss


# Example
# Use dimensions from PointerGeneratorDecoder
cov_hidden_dim = 128
cov_batch_size = 2
cov_src_len = 10

coverage_attn = CoverageAttention(cov_hidden_dim)

# Create matching tensors
cov_decoder_state = torch.randn(cov_batch_size, cov_hidden_dim)
cov_encoder_outputs = torch.randn(cov_batch_size, cov_src_len, cov_hidden_dim)

# Simulated coverage from previous steps
coverage = torch.tensor([[0.0, 0.3, 0.5, 0.1, 0.1, 0.0, 0.0, 0.0, 0.0, 0.0]])
coverage = coverage.expand(cov_batch_size, -1)

attn_weights, cov_loss = coverage_attn(
    cov_decoder_state,
    cov_encoder_outputs,
    coverage,
)

Out[27]:

Console

Coverage Mechanism
==================================================

Previous coverage (positions already attended):
  Position 1: 0.30 ██████
  Position 2: 0.50 ██████████
  Position 3: 0.10 ██
  Position 4: 0.10 ██

New attention weights:
  Position 0: 0.106 ██
  Position 1: 0.104 ██
  Position 2: 0.073 █
  Position 3: 0.103 ██
  Position 4: 0.078 █
  Position 5: 0.135 ██
  Position 6: 0.078 █
  Position 7: 0.122 ██
  Position 8: 0.107 ██
  Position 9: 0.094 █

Coverage loss: 0.3610
(Lower is better - means less re-attending to covered positions)

Out[28]:

Visualization

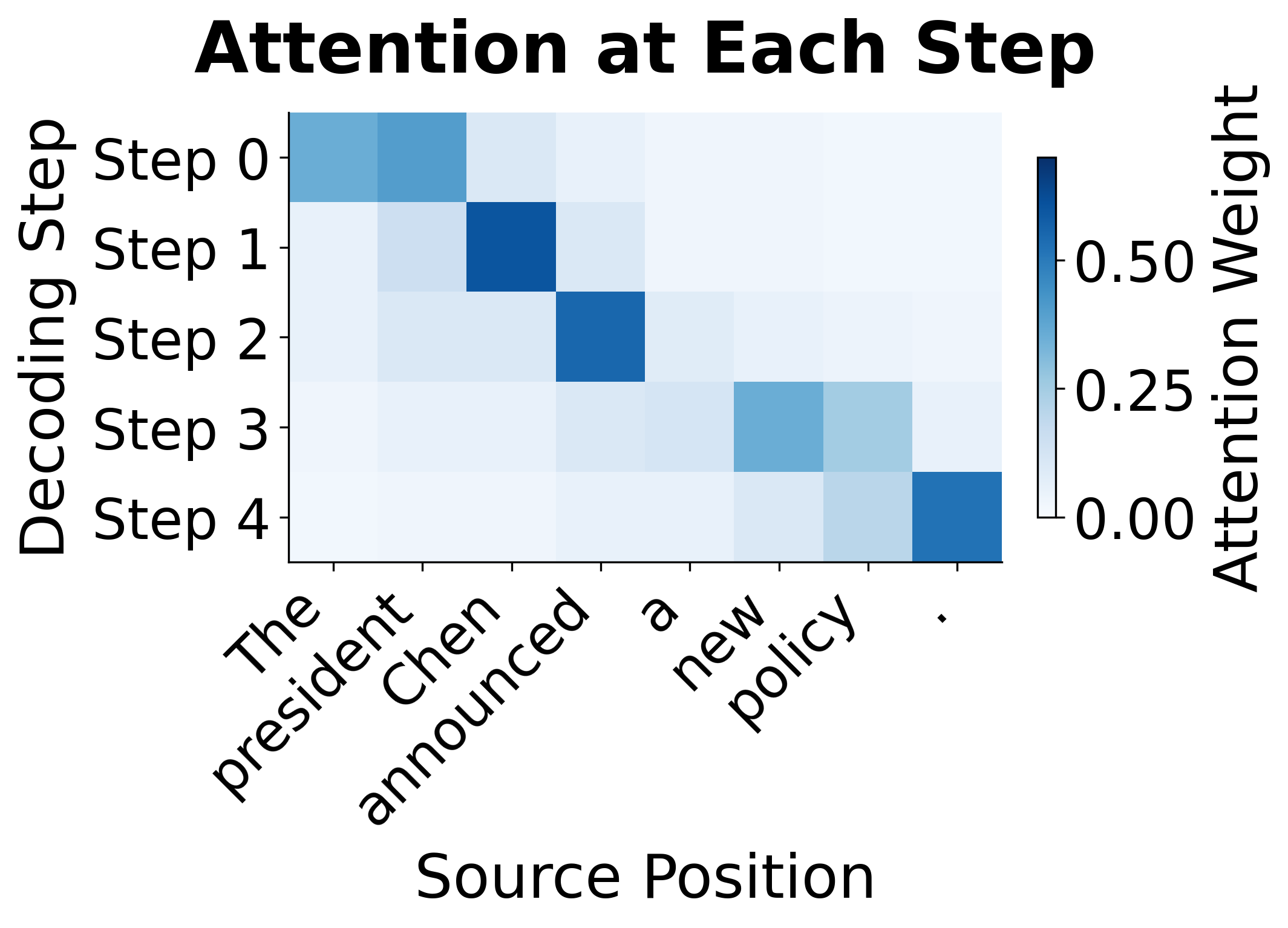
Heatmap showing attention weights at each decoding step over source tokens. — Attention distributions at each decoding step. Each row shows where the model attends when generating that step's output. Early steps focus on 'The president' and 'Chen', while later steps shift to 'announced', 'new policy', and the period.

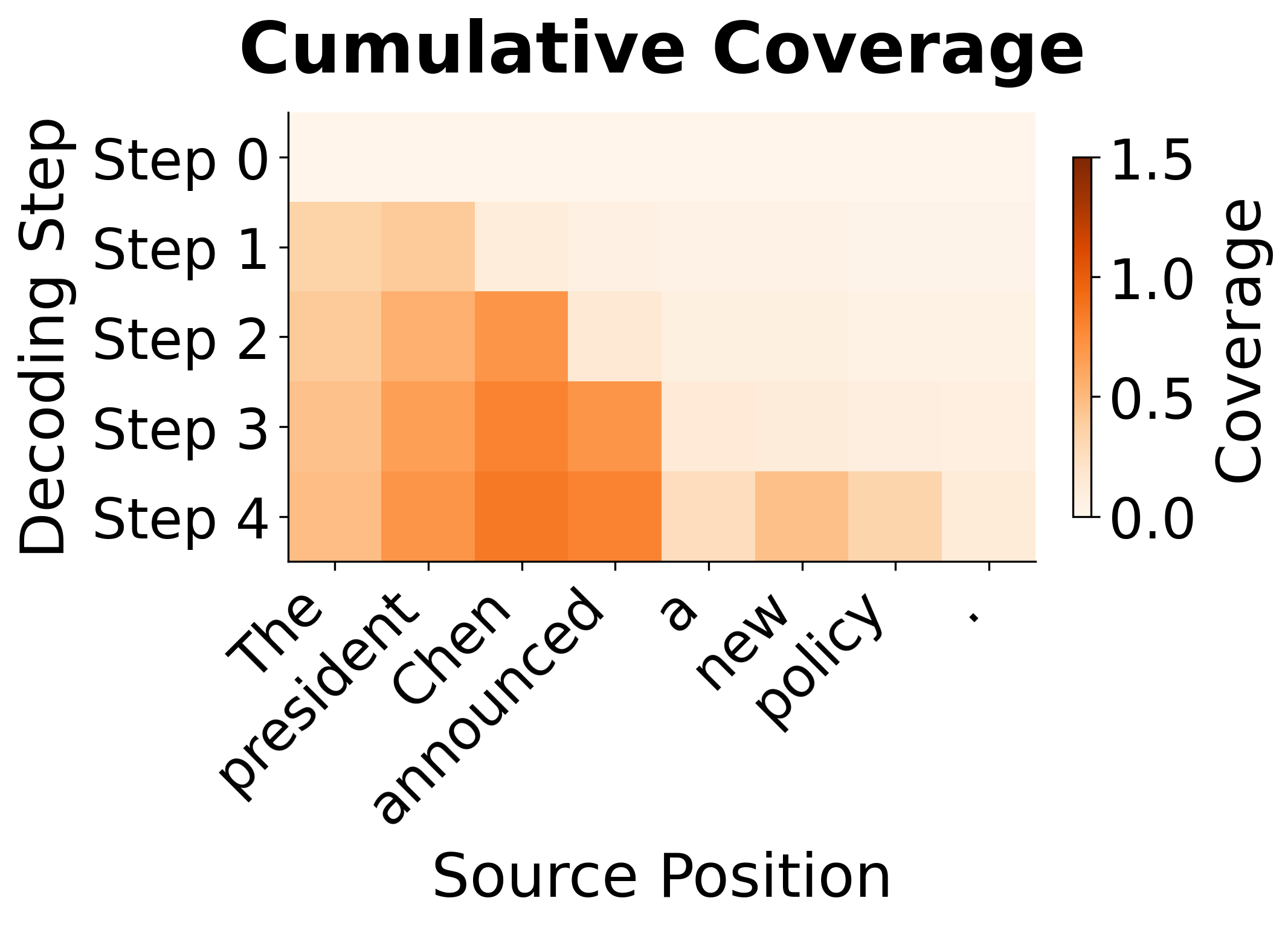
Heatmap showing cumulative coverage accumulation over decoding steps. — Cumulative coverage before each decoding step. High values (darker orange) indicate positions that have received substantial attention in previous steps, discouraging the model from re-attending to them.

The visualization shows how coverage accumulates during generation. In the left panel, each row represents the attention distribution at a single decoding step. The right panel shows the cumulative coverage before each step. Notice how "president" (position 1) quickly accumulates high coverage after step 0, discouraging the model from re-attending to it. By step 4, the coverage mechanism has effectively "used up" the early positions, encouraging the model to attend to later, less-covered positions.

Practical Training ConsiderationsLink Copied

Training pointer-generator networks requires careful attention to several practical details.

Teacher forcing with copy targets: During training, when the target token appears in the source, the model should learn to copy it. This requires computing whether each target token is copyable and adjusting the loss accordingly.

In[29]:

Code

def prepare_copy_targets(source_ids, target_ids, vocab_size):
    """
    Prepare targets for copy-aware training.

    Returns mask indicating which target tokens are copyable from source.
    """
    batch_size, tgt_len = target_ids.shape
    _, src_len = source_ids.shape

    # For each target position, check if token appears in source
    copyable = torch.zeros(batch_size, tgt_len, dtype=torch.bool)
    copy_positions = torch.zeros(batch_size, tgt_len, src_len)

    for b in range(batch_size):
        for t in range(tgt_len):
            tgt_token = target_ids[b, t].item()
            for s in range(src_len):
                if source_ids[b, s].item() == tgt_token:
                    copyable[b, t] = True
                    copy_positions[b, t, s] = 1.0

    # Normalize copy positions
    copy_positions = copy_positions / (
        copy_positions.sum(dim=-1, keepdim=True) + 1e-12
    )

    return copyable, copy_positions


# Example
source_ids = torch.tensor(
    [[5, 8, 9, 4, 10]]
)  # "the Chen Stanford said discovery"
target_ids = torch.tensor([[8, 11, 10]])  # "Chen announced discovery"

copyable, copy_pos = prepare_copy_targets(source_ids, target_ids, vocab_size=20)

def prepare_copy_targets(source_ids, target_ids, vocab_size):
    """
    Prepare targets for copy-aware training.

    Returns mask indicating which target tokens are copyable from source.
    """
    batch_size, tgt_len = target_ids.shape
    _, src_len = source_ids.shape

    # For each target position, check if token appears in source
    copyable = torch.zeros(batch_size, tgt_len, dtype=torch.bool)
    copy_positions = torch.zeros(batch_size, tgt_len, src_len)

    for b in range(batch_size):
        for t in range(tgt_len):
            tgt_token = target_ids[b, t].item()
            for s in range(src_len):
                if source_ids[b, s].item() == tgt_token:
                    copyable[b, t] = True
                    copy_positions[b, t, s] = 1.0

    # Normalize copy positions
    copy_positions = copy_positions / (
        copy_positions.sum(dim=-1, keepdim=True) + 1e-12
    )

    return copyable, copy_positions


# Example
source_ids = torch.tensor(
    [[5, 8, 9, 4, 10]]
)  # "the Chen Stanford said discovery"
target_ids = torch.tensor([[8, 11, 10]])  # "Chen announced discovery"

copyable, copy_pos = prepare_copy_targets(source_ids, target_ids, vocab_size=20)

Out[30]:

Console

Copy Target Preparation
==================================================

Source IDs: [5, 8, 9, 4, 10]
Target IDs: [8, 11, 10]

Target token analysis:
  Chen: copyable
    Copy from source position(s): [1]
  announced: must generate
  discovery: copyable
    Copy from source position(s): [4]

Additional training techniques include:

Scheduled sampling for $p_{\text{gen}}$ : Early in training, the model may not learn when to copy effectively. Some implementations use scheduled sampling to gradually shift from forced copying to learned $p_{\text{gen}}$ .
Gradient clipping: The combined distribution can have very small probabilities, leading to large gradients. Gradient clipping helps stabilize training.

Limitations and ImpactLink Copied

The copy mechanism, while powerful, has important limitations that practitioners should understand.

The mechanism assumes that words worth copying appear verbatim in the source. For tasks requiring paraphrasing or where source words need morphological changes (e.g., "announced" to "announcement"), pure copying falls short. The model must learn to generate these variants, which may still be OOV. Some extensions address this by copying at the subword level, allowing partial matches and morphological flexibility.

Copy mechanisms add computational overhead. Computing the extended vocabulary distribution and tracking OOV words increases memory usage and slows inference. For very long source documents, the attention computation over all source positions becomes expensive. Hierarchical attention and sparse attention variants can mitigate this, but at the cost of additional complexity.

The balance between copying and generating is learned implicitly through $p_{\text{gen}}$ . In practice, models sometimes over-copy, producing extractive rather than abstractive summaries, or under-copy, hallucinating facts. Careful tuning of the coverage loss weight and training data curation helps, but achieving the right balance remains challenging.

Despite these limitations, copy mechanisms significantly improved neural text generation. Before their introduction, neural summarization systems struggled with factual accuracy, producing fluent but unfaithful summaries. The pointer-generator architecture showed that neural models could preserve factual content while still generating abstractive summaries. This work paved the way for modern summarization systems and influenced the design of retrieval-augmented generation approaches that similarly blend retrieved content with generated text.

SummaryLink Copied

Copy mechanisms extend sequence-to-sequence models to handle the fundamental vocabulary limitation of neural text generation. The key concepts from this chapter:

Pointer networks use attention weights as a probability distribution over input positions, enabling the model to "point to" and copy input tokens rather than generating from a fixed vocabulary.
The generation probability $p_{\text{gen}}$ acts as a soft switch between generating from vocabulary and copying from input. It's computed from the decoder state, context vector, and input embedding, allowing the model to learn when each strategy is appropriate.
The final distribution combines generation and copy probabilities. Words appearing in both vocabulary and input receive probability from both sources, while OOV words can only be produced through copying.
Pointer-generator networks integrate these components into a practical architecture for tasks like summarization, where preserving names, numbers, and rare words is essential for factual accuracy.
OOV handling requires extending the vocabulary dynamically for each input, tracking which source positions contain which OOV words, and ensuring the loss function properly handles extended vocabulary targets.
Coverage mechanisms address repetition by tracking which source positions have been attended to and penalizing re-attention, improving output diversity and coherence.

The copy mechanism was an important step in making neural text generation practical for real-world applications where factual accuracy matters. While modern large language models have largely subsumed these techniques through massive vocabularies and in-context learning, understanding copy mechanisms provides insight into the fundamental challenges of neural text generation and the solutions researchers developed to address them.

Key ParametersLink Copied

When implementing pointer-generator networks:

Copy Switch Parameters:

hidden_dim: Dimension of encoder/decoder hidden states. Larger values capture more nuanced representations but increase computation. Typical values: 256-512 for small models, 512-1024 for larger ones.
embed_dim: Dimension of token embeddings fed to the copy switch. Should match the embedding layer used in the decoder.

Attention Parameters:

hidden_dim in attention: Must match encoder output dimension. The attention mechanism projects both encoder and decoder states to this dimension for score computation.

Coverage Parameters:

coverage_loss_weight: Hyperparameter controlling how strongly to penalize re-attending to covered positions. Values between 0.5 and 2.0 are common. Higher values reduce repetition more aggressively but may hurt fluency.

Training Parameters:

max_oov_per_batch: Maximum number of OOV words to track per batch. Limits memory usage for the extended vocabulary. Typical values: 50-200 depending on document length.
gradient_clip: Maximum gradient norm for clipping. Values around 2.0-5.0 help stabilize training when probabilities become very small.

QuizLink Copied

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about copy mechanisms in neural text generation.

Loading component...

Comments

Back to Language AI Handbook

Previous Chapter

Luong Attention

Next Chapter

Self-Attention Concept

Reference

BIBTEXAcademic

@misc{copymechanismpointernetworksforneuraltextgeneration, author = {Michael Brenndoerfer}, title = {Copy Mechanism: Pointer Networks for Neural Text Generation}, year = {2025}, url = {https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-12-16} }

APAAcademic

Michael Brenndoerfer (2025). Copy Mechanism: Pointer Networks for Neural Text Generation. Retrieved from https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation

MLAAcademic

Michael Brenndoerfer. "Copy Mechanism: Pointer Networks for Neural Text Generation." 2025. Web. 12/16/2025. <https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation>.

CHICAGOAcademic

Michael Brenndoerfer. "Copy Mechanism: Pointer Networks for Neural Text Generation." Accessed 12/16/2025. https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation.

HARVARDAcademic

Michael Brenndoerfer (2025) 'Copy Mechanism: Pointer Networks for Neural Text Generation'. Available at: https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation (Accessed: 12/16/2025).

SimpleBasic

Michael Brenndoerfer (2025). Copy Mechanism: Pointer Networks for Neural Text Generation. https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation

Direct link:

https://mbrenndoerfer.com/writing/copy-mechanism-pointer-networks-text-generation

About the author: Michael Brenndoerfer

All opinions expressed here are my own and do not reflect the views of my employer.

Michael currently works as an Associate Director of Data Science at EQT Partners in Singapore, leading AI and data initiatives across private capital investments.

With over a decade of experience spanning private equity, management consulting, and software engineering, he specializes in building and scaling analytics capabilities from the ground up. He has published research in leading AI conferences and holds expertise in machine learning, natural language processing, and value creation through data.

View Full Resume Publications Contact Books

Copy Mechanism: Pointer Networks for Neural Text Generation

Copy MechanismLink Copied

The Vocabulary Problem in GenerationLink Copied

Pointer Networks: The FoundationLink Copied

Computing the Copy ProbabilityLink Copied

Mixing Generation and CopyingLink Copied

The Pointer-Generator NetworkLink Copied

Copy Mechanism for SummarizationLink Copied

Handling Out-of-Vocabulary WordsLink Copied

Attention Visualization for CopyLink Copied

Coverage MechanismLink Copied

Practical Training ConsiderationsLink Copied

Limitations and ImpactLink Copied

SummaryLink Copied

Key ParametersLink Copied

QuizLink Copied

Comments

Reference

About the author: Michael Brenndoerfer

Related Content

Beam Search: Finding Optimal Sequences in Neural Text Generation

Teacher Forcing: Training Seq2Seq Models with Ground Truth Context

Bahdanau Attention: Dynamic Context for Neural Machine Translation

Stay updated