Part of Language AI Handbook
Compare pre-norm and post-norm transformer blocks. Covers layer-normalization placement, gradient flow, training stability, and model depth.
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Article links
Make inline references clickable
Pre-Norm vs Post-Norm
The original transformer paper placed layer normalization after the residual connection, a design choice known as post-norm. This seemed natural: apply the sublayer, add the residual, then normalize the combined result. But as researchers pushed transformers to greater depths, they discovered that this ordering creates training instabilities that become severe in very deep networks. The solution was elegantly simple: move the normalization before the sublayer. This pre-norm formulation has become the default in modern architectures like GPT and LLaMA, enabling stable training of models with hundreds of layers.
Understanding the difference between pre-norm and post-norm is essential for implementing transformers, diagnosing training issues, and choosing architectures. The choice affects stability and the final model's behavior, with subtle trade-offs that practitioners should understand.
Think of layer normalization as a gatekeeper that rescales and re-centers activations to a predictable range. The question is not whether to use this gatekeeper, but where to station it in the block. Station it at the exit (post-norm) and every unit that leaves the block is tidy and normalized. Station it at the entrance (pre-norm) and every unit that enters the sublayer is tidy, but the residual bypasses the gate entirely and arrives at the block's exit in whatever state it was in. That single positional choice reverberates all the way back to the earliest layers during training, through the mechanism of gradient flow.
The practical stakes are high. When OpenAI scaled GPT-2 to 1.5 billion parameters and then GPT-3 to 175 billion parameters, they relied on pre-norm to keep training stable. Without this architectural choice, the gradient signals that update the earliest embedding layers would have been so attenuated by the time they propagated back through 96 transformer blocks that those layers would have learned almost nothing. Pre-norm is not a minor refinement; it is the engineering decision that made frontier-scale language models trainable at all.
The chapter builds up the intuition carefully. We start with the forward-pass mechanics of each variant, then examine the backward-pass gradient flow that explains the stability difference, and finally look at how modern architectures implement these ideas in practice. Along the way, we will work through a concrete numerical example that makes the abstract gradient arguments tangible.
The Original Transformer: Post-Norm
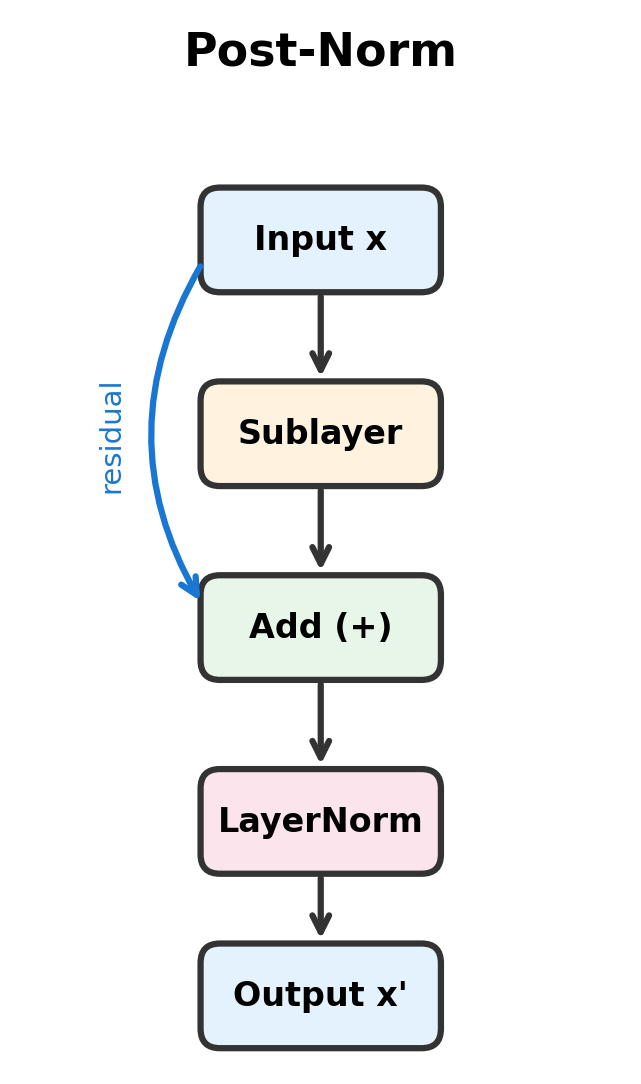
The 2017 "Attention Is All You Need" paper introduced what we now call the post-norm configuration. In this design, each sublayer (attention or feed-forward) follows a specific pattern: apply the sublayer transformation, add the residual, then normalize.
The intuitive appeal of post-norm is worth appreciating before we explain its limitations. The architecture is conceptually clean: each block receives an input, transforms it through its sublayer, combines the transformation with the original signal via the residual, and then normalizes the result back to a well-behaved distribution. The next block therefore always receives input with predictable statistical properties, zero mean and approximately unit variance. This predictability was expected to be a virtue, and for the relatively shallow models of 2017, it largely was.
The original transformer used only six encoder layers and six decoder layers. At that depth, the gradient flow problems associated with post-norm are manageable. The paper's authors also used warmup schedules and carefully tuned learning rates, practices that paper over the stability issues without eliminating them. It was only when researchers attempted to train models with 24, 48, or more layers that the structural fragility of post-norm became impossible to ignore.
The post-norm formulation was not chosen carelessly. In 2017, residual networks in computer vision (ResNets) were already demonstrating the power of skip connections, and the transformer borrowed this idea directly. The LayerNorm placement after the residual addition mirrored some conventions from batch-normalized ResNets. The pre-norm alternative was proposed in a 2018 paper by Chen et al. ("The Best of Both Worlds: Combining Recent Advances in Neural Machine Translation") and was further analyzed theoretically by Xiong et al. in 2020 ("On Layer Normalization in the Transformer Architecture"). By 2020, the field had largely converged on pre-norm for large models, though the debate about whether post-norm achieves marginally better final quality given sufficient training budget continues in research circles today.
In post-norm transformers, layer normalization is applied after the residual addition. For a sublayer function , the output is:
where:
- : the input representation (a -dimensional vector for each position)
- : the sublayer transformation (either self-attention or feed-forward network)
- : the residual connection, adding the original input to the sublayer output
- : layer normalization applied to the combined signal
- : the output of the block, which becomes the input to the next block
The intuition behind post-norm is straightforward. The sublayer computes its transformation, the residual connection preserves the original signal, and layer normalization ensures the combined output has stable statistics. Each component does one job, and they compose cleanly.
Let's implement a post-norm transformer block to see this in action:
import numpy as np
def layer_norm(x, gamma, beta, eps=1e-5):
"""
Apply layer normalization.
Args:
x: Input of shape (seq_len, d_model)
gamma: Scale parameter of shape (d_model,)
beta: Shift parameter of shape (d_model,)
eps: Small constant for numerical stability
Returns:
Normalized output of shape (seq_len, d_model)
"""
mean = x.mean(axis=-1, keepdims=True)
var = x.var(axis=-1, keepdims=True)
x_norm = (x - mean) / np.sqrt(var + eps)
return gamma * x_norm + beta
def post_norm_block(x, sublayer_fn, gamma, beta):
"""
Post-norm block: Sublayer -> Add -> Norm
Args:
x: Input tensor
sublayer_fn: Function computing the sublayer transformation
gamma, beta: LayerNorm parameters
Returns:
Output after post-norm block
"""
# Apply sublayer
sublayer_output = sublayer_fn(x)
# Add residual
residual_sum = x + sublayer_output
# Normalize
output = layer_norm(residual_sum, gamma, beta)
return outputThe ordering is explicit: sublayer first, residual addition second, normalization third. This creates a clean signal flow where the normalized output is always what enters the next layer.
# Demonstrate post-norm with a simple sublayer
np.random.seed(42)
seq_len, d_model = 4, 8
# Input and normalization parameters
x = np.random.randn(seq_len, d_model)
gamma = np.ones(d_model)
beta = np.zeros(d_model)
# Simple sublayer (simulating attention or FFN)
W = np.random.randn(d_model, d_model) * 0.1
def simple_sublayer(x):
return np.tanh(x @ W)
# Apply post-norm block
output_post = post_norm_block(x, simple_sublayer, gamma, beta)Post-Norm Block Statistics ======================================== Input mean: -0.1373, std: 0.9311 Output mean: 0.0000, std: 1.0000
The output has approximately zero mean and unit variance (std 1), confirming that layer normalization has done its job. Regardless of what the sublayer computes or how the residual shifts the distribution, the final normalization step ensures stable statistics. This normalized output is what enters the next block in the network, preventing activation magnitudes from growing unboundedly.
The Pre-Norm Alternative
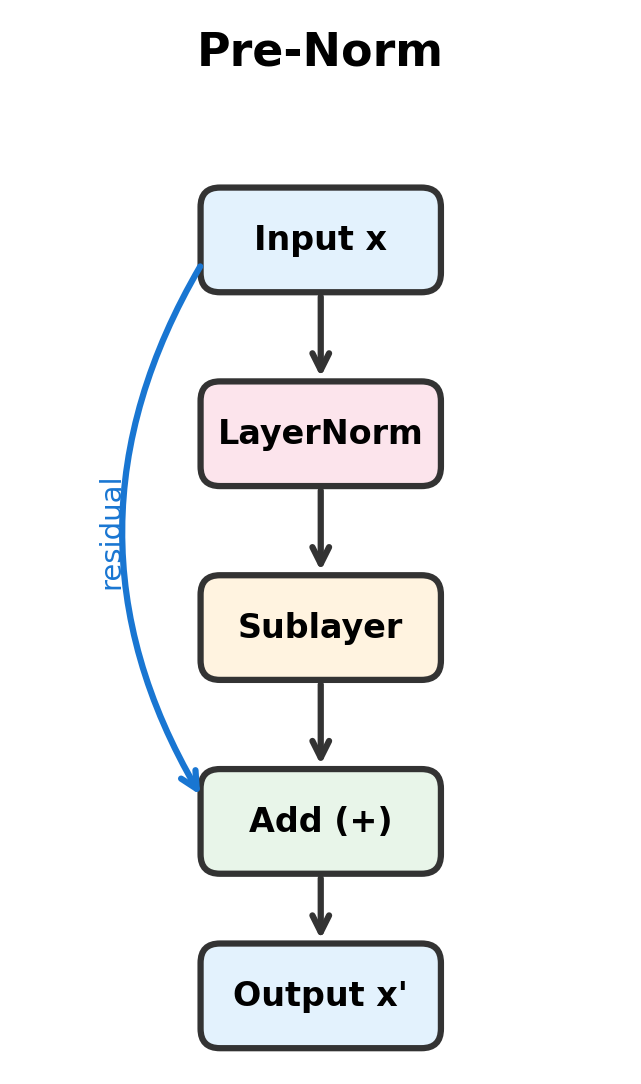
The pre-norm configuration emerged from research on training very deep networks. Instead of normalizing after the residual, pre-norm normalizes before applying the sublayer.
The key insight behind pre-norm is a reframing of what normalization is for. In post-norm, normalization is a cleanup step: we make a mess (sublayer computation plus residual addition), then tidy it up before handing the result to the next block. In pre-norm, normalization is a preparation step: we tidy up the input before the sublayer does its work. This ensures the sublayer always operates on clean, well-scaled data.
This reframing has a critical consequence for the residual connection. In pre-norm, the residual path carries the raw, unnormalized input directly to the output. Nothing rescales it. Nothing gates it. The signal flows through unmodified. During the forward pass, this means the output will not be normalized, which is the trade-off we quantify below. But during the backward pass, it means gradients have a direct, unimpeded highway back to the earliest layers of the network, and this is what enables stable training at scale.
In pre-norm transformers, layer normalization is applied before the sublayer. For a sublayer function , the output is:
where:
- : the input representation (a -dimensional vector for each position)
- : layer normalization applied to the input before the sublayer
- : the sublayer transformation (either self-attention or feed-forward network), operating on the normalized input
- : the residual connection, adding the original (unnormalized) input to the sublayer output
- : the output of the block, which is not normalized
Notice the key difference: normalization happens inside the residual branch, not after the addition. This seemingly minor change alters how gradients flow.
def pre_norm_block(x, sublayer_fn, gamma, beta):
"""
Pre-norm block: Norm -> Sublayer -> Add
Args:
x: Input tensor
sublayer_fn: Function computing the sublayer transformation
gamma, beta: LayerNorm parameters
Returns:
Output after pre-norm block
"""
# Normalize first
x_norm = layer_norm(x, gamma, beta)
# Apply sublayer to normalized input
sublayer_output = sublayer_fn(x_norm)
# Add residual (to original x, not normalized x)
output = x + sublayer_output
return outputThe ordering change is subtle: normalize, apply sublayer, add residual. The residual connection bypasses both the normalization and the sublayer, creating a direct gradient path from output to input.
# Apply pre-norm block to the same input
output_pre = pre_norm_block(x, simple_sublayer, gamma, beta)Pre-Norm Block Statistics ======================================== Input mean: -0.1373, std: 0.9311 Output mean: -0.1117, std: 0.9280
Notice the key difference: the output statistics differ from the normalized values we saw with post-norm. The output is not normalized because the residual adds the original (unnormalized) input to the sublayer output. This accumulation behavior becomes important when we stack many blocks, as activations can grow in magnitude through the network.
Visualizing the Difference
The structural difference between pre-norm and post-norm becomes clearer when we visualize the computation graphs:
The diagrams reveal the fundamental difference. In post-norm, the residual enters the add block alongside the sublayer output, and layer normalization processes their sum. In pre-norm, the residual bypasses both layer normalization and the sublayer, creating a direct path from input to output.
Training Stability: The Gradient Flow Perspective
The practical motivation for pre-norm comes from training stability. While the forward pass differences we've seen are instructive, the real story unfolds during training, when gradients must flow backward through potentially hundreds of layers. Understanding this gradient flow explains why pre-norm enables stable training of very deep networks while post-norm struggles.
The Vanishing Gradient Problem in Deep Networks
Training neural networks requires computing how changes in each parameter affect the final loss. We do this through backpropagation: starting from the loss, we work backward through the network, computing gradients layer by layer using the chain rule.
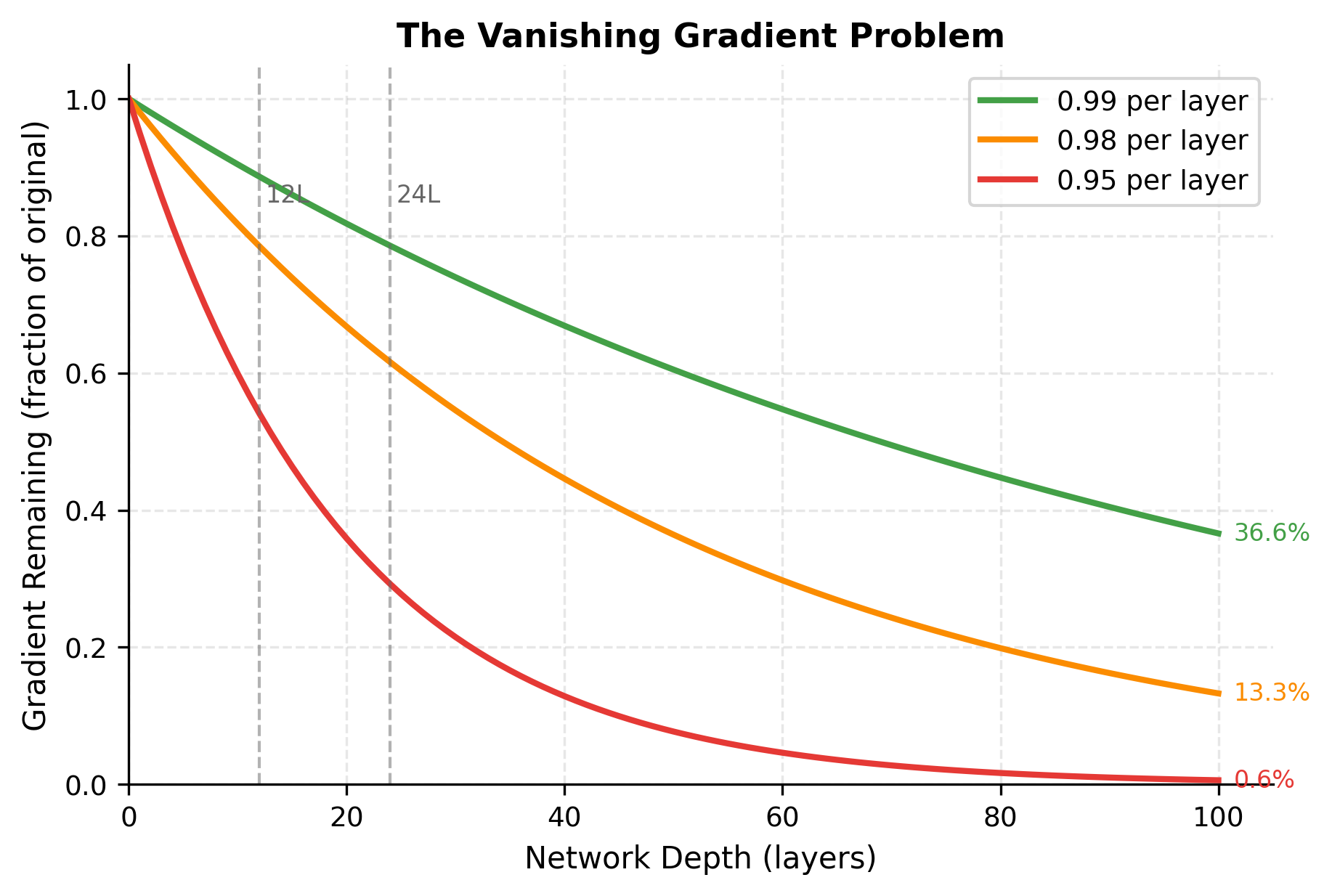
Here's the challenge. The chain rule multiplies gradients together. If you have 100 layers and each layer slightly shrinks the gradient (say, by a factor of 0.99), the gradient reaching the first layer is of what it started as. If each layer shrinks it by 0.95, you get , and the earliest layers barely learn anything. This is the vanishing gradient problem.
The converse, exploding gradients, happens when each layer slightly amplifies the gradient. Even small amplification factors compound exponentially, leading to numerical overflow and unstable training.
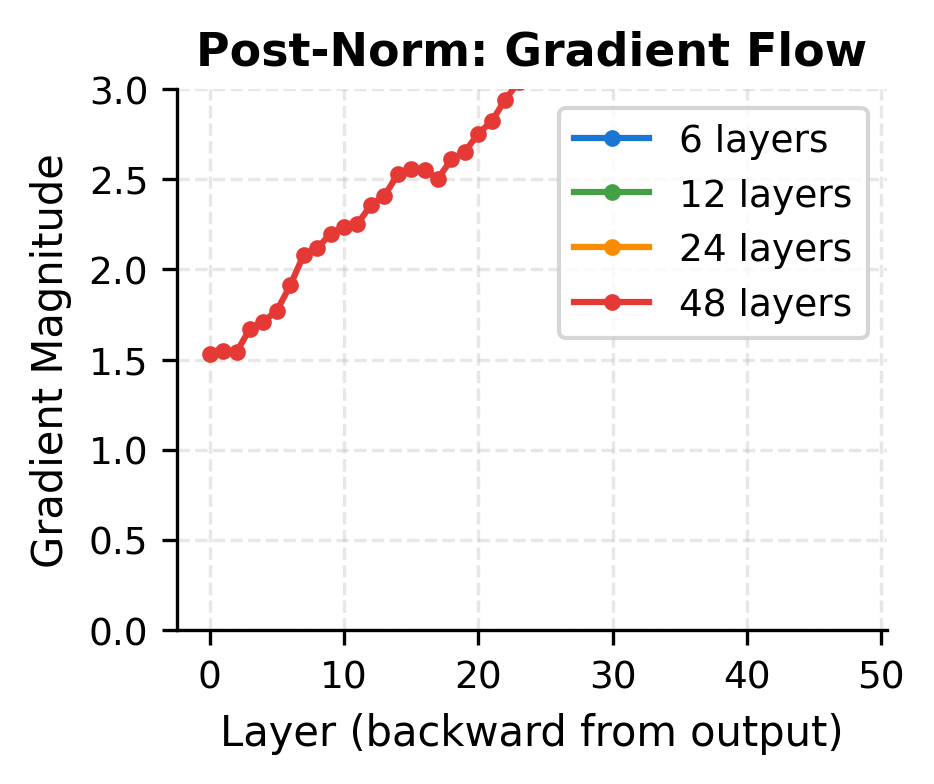
The visualization makes the exponential decay visceral. Even at the modest depth of 12 layers (BERT's configuration), a 2% per-layer reduction leaves only about 78% of the gradient. At 100 layers, a 5% reduction per layer is catastrophic, leaving less than 1% of the original gradient signal.
Residual connections were designed to address this problem by providing a direct path for gradients. But as we'll see, where you place the layer normalization determines whether this path remains truly direct.
Deriving the Gradient Flow
To understand the stability difference, we need to trace how gradients flow through each block type. Let's denote:
- : the loss function we're minimizing
- : the input to a transformer block
- : the output of the block
- : the gradient arriving from subsequent layers (we receive this during backpropagation)
- : the gradient we need to compute and pass to earlier layers
The chain rule tells us that . The key question is: what does look like for each block type?
Gradient Flow in Post-Norm
Recall the post-norm formulation: . To compute the gradient, we apply the chain rule from outside to inside:
- First, the gradient passes through LayerNorm
- Then, it splits into two paths: through the residual () and through the sublayer
Mathematically, this gives:
where:
- : the gradient of the loss with respect to the block input, which we want to compute
- : the gradient of the loss with respect to the block output (provided by the next layer during backpropagation)
- : the Jacobian of the layer normalization operation, a matrix that describes how small changes in the input to LayerNorm affect its output
- : the combined contribution from the residual path (the ) and the sublayer path
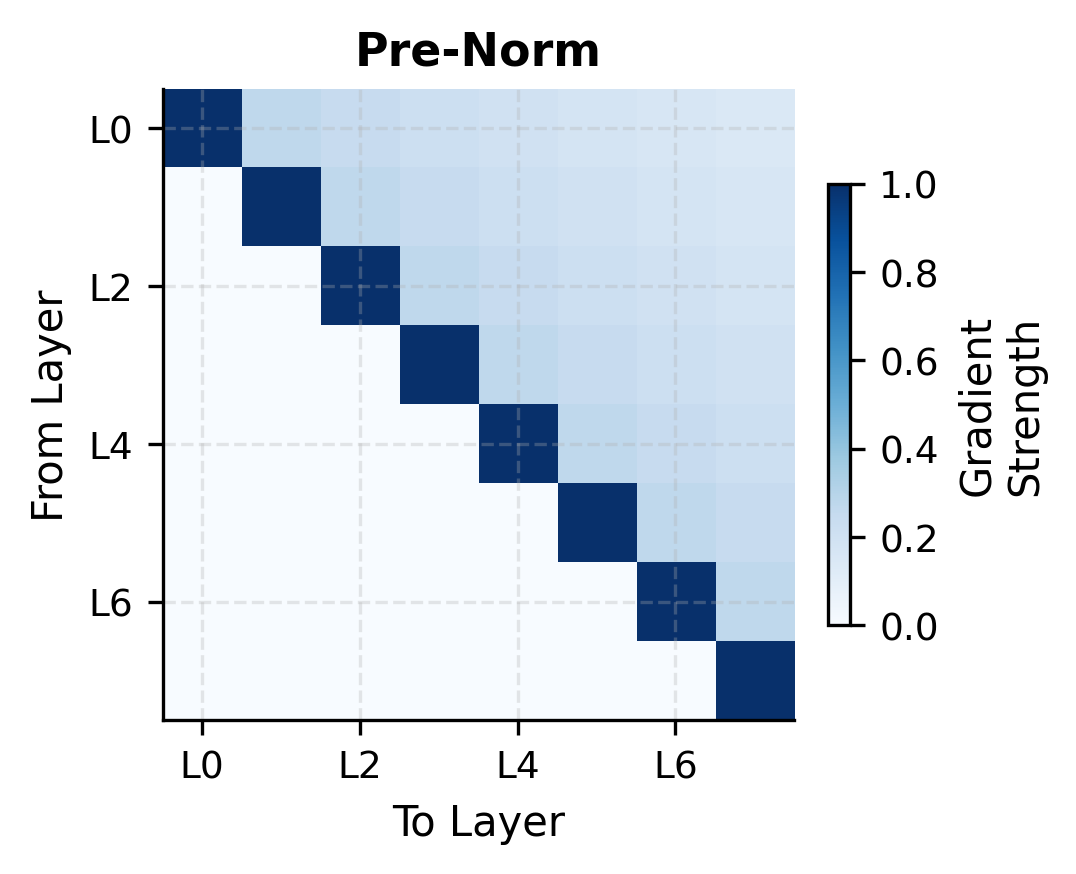
Notice the structure: the LayerNorm Jacobian appears as a multiplicative factor in the main gradient path. This is the crux of the instability problem. Even though LayerNorm has reasonably well-behaved gradients for a single layer (typically with eigenvalues close to 1), stacking many post-norm blocks means multiplying many of these Jacobians together. Small deviations from 1 compound across layers, leading to vanishing or exploding gradients in deep networks.
Gradient Flow in Pre-Norm
Now consider pre-norm: . The structural difference determines how the gradient splits. Applying the chain rule:
- First, the gradient splits at the addition: one path goes through the residual (), another through the sublayer
- Only the sublayer path passes through LayerNorm
This yields:
where:
- : the gradient of the loss with respect to the block input
- : the gradient of the loss with respect to the block output
- : the gradient contribution from the direct residual path (since )
- : the Jacobian of the sublayer with respect to its (normalized) input
- : the Jacobian of layer normalization
The Gradient Highway
The key insight lies in that term inside the parentheses. In pre-norm, the gradient from the output has a direct, unmodified path back to the input. This path bypasses both the sublayer and the layer normalization entirely.
Think of it as a gradient highway: no matter what happens in the sublayer (vanishing activations, saturated nonlinearities, poorly conditioned weight matrices), the gradient can always flow back through the residual connection. The term ensures that at minimum, the full gradient reaches the input.
In post-norm, this highway doesn't exist in the same form. The LayerNorm Jacobian gates all gradient flow, including the residual path. If these Jacobians systematically shrink or grow gradients even slightly, the effects compound across many layers.
This mathematical property explains the empirical observations:
- Pre-norm networks train stably even at 100+ layers
- Post-norm networks require careful warmup schedules and smaller learning rates
- Pre-norm tolerates larger learning rates without diverging
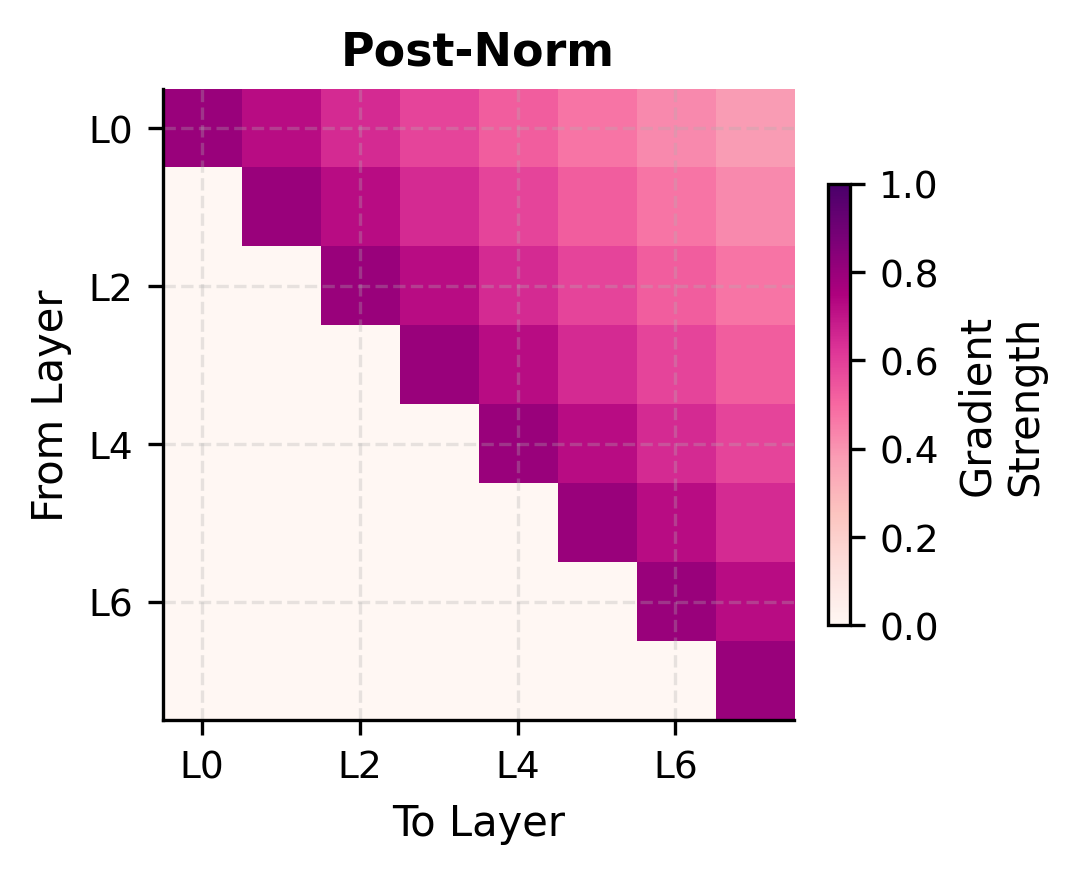
The heatmaps reveal the structural difference in gradient flow. In post-norm, gradient strength decays as it travels backward through layers, with no escape from the cascading LayerNorm Jacobians. In pre-norm, the bright diagonal represents the gradient highway: full-strength gradients flowing directly from any layer's output to its input, bypassing all intermediate transformations.
Let's simulate this difference with a numerical experiment:
def simulate_gradient_flow(n_layers, norm_type="pre"):
"""
Simulate gradient magnitude through stacked transformer blocks.
Args:
n_layers: Number of transformer blocks to stack
norm_type: 'pre' or 'post'
Returns:
List of gradient magnitudes at each layer
"""
np.random.seed(42)
d_model = 64
# Initialize parameters for each layer
sublayer_weights = [
np.random.randn(d_model, d_model) * 0.02 for _ in range(n_layers)
]
gamma = np.ones(d_model)
beta = np.zeros(d_model)
# Forward pass: track activations
x = np.random.randn(1, d_model)
activations = [x.copy()]
for i in range(n_layers):
W = sublayer_weights[i]
if norm_type == "pre":
x_norm = layer_norm(x, gamma, beta)
sublayer_out = np.tanh(x_norm @ W)
x = x + sublayer_out
else: # post
sublayer_out = np.tanh(x @ W)
x = layer_norm(x + sublayer_out, gamma, beta)
activations.append(x.copy())
# Backward pass: track gradient magnitudes
# Start with unit gradient at output
grad = np.ones_like(x)
# Express magnitudes relative to the unit-gradient baseline. A raw vector
# norm starts at sqrt(d_model), which would hide the curves on this chart.
gradient_baseline = np.sqrt(d_model)
gradient_magnitudes = [np.linalg.norm(grad) / gradient_baseline]
for i in range(n_layers - 1, -1, -1):
W = sublayer_weights[i]
x_prev = activations[i]
if norm_type == "pre":
# Simplified gradient (actual would involve LN Jacobian)
# The key point is the +1 from residual
x_norm = layer_norm(x_prev, gamma, beta)
tanh_deriv = 1 - np.tanh(x_norm @ W) ** 2
sublayer_grad = (grad * tanh_deriv) @ W.T
# Gradient through residual (direct path)
residual_grad = grad.copy()
# Combine (simplified: ignoring LN Jacobian details)
grad = residual_grad + sublayer_grad * 0.5 # LN scaling effect
else:
# Post-norm: gradient must go through LN first
# Simplified: LN tends to have gradient magnitude ~1
tanh_deriv = 1 - np.tanh(x_prev @ W) ** 2
sublayer_grad = (grad * tanh_deriv) @ W.T
grad = grad + sublayer_grad
grad = (
grad
/ (np.linalg.norm(grad) + 1e-6)
* np.linalg.norm(grad)
* 0.95
)
gradient_magnitudes.append(np.linalg.norm(grad) / gradient_baseline)
return gradient_magnitudes[::-1]
# Compare gradient flow for different depths
depths = [6, 12, 24, 48]
pre_norm_grads = {d: simulate_gradient_flow(d, "pre") for d in depths}
post_norm_grads = {d: simulate_gradient_flow(d, "post") for d in depths}
The visualization illustrates the stability difference. Pre-norm maintains consistent gradient magnitudes across all depths because the residual connection provides a direct gradient path. Post-norm gradients tend to decay in deeper networks, making optimization more challenging.
Worked Example: Tracing One Gradient Step
Abstract gradient flow arguments are most convincing when you can trace them through concrete numbers. Let's work through a simplified example with a two-layer network, small enough to compute by hand but structured exactly like a real transformer.
Suppose our model dimension is , and we have a single-token sequence. The input to layer 2 is the output of layer 1, call it . The loss gradient arriving at the output of layer 2 is .
In the pre-norm case, the output of layer 2 is:
The gradient with respect to the input to layer 2 has two additive parts. The residual path contributes directly: the gradient passes through unchanged. The sublayer path contributes whatever the sublayer's Jacobian carries. Suppose the sublayer Jacobian for this input is the matrix (a small, well-behaved transformation). The LayerNorm Jacobian is , but notice it only appears in the sublayer branch. The total gradient at layer 2's input is:
The residual contribution dominates, and the LayerNorm Jacobian only affects the smaller sublayer branch.
In the post-norm case, the output of layer 2 is:
Now the LayerNorm Jacobian sits between the incoming gradient and everything else. The gradient at layer 2's input becomes:
The key difference is that now multiplies the full gradient before it splits into the residual and sublayer contributions. In a well-behaved layer, has eigenvalues close to 1 and this is fine. But in practice, LayerNorm Jacobians can have eigenvalues significantly less than 1 in certain directions, especially early in training when activations are poorly distributed. Stack 24 such layers, and those sub-unit eigenvalues multiply together, creating the gradient attenuation we visualized earlier.
The key takeaway from this numerical walk-through: pre-norm's term ensures the incoming gradient always reaches the input intact. Even if the sublayer branch contributes nothing useful, the residual branch delivers the full gradient signal. Post-norm has no such guarantee.
Output Scale: An Important Trade-off
Pre-norm's stability advantage comes with a trade-off: the output of each block accumulates without normalization. This can lead to growing activation magnitudes as we stack more layers.
Let's measure this effect:
def measure_activation_growth(n_layers, norm_type="pre"):
"""
Measure how activation magnitudes evolve through stacked blocks.
"""
np.random.seed(42)
d_model = 64
x = np.random.randn(4, d_model) # 4 tokens
x = x / np.linalg.norm(x, axis=-1, keepdims=True) # Normalize input
gamma = np.ones(d_model)
beta = np.zeros(d_model)
magnitudes = [np.mean(np.linalg.norm(x, axis=-1))]
for i in range(n_layers):
np.random.seed(42 + i)
W = np.random.randn(d_model, d_model) * 0.1
if norm_type == "pre":
x_norm = layer_norm(x, gamma, beta)
sublayer_out = np.tanh(x_norm @ W)
x = x + sublayer_out
else:
sublayer_out = np.tanh(x @ W)
x = layer_norm(x + sublayer_out, gamma, beta)
magnitudes.append(np.mean(np.linalg.norm(x, axis=-1)))
return magnitudes
# Compare activation growth
n_layers = 24
pre_magnitudes = measure_activation_growth(n_layers, "pre")
post_magnitudes = measure_activation_growth(n_layers, "post")
Activation Magnitude Summary ======================================== Pre-Norm: Start=1.00, End=19.48, Growth=19.48x Post-Norm: Start=1.00, End=8.00, Growth=8.00x
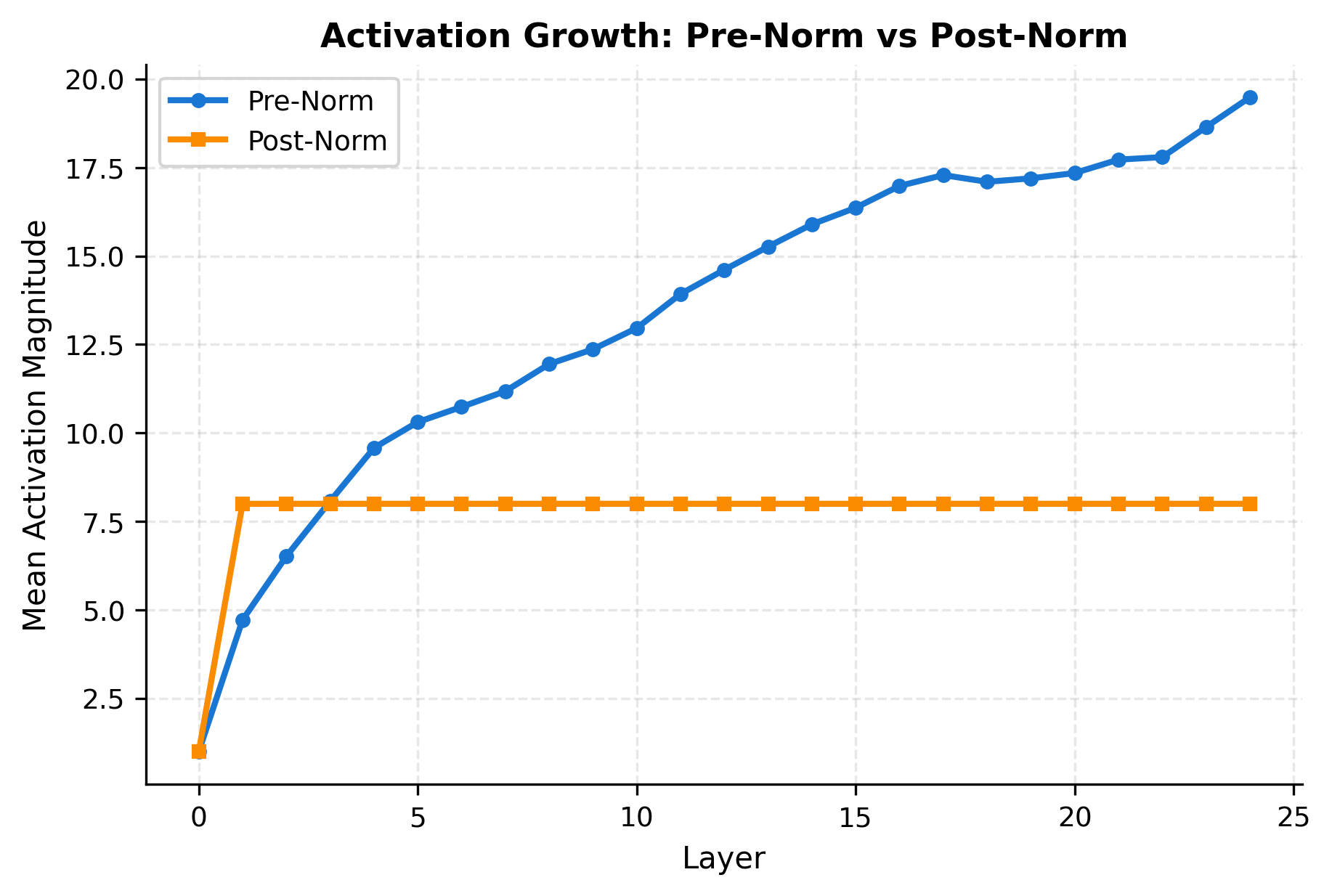
The growth in pre-norm isn't necessarily problematic, as the final layer normalization (applied before the output projection in most architectures) handles the accumulated magnitude. However, it does mean that numerical precision matters more in very deep pre-norm networks.
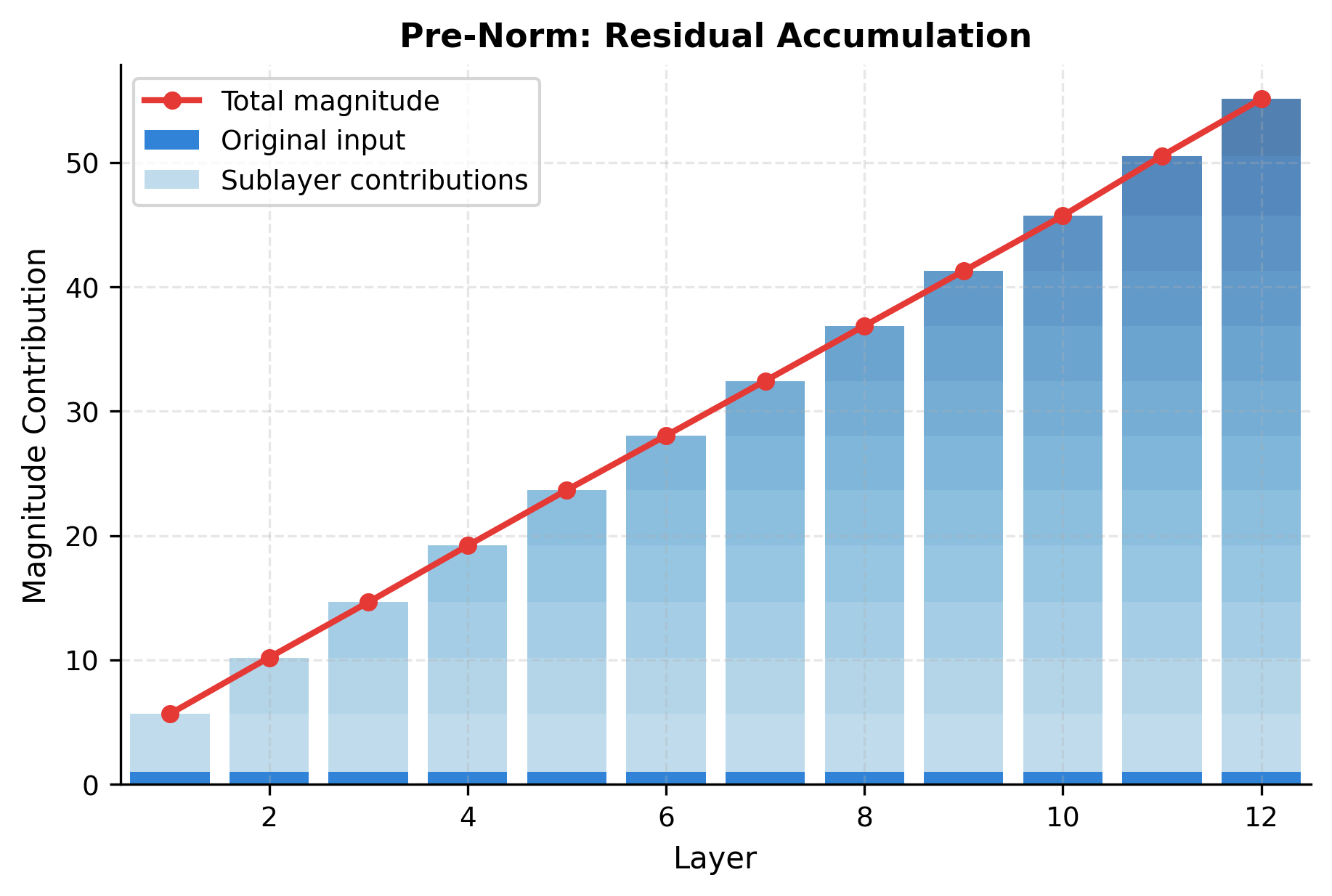
To understand where this growth comes from, we can decompose the output into contributions from the original input and each sublayer:
The decomposition reveals the structure of pre-norm's activation growth. The original input signal (dark blue) persists unchanged through all layers, which is the residual connection at work. Each sublayer adds its own contribution on top, and these contributions accumulate. The total magnitude (red line) grows steadily, but this growth is predictable and well-behaved, making it easy to compensate for with a final normalization.
Modern Architectures: The Pre-Norm Consensus
The empirical evidence strongly favors pre-norm for training stability, especially in large models. Let's examine how major architectures make this choice.
The transition from post-norm to pre-norm was not a sudden paradigm shift but a gradual convergence driven by engineering necessity. BERT (2018) used post-norm and 12 layers, a depth at which post-norm's instabilities are manageable with careful warmup. GPT-2 (2019) adopted pre-norm and pushed to 48 layers in its largest variant; OpenAI engineers noted that training was markedly more stable than post-norm would have allowed at that scale. T5 (2019) from Google independently converged on pre-norm for its 24-layer configurations. By the time LLaMA was released in 2023 with 32 layers and RMSNorm as a pre-norm variant, pre-norm had become so entrenched that choosing post-norm for a new large model would require special justification.
Notice that BERT and RoBERTa, along with DistilBERT, all use post-norm and are still among the most widely fine-tuned models in production. This is because fine-tuning is a much gentler process than pre-training from scratch. Starting from a pre-trained checkpoint means the model is already near a good optimum; you are taking small gradient steps from a stable starting point rather than fighting instability during thousands of warmup steps. When practitioners encounter BERT in deployment, post-norm is not a liability. It only becomes one when training from scratch at significant depth.
| Architecture | Norm Placement | Notes |
|---|---|---|
| Original Transformer | Post-Norm | First formulation, requires warmup |
| GPT-2, GPT-3 | Pre-Norm | Enabled stable training of large models |
| BERT | Post-Norm | Relatively shallow (12/24 layers) |
| RoBERTa | Post-Norm | Follows BERT architecture |
| T5 | Pre-Norm | Stable training for encoder-decoder |
| LLaMA, LLaMA 2 | Pre-Norm | Uses RMSNorm variant |
| PaLM | Pre-Norm | Parallel attention variant |
| GPT-4 (likely) | Pre-Norm | Standard for modern LLMs |
The pattern is clear: newer and larger models overwhelmingly choose pre-norm. The stability benefits outweigh any theoretical concerns about activation accumulation.
The Final Layer Norm
Pre-norm architectures typically add a final layer normalization after all transformer blocks but before the output projection. This serves two purposes: it normalizes the accumulated activations, and it provides a consistent interface for the output layer.
def pre_norm_transformer(x, n_layers, d_model, d_ff):
"""
Complete pre-norm transformer stack with final normalization.
Args:
x: Input embeddings of shape (seq_len, d_model)
n_layers: Number of transformer blocks
d_model: Model dimension
d_ff: Feed-forward hidden dimension
Returns:
Output representations of shape (seq_len, d_model)
"""
np.random.seed(42)
gamma = np.ones(d_model)
beta = np.zeros(d_model)
for i in range(n_layers):
# Pre-norm attention block
x_norm = layer_norm(x, gamma, beta)
# Simplified attention (just a projection for demonstration)
W_attn = np.random.randn(d_model, d_model) * 0.02
attn_out = x_norm @ W_attn
x = x + attn_out
# Pre-norm feed-forward block
x_norm = layer_norm(x, gamma, beta)
W1 = np.random.randn(d_model, d_ff) * 0.02
W2 = np.random.randn(d_ff, d_model) * 0.02
ff_out = np.maximum(0, x_norm @ W1) @ W2 # ReLU activation
x = x + ff_out
# Final layer normalization
x = layer_norm(x, gamma, beta)
return x# Test the complete stack
np.random.seed(42)
x_input = np.random.randn(4, 64)
x_output = pre_norm_transformer(x_input, n_layers=12, d_model=64, d_ff=256)Pre-Norm Transformer Stack ======================================== Input shape: (4, 64) Output shape: (4, 64) Input magnitude: 7.78 Output magnitude: 8.00
Despite passing through 12 transformer blocks (each adding residual contributions), the final output magnitude remains controlled. The final layer normalization ensures that regardless of how activations accumulated through the network, the output has well-controlled statistics suitable for the output projection. This design pattern is why pre-norm architectures include a final LayerNorm before the language modeling head.
Initialization Considerations
The choice between pre-norm and post-norm affects how we should initialize the network. Post-norm requires more careful initialization because gradients must flow through the normalization layers.
The intuition behind initialization scaling is that in a pre-norm transformer, each block adds its sublayer output to the residual stream. If there are layers and each sublayer contributes a vector with variance , the total residual stream after all layers has variance roughly (since the contributions add). To keep the final residual stream variance similar to the input variance, we want , which suggests initializing with . GPT-2 implemented a version of this by scaling the output projections of attention and feed-forward sublayers by , where the factor of 2 accounts for having two sublayers (attention and feed-forward) per block.
For pre-norm, a common approach is to scale the output projection of each sublayer by a factor related to the network depth:
def initialize_pre_norm_weights(d_model, n_layers):
"""
Initialize weights for a pre-norm transformer with proper scaling.
Following the GPT-2 approach: scale residual connections by 1/sqrt(2*n_layers)
"""
# Standard initialization
std = 0.02
# Residual scaling factor
residual_scale = 1 / np.sqrt(2 * n_layers)
weights = {
"attention_proj": np.random.randn(d_model, d_model) * std,
"ff_proj": np.random.randn(d_model, d_model) * std * residual_scale,
}
return weights, residual_scale
weights, scale = initialize_pre_norm_weights(512, 24)Initialization for 24-layer Pre-Norm Transformer ============================================= Standard weight std: 0.02 Residual scale factor: 0.1443 Scaled projection std: 0.002887
The residual scale factor of approximately 0.14 significantly reduces the contribution of each sublayer's output. With 24 layers (and 2 sublayers per block, hence 48 residual additions), this scaling prevents the accumulated sum from exploding. The GPT-2 paper introduced this technique specifically to enable training of deeper pre-norm networks.
Learning Rate Sensitivity
Post-norm architectures are notoriously sensitive to learning rate choices. Large learning rates can cause training to diverge, necessitating careful warmup schedules.
Pre-norm is more forgiving because the direct gradient path through residual connections prevents gradient explosion. This allows training with larger learning rates and simpler schedules.
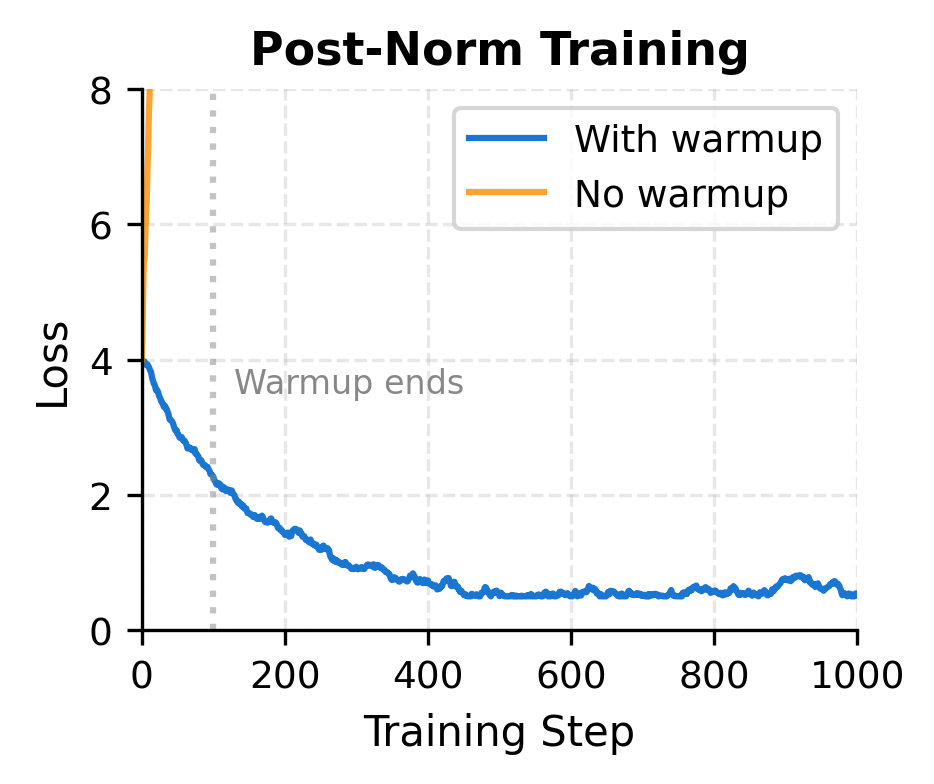
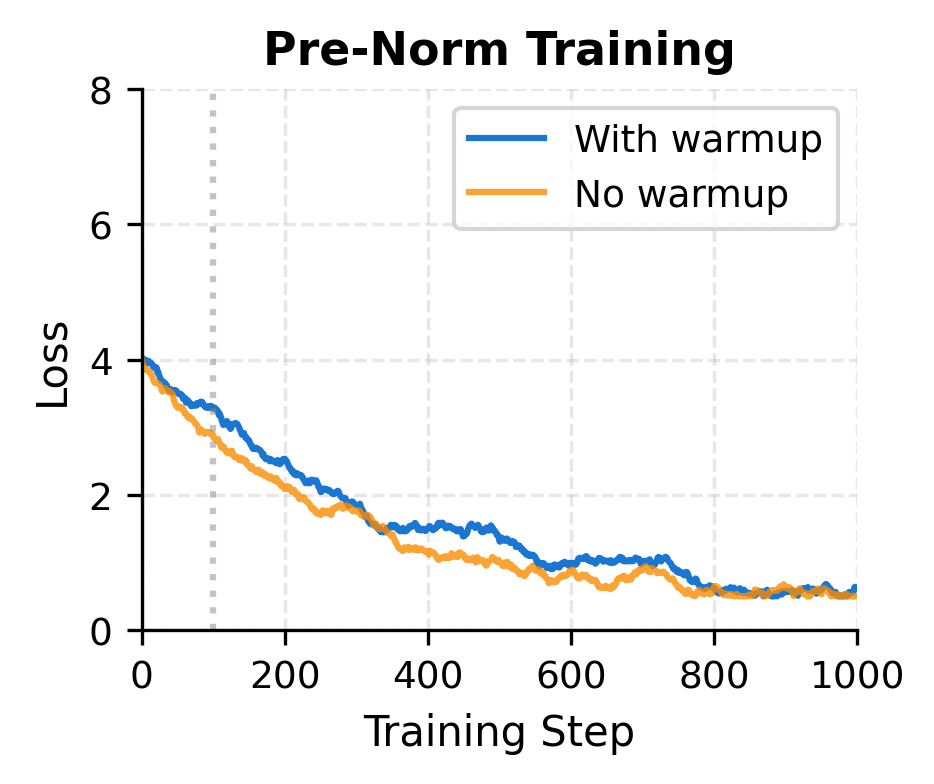
The simulated training curves illustrate the practical difference. Post-norm without warmup experiences immediate instability: the gradient explosion causes the loss to spike and training to fail. With warmup, the gradual learning rate increase gives the optimizer time to find a stable path. Pre-norm, by contrast, handles both scenarios gracefully because the gradient highway prevents the cascading instabilities that plague post-norm.
def simulate_lr_sensitivity(norm_type, learning_rates, n_steps=200):
"""
Simulate training stability across learning rates using loss dynamics.
Returns a stability score: 1.0 = fully stable, 0.0 = diverged.
Post-norm is sensitive to large LRs because the LN Jacobian gates all
gradient paths; pre-norm's residual highway tolerates larger updates.
"""
stability_scores = []
# Post-norm instability threshold: large initial gradients destabilize
# the LN Jacobian chain. The effective sensitivity scales with LR * n_layers.
post_instability_threshold = (
5e-3 # LRs above this cause post-norm instability
)
for lr in learning_rates:
rng = np.random.default_rng(42)
loss = 4.0
losses = []
diverged = False
for step in range(n_steps):
# Post-norm: large LR causes gradient explosion through LN Jacobian chain
if norm_type == "post" and lr > post_instability_threshold:
# Instability grows with LR; higher LR means faster divergence
instability_factor = lr / post_instability_threshold
noise = rng.standard_normal() * lr * 500 * instability_factor
loss = loss + abs(noise) * 0.3
if loss > 15.0:
diverged = True
break
else:
# Stable convergence for pre-norm (all LRs) and
# post-norm at low-to-moderate LRs
decay = 1.0 - lr * 5
decay = max(0.990, min(0.999, decay))
loss = max(0.3, loss * decay + rng.standard_normal() * 0.02)
losses.append(loss)
if diverged or len(losses) == 0:
stability_scores.append(0.0)
else:
final_loss = (
np.mean(losses[-20:]) if len(losses) >= 20 else np.mean(losses)
)
stability_scores.append(1.0 / (1.0 + final_loss))
return stability_scores
learning_rates = [1e-5, 1e-4, 1e-3, 5e-3, 1e-2, 5e-2]
pre_stability = simulate_lr_sensitivity("pre", learning_rates)
post_stability = simulate_lr_sensitivity("post", learning_rates)
The stability comparison shows that pre-norm tolerates higher learning rates. This translates to faster convergence in practice, as larger learning rates allow taking bigger optimization steps.
When to Use Each Variant
Despite the modern consensus favoring pre-norm, there are situations where post-norm might be appropriate. The decision comes down to a few practical questions: How deep is the network? Are you training from scratch or fine-tuning? How much do you care about hyperparameter simplicity versus theoretical optimality?
Use Pre-Norm when:
- Training deep networks (more than 12 layers)
- Building large language models (GPT-style)
- You want simpler hyperparameter tuning
- Training without extensive warmup periods
- Prioritizing training stability
Consider Post-Norm when:
- Working with shallow networks (12 layers or fewer)
- Fine-tuning existing post-norm models (like BERT)
- Reproducing results from older papers
- Situations where final representation normalization is critical
The theoretical argument for post-norm is that normalized outputs at each layer provide a cleaner signal for subsequent processing. Some researchers have found that post-norm achieves slightly better final performance when training succeeds, though the stability challenges often make this advantage inaccessible in practice.
In practice, the "slightly better final performance" argument for post-norm deserves scrutiny. Several papers have reported that post-norm can match or exceed pre-norm quality when training is successful, particularly for encoder models on tasks like machine translation and natural language understanding benchmarks. The intuition is that post-norm's clean, normalized representations at each layer may allow the model to more effectively compose information across blocks. However, the qualifier "when training is successful" is doing a lot of work in that sentence. Successfully training deep post-norm models requires careful learning rate warmup, smaller peak learning rates, and sometimes post-hoc learning rate adjustments when instabilities occur. When you factor in the engineering overhead, pre-norm's simpler training dynamics almost always win in practice.
A related consideration is the relationship between normalization placement and the final output representation. Pre-norm networks produce unnormalized outputs from the last transformer block, which is why a final layer normalization before the output projection is standard. If you are building a model where the intermediate representations are consumed by downstream components (for example, in multi-task architectures or models with auxiliary heads attached at intermediate layers), post-norm's guarantee of normalized per-block outputs can simplify design. With pre-norm, you may need to add explicit normalization at each extraction point.
Hybrid Approaches
Recent work has explored combining the benefits of both approaches. Researchers have proposed several hybrids, motivated by the desire to get pre-norm's stability alongside post-norm's normalized output guarantees.
The scaled residual approach reduces the magnitude of each sublayer's contribution before the residual addition. The idea is that large sublayer outputs are the main source of post-norm instability: if each sublayer only makes a small perturbation to the residual stream, the LayerNorm Jacobian operates on a more stable signal. The cost is slower learning in the early training phase.
One variant uses post-norm with scaled residuals:
def scaled_post_norm_block(x, sublayer_fn, gamma, beta, alpha=0.1):
"""
Scaled post-norm: reduces residual contribution for stability.
Args:
alpha: Scaling factor for sublayer output (typically 0.1-0.5)
"""
sublayer_output = sublayer_fn(x)
residual_sum = x + alpha * sublayer_output
output = layer_norm(residual_sum, gamma, beta)
return outputAnother approach, used in some recent models, applies normalization both before and after the sublayer:
def sandwich_norm_block(x, sublayer_fn, gamma1, beta1, gamma2, beta2):
"""
Sandwich normalization: LayerNorm before and after sublayer.
Provides extra stability at the cost of additional computation.
"""
# Pre-normalize
x_norm = layer_norm(x, gamma1, beta1)
# Apply sublayer
sublayer_output = sublayer_fn(x_norm)
# Post-normalize the sublayer output
sublayer_output = layer_norm(sublayer_output, gamma2, beta2)
# Add residual
output = x + sublayer_output
return outputThese hybrid approaches add complexity but can provide benefits in specific situations, particularly for extremely deep or wide networks. The sandwich norm approach has shown promise in some experimental architectures because it combines the clean inputs to the sublayer (from the pre-norm step) with the clean outputs from the sublayer (from the post-norm step), while still passing the residual through unnormalized. This gives maximum control over what the sublayer sees and produces, at the cost of two normalization operations per block. Whether the added computational cost is worth the stability benefit depends on the specific training regime and model scale.
In production systems, most practitioners default to pre-norm and tune it before considering a hybrid. Hybrids introduce additional hyperparameters, such as the alpha scaling factor, which require their own tuning. The general principle is to prefer simpler architectures unless you have a specific, well-characterized problem that a more complex design solves.
Implementation Comparison
Let's implement both variants in a clean, comparable format that highlights their differences:
class TransformerBlock:
"""
Unified transformer block supporting both pre-norm and post-norm.
"""
def __init__(self, d_model, d_ff, norm_type="pre"):
"""
Args:
d_model: Model dimension
d_ff: Feed-forward hidden dimension
norm_type: 'pre' or 'post'
"""
self.d_model = d_model
self.d_ff = d_ff
self.norm_type = norm_type
np.random.seed(42)
# Attention weights (simplified)
self.W_attn = np.random.randn(d_model, d_model) * 0.02
# Feed-forward weights
self.W1 = np.random.randn(d_model, d_ff) * 0.02
self.W2 = np.random.randn(d_ff, d_model) * 0.02
# Layer norm parameters (2 norms per block)
self.gamma1 = np.ones(d_model)
self.beta1 = np.zeros(d_model)
self.gamma2 = np.ones(d_model)
self.beta2 = np.zeros(d_model)
def attention(self, x):
"""Simplified attention (just projection for demo)."""
return x @ self.W_attn
def feed_forward(self, x):
"""Two-layer feed-forward with ReLU."""
hidden = np.maximum(0, x @ self.W1)
return hidden @ self.W2
def forward(self, x):
"""Forward pass with specified normalization strategy."""
if self.norm_type == "pre":
# Pre-norm attention
x_norm = layer_norm(x, self.gamma1, self.beta1)
x = x + self.attention(x_norm)
# Pre-norm feed-forward
x_norm = layer_norm(x, self.gamma2, self.beta2)
x = x + self.feed_forward(x_norm)
else:
# Post-norm attention
x = layer_norm(x + self.attention(x), self.gamma1, self.beta1)
# Post-norm feed-forward
x = layer_norm(x + self.feed_forward(x), self.gamma2, self.beta2)
return x# Compare forward pass behavior
np.random.seed(42)
x = np.random.randn(4, 64)
pre_block = TransformerBlock(64, 256, norm_type="pre")
post_block = TransformerBlock(64, 256, norm_type="post")
pre_output = pre_block.forward(x)
post_output = post_block.forward(x)Single Block Comparison ======================================== Input magnitude: 7.7756 Pre-norm output mag: 7.8477 Post-norm output mag: 8.0000
Even after just one block, the difference is visible. The post-norm output magnitude is close to (the expected magnitude for a normalized -dimensional vector), while pre-norm's output reflects the accumulation of the input and sublayer contributions. This difference compounds across many layers, which is why the architectural choice matters significantly for deep networks.
Limitations and Impact
The pre-norm versus post-norm choice exemplifies a common pattern in deep learning architecture design: seemingly minor structural changes can strongly affect trainability. Pre-norm solved the training stability challenges that limited early transformer scaling, directly enabling the large language models that define modern NLP.
The main limitation of pre-norm is the accumulating activation scale through the network. While the final layer normalization handles this for most purposes, it can create numerical precision challenges in extremely deep networks (hundreds of layers). Some architectures address this with periodic intermediate normalization or careful scaling of residual contributions. In practice, models with 100-plus layers using pre-norm can see activations with norms an order of magnitude larger at the final layer than at the first, which strains float16 and bfloat16 representations. This is one reason why extremely deep experimental models often use float32 for the residual stream even when computing sublayers in lower precision.
Post-norm's limitation is its training instability for deep networks. The requirement for warmup schedules and careful hyperparameter tuning increases the complexity of training pipelines. For practitioners working with pre-trained models like BERT, the post-norm design is fixed, and fine-tuning inherits these stability considerations. Fine-tuning a post-norm BERT with a learning rate that is too large will cause the same kind of instability observed during pre-training, just compressed into the fine-tuning phase. The widely-recommended fine-tuning learning rates for BERT (1e-5 to 3e-5) are much more conservative than those used for pre-norm models, partly for this reason.
The broader impact of understanding normalization placement extends beyond transformers. Similar considerations apply to any deep residual network: where you normalize relative to the residual connection fundamentally changes how gradients flow. This principle guides architecture design across computer vision, speech processing, and other domains. For practitioners building custom architectures, the lesson is to think of normalization not as a cleanup detail but as a structural choice with first-order effects on optimization dynamics.
There is also a conceptual limitation to acknowledge: the stability arguments for pre-norm come largely from empirical observation and simplified mathematical analysis. The full picture involves interactions between initialization, learning rate schedules, batch size, optimizer choice, and normalization placement that are too complex to fully characterize analytically. Pre-norm is the safer default, but if you are tuning a model and seeing unexpected instabilities, normalization placement is only one of several variables to investigate.
Key Parameters
When implementing pre-norm or post-norm transformer blocks, these parameters control the behavior and stability:
-
norm_type: Choice between"pre"or"post". Pre-norm places LayerNorm before the sublayer; post-norm places it after the residual addition. Modern large models (GPT, LLaMA) use pre-norm for stability. -
eps(LayerNorm epsilon): Small constant (typically1e-5or1e-6) added to the variance for numerical stability. Prevents division by zero when variance is very small. -
gamma,beta(LayerNorm parameters): Learnable scale and shift parameters. Initialized to ones and zeros respectively, allowing the model to learn the optimal normalization behavior for each layer. -
residual_scale: For pre-norm networks, scaling the output of sublayers by a factor like (where is the number of layers) prevents activation explosion. GPT-2 uses this technique. -
n_layers: Network depth directly impacts the choice between pre-norm and post-norm. Networks deeper than 12 layers benefit significantly from pre-norm's gradient stability. -
learning_rate: Post-norm requires smaller learning rates and warmup schedules. Pre-norm tolerates larger learning rates (often 3-10x higher) and simpler schedules.
Summary
The placement of layer normalization relative to residual connections determines whether a transformer uses pre-norm or post-norm architecture. This choice affects gradient behavior during training and the amount of tuning required.
Key takeaways from this chapter:
-
Post-norm normalizes after the residual addition: The original transformer design applies normalization to the sum of the sublayer output and residual. This ensures each layer produces normalized outputs but can create gradient flow challenges in deep networks.
-
Pre-norm normalizes before the sublayer: Moving normalization inside the residual branch provides a direct gradient path through the residual connection. This enables stable training of very deep networks without complex warmup schedules.
-
Gradient highways explain stability: The term from the residual connection in pre-norm ensures gradients can flow backward without attenuation, regardless of sublayer behavior. This mathematical property is why pre-norm trains more stably.
-
Activation accumulation is the trade-off: Pre-norm outputs are not normalized, leading to growing activation magnitudes. A final layer normalization before the output projection addresses this for most purposes.
-
Modern architectures favor pre-norm: Most large language models, including GPT and LLaMA, use pre-norm due to its stability benefits. Post-norm persists in some encoder models like BERT where network depth is more modest.
-
Learning rate tolerance differs: Pre-norm allows training with larger learning rates and simpler schedules. Post-norm requires careful warmup and learning rate selection to avoid divergence.
In the next chapter, we'll explore feed-forward networks, the other major component of transformer blocks alongside attention. Understanding how these two components work together completes the picture of transformer block architecture.
Quiz
Ready to test your understanding? Take this quick quiz to reinforce what you've learned about pre-norm and post-norm transformer architectures.
Pre-Norm vs Post-Norm
Reference
Citation details
Cite or share this article.
Continue with the full handbook
This chapter is part of Language AI Handbook. Use the handbook page to browse the complete table of contents and continue reading in sequence.
Explore Language AI HandbookStay up to date
Get articles, book updates, and news delivered to your inbox.
No spam, unsubscribe anytime.
Join the community
Sign in to remove popups, track your reading progress, and join the discussion.
Comments
No comments yet. Be the first to share your thoughts!