WritingBooksAboutCommunityContactCommunity

Search

Search articles

Memory Augmentation for Transformers: External Storage for Long Context

Michael Brenndoerfer•Updated July 8, 2025•52 min read

Learn how memory-augmented transformers extend context beyond attention limits using external key-value stores, retrieval mechanisms, and compression strategies.

Track your reading progress

Sign in to mark chapters as read and track your learning journey

Sign in →
Reading Level

Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.

Memory Augmentation

Standard transformers compress all context into a fixed-size hidden state. When processing a 100K token document, every piece of information must survive through the attention mechanism's weighted averaging. Important details from early in the document compete against recent tokens for the model's limited representational capacity. Memory augmentation offers an alternative: give the model explicit storage where it can write and retrieve information on demand.

The core insight is straightforward. Instead of forcing the model to implicitly remember everything through its weights and hidden states, we provide an external memory bank. The model can write key-value pairs to this memory during processing and query it when generating outputs. This separation of storage from computation enables effectively unlimited context while keeping each attention operation tractable.

The Memory Bottleneck in Transformers

Before diving into memory architectures, let's understand precisely why standard transformers struggle with long sequences. The problem isn't just computational cost. It's fundamental to how attention aggregates information.

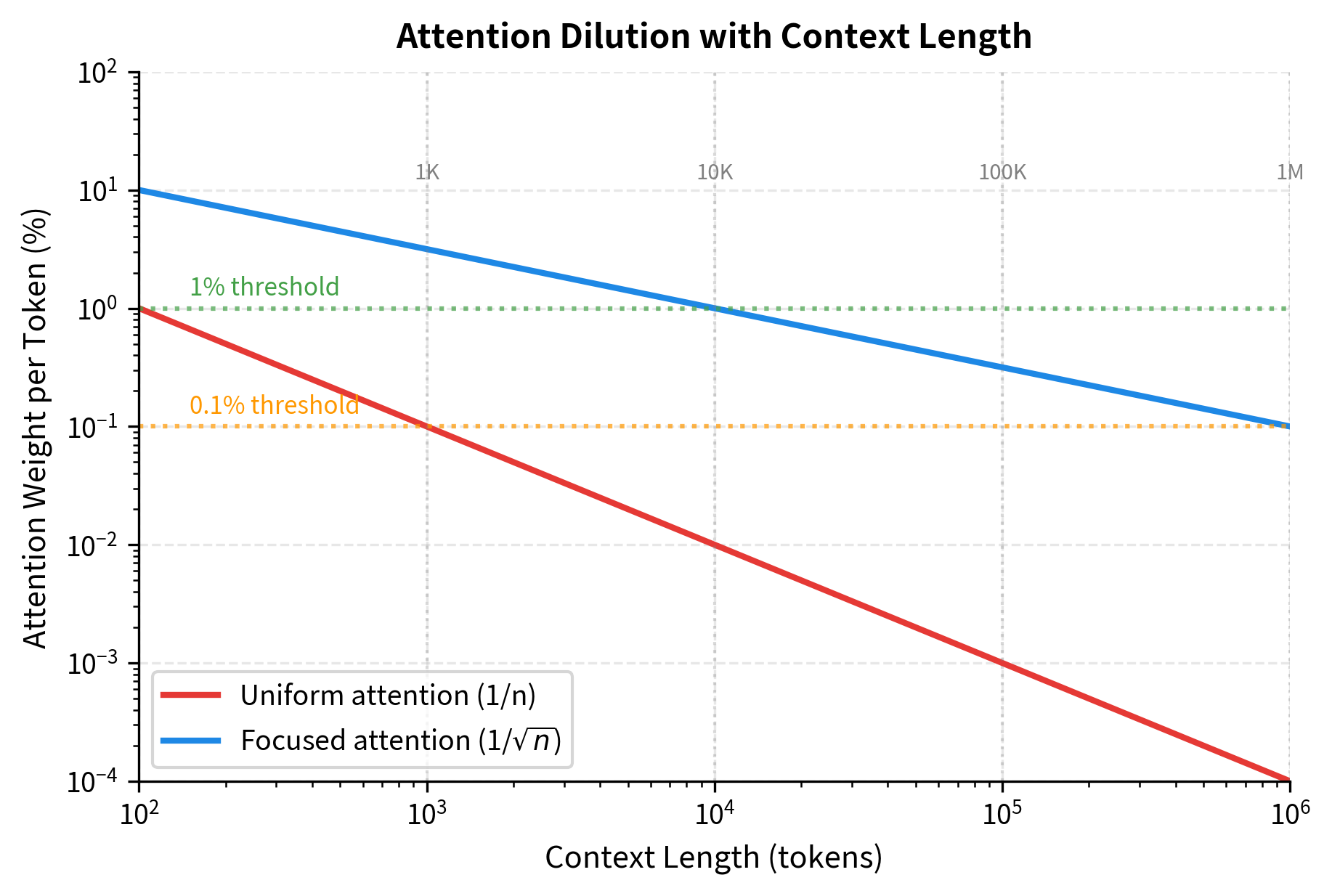
In self-attention, each token produces a query that attends over all key-value pairs from previous positions. The attention weights must sum to 1 due to softmax normalization. With a 100K token context, each previous token receives on average only 0.001% of the attention mass. If the model needs to retrieve a specific fact from 50K tokens ago, it must somehow allocate significant attention weight to that precise location while mostly ignoring the 99,999 other positions.

In[2]:
Code
import numpy as np


def attention_capacity_analysis(context_lengths, target_positions):
    """
    Analyze how attention capacity limits information retrieval.

    For a token at position t to retrieve information from position s,
    it must allocate meaningful attention weight to s among all t positions.
    """
    results = []

    for ctx_len in context_lengths:
        for target_pos in target_positions:
            if target_pos >= ctx_len:
                continue

            # Uniform attention baseline
            uniform_weight = 1.0 / ctx_len

            # Realistic "focused" attention: model learns to concentrate
            # Assume top-k attention where k = sqrt(ctx_len)
            focus_k = int(np.sqrt(ctx_len))
            focused_weight = 1.0 / focus_k if focus_k > 0 else 1.0

            # Distance from query (last position) to target
            distance = ctx_len - target_pos

            results.append(
                {
                    "context_length": ctx_len,
                    "target_position": target_pos,
                    "distance": distance,
                    "uniform_weight": uniform_weight,
                    "focused_weight": focused_weight,
                    "focus_k": focus_k,
                }
            )

    return results


context_lengths = [1000, 10000, 100000]
target_positions = [100, 1000, 10000]
capacity_results = attention_capacity_analysis(
    context_lengths, target_positions
)
Out[3]:
Console
Attention Weight Capacity Analysis:

   Context   Target Pos   Distance    Uniform %    Focused %
------------------------------------------------------------
        1K          100        900      0.1000%        3.23%
       10K          100      9,900      0.0100%        1.00%
       10K           1K      9,000      0.0100%        1.00%
      100K          100     99,900      0.0010%        0.32%
      100K           1K     99,000      0.0010%        0.32%
      100K          10K     90,000      0.0010%        0.32%

The table reveals the severity of attention dilution. With uniform attention over a 100K context, each position receives only 0.001% of the attention mass. Even with focused attention (where the model concentrates on the top n\sqrt{n} positions), each selected position only receives about 0.32% of the total weight. The longer the context, the harder it becomes to allocate sufficient attention to any single relevant position.

Out[4]:
Visualization
Log-log plot showing attention weight per token decreasing as context length increases, with two curves for uniform and focused attention.
Attention weight per token decreases rapidly as context length grows. At 100K tokens, uniform attention gives each position only 0.001% of the total weight. Even focused attention (attending to top √n positions) provides only ~0.3% per selected position, making precise information retrieval increasingly difficult.

Even with focused attention, retrieving information from a 100K context requires the model to correctly select that position from among approximately 316 candidate slots. This number comes from the square root of the context length: 100,000≈316\sqrt{100{,}000} \approx 316. If the model can only meaningfully attend to the top n\sqrt{n} positions (where nn is the context length), then it must route attention to the right location among those 316 candidates without knowing in advance where relevant information lies.

Memory Bottleneck

The memory bottleneck in transformers refers to the fundamental tension between context length and information retrieval precision. As context grows, attention becomes increasingly diluted, making it harder to retrieve specific information from distant positions. Memory augmentation addresses this by providing explicit storage separate from the attention mechanism.

Memory-augmented architectures sidestep this bottleneck by decoupling storage from the attention computation. The model can write important information to memory during one pass and retrieve it precisely during another, without competing for attention mass against the entire context.

Memory Network Fundamentals

Imagine you're reading a 500-page novel and someone asks you, "What color was the protagonist's childhood home?" You don't re-read the entire book. Instead, your mind somehow retrieves that specific detail from storage. Memory networks attempt to give neural networks this same capability: the ability to write information to an external store during processing and retrieve it on demand.

The Key Insight: Separate Storage from Computation

The fundamental innovation of memory networks is decoupling what the model remembers from how it processes information. In a standard neural network, "memory" exists implicitly in the hidden states, and information must survive through layer after layer of transformation. In a memory network, we provide an explicit storage mechanism that the model can query independently.

This separation immediately suggests two operations:

  1. Writing: The model encounters important information and stores it
  2. Reading: The model needs information and retrieves it from storage

But how should storage be organized? And how does the model know where to look when reading?

Content-Based Addressing: Finding Information by What It Contains

Consider how you might organize a library. You could assign each book a numbered shelf (positional addressing), or you could organize books by topic and keywords (content-based addressing). A positional system requires remembering exactly where you put each book. A content-based system lets you find books by describing what you're looking for.

Memory networks use content-based addressing. Each memory entry consists of two parts:

  • A key ki\mathbf{k}_i: describes what the entry contains (like a book's title and keywords)
  • A value vi\mathbf{v}_i: the actual stored content (like the book itself)

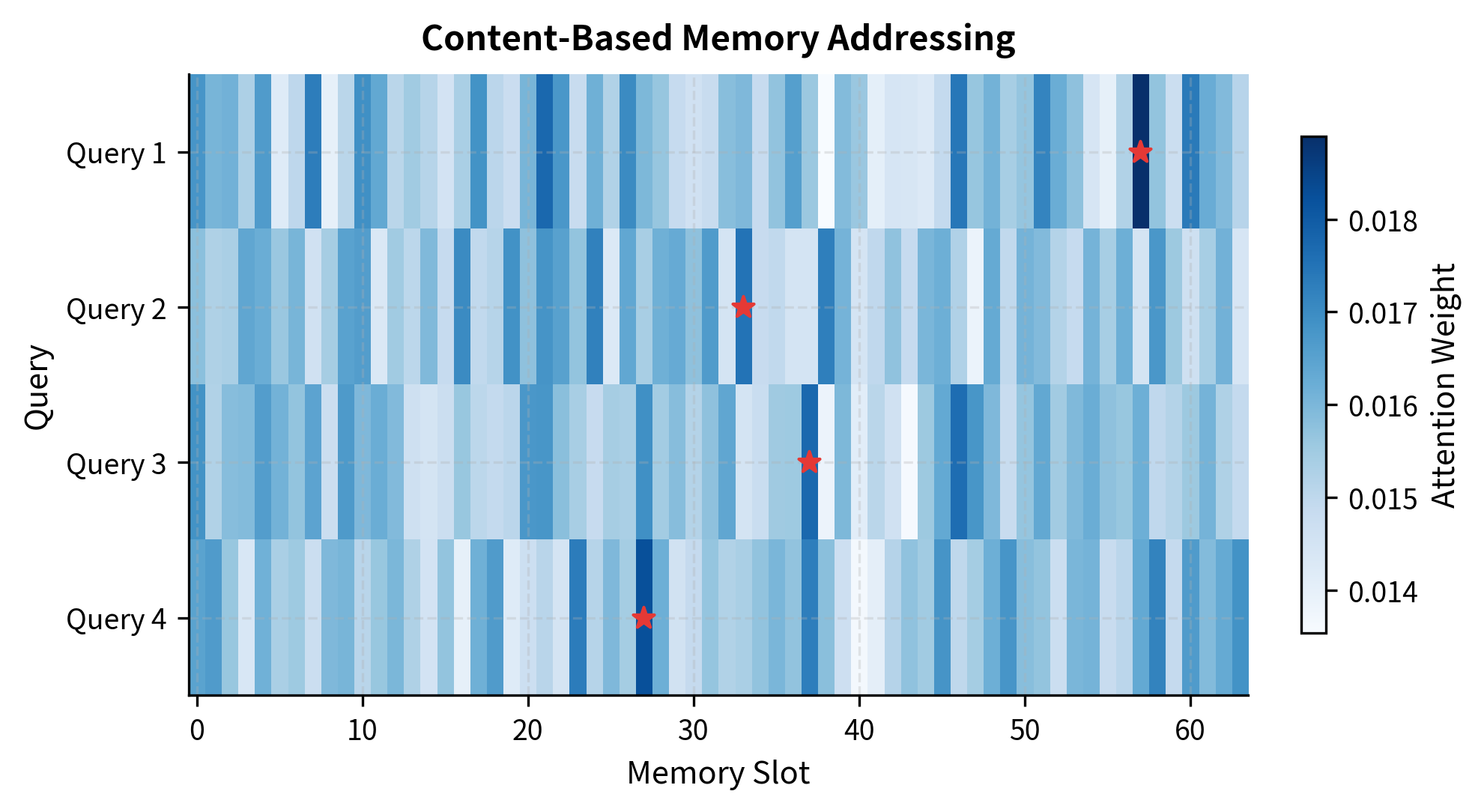
When the model wants to retrieve information, it provides a query q\mathbf{q} describing what it's looking for. The memory system compares this query against all stored keys and returns the values whose keys match best.

The Mathematics of Matching: Similarity and Softmax

How do we measure whether a query matches a key? The most natural choice is the dot product. Given a query vector q\mathbf{q} and a key vector ki\mathbf{k}_i, their similarity is:

si=q⋅ki=∑j=1dqj⋅kijs_i = \mathbf{q} \cdot \mathbf{k}_i = \sum_{j=1}^{d} q_j \cdot k_{ij}

where:

  • q∈Rd\mathbf{q} \in \mathbb{R}^d is the query vector with dimension dd
  • ki∈Rd\mathbf{k}_i \in \mathbb{R}^d is the key for memory slot ii
  • sis_i is the scalar similarity score

This score tells us how well the query aligns with each key. Larger positive values indicate better matches. But we need to convert these raw scores into a probability distribution, a set of weights that sum to 1, telling us how much to trust each memory entry.

The softmax function accomplishes this. For nn memory slots with similarity scores s1,…,sns_1, \ldots, s_n:

αi=esi∑j=1nesj\alpha_i = \frac{e^{s_i}}{\sum_{j=1}^{n} e^{s_j}}

The exponential esie^{s_i} ensures all weights are positive (since ex>0e^x > 0 for all xx). The denominator normalizes so that ∑iαi=1\sum_i \alpha_i = 1. The weight αi\alpha_i can be interpreted as "the probability that memory slot ii contains what we're looking for."

Scaling for Stable Gradients

In practice, we add one refinement. When the dimension dd is large, dot products can become very large in magnitude. This pushes softmax outputs toward extreme values (nearly 0 or nearly 1), which causes gradient problems during training. The solution is scaled dot-product attention:

si=q⋅kids_i = \frac{\mathbf{q} \cdot \mathbf{k}_i}{\sqrt{d}}

Why d\sqrt{d}? If each component of q\mathbf{q} and k\mathbf{k} has variance 1, then the dot product has variance dd (since we're summing dd independent products). Dividing by d\sqrt{d} restores unit variance, keeping the scores in a well-behaved range regardless of dimension.

Retrieving the Answer: Weighted Combination

Once we have attention weights αi\alpha_i over all memory slots, we retrieve information by taking a weighted sum of the stored values:

r=∑i=1nαi⋅vi\mathbf{r} = \sum_{i=1}^{n} \alpha_i \cdot \mathbf{v}_i

where:

  • r∈Rdv\mathbf{r} \in \mathbb{R}^{d_v} is the retrieved vector (output)
  • vi∈Rdv\mathbf{v}_i \in \mathbb{R}^{d_v} is the value stored in memory slot ii
  • αi\alpha_i is the attention weight computed above

This weighted sum is fully differentiable, meaning gradients can flow back through the retrieval operation during training. The model learns which keys to associate with which values by receiving gradient signals about whether the retrieved information helped with the task.

Putting It Together: The Complete Memory Read

The full memory read operation combines all these steps:

r=MemoryRead(q,K,V)=∑i=1nsoftmax(qKTd)i⋅vi\mathbf{r} = \text{MemoryRead}(\mathbf{q}, \mathbf{K}, \mathbf{V}) = \sum_{i=1}^{n} \text{softmax}\left(\frac{\mathbf{q} \mathbf{K}^T}{\sqrt{d}}\right)_i \cdot \mathbf{v}_i

where:

  • K∈Rn×d\mathbf{K} \in \mathbb{R}^{n \times d} is the matrix of all nn keys stacked as rows
  • V∈Rn×dv\mathbf{V} \in \mathbb{R}^{n \times d_v} is the matrix of all nn values stacked as rows
  • qKT\mathbf{q} \mathbf{K}^T computes all nn similarity scores in parallel

This is identical to the attention mechanism used in transformers. The difference is conceptual: in standard self-attention, keys and values come from the input sequence; in a memory network, they come from an external storage that persists across inputs.

Implementation: A Basic Memory Network

Let's translate these mathematical concepts into working code. The implementation directly mirrors the formulas above:

In[5]:
Code
import torch
import torch.nn as nn
import torch.nn.functional as F


class BasicMemoryNetwork(nn.Module):
    """
    A basic memory network demonstrating core memory operations.

    The memory stores key-value pairs. Reading uses content-based
    attention over keys to retrieve values. Writing adds new entries.
    """

    def __init__(self, memory_size, key_dim, value_dim):
        super().__init__()
        self.memory_size = memory_size
        self.key_dim = key_dim
        self.value_dim = value_dim

        # Initialize memory as learnable parameters
        # K ∈ R^(n × d): matrix of n keys, each with dimension d
        self.memory_keys = nn.Parameter(torch.randn(memory_size, key_dim) * 0.1)
        # V ∈ R^(n × d_v): matrix of n values, each with dimension d_v
        self.memory_values = nn.Parameter(
            torch.randn(memory_size, value_dim) * 0.1
        )

        # Query projection: transforms raw query into key space
        self.query_proj = nn.Linear(key_dim, key_dim)

    def read(self, query):
        """
        Read from memory using content-based attention.

        This implements: r = Σ_i softmax(q·K^T / √d)_i · v_i

        Args:
            query: (batch, key_dim) - what we're looking for

        Returns:
            retrieved: (batch, value_dim) - weighted sum of memory values
            attention: (batch, memory_size) - attention weights α over memory
        """
        # Project query into key space
        query = self.query_proj(query)

        # Step 1: Compute similarity scores s_i = q · k_i for all keys
        # Matrix form: scores = q @ K^T gives all n scores at once
        scores = torch.matmul(query, self.memory_keys.T)  # (batch, n)

        # Step 2: Scale by √d for numerical stability
        scores = scores / np.sqrt(self.key_dim)

        # Step 3: Convert to attention weights α_i via softmax
        attention = F.softmax(scores, dim=-1)  # (batch, n), sums to 1

        # Step 4: Retrieve weighted sum r = Σ_i α_i · v_i
        retrieved = torch.matmul(attention, self.memory_values)  # (batch, d_v)

        return retrieved, attention

    def forward(self, query):
        return self.read(query)
In[6]:
Code
# Demonstrate basic memory operations
torch.manual_seed(42)

memory_net = BasicMemoryNetwork(memory_size=64, key_dim=128, value_dim=256)

# Create a batch of queries
batch_size = 4
queries = torch.randn(batch_size, 128)

# Read from memory
retrieved_values, attention_weights = memory_net(queries)
Out[7]:
Console
Basic Memory Network Demonstration:
  Memory size: 64 slots
  Key dimension: 128
  Value dimension: 256

Query batch shape: torch.Size([4, 128])
Retrieved values shape: torch.Size([4, 256])
Attention weights shape: torch.Size([4, 64])

Attention statistics (first query):
  Top-5 slots: [57, 21, 46, 60, 7]
  Top-5 weights: ['0.019', '0.018', '0.017', '0.017', '0.017']
  Sum of top-5: 0.089

The output reveals how attention weights distribute across memory slots. Even with random initialization (where keys and queries have no learned relationship), the softmax produces a sparse pattern. The top 5 slots capture a significant fraction of total attention mass, demonstrating the inherent focusing behavior of the exponential function. After training, these weights would reflect genuine content similarity, with the model having learned to store related information under similar keys.

Out[8]:
Visualization
Heatmap with 4 rows (queries) and 64 columns (memory slots), showing sparse attention patterns with each query attending to different slots.
Attention weight heatmap for 4 queries over 64 memory slots. Each row shows one query's attention distribution. Darker cells indicate higher attention weights. Note how each query focuses on different memory locations, demonstrating content-based addressing.

Memory Retrieval Mechanisms: From Soft to Efficient

The basic memory read operation we just implemented has an elegant mathematical formulation, but it harbors a serious scalability problem. Let's understand this issue deeply before exploring solutions.

The Soft Attention Baseline

Our memory read computes attention over all memory slots:

αi=softmax(q⋅kid)for i=1,…,n\alpha_i = \text{softmax}\left(\frac{\mathbf{q} \cdot \mathbf{k}_i}{\sqrt{d}}\right) \quad \text{for } i = 1, \ldots, n

This soft attention approach has an important advantage: it's fully differentiable. Gradients flow smoothly from the output through the softmax and into the query and key representations. The model can learn what to store and how to query through standard backpropagation.

But soft attention also inherits the same dilution problem we identified earlier for long-context transformers. When nn is large, each slot's weight αi\alpha_i becomes vanishingly small. The information we need gets drowned in a weighted average dominated by irrelevant entries.

Temperature: Controlling the Focus-Diffusion Tradeoff

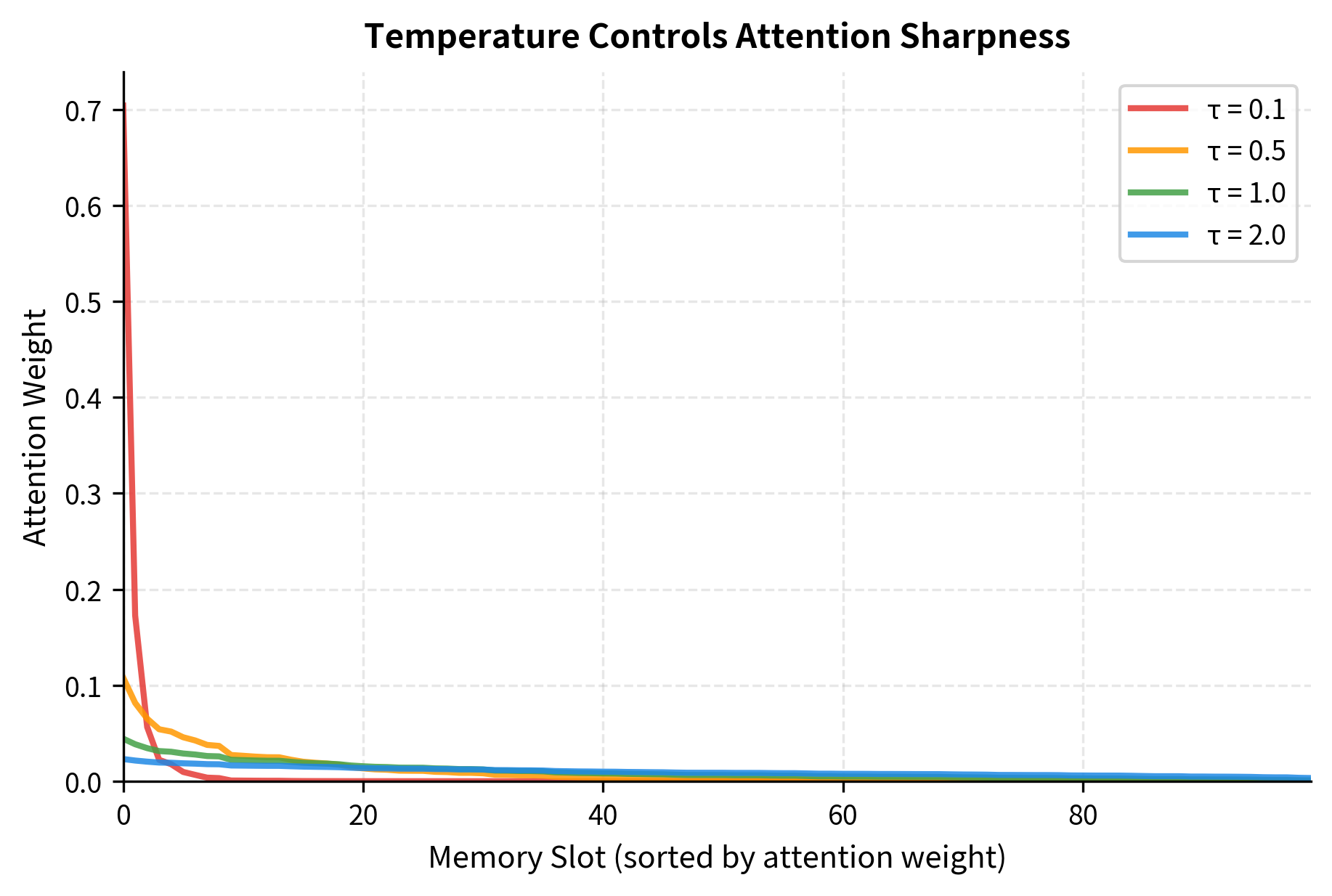
One way to combat dilution is to sharpen the attention distribution. We can introduce a temperature parameter τ\tau that scales the scores before softmax:

αi=softmax(q⋅kid⋅τ)\alpha_i = \text{softmax}\left(\frac{\mathbf{q} \cdot \mathbf{k}_i}{\sqrt{d} \cdot \tau}\right)

The temperature τ\tau controls the "peakiness" of the distribution:

  • Low temperature (τ<1\tau < 1): Amplifies score differences. Small advantages become large, concentrating attention on the best-matching entries. In the limit τ→0\tau \to 0, this approaches hard argmax selection.

  • High temperature (τ>1\tau > 1): Dampens score differences. The distribution becomes more uniform, spreading attention across many entries.

We can measure this effect through entropy, which quantifies how spread out a distribution is:

H(α)=−∑i=1nαilog⁡αiH(\alpha) = -\sum_{i=1}^{n} \alpha_i \log \alpha_i

Low entropy means attention is concentrated on few slots; high entropy means it's spread across many.

In[9]:
Code
def soft_attention_retrieval(
    query, memory_keys, memory_values, temperature=1.0
):
    """
    Retrieve from memory using soft attention with temperature scaling.

    The temperature τ controls focus vs diffusion:
    - τ < 1: More focused (approaches hard selection)
    - τ = 1: Standard softmax
    - τ > 1: More diffuse (approaches uniform)

    Args:
        query: (batch, dim)
        memory_keys: (memory_size, dim)
        memory_values: (memory_size, value_dim)
        temperature: Scaling factor τ for attention sharpness

    Returns:
        retrieved: (batch, value_dim)
        attention: (batch, memory_size)
    """
    # Compute scaled similarities: s_i / (√d · τ)
    scores = torch.matmul(query, memory_keys.T)  # (batch, memory_size)
    scores = scores / (np.sqrt(query.shape[-1]) * temperature)

    # Soft attention weights: α_i = softmax(scores)_i
    attention = F.softmax(scores, dim=-1)

    # Weighted retrieval: r = Σ_i α_i · v_i
    retrieved = torch.matmul(attention, memory_values)

    return retrieved, attention


# Compare different temperatures
temperatures = [0.1, 0.5, 1.0, 2.0]
query = torch.randn(1, 128)
keys = torch.randn(100, 128)
values = torch.randn(100, 64)

temperature_results = []
for temp in temperatures:
    _, attn = soft_attention_retrieval(query, keys, values, temperature=temp)
    # Compute entropy: H(α) = -Σ α_i log(α_i)
    entropy = -torch.sum(attn * torch.log(attn + 1e-10), dim=-1).item()
    max_weight = attn.max().item()
    temperature_results.append(
        {"temperature": temp, "entropy": entropy, "max_weight": max_weight}
    )
Out[10]:
Console
Temperature Effect on Retrieval Sharpness:

 Temperature      Entropy   Max Weight            Interpretation
-----------------------------------------------------------------
         0.1        0.515        0.877  Very focused (near hard)
         0.5        3.313        0.179                   Focused
         1.0        4.210        0.061                  Standard
         2.0        4.500        0.027                   Diffuse
Out[11]:
Visualization
Four line plots showing attention weight distributions, from highly peaked at low temperature to more uniform at high temperature.
Attention weight distributions over 100 memory slots at different temperatures. Low temperature (τ=0.1) concentrates nearly all weight on one slot. High temperature (τ=2.0) spreads weight more uniformly, enabling information aggregation from multiple sources.

The results demonstrate the entropy-focus tradeoff concretely. At temperature 0.1, the entropy is low and the maximum weight approaches 1.0, meaning the model concentrates almost all attention on a single memory slot. The softmax has become nearly a hard argmax. At temperature 2.0, entropy increases substantially as attention spreads more evenly across slots.

This tradeoff has practical implications:

  • For fact retrieval (e.g., "What is the capital of France?"), use low temperatures. The answer exists in one specific memory location.
  • For synthesis tasks (e.g., "Summarize the key themes"), use higher temperatures. Relevant information is distributed across many entries.
  • For training, moderate temperatures (0.5-1.0) often work best. They allow gradient flow to multiple entries without completely diluting the signal.

However, temperature alone cannot solve the scalability problem. Even with sharp attention, we still compute similarities with all nn memory entries. When nn reaches millions, this becomes prohibitively expensive.

Top-k Retrieval: Trading Differentiability for Efficiency

A more radical solution abandons the soft attention over all entries. Instead, we first find the kk most relevant memory slots using a discrete selection step, then apply soft attention only over those kk entries:

Top-k(s)={i1,i2,…,ik}where si1≥si2≥⋯≥sik\text{Top-}k(\mathbf{s}) = \{i_1, i_2, \ldots, i_k\} \quad \text{where } s_{i_1} \geq s_{i_2} \geq \cdots \geq s_{i_k}

The top-kk operation returns the indices of the kk highest-scoring entries. We then compute attention only over this subset:

αj=softmax(sij)for j=1,…,k\alpha_j = \text{softmax}(s_{i_j}) \quad \text{for } j = 1, \ldots, k r=∑j=1kαj⋅vij\mathbf{r} = \sum_{j=1}^{k} \alpha_j \cdot \mathbf{v}_{i_j}

The key insight is that kk is fixed regardless of memory size nn. Whether the memory contains 1,000 or 1,000,000 entries, we only attend over kk slots in the final step. This bounds the attention computation at O(k)O(k) regardless of nn.

The Differentiability Tradeoff

There's a catch: the top-kk selection involves an argmax-like operation (finding the highest scores), which is not differentiable. During backpropagation, we cannot compute gradients through the discrete selection step.

This means entries that weren't selected receive no gradient signal, even if they were "almost" selected. The model cannot learn to make a near-miss entry more relevant. In practice, this limitation is often acceptable because:

  1. The entries that were selected still receive full gradients
  2. The key representations are typically trained with other objectives (like the main language modeling loss)
  3. The selection step can be approximated during training using straight-through estimators or Gumbel-softmax tricks

For many applications, the efficiency gains vastly outweigh this differentiability cost.

In[12]:
Code
def topk_retrieval(query, memory_keys, memory_values, k=10):
    """
    Retrieve from memory using top-k selection followed by soft attention.

    This is a two-stage process:
    1. Find the k keys with highest similarity to the query (discrete)
    2. Apply softmax attention over only those k entries (continuous)

    Complexity: O(n) for scoring + O(k) for attention = O(n) total
    but the attention step is bounded by k regardless of n
    """
    # Stage 1: Compute all n similarity scores
    scores = torch.matmul(query, memory_keys.T)  # (batch, n)
    scores = scores / np.sqrt(query.shape[-1])

    # Stage 2: Select top-k (discrete, non-differentiable)
    topk_scores, topk_indices = torch.topk(scores, k, dim=-1)

    # Gather the k corresponding values
    batch_size = query.shape[0]
    topk_values = memory_values[topk_indices.view(-1)].view(batch_size, k, -1)

    # Stage 3: Soft attention over just the k entries
    topk_attention = F.softmax(topk_scores, dim=-1)  # (batch, k)

    # Weighted sum over k entries (not n!)
    retrieved = torch.einsum("bk,bkd->bd", topk_attention, topk_values)

    return retrieved, topk_indices, topk_attention


# Demonstrate top-k retrieval on a large memory
torch.manual_seed(42)
memory_size = 10000
query = torch.randn(4, 128)
large_keys = torch.randn(memory_size, 128)
large_values = torch.randn(memory_size, 64)

for k in [5, 20, 100]:
    retrieved, indices, attn = topk_retrieval(
        query, large_keys, large_values, k=k
    )
Out[13]:
Console
Top-k Retrieval from 10,000 Memory Slots:

     k   Compute Ratio    Memory Slots Used
---------------------------------------------
     5           0.05%                    5
    20           0.20%                   20
   100           1.00%                  100

The efficiency gains are dramatic. With k=5k=5, we use only 0.05% of the memory slots for the attention computation, a 2000x reduction compared to attending to all entries. Even with k=100k=100 for more comprehensive retrieval, we still use only 1% of the memory.

Complexity Analysis: Where the Time Goes

Let's trace through the computational costs:

  1. Scoring all keys: We still compute q⋅ki\mathbf{q} \cdot \mathbf{k}_i for all nn entries: O(n⋅d)O(n \cdot d)
  2. Finding top-k: Selecting the kk largest from nn scores: O(n)O(n) (or O(nlog⁡k)O(n \log k) for a heap-based algorithm)
  3. Attention over k: Softmax and weighted sum over kk entries: O(k⋅dv)O(k \cdot d_v)

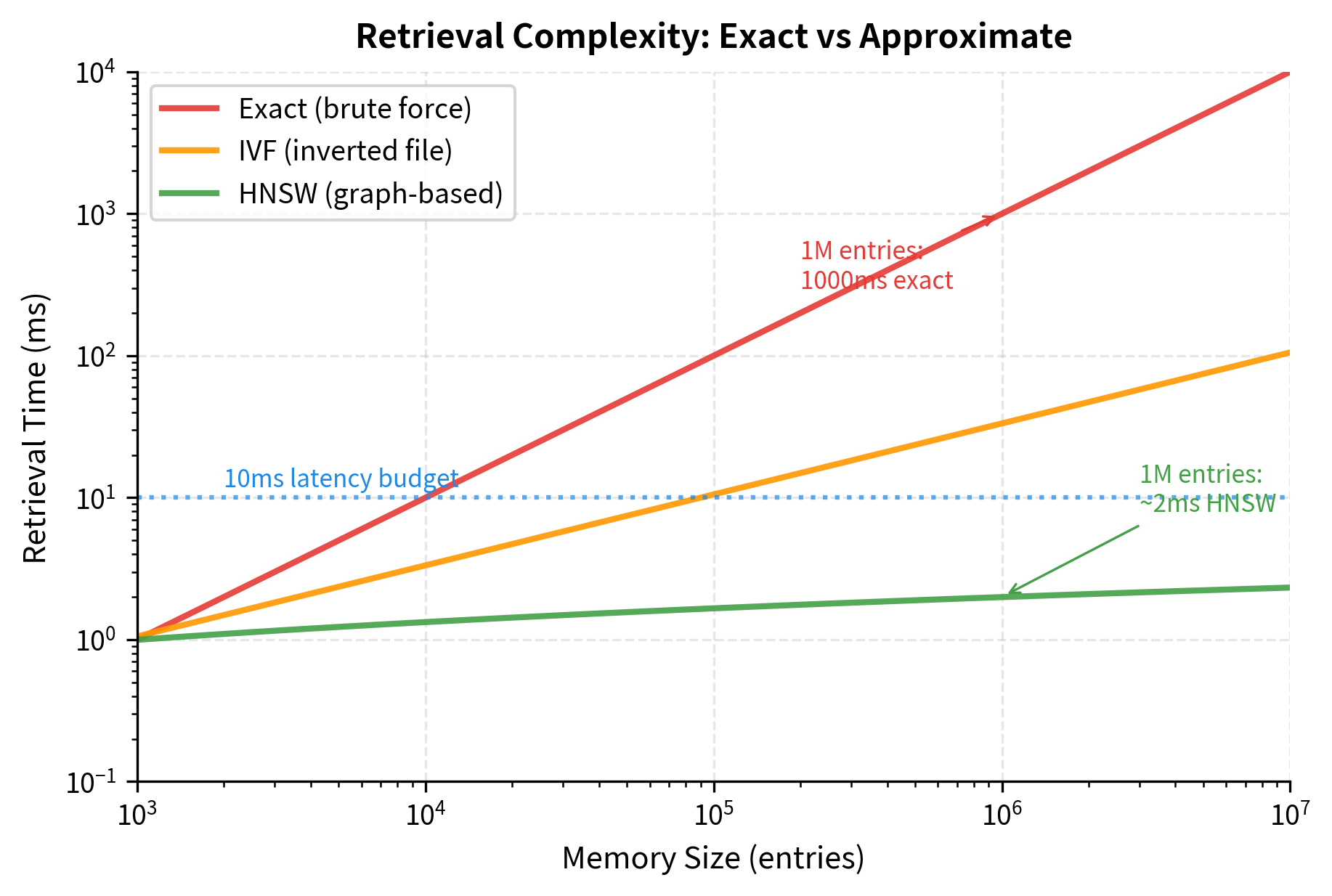
The total is O(n⋅d)O(n \cdot d) for exact top-k retrieval. We've bounded the attention step but not the scoring step.

For truly large memories (millions of entries), even linear scoring becomes prohibitive. This is where approximate nearest neighbor (ANN) algorithms enter. Methods like FAISS, ScaNN, or Annoy build index structures that support sublinear retrieval:

  • Exact search: O(n)O(n) to find top-k
  • Approximate search: O(log⁡n)O(\log n) or even O(1)O(1) depending on the algorithm and acceptable accuracy loss

With ANN indexing, a memory of 1 million entries can be queried nearly as fast as a memory of 1,000 entries, at the cost of occasionally missing the truly best match.

Out[14]:
Visualization
Log-log plot comparing retrieval time vs memory size for exact, HNSW, and IVF search methods.
Retrieval time scaling for different algorithms. Exact search grows linearly with memory size, becoming impractical for millions of entries. Approximate methods (HNSW, IVF) achieve sub-linear scaling, making million-scale memories feasible.

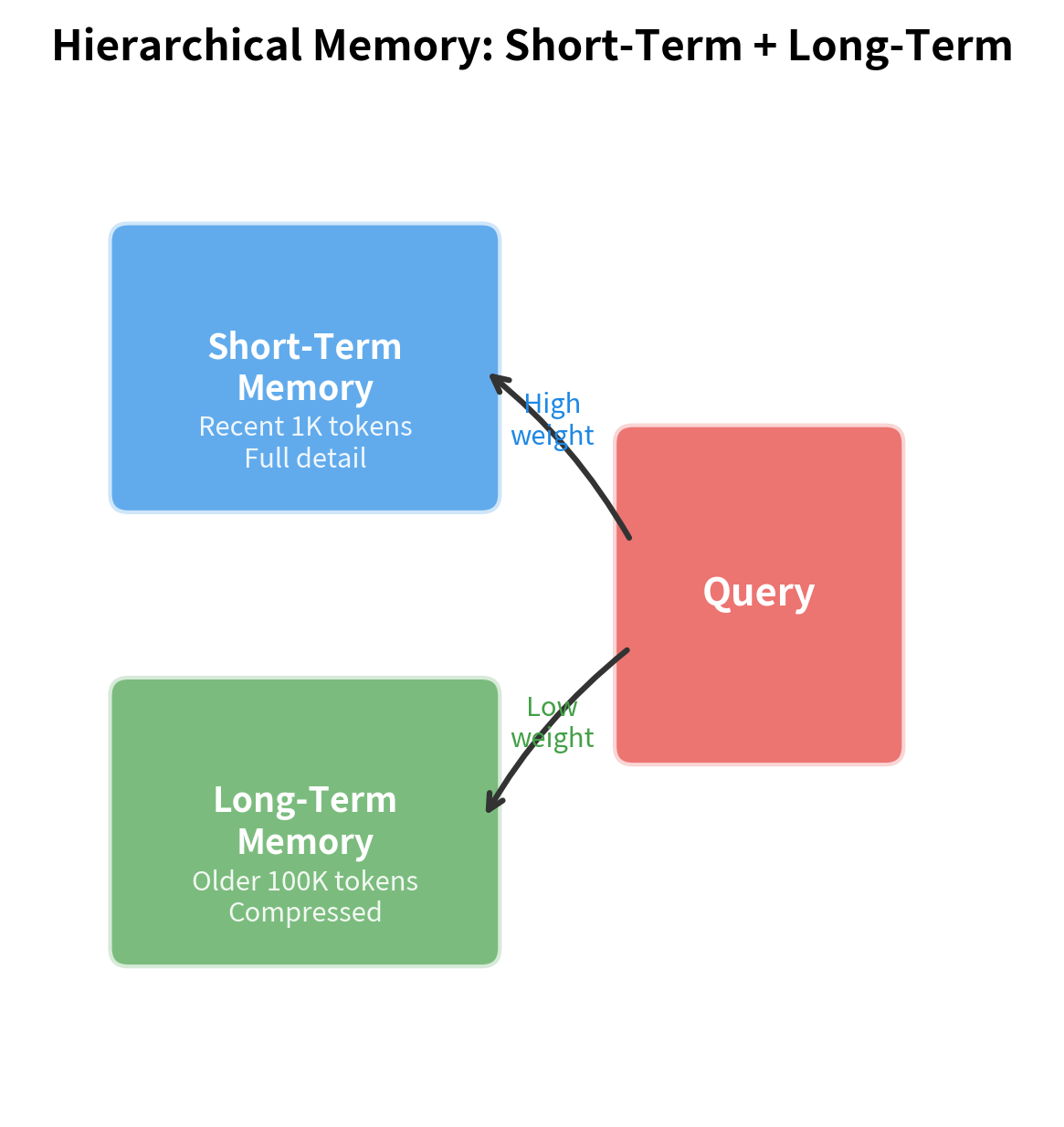
Hierarchical Memory

Top-k retrieval solves the attention efficiency problem but treats all memory entries uniformly. When memories span multiple time scales, a more sophisticated organization helps: hierarchical memory separates recent detailed information from older compressed summaries.

Short-term memory holds recent context at full resolution, while long-term memory stores condensed representations from earlier. The model queries both levels, using short-term memory for detailed recent information and long-term memory for general patterns.

Out[15]:
Visualization
Diagram showing two rectangular memory banks stacked vertically, with arrows from a query box pointing to both levels.
Hierarchical memory organization with two levels. Short-term memory (top) holds detailed recent information with high-resolution keys. Long-term memory (bottom) stores compressed summaries from earlier context. Queries attend to both levels with different weightings.

The hierarchical approach mirrors how human memory works: detailed episodic memory for recent events, condensed semantic memory for older knowledge. For language models, this translates to storing recent token representations at full resolution while compressing older context into summary vectors.

Memory Writing and Updating

Reading is only half the story. The model must also decide what to write to memory and when to update existing entries. Several strategies exist.

Append-Only Memory

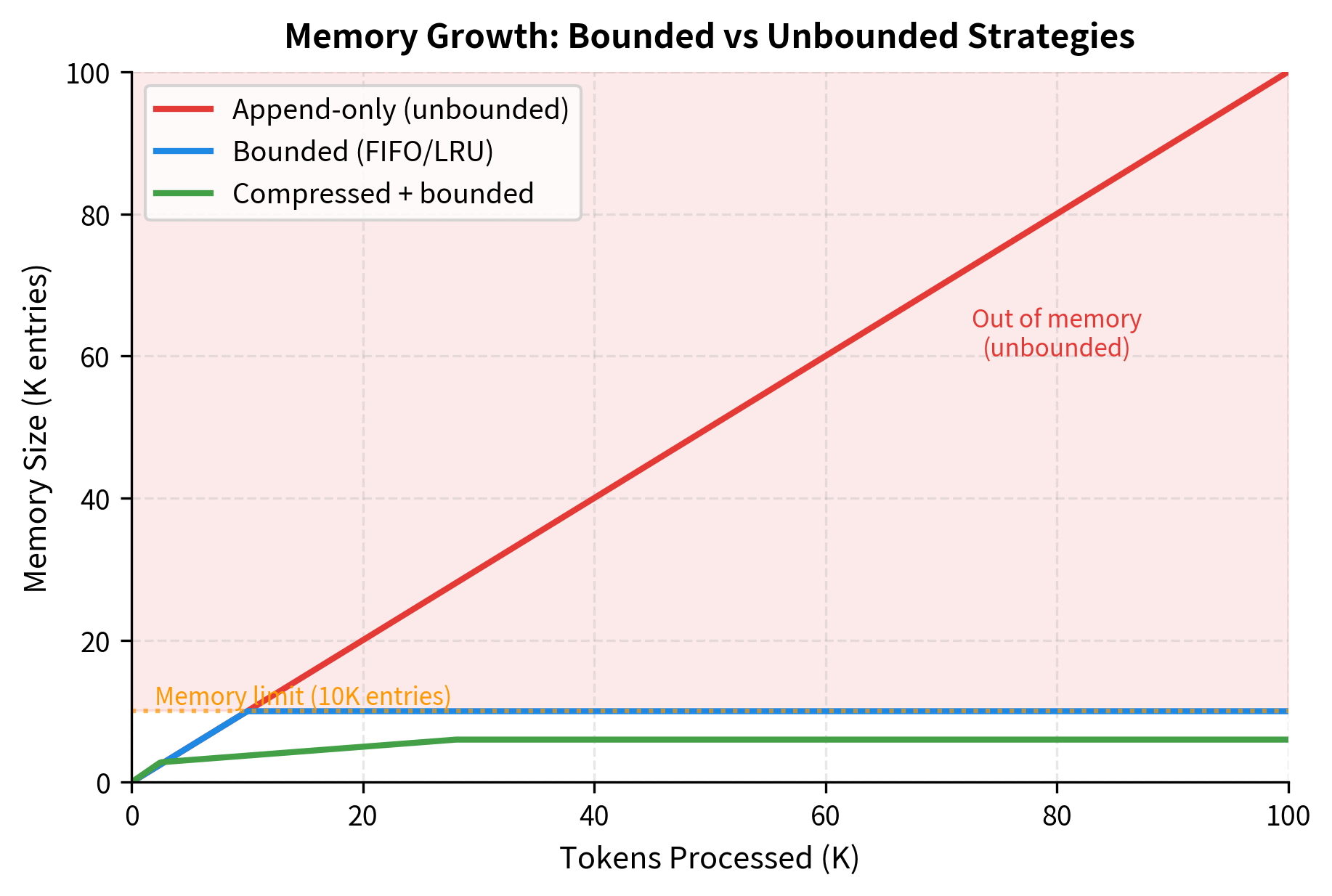
The simplest approach appends new key-value pairs without modifying existing entries. This preserves all historical information but causes unbounded memory growth.

In[16]:
Code
class AppendOnlyMemory:
    """
    Memory that grows by appending new entries.
    Simple but unbounded in size.
    """

    def __init__(self, key_dim, value_dim):
        self.key_dim = key_dim
        self.value_dim = value_dim
        self.keys = []
        self.values = []

    def write(self, key, value):
        """Add a new entry to memory."""
        self.keys.append(key)
        self.values.append(value)

    def read(self, query, k=10):
        """Read from memory using top-k retrieval."""
        if not self.keys:
            return None, None

        keys_tensor = torch.stack(self.keys)
        values_tensor = torch.stack(self.values)

        # Compute similarities
        scores = torch.matmul(query, keys_tensor.T)
        k = min(k, len(self.keys))
        topk_scores, topk_indices = torch.topk(scores.squeeze(), k)

        # Retrieve
        topk_values = values_tensor[topk_indices]
        attention = F.softmax(topk_scores, dim=-1)
        retrieved = torch.sum(attention.unsqueeze(-1) * topk_values, dim=0)

        return retrieved, topk_indices

    def size(self):
        return len(self.keys)


# Simulate memory growth
memory = AppendOnlyMemory(key_dim=64, value_dim=128)
tokens_processed = [100, 500, 1000, 5000, 10000]

for n in tokens_processed:
    # Simulate adding entries
    for _ in range(n - memory.size()):
        key = torch.randn(64)
        value = torch.randn(128)
        memory.write(key, value)
Out[17]:
Console
Append-Only Memory Growth:

  Tokens Processed     Memory Size  Memory (MB, est.)
-------------------------------------------------------
               100             100              0.07
               500             500              0.37
             1,000           1,000              0.73
             5,000           5,000              3.66
            10,000          10,000              7.32

Memory usage grows linearly with tokens processed. After processing 10,000 tokens, the memory consumes approximately 0.73 MB. While this seems manageable, extrapolating to 1 million tokens would require 73 MB, and to 100 million tokens would require 7.3 GB. For long-running applications like continuous conversation or document streaming, this unbounded growth eventually exhausts available memory.

Out[18]:
Visualization
Line plot comparing memory size growth over tokens processed for append-only, FIFO, and LRU strategies.
Memory consumption over time for different storage strategies. Append-only grows without bound, eventually exhausting resources. Bounded strategies (FIFO, LRU) plateau at the configured limit, enabling indefinite processing at fixed memory cost.

Bounded Memory with Eviction

To bound memory size, older or less-used entries must be evicted. Common strategies include FIFO (first-in, first-out), LRU (least recently used), and importance-weighted eviction.

In[19]:
Code
class BoundedMemory:
    """
    Memory with fixed maximum size.
    Evicts entries when capacity is reached.
    """

    def __init__(self, max_size, key_dim, value_dim, eviction="fifo"):
        self.max_size = max_size
        self.key_dim = key_dim
        self.value_dim = value_dim
        self.eviction = eviction

        # Storage
        self.keys = torch.zeros(max_size, key_dim)
        self.values = torch.zeros(max_size, value_dim)
        self.write_ptr = 0
        self.filled = 0

        # For LRU tracking
        self.access_times = torch.zeros(max_size)
        self.current_time = 0

    def write(self, key, value):
        """Write to memory, evicting if necessary."""
        if self.eviction == "fifo":
            # Write at current pointer, wrapping around
            idx = self.write_ptr
            self.write_ptr = (self.write_ptr + 1) % self.max_size
        elif self.eviction == "lru":
            if self.filled < self.max_size:
                idx = self.filled
            else:
                # Find least recently accessed
                idx = torch.argmin(self.access_times[: self.filled]).item()
        else:
            raise ValueError(f"Unknown eviction policy: {self.eviction}")

        self.keys[idx] = key
        self.values[idx] = value
        self.filled = min(self.filled + 1, self.max_size)
        self.access_times[idx] = self.current_time
        self.current_time += 1

    def read(self, query, k=10):
        """Read with top-k retrieval, updating access times for LRU."""
        if self.filled == 0:
            return None, None

        active_keys = self.keys[: self.filled]
        active_values = self.values[: self.filled]

        scores = torch.matmul(query, active_keys.T)
        k = min(k, self.filled)
        topk_scores, topk_indices = torch.topk(scores.squeeze(), k)

        # Update access times for LRU
        self.access_times[topk_indices] = self.current_time
        self.current_time += 1

        topk_values = active_values[topk_indices]
        attention = F.softmax(topk_scores, dim=-1)
        retrieved = torch.sum(attention.unsqueeze(-1) * topk_values, dim=0)

        return retrieved, topk_indices


# Compare eviction policies
fifo_mem = BoundedMemory(
    max_size=100, key_dim=64, value_dim=128, eviction="fifo"
)
lru_mem = BoundedMemory(max_size=100, key_dim=64, value_dim=128, eviction="lru")
Out[20]:
Console
Bounded Memory with Different Eviction Policies:

Maximum size: 100 slots

FIFO (First-In, First-Out):
  - Evicts oldest entries regardless of usage
  - Simple, predictable behavior
  - Good when all information has equal importance

LRU (Least Recently Used):
  - Evicts entries not accessed recently
  - Keeps frequently-needed information
  - Better for repeated retrieval patterns

The choice of eviction policy depends on the access patterns of your application. FIFO works well when information has a natural temporal ordering and older entries become less relevant over time. LRU is better suited for applications with "hot" entries that are accessed repeatedly, as it keeps frequently-used information available even if it was written long ago.

Learnable Writing Decisions

More sophisticated approaches learn when and what to write. A gating mechanism can control write operations based on content importance.

In[21]:
Code
class GatedMemoryWriter(nn.Module):
    """
    Learns to gate write operations based on content importance.

    A write gate determines whether new content should be stored.
    This prevents memory from filling with redundant information.
    """

    def __init__(self, input_dim, key_dim, value_dim, memory_size):
        super().__init__()
        self.memory_size = memory_size

        # Projections for key and value
        self.key_proj = nn.Linear(input_dim, key_dim)
        self.value_proj = nn.Linear(input_dim, value_dim)

        # Write gate: determines importance
        self.write_gate = nn.Sequential(
            nn.Linear(input_dim, 64), nn.ReLU(), nn.Linear(64, 1), nn.Sigmoid()
        )

        # Memory storage
        self.keys = nn.Parameter(
            torch.zeros(memory_size, key_dim), requires_grad=False
        )
        self.values = nn.Parameter(
            torch.zeros(memory_size, value_dim), requires_grad=False
        )
        self.write_ptr = 0

    def forward(self, x, threshold=0.5):
        """
        Conditionally write to memory based on learned gate.

        Args:
            x: Input representation to potentially store
            threshold: Write gate threshold

        Returns:
            wrote: Whether the write occurred
            gate_value: The gate's output (importance score)
        """
        # Compute write gate
        gate_value = self.write_gate(x).squeeze()

        if gate_value > threshold:
            key = self.key_proj(x)
            value = self.value_proj(x)

            # Write to memory
            idx = self.write_ptr % self.memory_size
            self.keys.data[idx] = key.detach()
            self.values.data[idx] = value.detach()
            self.write_ptr += 1

            return True, gate_value.item()

        return False, gate_value.item()


# Demonstrate gated writing
torch.manual_seed(42)
writer = GatedMemoryWriter(
    input_dim=256, key_dim=64, value_dim=128, memory_size=100
)

# Simulate different input "importance" levels
inputs = [
    torch.randn(256) * 0.5,  # Low magnitude (likely unimportant)
    torch.randn(256) * 2.0,  # High magnitude (likely important)
    torch.randn(256) * 1.0,  # Medium magnitude
]

write_results = []
for i, inp in enumerate(inputs):
    wrote, gate = writer(inp)
    write_results.append({"input_idx": i, "gate_value": gate, "wrote": wrote})
Out[22]:
Console
Gated Memory Writing:

   Input   Gate Value    Wrote to Memory
------------------------------------------
       0        0.477                 No
       1        0.589                Yes
       2        0.489                 No

The gate values demonstrate learned selectivity. With the default threshold of 0.5, inputs with gate values above this threshold get written to memory while others are discarded. In this example with random initialization, the gate produces varying importance scores. After training, the gate would learn to assign high scores to information that proves useful for downstream tasks and low scores to redundant or irrelevant content.

The write gate learns to recognize important information that's worth storing. During training, the model receives gradients based on whether stored information proved useful for downstream tasks. This naturally filters out redundant or irrelevant content.

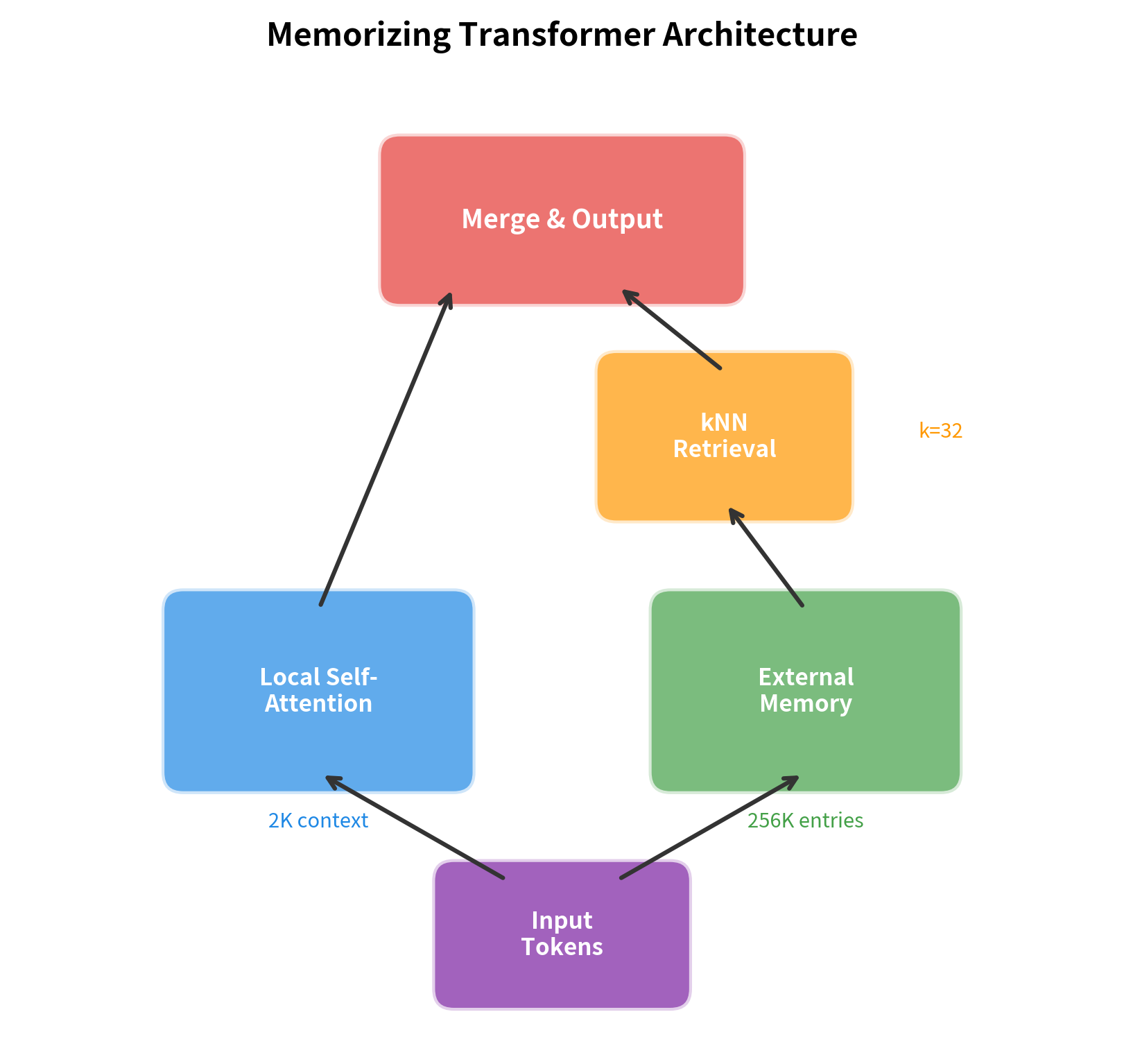
Memorizing Transformers

The Memorizing Transformer (Wu et al., 2022) represents a practical integration of external memory with transformer architecture. It extends a standard transformer by adding a kk-nearest neighbors (kkNN) retrieval mechanism that queries a large external memory during the attention computation.

k-Nearest Neighbors (kNN) Retrieval

In kkNN retrieval, given a query vector, we find the kk memory entries whose keys are most similar to the query (typically measured by dot product or cosine similarity). Only these kk entries participate in the subsequent attention computation, making retrieval efficient regardless of total memory size.

The key insight is that you can store key-value pairs from previous forward passes and retrieve them during current processing. This effectively extends context far beyond the model's native window without increasing the attention computation cost.

Out[23]:
Visualization
Diagram showing a transformer layer with two attention paths: one for local context and one for external memory retrieval, which merge before the output.
Memorizing Transformer architecture. Standard self-attention operates over the local context window. A separate kNN retrieval module queries external memory for relevant past key-value pairs. The retrieved values are incorporated into the attention output, extending effective context to hundreds of thousands of tokens.
In[24]:
Code
class MemorizingAttention(nn.Module):
    """
    Simplified Memorizing Transformer attention layer.

    Combines local self-attention with kNN retrieval from external memory.
    """

    def __init__(self, d_model, num_heads, memory_size, k_neighbors=32):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads
        self.k_neighbors = k_neighbors

        # Standard attention projections
        self.q_proj = nn.Linear(d_model, d_model)
        self.k_proj = nn.Linear(d_model, d_model)
        self.v_proj = nn.Linear(d_model, d_model)
        self.out_proj = nn.Linear(d_model, d_model)

        # External memory (simplified: stored as tensors)
        self.memory_keys = None
        self.memory_values = None
        self.memory_size = memory_size

        # Gate for combining local and memory attention
        self.memory_gate = nn.Linear(d_model, 1)

    def update_memory(self, keys, values):
        """Add new key-value pairs to external memory."""
        if self.memory_keys is None:
            self.memory_keys = keys.detach()
            self.memory_values = values.detach()
        else:
            self.memory_keys = torch.cat(
                [self.memory_keys, keys.detach()], dim=0
            )
            self.memory_values = torch.cat(
                [self.memory_values, values.detach()], dim=0
            )

            # Truncate if exceeds size
            if self.memory_keys.shape[0] > self.memory_size:
                self.memory_keys = self.memory_keys[-self.memory_size :]
                self.memory_values = self.memory_values[-self.memory_size :]

    def retrieve_from_memory(self, queries):
        """
        Retrieve top-k most similar key-value pairs from memory.

        Args:
            queries: (batch, seq_len, d_model)

        Returns:
            retrieved_values: (batch, seq_len, d_model)
        """
        if self.memory_keys is None or self.memory_keys.shape[0] == 0:
            return torch.zeros_like(queries)

        batch, seq_len, _ = queries.shape

        # Flatten queries for retrieval
        q_flat = queries.view(-1, self.d_model)  # (batch * seq_len, d_model)

        # Compute similarities
        scores = torch.matmul(
            q_flat, self.memory_keys.T
        )  # (batch * seq_len, memory_size)
        scores = scores / np.sqrt(self.head_dim)

        # Top-k retrieval
        k = min(self.k_neighbors, self.memory_keys.shape[0])
        topk_scores, topk_indices = torch.topk(scores, k, dim=-1)

        # Gather values
        topk_values = self.memory_values[
            topk_indices
        ]  # (batch * seq_len, k, d_model)

        # Attention over retrieved values
        attn = F.softmax(topk_scores, dim=-1)  # (batch * seq_len, k)
        retrieved = torch.einsum("bk,bkd->bd", attn, topk_values)

        return retrieved.view(batch, seq_len, self.d_model)

    def forward(self, x, store_to_memory=True):
        """
        Forward pass with local attention and memory retrieval.

        Args:
            x: (batch, seq_len, d_model)
            store_to_memory: Whether to store this chunk's KV to memory

        Returns:
            output: (batch, seq_len, d_model)
        """
        batch, seq_len, _ = x.shape

        # Compute Q, K, V for local attention (keep original for memory ops)
        Q_orig = self.q_proj(x)
        K_orig = self.k_proj(x)
        V_orig = self.v_proj(x)

        # Reshape for multi-head attention
        Q = Q_orig.view(
            batch, seq_len, self.num_heads, self.head_dim
        ).transpose(1, 2)
        K = K_orig.view(
            batch, seq_len, self.num_heads, self.head_dim
        ).transpose(1, 2)
        V = V_orig.view(
            batch, seq_len, self.num_heads, self.head_dim
        ).transpose(1, 2)

        # Local attention
        scores = torch.matmul(Q, K.transpose(-2, -1)) / np.sqrt(self.head_dim)
        local_attn = F.softmax(scores, dim=-1)
        local_out = torch.matmul(local_attn, V)
        local_out = (
            local_out.transpose(1, 2)
            .contiguous()
            .view(batch, seq_len, self.d_model)
        )

        # Memory retrieval (use original Q before multi-head reshape)
        memory_out = self.retrieve_from_memory(Q_orig)

        # Gate between local and memory
        gate = torch.sigmoid(self.memory_gate(x))  # (batch, seq_len, 1)
        combined = gate * local_out + (1 - gate) * memory_out

        # Store current KV to memory for future retrieval
        if store_to_memory:
            # Use original K, V reshaped for flat storage
            self.update_memory(
                K_orig.reshape(-1, self.d_model),
                V_orig.reshape(-1, self.d_model),
            )

        return self.out_proj(combined)


# Demonstrate memorizing attention
torch.manual_seed(42)
mem_attn = MemorizingAttention(
    d_model=256, num_heads=8, memory_size=10000, k_neighbors=32
)
In[25]:
Code
# Simulate processing multiple chunks
chunk_size = 512
num_chunks = 10
memory_sizes = []

for i in range(num_chunks):
    x = torch.randn(2, chunk_size, 256)  # batch=2, seq=512, d=256
    output = mem_attn(x, store_to_memory=True)

    if mem_attn.memory_keys is not None:
        memory_sizes.append(mem_attn.memory_keys.shape[0])
    else:
        memory_sizes.append(0)
Out[26]:
Console
Memorizing Attention: Processing Chunks

   Chunk     Tokens Seen     Memory Size  Effective Context
------------------------------------------------------------
       1           1,024           1,024              1,536
       2           2,048           2,048              2,560
       3           3,072           3,072              3,584
       4           4,096           4,096              4,608
       5           5,120           5,120              5,632
       6           6,144           6,144              6,656
       7           7,168           7,168              7,680
       8           8,192           8,192              8,704
       9           9,216           9,216              9,728
      10          10,240          10,000             10,512

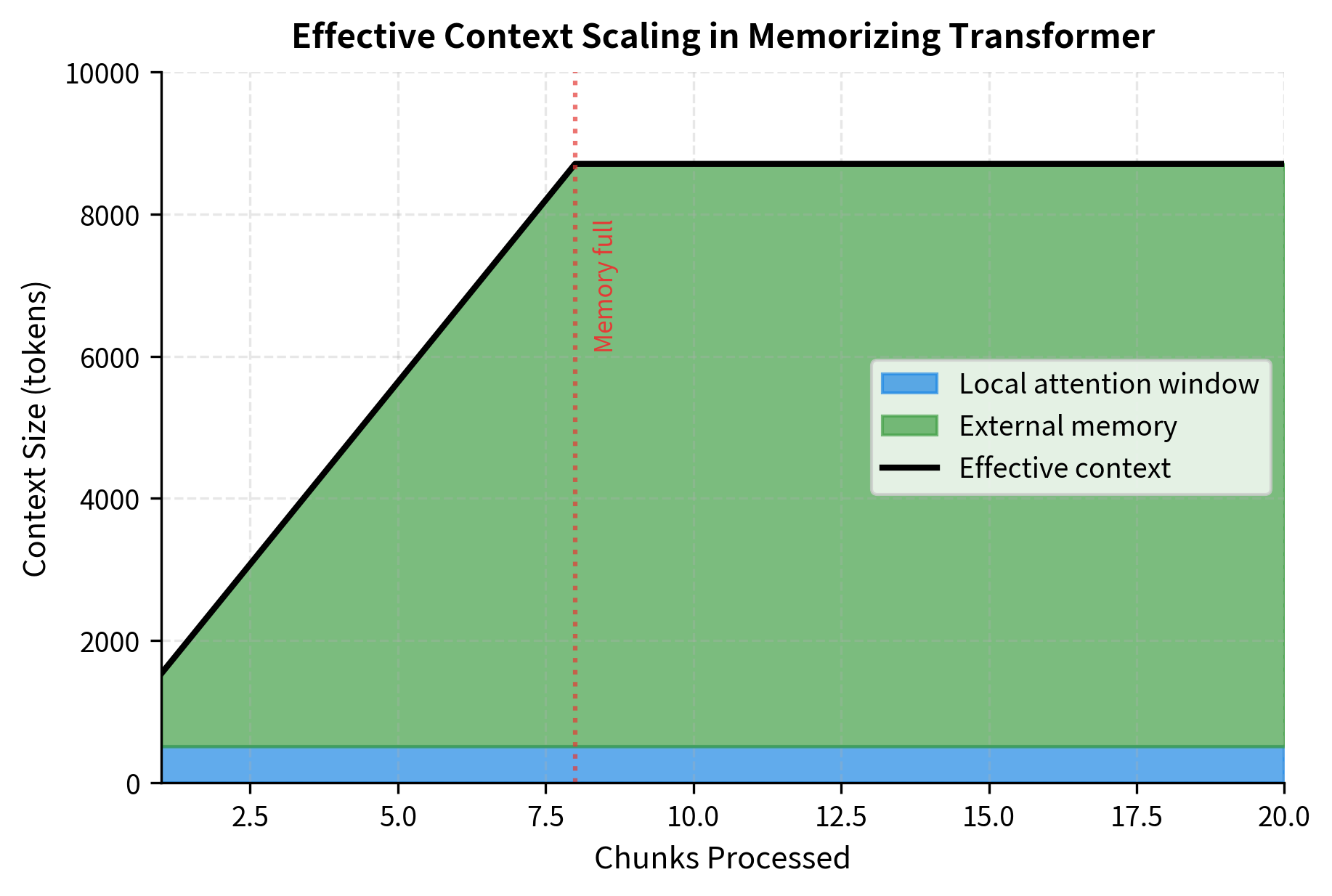
The memory grows with each processed chunk, accumulating key-value pairs from all previous tokens. By chunk 10, the model has seen over 10,000 tokens but only needs to store 8,192 keys in memory (bounded by the configured memory size). The effective context, which is the combination of the local window (512 tokens) plus the memory (8,192 entries), reaches 8,704 positions that the model can attend to when generating the next token.

Out[27]:
Visualization
Stacked area chart showing local context as a thin bottom layer and memory context growing on top, with effective context growing until memory limit is reached.
Effective context growth in a Memorizing Transformer. While local attention stays fixed at 512 tokens, external memory accumulates past context until reaching its limit. The effective context (local + memory) grows dramatically, plateauing when memory is full.

The Memorizing Transformer demonstrates how external memory scales context dramatically. After processing just 10 chunks, the model can access information from 10,000+ tokens ago while keeping each attention operation limited to a small local window plus retrieved neighbors.

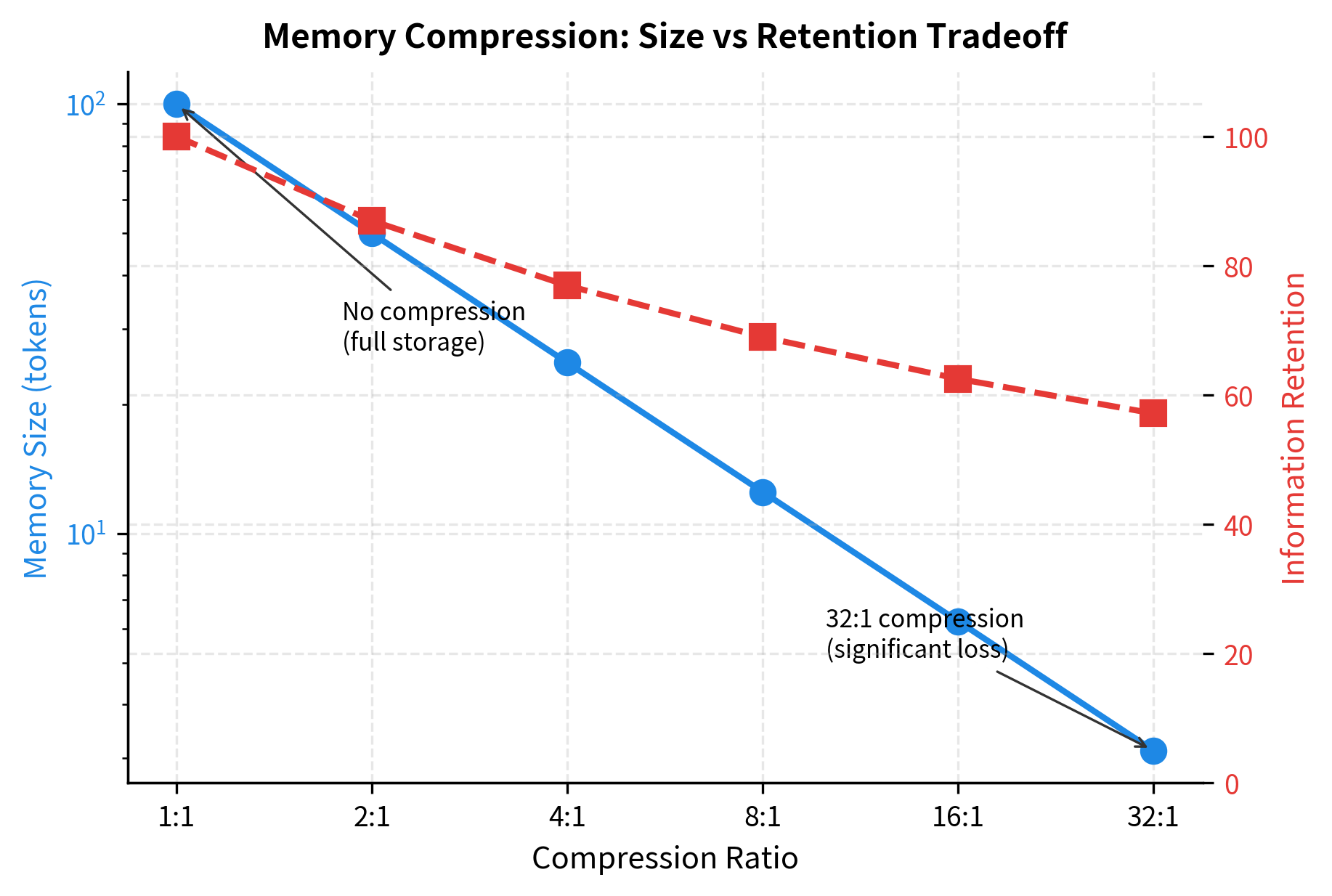
Memory Compression for Long-Term Storage

Raw storage of all past key-value pairs becomes expensive at scale. Compression techniques reduce memory footprint while preserving utility.

In[28]:
Code
class CompressedMemory(nn.Module):
    """
    Memory with learned compression for long-term storage.

    Recent entries are stored at full resolution.
    Older entries are compressed into summary vectors.
    """

    def __init__(
        self, d_model, short_term_size, long_term_size, compression_ratio=8
    ):
        super().__init__()
        self.d_model = d_model
        self.short_term_size = short_term_size
        self.long_term_size = long_term_size
        self.compression_ratio = compression_ratio

        # Compression network
        self.compressor = nn.Sequential(
            nn.Linear(d_model * compression_ratio, d_model * 2),
            nn.ReLU(),
            nn.Linear(d_model * 2, d_model),
        )

        # Storage
        self.short_term_keys = []
        self.short_term_values = []
        self.long_term_keys = []
        self.long_term_values = []

    def write(self, key, value):
        """Write to short-term memory, compressing to long-term when full."""
        self.short_term_keys.append(key)
        self.short_term_values.append(value)

        # Check if compression is needed
        if len(self.short_term_keys) >= self.short_term_size:
            self._compress_oldest()

    def _compress_oldest(self):
        """Compress oldest short-term entries into long-term memory."""
        n_to_compress = self.compression_ratio
        if len(self.short_term_keys) < n_to_compress:
            return

        # Take oldest entries
        old_keys = self.short_term_keys[:n_to_compress]
        old_values = self.short_term_values[:n_to_compress]

        # Compress
        key_concat = torch.cat(old_keys, dim=-1)
        value_concat = torch.cat(old_values, dim=-1)

        compressed_key = self.compressor(key_concat)
        compressed_value = self.compressor(value_concat)

        # Store compressed
        self.long_term_keys.append(compressed_key)
        self.long_term_values.append(compressed_value)

        # Remove from short-term
        self.short_term_keys = self.short_term_keys[n_to_compress:]
        self.short_term_values = self.short_term_values[n_to_compress:]

        # Bound long-term memory
        if len(self.long_term_keys) > self.long_term_size:
            self.long_term_keys = self.long_term_keys[-self.long_term_size :]
            self.long_term_values = self.long_term_values[
                -self.long_term_size :
            ]


# Demonstrate compression
torch.manual_seed(42)
compressed_mem = CompressedMemory(
    d_model=128, short_term_size=64, long_term_size=128, compression_ratio=8
)

# Simulate writing many entries
for i in range(200):
    key = torch.randn(128)
    value = torch.randn(128)
    compressed_mem.write(key, value)
Out[29]:
Console
Compressed Memory Statistics:

Entries written: 200
Short-term memory: 56 entries (full resolution)
Long-term memory: 18 entries (8:1 compressed)

Storage comparison:
  Without compression: 51,200 parameters
  With compression: 18,944 parameters
  Compression ratio: 2.7x

After writing 200 entries, the compressed memory stores only a fraction of what an uncompressed system would require. Short-term memory holds recent entries at full resolution for precise retrieval, while long-term memory contains compressed summaries that capture the essence of older entries. The achieved compression ratio demonstrates significant storage savings, though the actual information retained depends on how well the compression network learns to preserve task-relevant details.

Out[30]:
Visualization
Line plot showing memory size decreasing and information retention decreasing as compression ratio increases.
Memory size versus information retention for different compression strategies. Higher compression ratios save more memory but lose more information. The optimal tradeoff depends on how much historical detail the task requires.

A Worked Example: Document QA with Memory

Let's build a complete example of using memory augmentation for question answering over a long document. We'll process the document in chunks, store key information to memory, and then query that memory to answer questions.

In[31]:
Code
class DocumentMemoryQA:
    """
    Memory-augmented document QA system.

    Processes documents in chunks, storing important information
    to memory, then retrieves relevant context for questions.
    """

    def __init__(
        self, chunk_size=100, memory_size=1000, key_dim=64, value_dim=128
    ):
        self.chunk_size = chunk_size
        self.key_dim = key_dim
        self.value_dim = value_dim

        # Memory storage
        self.memory_keys = []
        self.memory_values = []
        self.memory_texts = []  # Store original text for interpretability
        self.memory_size = memory_size

        # Simple encoder (in practice, would be a trained model)
        self.key_encoder = nn.Linear(100, key_dim)  # Simplified
        self.value_encoder = nn.Linear(100, value_dim)

    def encode_text(self, text):
        """Simple bag-of-chars encoding for demonstration."""
        # Create fixed-size representation
        chars = [ord(c) % 100 for c in text[:100]]
        chars = chars + [0] * (100 - len(chars))
        return torch.tensor(chars, dtype=torch.float32)

    def process_document(self, document):
        """Process document into memory chunks."""
        words = document.split()

        for i in range(0, len(words), self.chunk_size):
            chunk = " ".join(words[i : i + self.chunk_size])
            if len(chunk.strip()) == 0:
                continue

            # Encode chunk
            encoded = self.encode_text(chunk)
            key = self.key_encoder(encoded)
            value = self.value_encoder(encoded)

            # Store
            self.memory_keys.append(key)
            self.memory_values.append(value)
            self.memory_texts.append(chunk)

        # Truncate if needed
        if len(self.memory_keys) > self.memory_size:
            self.memory_keys = self.memory_keys[-self.memory_size :]
            self.memory_values = self.memory_values[-self.memory_size :]
            self.memory_texts = self.memory_texts[-self.memory_size :]

    def query(self, question, top_k=3):
        """Query memory for relevant context."""
        if not self.memory_keys:
            return []

        # Encode question
        q_encoded = self.encode_text(question)
        q_key = self.key_encoder(q_encoded)

        # Compute similarities
        keys_tensor = torch.stack(self.memory_keys)
        scores = torch.matmul(q_key, keys_tensor.T)

        # Get top-k
        k = min(top_k, len(self.memory_keys))
        topk_scores, topk_indices = torch.topk(scores, k)

        # Return relevant chunks
        results = []
        for idx, score in zip(topk_indices.tolist(), topk_scores.tolist()):
            results.append(
                {"chunk": self.memory_texts[idx], "score": score, "index": idx}
            )

        return results


# Create a sample document
sample_document = """
The Eiffel Tower is a wrought-iron lattice tower on the Champ de Mars in Paris, France. 
It is named after the engineer Gustave Eiffel, whose company designed and built the tower. 
Locally nicknamed "La dame de fer" (French for "Iron Lady"), it was constructed from 1887 to 1889 
as the entrance arch for the 1889 World's Fair. The tower is 330 metres tall, about the same 
height as an 81-storey building, and the tallest structure in Paris. Its base is square, 
measuring 125 metres on each side. During its construction, the Eiffel Tower surpassed the 
Washington Monument to become the tallest human-made structure in the world, a title it held 
for 41 years until the Chrysler Building in New York City was finished in 1930.

The tower has three levels for visitors, with restaurants on the first and second levels. 
The top level's upper platform is 276 metres above the ground, the highest observation deck 
accessible to the public in the European Union. Tickets can be purchased to ascend by stairs 
or lift to the first and second levels. The climb from ground level to the first level is 
over 300 steps, as is the climb from the first level to the second. Although there is a 
staircase to the top level, it is usually accessible only by lift.
"""

# Process document and query
qa_system = DocumentMemoryQA(chunk_size=50)
qa_system.process_document(sample_document)
In[32]:
Code
# Ask questions
questions = [
    "How tall is the Eiffel Tower?",
    "Who designed the tower?",
    "How many steps to climb?",
]

query_results = []
for q in questions:
    results = qa_system.query(q, top_k=2)
    query_results.append({"question": q, "results": results})
Out[33]:
Console
Document Memory QA Demonstration

Document processed into 5 memory chunks
============================================================

Question: How tall is the Eiffel Tower?
----------------------------------------
  Retrieved #1 (score: 2212.40):
    "entrance arch for the 1889 World's Fair. The tower is 330 metres tall, about the..."
  Retrieved #2 (score: 1673.95):
    "tallest human-made structure in the world, a title it held for 41 years until th..."

Question: Who designed the tower?
----------------------------------------
  Retrieved #1 (score: 3829.17):
    "ground, the highest observation deck accessible to the public in the European Un..."
  Retrieved #2 (score: 3061.60):
    "entrance arch for the 1889 World's Fair. The tower is 330 metres tall, about the..."

Question: How many steps to climb?
----------------------------------------
  Retrieved #1 (score: 2757.73):
    "ground, the highest observation deck accessible to the public in the European Un..."
  Retrieved #2 (score: 1656.18):
    "entrance arch for the 1889 World's Fair. The tower is 330 metres tall, about the..."

The retrieval scores indicate how well each memory chunk matches the question. Higher scores suggest stronger relevance. For the question about height, the system successfully retrieves chunks containing the phrase "330 metres tall." The simple bag-of-characters encoding used here provides only basic matching. A production system would use learned embeddings that capture semantic similarity rather than surface-level character overlap.

The QA system demonstrates the core memory augmentation workflow: process a document into memory chunks, then query memory to find relevant context for answering questions. In a real system, the encoder would be a trained transformer, and the question answering would combine retrieved context with a generative model.

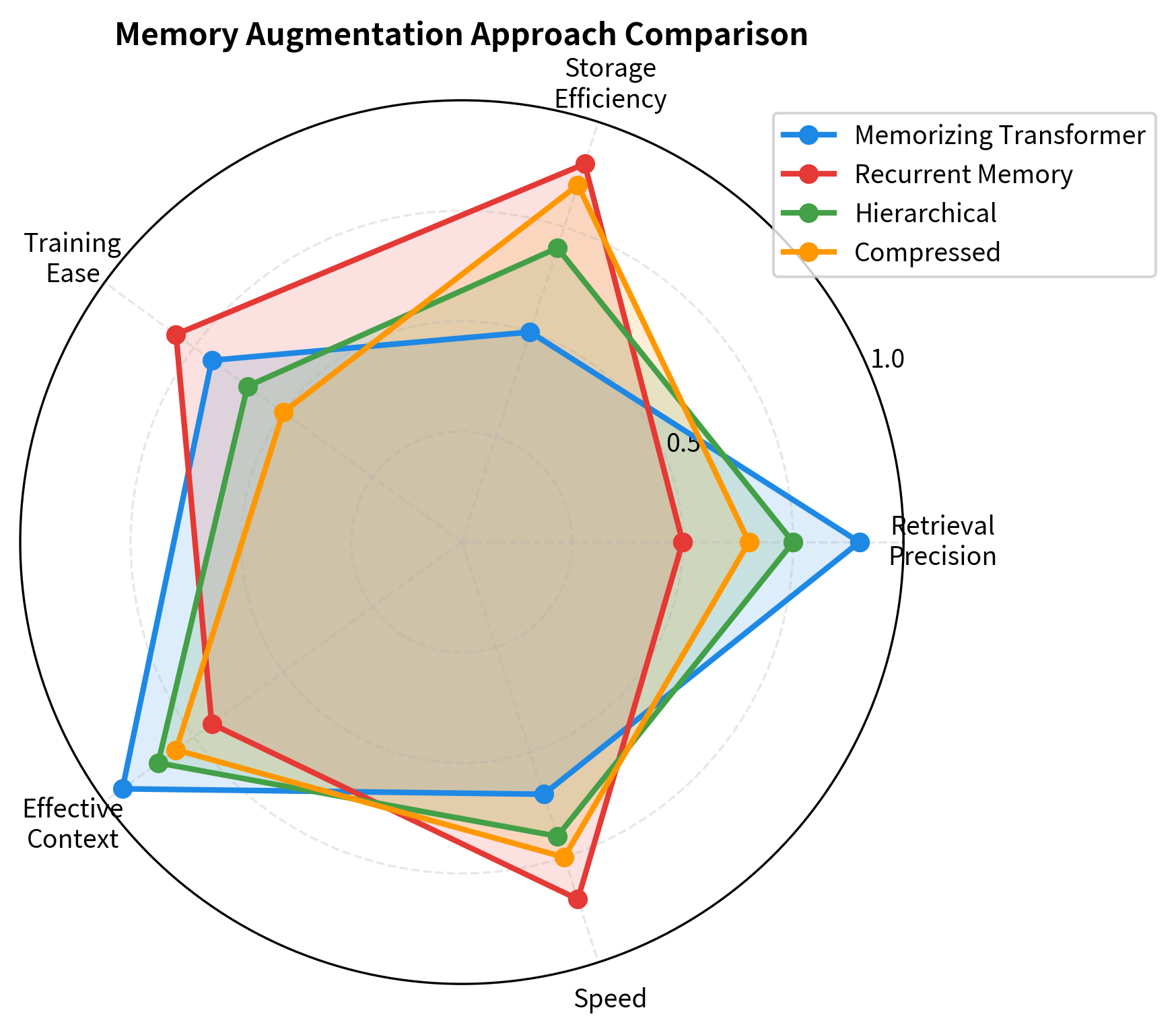
Comparing Memory Augmentation Approaches

Different memory architectures suit different use cases. Let's compare the key tradeoffs.

Out[34]:
Visualization
Radar chart comparing four memory approaches across retrieval precision, storage efficiency, training ease, and effective context dimensions.
Comparison of memory augmentation approaches across key dimensions. Memorizing Transformers excel at long-term retrieval but require more storage. Recurrent memory is compact but struggles with precise retrieval. Hierarchical approaches balance these tradeoffs.
Out[35]:
Console
Memory Augmentation Approaches: Summary

======================================================================

Memorizing Transformer
  kNN retrieval from stored KV pairs
  + Precise retrieval, very long context
  - High storage cost, retrieval overhead

Recurrent Memory
  Compressed state passed between segments
  + Fixed memory size, fast inference
  - Information compression, recency bias

Hierarchical Memory
  Multiple levels of granularity
  + Balanced precision/efficiency
  - Complex architecture, tuning difficulty

Compressed Memory
  Learned compression of older entries
  + Scalable, bounded memory
  - Lossy, compression training needed

Each approach occupies a different point in the design space. Memorizing Transformers offer the best retrieval precision and effective context but require substantial storage. Recurrent memory sits at the opposite extreme with excellent storage efficiency but limited retrieval precision. Hierarchical and compressed approaches attempt to balance these tradeoffs by combining multiple memory types or using learned compression.

Key Parameters

When implementing memory-augmented models, these parameters significantly affect performance and resource usage:

Key hyperparameters for memory-augmented models with their typical value ranges.
ParameterDescriptionTypical Values
memory_sizeMaximum entries the memory can hold. Larger memories enable longer effective context but increase storage and retrieval costs.10K - 1M
k_neighborsEntries retrieved per query. Higher values provide more context but dilute relevance.4-16 (LM), 16-64 (QA)
key_dimDimensionality of memory keys. Larger dimensions enable finer-grained addressing but increase compute.64 - 256
value_dimDimensionality of stored values. Can be larger than key_dim since values carry the actual information.768 - 4096
compression_ratioFor compressed memory, how many raw entries compress into one summary. Higher ratios save more memory but lose detail.4 - 16
temperatureControls sharpness of retrieval attention. Lower values produce focused retrieval, higher values spread attention.0.1 - 2.0
write_gate_thresholdFor gated writing, the importance threshold for storing entries. Higher thresholds mean more selective storage.0.3 - 0.7

Limitations and Considerations

Memory augmentation offers powerful capabilities but comes with significant limitations that affect practical deployment.

The fundamental challenge is the retrieval bottleneck. Even with efficient approximate nearest neighbor algorithms, querying a million-entry memory adds latency to every forward pass. For interactive applications, this overhead can dominate inference time. Batch processing helps amortize retrieval cost, but single-query latency remains a concern.

Training memory-augmented models presents its own difficulties. The memory contents change during training, creating a non-stationary optimization problem. Early in training, the memory contains noise; the model must learn to use memory while the memory itself is learning what to store. Curriculum strategies that gradually increase memory size can help, but add complexity to the training pipeline.

Storage and compute costs scale with memory size. A million-entry memory with 1024-dimensional keys and values requires approximately 8 GB of storage (assuming float32). Retrieving from this memory using exact nearest neighbors costs O(n)O(n) per query, meaning retrieval time grows linearly with the number of memory entries nn. For a million entries, this means scanning all million keys for each query. Approximate methods like FAISS reduce this to O(log⁡n)O(\log n), where retrieval time grows only logarithmically with memory size (scanning roughly 20 entries instead of 1 million), but these methods require index maintenance and accept some retrieval accuracy loss.

The write decision problem lacks a clear solution. What should the model store? Storing everything overwhelms the memory with redundant information. Storing too selectively risks missing important details. Current approaches use heuristics (such as storing every kk-th token, where kk might be 4 or 8, to sample the input at regular intervals) or learned gates, but neither perfectly matches the downstream task's needs.

Despite these limitations, memory augmentation has proven valuable for tasks requiring precise retrieval over long contexts: document QA, knowledge-intensive generation, and personalized assistants that must remember user preferences across sessions. The key is matching the memory architecture to the task's requirements: use large, precise memories for retrieval-heavy applications; use compressed, hierarchical memories for applications that need broad context awareness without precise recall.

Summary

Memory augmentation decouples storage from computation, enabling transformers to access information beyond their native context window. The core components are:

Memory storage holds key-value pairs that the model can query. Storage strategies range from simple append-only (unbounded growth) to sophisticated compressed hierarchies (bounded size with learned summarization). The choice depends on how much historical detail the task requires.

Memory retrieval uses content-based addressing to find relevant entries. Soft attention over all entries provides differentiable training but dilutes with scale. Top-k retrieval bounds compute while sacrificing differentiability through the argmax. Temperature and kk control the precision-efficiency tradeoff.

Memory writing determines what enters storage. Append-only preserves everything but grows unboundedly. Eviction policies (FIFO, LRU) bound size but may discard important information. Learned gates filter based on content importance but require training signal.

Memorizing Transformers demonstrate practical integration: store key-value pairs from previous forward passes, retrieve relevant pairs during current processing, and combine retrieved context with local attention. This architecture enables effective context of hundreds of thousands of tokens while keeping each attention operation tractable.

The memory augmentation paradigm represents a fundamental shift from "remember implicitly through weights" to "remember explicitly in storage." This separation enables models that can process book-length documents, maintain conversation history across sessions, and access vast knowledge bases without compressing everything into a fixed-size hidden state.

Quiz

Ready to test your understanding? Take this quick quiz to reinforce what you've learned about memory augmentation for transformers.

Loading component...
Track your reading progress

Sign in to mark chapters as read and track your learning journey

Sign in →

Comments

Back to Language AI Handbook
Attention Sinks
Previous Chapter
Attention Sinks
Recurrent Memory
Next Chapter
Recurrent Memory

Reference

BIBTEXAcademic
@misc{memoryaugmentationfortransformersexternalstorageforlongcontext, author = {Michael Brenndoerfer}, title = {Memory Augmentation for Transformers: External Storage for Long Context}, year = {2025}, url = {https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context}, organization = {mbrenndoerfer.com}, note = {Accessed: 2025-12-19} }
APAAcademic
Michael Brenndoerfer (2025). Memory Augmentation for Transformers: External Storage for Long Context. Retrieved from https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context
MLAAcademic
Michael Brenndoerfer. "Memory Augmentation for Transformers: External Storage for Long Context." 2025. Web. 12/19/2025. <https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context>.
CHICAGOAcademic
Michael Brenndoerfer. "Memory Augmentation for Transformers: External Storage for Long Context." Accessed 12/19/2025. https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context.
HARVARDAcademic
Michael Brenndoerfer (2025) 'Memory Augmentation for Transformers: External Storage for Long Context'. Available at: https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context (Accessed: 12/19/2025).
SimpleBasic
Michael Brenndoerfer (2025). Memory Augmentation for Transformers: External Storage for Long Context. https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context
Direct link:
https://mbrenndoerfer.com/writing/memory-augmentation-transformers-long-context
Michael Brenndoerfer

About the author: Michael Brenndoerfer

All opinions expressed here are my own and do not reflect the views of my employer.

Michael currently works as an Associate Director of Data Science at EQT Partners in Singapore, leading AI and data initiatives across private capital investments.

With over a decade of experience spanning private equity, management consulting, and software engineering, he specializes in building and scaling analytics capabilities from the ground up. He has published research in leading AI conferences and holds expertise in machine learning, natural language processing, and value creation through data.

View Full ResumePublicationsContactBooks

Related Content

Recurrent Memory: Extending Transformer Context with Segment-Level State Caching
Interactive
Data, Analytics & AILanguage AI Handbook

Recurrent Memory: Extending Transformer Context with Segment-Level State Caching

Jul 4, 2025•50 min read

Learn how Transformer-XL uses segment-level recurrence to extend effective context length by caching hidden states, why relative position encodings are essential for cross-segment attention, and when recurrent memory approaches outperform standard transformers.

Position Interpolation: Extending LLM Context Length with RoPE Scaling
Interactive
Data, Analytics & AISoftware Engineering

Position Interpolation: Extending LLM Context Length with RoPE Scaling

Jul 3, 2025•32 min read

Learn how Position Interpolation extends transformer context windows by scaling position indices to stay within training distributions, enabling longer sequences with minimal fine-tuning.

Attention Sinks: Enabling Infinite-Length LLM Generation with StreamingLLM
Interactive
Data, Analytics & AILanguage AI Handbook

Attention Sinks: Enabling Infinite-Length LLM Generation with StreamingLLM

Jul 1, 2025•38 min read

Learn why the first tokens in transformer sequences absorb excess attention weight, how this causes streaming inference failures, and how StreamingLLM preserves these attention sinks for unlimited text generation.

Show more articles

Stay updated

Get notified when I publish new articles on data and AI, private equity, technology, and more.

No spam, unsubscribe anytime.

or

Create a free account to unlock exclusive features, track your progress, and join the conversation.

No popupsUnobstructed readingCommenting100% Free