Learn how top-k sampling truncates vocabulary to the k most probable tokens, eliminating incoherent outputs while preserving diversity in language model generation.

This article is part of the free-to-read Language AI Handbook
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Top-k Sampling
When a language model generates text, it produces a probability distribution over tens of thousands of possible next tokens. Greedy decoding picks the single most likely token at each step, which leads to repetitive and predictable output. Temperature scaling makes the distribution more uniform, but it raises the probability of every token, including nonsensical ones. Top-k sampling offers a different solution: keep only the most probable tokens and sample from this truncated distribution.
The core idea is straightforward. Rather than considering all 50,000+ tokens in the vocabulary, top-k sampling zeros out the probability of everything outside the top candidates. This eliminates the long tail of unlikely tokens while preserving meaningful diversity among the plausible choices. The result is text that reads naturally without veering into incoherence.
This chapter explores top-k sampling in detail. We'll examine the mathematics behind truncation, implement the algorithm from scratch, discuss how to select appropriate values of , and combine top-k with temperature for fine-grained control over generation quality.
The Problem with Full Vocabulary Sampling
Before diving into top-k, let's understand why sampling from the full vocabulary distribution causes problems. A trained language model assigns non-zero probability to every token, even ones that make no sense in context.
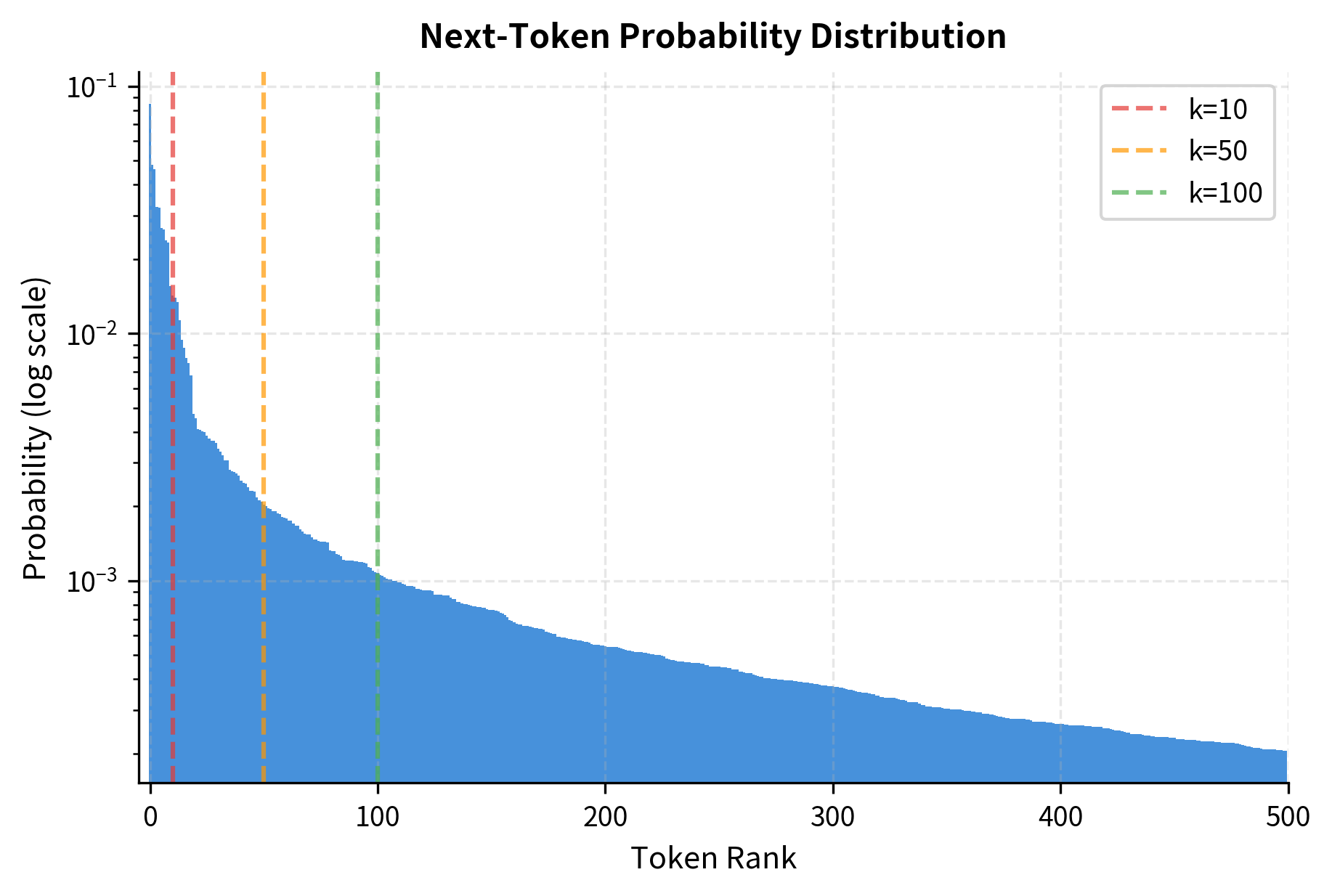
Most of the vocabulary mass sits in the long tail of tokens with tiny probabilities. While each token individually has near-zero chance of selection, collectively they can represent a substantial fraction of the total probability. Sampling from this full distribution occasionally produces bizarre tokens that derail generation.
The figure illustrates why the long tail is problematic. After the first few tokens, probability drops rapidly, but thousands of tokens retain some small probability. Summed together, this tail can be significant. If we sample proportionally, low-probability tokens occasionally win, producing outputs like "The capital of France is ????????" or "The capital of France is asdf".
How Top-k Sampling Works
Now that we understand the problem, let's build up the solution piece by piece. The core insight behind top-k sampling is simple: if most of the probability mass concentrates in a handful of tokens, why not just sample from those and ignore the rest?
The Intuition: Focus on What Matters
Think about how you complete sentences. Given "The capital of France is", you don't mentally consider every possible word in English. You immediately focus on a small set of plausible continuations: "Paris", maybe "a", "the", or "known". Your mental probability distribution isn't uniform across all words, and neither is the model's. Top-k sampling formalizes this intuition by explicitly restricting attention to the most likely candidates.
The approach works in five steps:
- Compute probabilities: The model outputs a distribution over all vocabulary tokens
- Rank by likelihood: Sort tokens from most to least probable
- Keep the top k: Select only the highest-probability tokens
- Zero out the rest: Set all other token probabilities to exactly zero
- Renormalize and sample: Rescale the remaining probabilities so they sum to 1, then sample
Top-k sampling restricts the sampling space to the most probable tokens. After zeroing out tokens outside the top-, the remaining probabilities are renormalized before sampling.
From Intuition to Mathematics
Let's formalize this process. At generation step , the model has seen context (all previous tokens) and outputs a probability for each possible next token . This distribution spans the entire vocabulary, but we only want to sample from the top performers.
First, we need to identify which tokens make the cut. Define as the set containing the tokens with highest probability. If the vocabulary has 50,000 tokens and , then contains exactly the 50 most likely tokens for this specific context.
Now we need to handle a subtle issue: after removing tokens from consideration, the probabilities of the remaining tokens no longer sum to 1. A probability distribution must sum to 1 for sampling to work correctly. The solution is renormalization. We divide each remaining probability by the sum of all kept probabilities.
This gives us the formal definition of top-k sampling:
where:
- : a candidate token at position
- : the context (all tokens before position )
- : the original probability the model assigns to token given the context
- : the set of tokens with highest probability under
- : the normalization constant, which equals the sum of probabilities of the top- tokens
- : the renormalized probability used for sampling
Why Renormalization Preserves Relative Probabilities
A critical property of this construction is that renormalization preserves the relative likelihood of tokens within the top-. Consider two tokens, "Paris" with original probability 0.30 and "the" with probability 0.15. In the original distribution, "Paris" is exactly twice as likely as "the".
After truncation, suppose the top- tokens have cumulative probability . The renormalized probabilities become:
- "Paris":
- "the":
Notice that . The ratio is preserved! This happens because we divide both probabilities by the same constant . Renormalization scales all probabilities equally, maintaining their relative ordering and ratios.
This property matters because it means top-k sampling respects the model's preferences among plausible tokens. We're not arbitrarily reweighting tokens; we're simply restricting which tokens can be sampled while honoring the model's ranking within that restricted set.
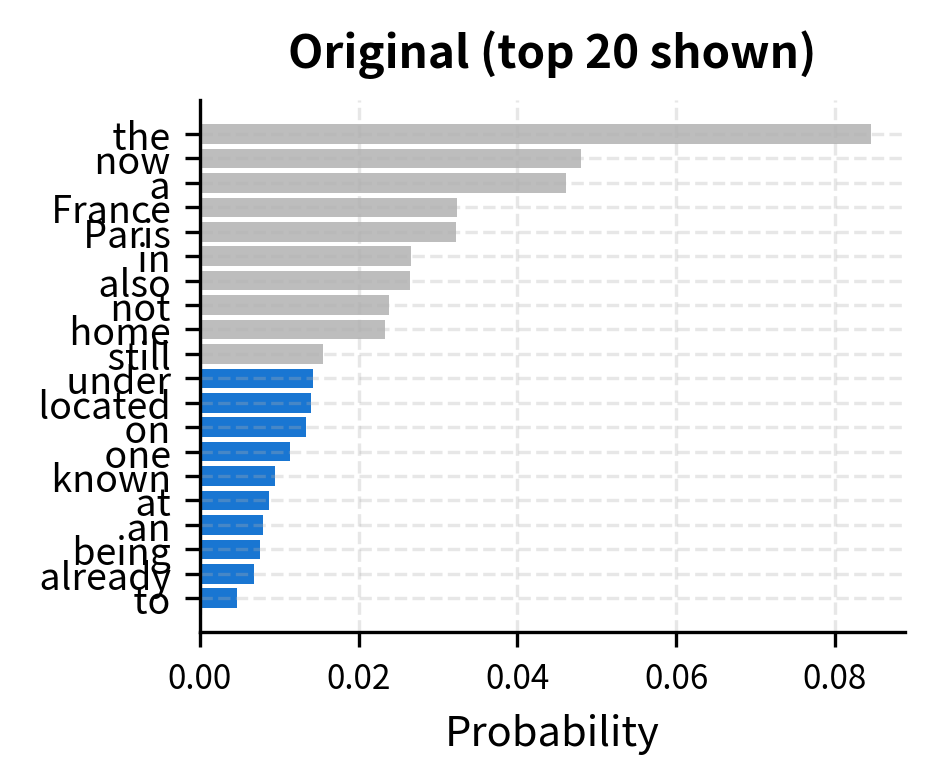
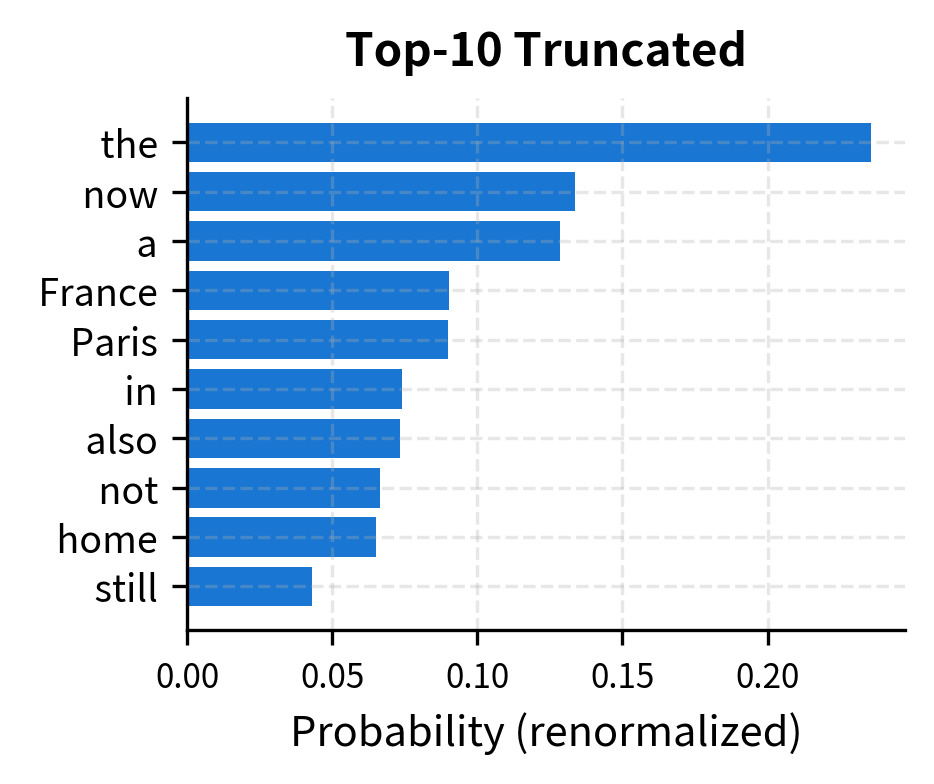
Visualizing the Truncation
The following visualization shows this process concretely. On the left, we see the original distribution over the top 20 tokens. On the right, we see the truncated distribution after keeping only tokens and renormalizing.
Implementing Top-k Sampling
With the mathematics established, let's translate the algorithm into code. The implementation is straightforward, but walking through it step by step reveals how each line corresponds to a piece of the formula.
Building the Core Sampler
Our implementation needs to accomplish four things:
- Apply temperature scaling to the logits
- Find the highest-scoring tokens
- Convert those scores to a valid probability distribution
- Sample one token from that distribution
The key insight is that we don't need to explicitly zero out the non-top-k tokens. Instead, we can compute softmax over only the top-k logits, which automatically gives us a properly normalized distribution over just those tokens.
Let's trace through each step:
- Temperature scaling divides each logit by the temperature, controlling how peaked or flat the distribution becomes
torch.topkefficiently finds the largest values and their positions in the vocabulary, returning both the values and their indices- Softmax over top-k values computes using only the kept tokens, which is equivalent to the renormalization step in our formula
torch.multinomialsamples according to the probability distribution, returning an index into our top-k list- Index mapping converts the sampled position (0 to k-1) back to the actual vocabulary token ID
Seeing It in Action
Let's sample multiple times from the same context to see the variety top-k produces:
Notice how all samples are reasonable completions. With , we're sampling from only the five most likely tokens, which for this factual prompt are all sensible choices. The variation comes from the probabilistic sampling, but every option is plausible.
From Single Tokens to Full Text Generation
A single sample is interesting, but the real power of top-k sampling emerges when we generate entire sequences. Each token we generate becomes part of the context for the next token, creating a chain of sampling decisions.
The generation loop follows a simple pattern: get logits, sample a token, append it to the sequence, repeat. At each step, top-k ensures we only consider reasonable continuations.
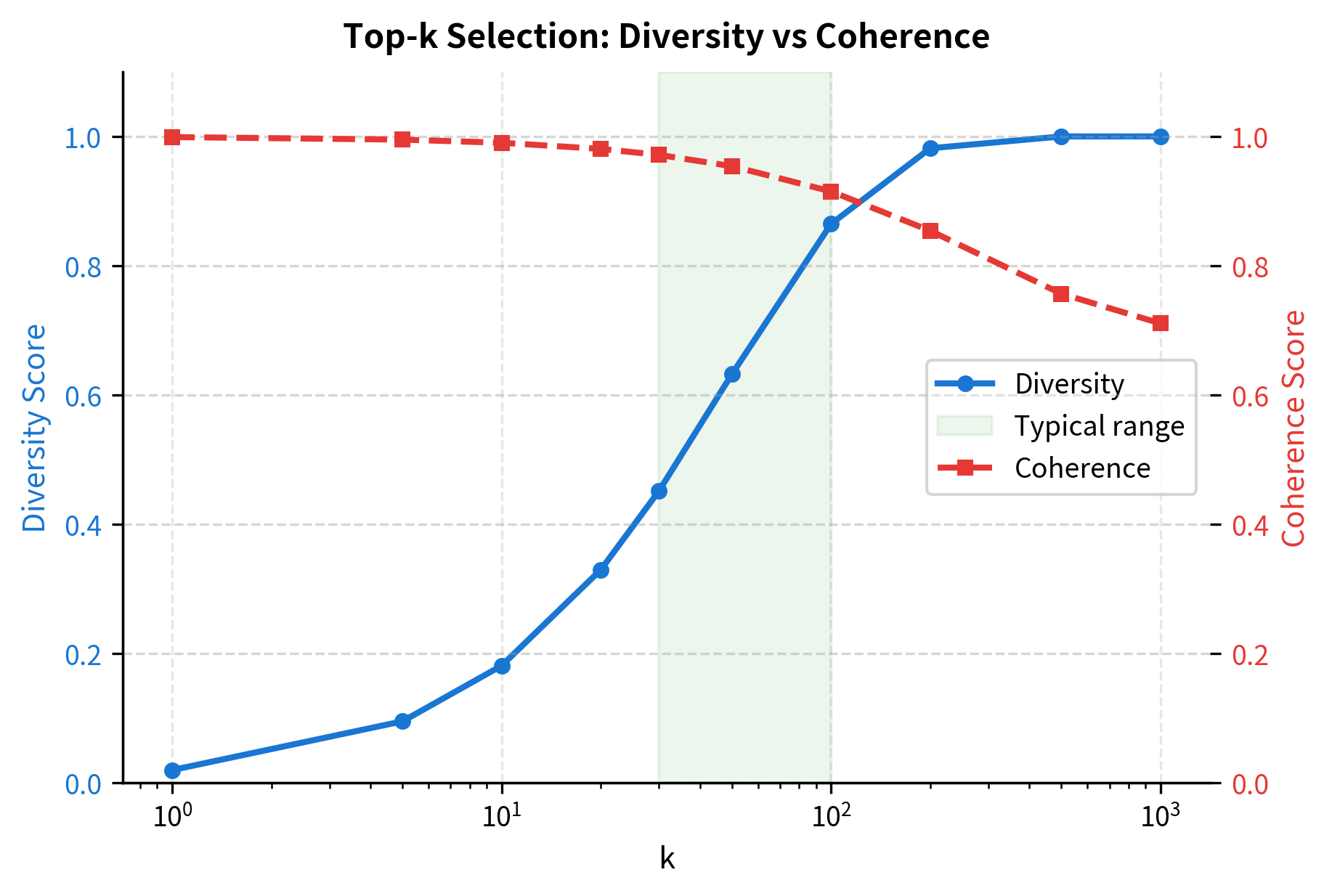
The Effect of Different k Values
Now we can see how shapes the character of generated text. Smaller means stricter filtering, keeping only the most confident predictions. Larger allows more exploration of the probability space.
The outputs reveal distinct personalities. With , the text tends toward common, expected phrasings. With , there's more room for varied word choices while maintaining fluency. With , the model has significant freedom, though even here, we've eliminated the vast majority of the vocabulary's long tail.
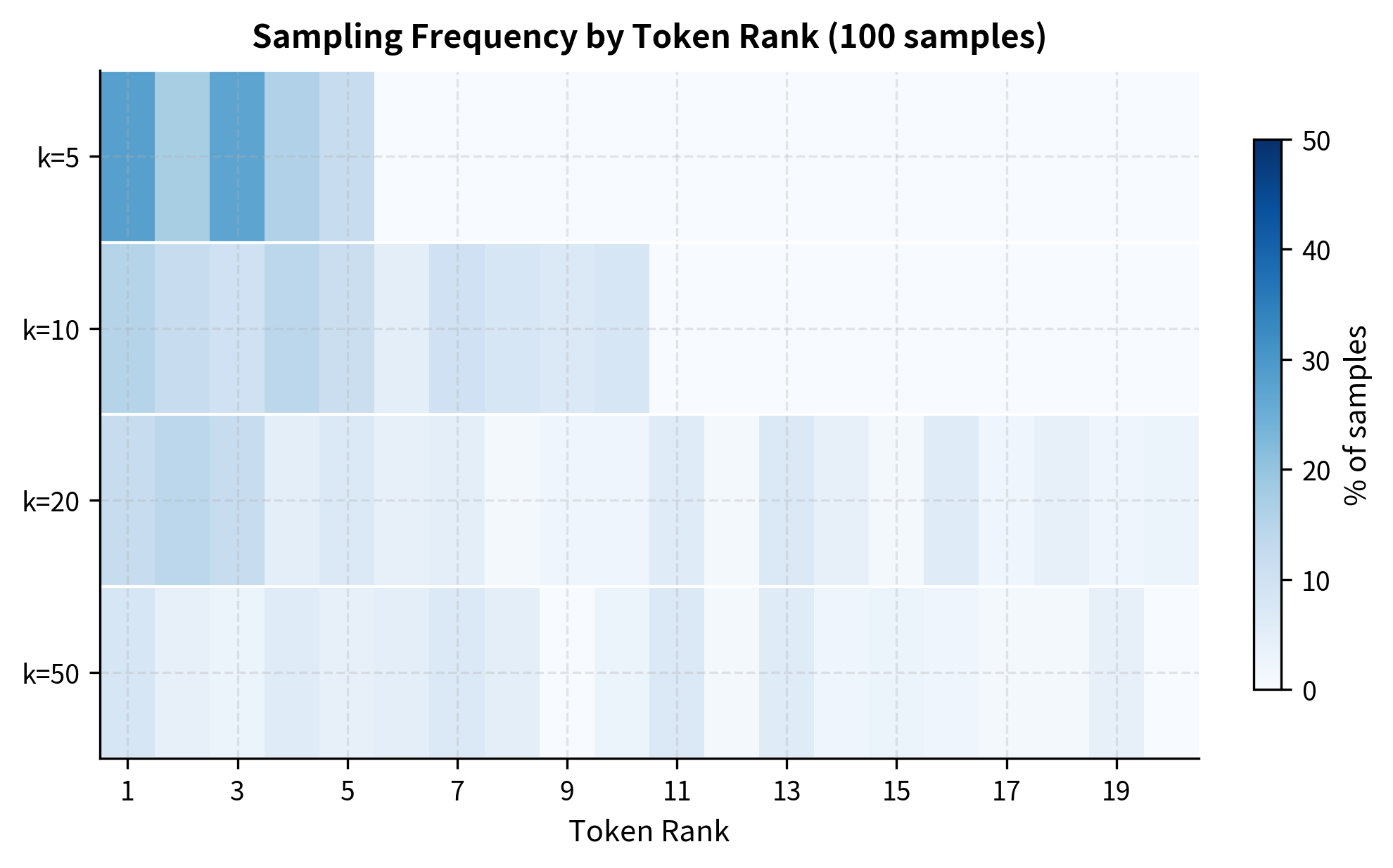
The heatmap reveals how shapes sampling behavior empirically. With , the dark cells concentrate in the leftmost columns, meaning the top-ranked tokens receive nearly all samples. As increases, the distribution spreads rightward, but higher-ranked tokens still dominate because they have higher probability even after renormalization.
Choosing the Right Value of k
The choice of significantly affects generation quality. There's no single optimal value, as the best depends on both the task and the context.
Guidelines for Selecting k
Consider these factors when choosing :
-
Task type: Creative writing benefits from higher (50-100) for variety. Factual responses work better with lower (10-30) for precision.
-
Context confidence: When the model is highly confident (one token dominates), even large won't introduce much diversity since top tokens have most of the mass anyway.
-
Generation length: Longer generations may need lower to prevent drift. Errors accumulate over many steps, and each improbable token can push the generation off course.
-
User expectations: Interactive applications often use =40-50 as a reasonable default that balances fluency with variety.
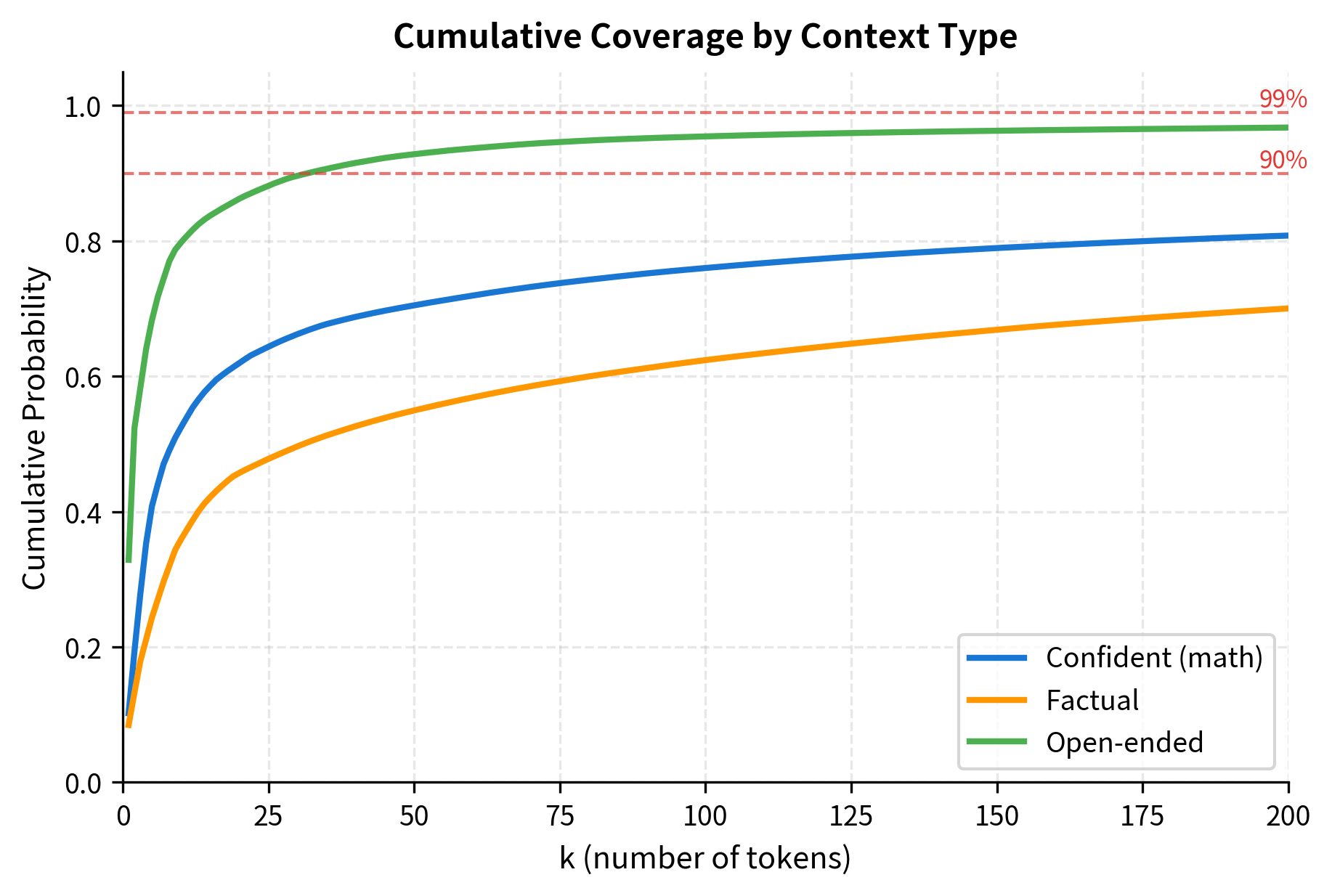
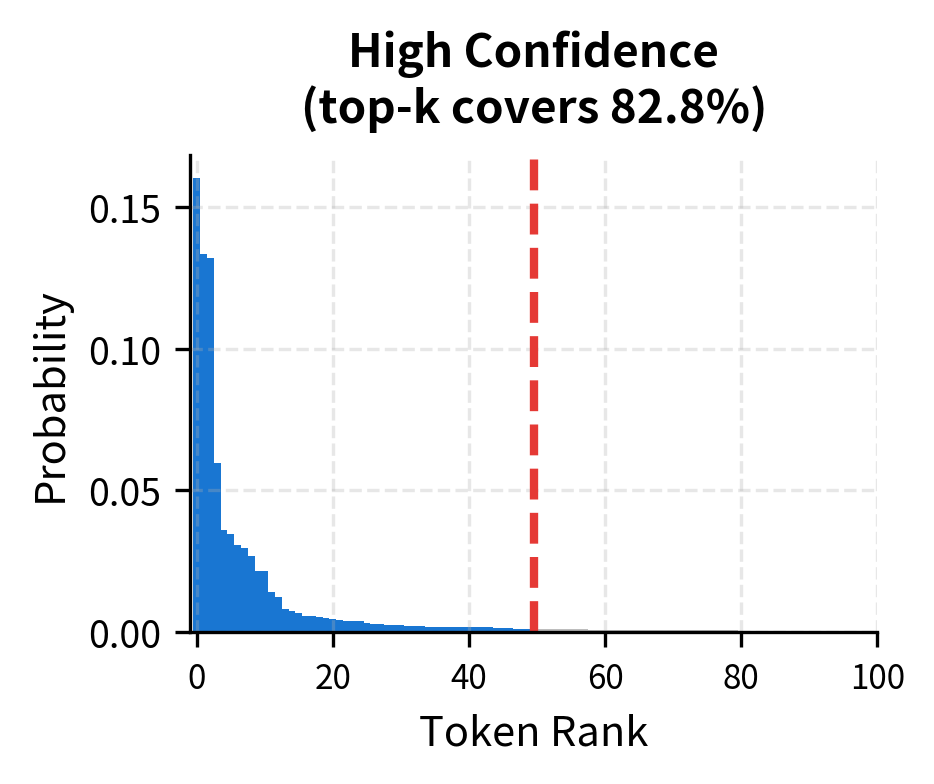
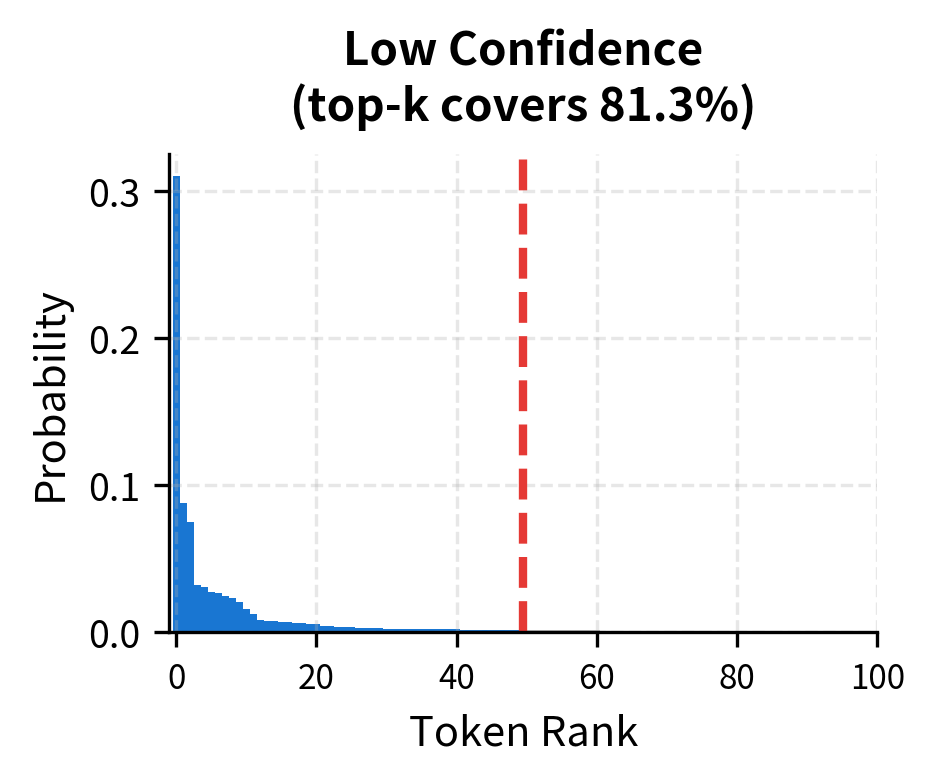
The coverage analysis reveals an important pattern: when the model is confident, a small captures most of the probability mass. "2 + 2 =" concentrates probability in very few tokens, so =10 might capture 99%+ of the mass. Open-ended prompts like "Once upon a time" spread probability more evenly, requiring larger to maintain diverse sampling.
This visualization makes the intuition concrete. For confident predictions like "2 + 2 =", the curve shoots up almost vertically, reaching 99% coverage with just a handful of tokens. Open-ended prompts show a gentler slope, requiring larger to achieve the same coverage. This explains why a fixed works differently across contexts.
Combining Top-k with Temperature
Top-k sampling and temperature scaling complement each other. Temperature adjusts the shape of the distribution before truncation, while top-k determines how many tokens to keep. Used together, they offer fine-grained control.
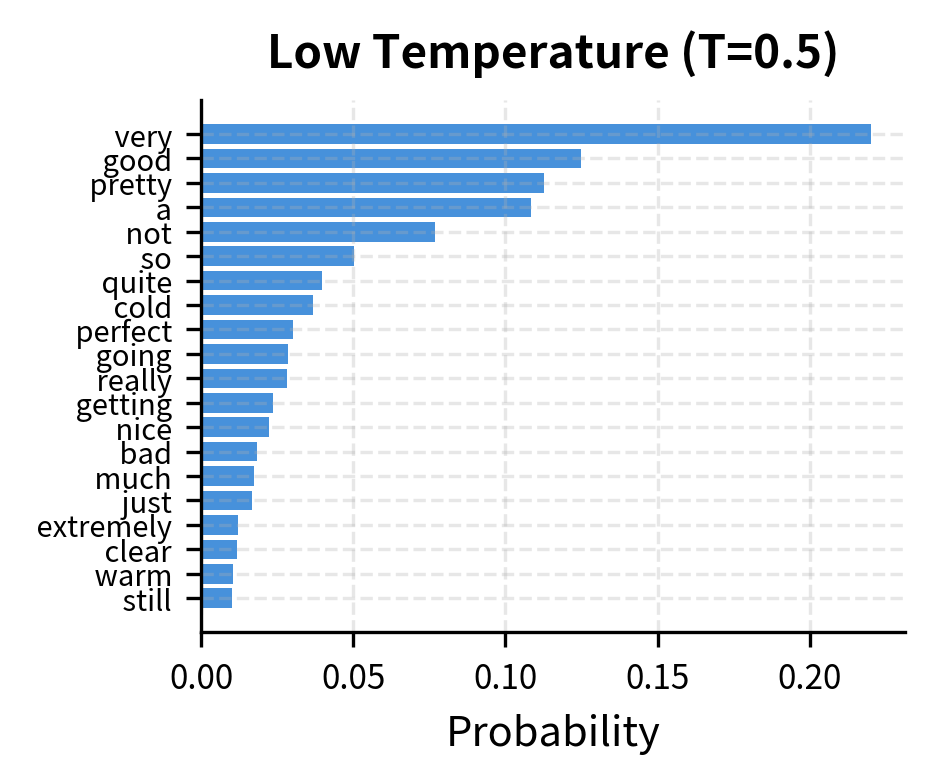
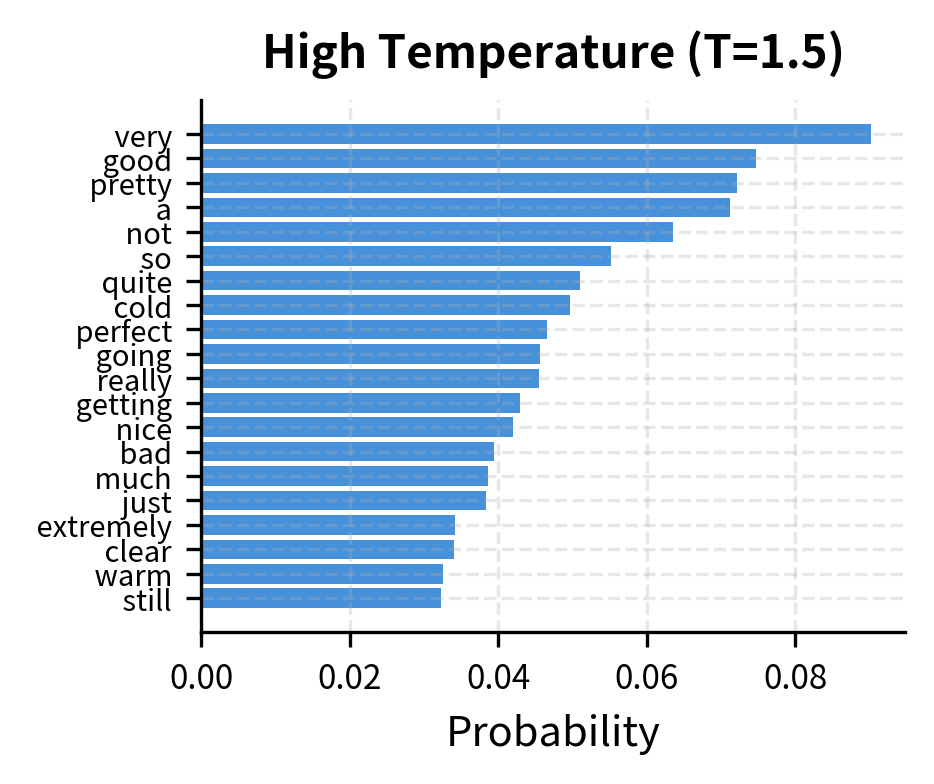
The figure shows how temperature reshapes the distribution within the top- candidates. At low temperature, the top token dominates even among the kept tokens. At high temperature, probability spreads more evenly across all tokens.
Temperature-First vs Top-k-First
The order of operations matters. Standard practice applies temperature first, then top-k:
- Temperature scaling: Divide logits by temperature
- Top-k selection: Keep the highest values
- Softmax: Convert to probabilities
- Sample: Draw from the truncated distribution
Why temperature first? Temperature affects which tokens qualify as "top-k". High temperature compresses differences between token probabilities, potentially changing which tokens make the cut. Low temperature exaggerates differences, making the ranking more pronounced. Applying temperature after top-k selection would mean truncating based on the original distribution, which may not match the sampling distribution you want.
The output shows that the top- tokens remain mostly stable across temperatures, with the highest-ranked tokens appearing in all lists. However, tokens near the boundary (rank 8-10) may swap in and out as temperature changes, which can subtly affect sampling behavior.
Practical Considerations
Moving from theory to production, several practical aspects affect how top-k sampling performs in real applications. This section covers computational efficiency, edge case handling, and batched generation.
Computational Efficiency
Top-k sampling adds minimal overhead to generation. The torch.topk operation is efficient, running in time, where is the vocabulary size and is the number of tokens to select. Since (typically is 50-100 while is 50,000+), this is essentially linear in vocabulary size.
The timings confirm that top-k selection takes only fractions of a millisecond, even for the largest values. Since a typical GPT-2 forward pass takes 10-50ms (and larger models take 100ms+), the top-k operation adds less than 1% overhead. This makes top-k sampling practical for production use without any performance concerns.
Handling Edge Cases
Several edge cases require attention in production implementations:
- k larger than vocabulary: If vocabulary size, top-k degenerates to full sampling
- All zero logits: Rare but possible with certain inputs; results in uniform sampling
- Very small k: =1 is equivalent to greedy decoding
Batched Generation
For efficiency with multiple sequences, top-k can be applied in parallel across a batch:
The batched implementation processes all four sequences in a single operation, returning one sampled token ID per sequence. This vectorized approach is essential for efficient inference when generating multiple sequences in parallel, as it avoids the overhead of looping through sequences individually.
Limitations of Top-k Sampling
While top-k is widely used, it has notable limitations that motivated the development of alternative approaches like nucleus (top-p) sampling.
Fixed k Ignores Context
The fundamental limitation is that is fixed regardless of context. Consider two scenarios:
- High-confidence context: "The president of the United States in 2020 was Donald", where very few tokens are reasonable next.
- Open-ended context: "I think the best way to", where many tokens could reasonably follow.
A fixed treats both identically. If =50, the first case includes many implausible tokens (the model might only need =5). The second case might benefit from even more options.
Quality-Diversity Trade-off
No single value works optimally across all situations. Lower improves quality but reduces diversity. Higher increases diversity but risks including low-quality tokens. This creates tension when the goal is both high quality and interesting variation.
The next chapter on nucleus sampling shows how adapting the truncation threshold to the probability distribution itself addresses these limitations.
Comparison with Other Decoding Methods
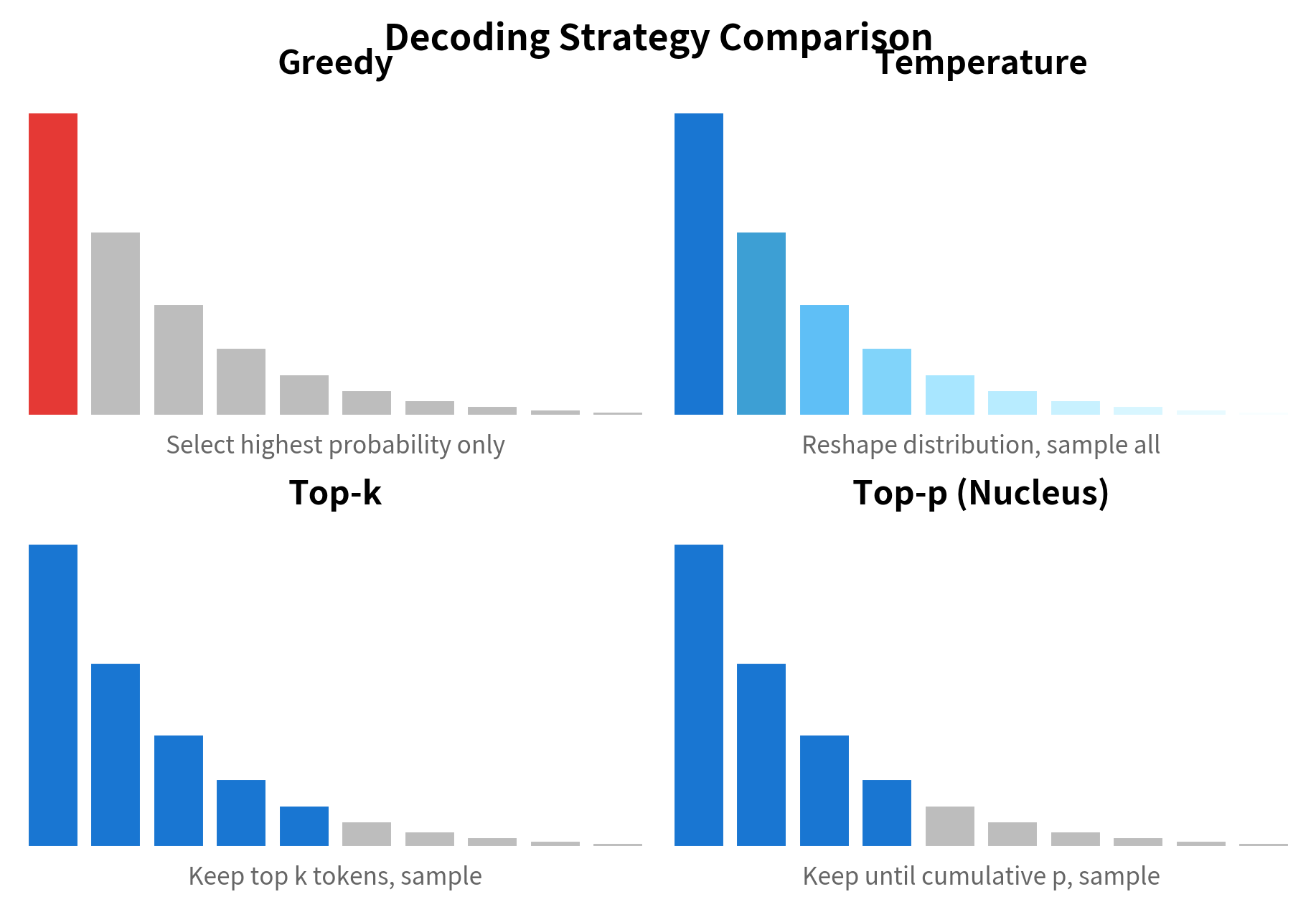
Let's compare top-k sampling with other decoding strategies to understand when each is most appropriate.
The comparison reveals characteristic differences. Greedy decoding produces focused but potentially repetitive text. Pure temperature sampling adds variety but can drift. Top-k restricts the sampling space while preserving diversity. Combining top-k with temperature offers the most control.
Key Parameters
When using top-k sampling for text generation, the following parameters have the greatest impact on output quality:
-
k (top_k): The number of highest-probability tokens to keep. Values of 40-100 work well for most applications. Lower values (10-30) produce more focused, deterministic output suited for factual content. Higher values (100-200) allow more creative diversity but risk occasional incoherent tokens.
-
temperature: Scales the logits before computing probabilities. Values below 1.0 sharpen the distribution, making the top tokens more dominant. Values above 1.0 flatten the distribution, spreading probability more evenly. Common values range from 0.7 to 1.2. Temperature is typically applied before top-k selection.
-
do_sample: Boolean flag in Hugging Face's
generate()method. Must beTrueto enable any sampling strategy including top-k. WhenFalse, the model uses greedy decoding regardless of other parameters. -
max_new_tokens: Limits the number of tokens to generate. Longer generations may accumulate sampling noise, so lower values can help maintain coherence over extended outputs.
Summary
Top-k sampling provides a practical solution to the long-tail problem in language model decoding. By truncating the vocabulary to the most likely tokens and renormalizing, it eliminates improbable tokens while preserving meaningful diversity among plausible choices.
Key takeaways from this chapter:
-
Truncation principle: Top-k zeros out all tokens outside the highest-probability candidates, then renormalizes the remaining probabilities. This prevents sampling from the incoherent long tail while allowing variety among reasonable options.
-
Temperature interaction: Temperature scaling reshapes the distribution before truncation. Low temperature concentrates probability in fewer tokens; high temperature spreads it more evenly. Applying temperature first affects which tokens make the top- cut.
-
Parameter selection: Common values range from =40 to =100. Lower produces more focused text; higher allows more diversity. The optimal choice depends on task, context confidence, and user preferences.
-
Fixed-k limitation: A constant applies regardless of context, including too many tokens when the model is confident and potentially too few when it's uncertain. This motivates adaptive approaches like nucleus sampling.
-
Computational efficiency: Top-k selection adds negligible overhead, with time complexity where is vocabulary size and is the number of tokens kept. This is fast compared to the model forward pass, making it practical for production use.
Top-k sampling strikes a useful balance between greedy decoding (deterministic but repetitive) and pure sampling (diverse but sometimes incoherent). While nucleus sampling offers more adaptive truncation, top-k remains widely used due to its simplicity and interpretability. The next chapter explores nucleus sampling, which addresses the fixed-k limitation by adapting the threshold to each distribution's shape.
Quiz
Ready to test your understanding? Take this quick quiz to reinforce what you've learned about top-k sampling and how it controls language model text generation.



Comments