Part of Language AI Handbook
Explains how temperature scaling reshapes probability distributions during text generation, with mathematical foundations, implementation details.
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Article links
Make inline references clickable
Decoding Temperature
When a language model predicts the next token, it does not simply look up the correct answer in a table. It produces a full probability distribution over its entire vocabulary, every single word and subword it has ever encountered during training. Given the prompt "The capital of France is," the model might assign 0.85 to "Paris," 0.05 to "Lyon," 0.02 to "Marseille," and tiny probabilities to thousands of other tokens. That distribution encodes everything the model learned during training: the frequencies of words, the syntactic patterns of sentences, the semantic constraints of meaning. Temperature is the parameter that controls how we interpret and sample from this distribution at generation time.
Temperature answers a basic question: how much should we trust the model's probability rankings? A temperature of 1.0 preserves the learned distribution exactly, sampling from it just as the model's training implied. Lower temperatures sharpen the distribution, making high-probability tokens even more likely and pushing the model toward deterministic, predictable output. Higher temperatures flatten the distribution, giving lower-probability tokens a fighting chance and introducing creative variability. This single scalar parameter is, remarkably, one of the most important controls practitioners have over language model behavior.
Think of temperature as a confidence dial. At one extreme, you tell the model to always go with its gut, committing to whichever continuation it found most plausible. At the other extreme, you tell the model to treat all of its guesses as equally valid and pick one at random. In between lies a continuous spectrum of behaviors: cautious and factual at the low end, expressive and exploratory at the high end. No other single parameter gives you quite this direct a handle on the randomness of generation. Unlike architectural choices or fine-tuning procedures, temperature is a real-time knob you can adjust on every inference call.
Understanding temperature matters for both practitioners who deploy language models and researchers who study them. If you are building a factual question-answering system, temperature near zero ensures you get the most probable (and often most accurate) answer without unnecessary variability. If you are building a creative writing assistant, moderate temperature is what separates outputs that feel alive from outputs that feel like template completions. And if you are studying how language models generalize, temperature provides a window into the shape of the probability distributions they have learned. A model with well-calibrated logits will produce coherent outputs across a wide range of temperatures; a poorly calibrated model may degrade rapidly.
This chapter explores temperature from first principles. You will learn the mathematical mechanics of temperature scaling, visualize how it reshapes probability distributions, implement temperature-controlled sampling, and develop intuition for selecting appropriate values across different generation tasks. By the end, you will understand how to set the temperature knob, why changing it has the effects it does, and when those effects are beneficial versus harmful.
How Temperature Scaling Works
To understand temperature, we need to start with what language models output. When you feed a prompt into a model, the final linear layer does not produce probabilities directly. Instead, it outputs a vector of logits: raw, unbounded scores for every token in the vocabulary. A logit of 5.0 does not mean "5% probability." It is just a score showing relative preference. The token with the highest logit is the model's top choice, but we need a way to convert these scores into actual probabilities we can sample from.
The distinction between logits and probabilities matters a great deal in practice. Because logits are unbounded, they can be negative, very large, or very small. A logit of 10.0 and a logit of -5.0 exist on the same scale, but the absolute values carry no direct probabilistic meaning. Only the differences between logits are semantically meaningful: a logit difference of 5.0 means the model prefers one token over another by a certain degree, but by how much in probability terms depends on all the other logits in the vocabulary. This is why the normalization step is needed.
The final linear layer of a transformer language model produces these logits through a simple matrix multiplication: the hidden state vector at the last token position is multiplied by a weight matrix of shape (hidden dimension, vocabulary size). This produces one scalar per token in the vocabulary, representing how strongly the model's learned representation activates each output class. Because the weight matrix is unconstrained, the logits can take any real value, and they carry no built-in probabilistic interpretation until we apply softmax.
Here the softmax function enters the picture. Softmax takes a vector of arbitrary real numbers and turns them into a valid probability distribution: all values become positive and sum to exactly 1. The key mechanism is exponentiation: taking the exponential of each logit makes all values positive (since for any ), and then dividing by the sum of all exponentiated values normalizes them into probabilities. For a vocabulary of tokens with logits , the standard softmax computes:
where:
- : the logit for token , which can be any real number
- : the exponential function applied to the logit, so the result is positive regardless of the sign of
- : the sum of all exponentiated logits across the full vocabulary, serving as a normalizing constant that ensures the output probabilities sum to 1
Why does this formula make sense? Notice that exponentiation is a monotone increasing function: if , then . This means the ordering of preferences is preserved: the token with the highest logit still gets the highest probability. The exponential also amplifies differences: a logit that is 1.0 higher than another gets times more probability mass before normalization. This amplification is what makes softmax sensitive to logit differences, which is exactly the property that temperature will manipulate.
The left panel shows raw logits: a descending sequence of numbers from 3.2 down to 0.3. These numbers are the direct output of the model's final linear layer and have no probabilistic interpretation on their own. The right panel shows what happens after softmax: the top token, "sunny," captures about 32% of the probability mass, while "unpredictable" at the bottom receives only about 2%. Notice that the logit difference between "sunny" (3.2) and "cloudy" (2.8) is just 0.4, yet softmax converts this into a meaningful gap in probability. The model prefers "sunny" by a factor of relative to "cloudy," which becomes visible in the probability bars.
But here is the problem: the standard softmax gives us exactly one distribution. It reflects whatever probability concentrations the model learned during training. What if we want more control? What if the model's top choice is good but we want to explore alternatives? Or conversely, what if we want to make the model more decisive, committing more strongly to its best guess? The model's learned distribution is fixed at inference time, but we are free to transform it before sampling.
Introducing the Temperature Parameter
Temperature gives us that control. The idea is elegantly simple: before applying softmax, we divide all logits by a temperature parameter . This single modification lets us reshape the entire probability distribution without changing the model's weights or the ordering of its preferences. All we are doing is rescaling the inputs to the softmax function, which changes how sharply it distinguishes between high-logit and low-logit tokens.
Temperature scaling divides the logits by a temperature parameter before computing the softmax. Given logits for vocabulary token , the temperature-scaled probability is:
where:
- : the logit (raw score) for token output by the model's final layer
- : the temperature parameter, a positive scalar that controls distribution sharpness
- : the exponential of the scaled logit, which ensures positive values
- : the sum over all tokens in the vocabulary, serving as a normalizing constant
When , this reduces to the standard softmax. When , dividing by a fraction amplifies the logit differences. When , dividing by a larger number compresses the differences.
Why does this formula make sense? Notice that dividing by is equivalent to multiplying the entire logit vector by before softmax. When , the factor , so every logit gets scaled up. But because softmax only cares about differences between logits, the effect is to amplify those differences. When , the factor , so differences shrink. The normalization ensures the output still sums to 1 regardless of .
The name "temperature" comes from statistical mechanics, where a similar parameter controls the randomness of particle states in a physical system. At low temperature, particles settle into their lowest-energy states, creating a highly ordered, predictable configuration. At high temperature, particles have enough thermal energy to explore many states more freely, creating a more disordered, random configuration. The analogy carries over perfectly to language models: low temperature means the model commits to its top choices; high temperature means it explores more freely across the vocabulary. Think of temperature as the amount of "creative heat" you are injecting into the generation process.
Temperature scaling has its roots in the Boltzmann distribution from statistical mechanics, named after physicist Ludwig Boltzmann. In that context, the probability of a system occupying a state with energy at absolute temperature is proportional to , where is the Boltzmann constant. At low temperatures, systems overwhelmingly occupy low-energy states; at high temperatures, higher-energy states become accessible.
The connection to language models was made explicit in the 1980s through work on Boltzmann machines, a class of stochastic neural networks where temperature controlled the probability of neuron activations. Geoffrey Hinton and Terry Sejnowski introduced the idea of annealing the temperature during training, starting high (random exploration) and cooling down (committing to good solutions). This technique, called simulated annealing, was borrowed from metallurgy, where controlled cooling of metals produces stronger crystal structures.
When softmax-based language models arrived in the 1990s and 2000s, the temperature parameter transferred naturally. The connection to the Boltzmann distribution is not merely metaphorical: the softmax function with a temperature parameter is mathematically identical to the Boltzmann distribution if you interpret the logits as negative energies. This deep connection between statistical mechanics and neural network training explains why "temperature" became the canonical term for this parameter.
A Concrete Example: Three Candidate Tokens
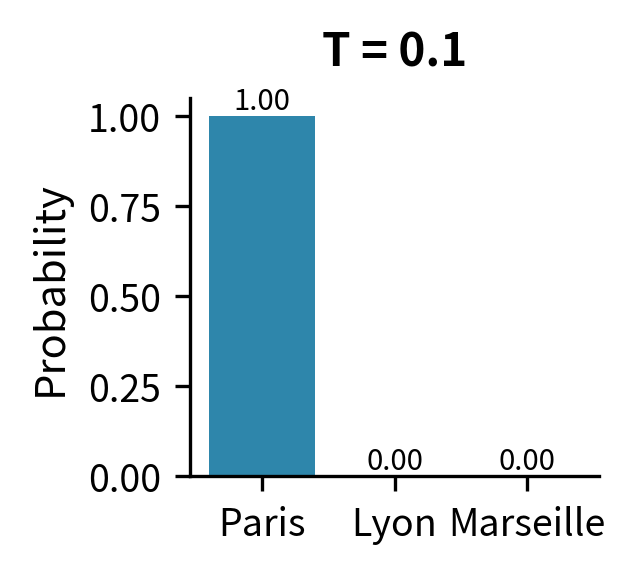
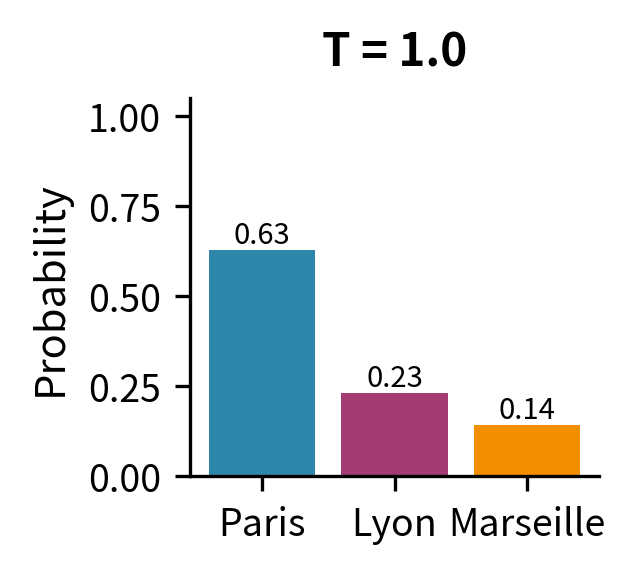
Let's make this concrete. Suppose a language model is completing the prompt "The capital of France is" and has narrowed down to three plausible tokens: "Paris," "Lyon," and "Marseille." The model outputs logits of 2.0, 1.0, and 0.5 respectively. Paris has the highest logit, so it is the model's top choice, but how do the probabilities change as we vary temperature?
# Example logits for three tokens
logits = torch.tensor([2.0, 1.0, 0.5])
tokens = ["Paris", "Lyon", "Marseille"]
def temperature_softmax(
logits: torch.Tensor, temperature: float
) -> torch.Tensor:
"""Apply temperature scaling and compute softmax."""
scaled_logits = logits / temperature
return F.softmax(scaled_logits, dim=0)Token probabilities at different temperatures: Token T=0.5 T=1.0 T=2.0 --------------------------------------------- Paris 0.844 0.629 0.481 Lyon 0.114 0.231 0.292 Marseille 0.042 0.140 0.227
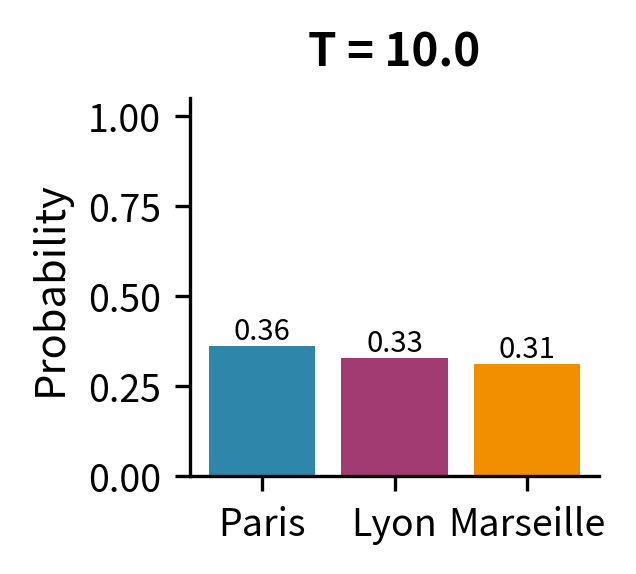
The results reveal temperature's effect clearly. At , "Paris" dominates with roughly 84% probability, leaving only scraps for the alternatives. The model is highly confident, almost deterministic. At (standard softmax), we get the baseline distribution: Paris around 59%, Lyon around 22%, Marseille around 13%. The model still prefers Paris but gives meaningful weight to alternatives. At , the distribution flattens dramatically: Paris drops toward 39%, and even Marseille climbs toward 22%. The model is now much more willing to sample less-preferred tokens.
The point is that the ordering of probabilities is preserved across all temperatures. Paris is always the most likely token, Lyon is always second, and Marseille is always third. Temperature does not change which tokens are preferred; it only changes how strongly the preferences are expressed. This is a important property: you are not distorting the model's knowledge when you adjust temperature, you are only adjusting how decisively it acts on that knowledge. This preservation of rank ordering is what makes temperature a principled intervention rather than arbitrary noise injection.
The Mathematics of Sharpening and Flattening
Why does this simple division produce such dramatic effects? The key insight comes from examining how temperature affects the probability ratio between any two tokens. Understanding this ratio reveals the core mechanism at work.
Consider two tokens with logits and , where (token 1 is preferred). Under temperature scaling, their probabilities are computed separately but share the same normalization constant. We can compute the ratio to understand how much more likely token 1 is compared to token 2:
When we compute the ratio , something beautiful happens: the normalization constants cancel out completely:
where:
- : the logit gap between the two tokens, representing how much more the model prefers token 1
- : temperature, which scales how strongly this preference translates to a probability ratio
- : the exponential function, which converts the scaled difference to a multiplicative ratio
This formula is the key to understanding temperature. The effective logit gap becomes . Temperature acts as a divisor on the gap itself, not on the probabilities directly. The probability ratio between any two tokens is governed entirely by their logit difference and the temperature, independent of all other tokens in the vocabulary.
When , we divide the gap by a fraction, which amplifies it. A logit difference of 1.0 at becomes an effective difference of . The exponential of 2.0 is about 7.4, so the preferred token becomes 7.4 times more likely than its competitor. The distribution sharpens dramatically.
When , we divide the gap by a number greater than 1, which compresses it. The same logit difference of 1.0 at becomes an effective difference of . The exponential of 0.5 is about 1.65, so the preferred token is only 1.65 times more likely. The distribution flattens substantially. Notice that a token that was 2.72 times more likely at (the baseline) compresses to just 1.65 times more likely at : a significant change in behavior from a modest parameter adjustment.
An important consequence of this ratio formula is that temperature affects all token pairs simultaneously and by the same multiplicative factor. If the ratio between token A and token B is multiplied by when temperature changes, the ratio between token C and token D is also multiplied by (adjusted for the difference in their logit gaps). This uniformity is both a feature and a limitation: it produces simple, predictable behavior but cannot be tailored to treat different vocabulary regions differently.
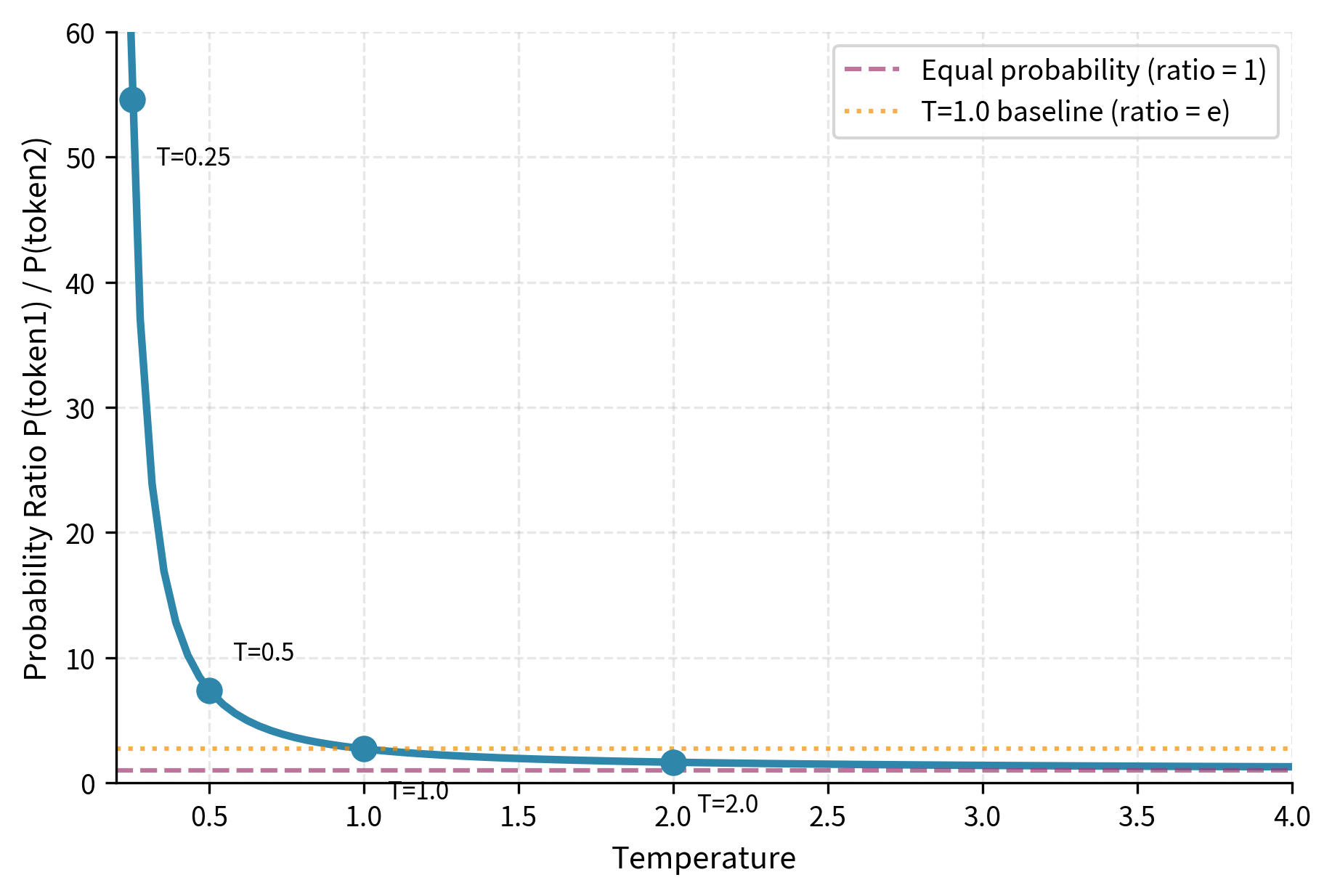
Let's verify this with actual calculations:
def probability_ratio(z1: float, z2: float, temperature: float) -> float:
"""Compute probability ratio between two tokens given their logits."""
return np.exp((z1 - z2) / temperature)
# Logit gap of 1.0 between tokens
z1, z2 = 2.0, 1.0Probability ratio (P(token1) / P(token2)) at different temperatures: T = 0.25: ratio = 54.60 T = 0.5 : ratio = 7.39 T = 1.0 : ratio = 2.72 T = 2.0 : ratio = 1.65 T = 4.0 : ratio = 1.28
The numbers tell the story. At , the higher-probability token is 55 times more likely than its competitor, an overwhelming advantage. At (baseline), the ratio is 2.72 (which is just , exactly as the formula predicts). At , that ratio shrinks to just 1.28, meaning the two tokens are nearly equally likely despite the original logit gap. Temperature truly acts as a dial between certainty and randomness.
Temperature Extremes: The Limiting Cases
To build complete intuition, consider what happens at the mathematical extremes. These limiting cases are never exactly achievable but reveal the asymptotic behavior of temperature scaling.
As (approaching zero):
The effective logit gap grows without bound for any non-zero gap. The exponential of infinity is infinity, so the probability ratio between the top token and any other token becomes infinite. In practice, this means all probability mass concentrates on the single highest-logit token. This limiting case is equivalent to greedy decoding or argmax selection: always pick the most likely token, with zero randomness. Think of it as a model that has become infinitely confident in its first guess, never entertaining any alternative.
Greedy decoding has a specific failure mode worth understanding: repetition loops. If the model is in a context where a particular phrase is highly probable, greedy decoding will produce that phrase deterministically, and because the phrase is now part of the context, the same phrase becomes highly probable again. The result is the infamous "degenerate repetition" problem: "The cat sat on the mat. The cat sat on the mat. The cat sat on the mat." A small positive temperature (0.1 to 0.3) typically eliminates this problem while preserving most of the benefits of low-temperature generation.
As (approaching infinity):
The effective logit gap shrinks toward zero for any finite gap. The exponential of zero is 1, so the probability ratio between any two tokens approaches 1:1. All tokens become equally likely regardless of their original logits. The distribution approaches uniform, and generation becomes pure random sampling from the vocabulary. Think of it as a model that has forgotten everything it learned, selecting tokens as if by rolling a many-sided die.
Neither extreme is useful for text generation. produces repetitive, predictable text that lacks nuance. The model keeps selecting the same high-probability continuations, often getting stuck in loops where the same phrases repeat endlessly. produces incoherent gibberish since token selection ignores the model's learned preferences entirely. The resulting text looks like random strings drawn from a vocabulary distribution, violating every grammatical and semantic constraint the model learned during training. Practical values fall between these extremes, typically in the range 0.1 to 2.0.
The visualization makes the extremes clear. At , Paris captures nearly all of the probability mass. This leaves virtually nothing for alternatives. The generation outcome is essentially predetermined before any randomness is applied. At , the three tokens have nearly equal probability. It approaches the uniform distribution of 33.3% each. If you sampled many tokens at this temperature, you would sample each of the three cities with roughly equal frequency, which is obviously not the behavior you want for a factual geography question. The standard softmax at sits in between. This reflects the model's learned preferences while still letting meaningful sampling diversity.
Visualizing Temperature Effects
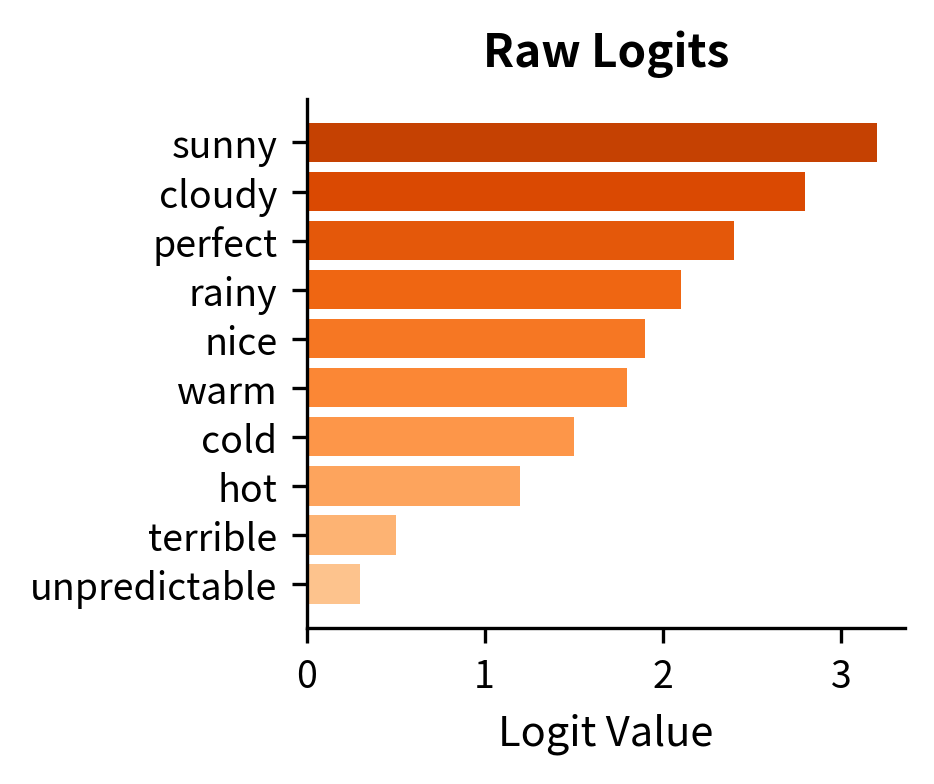
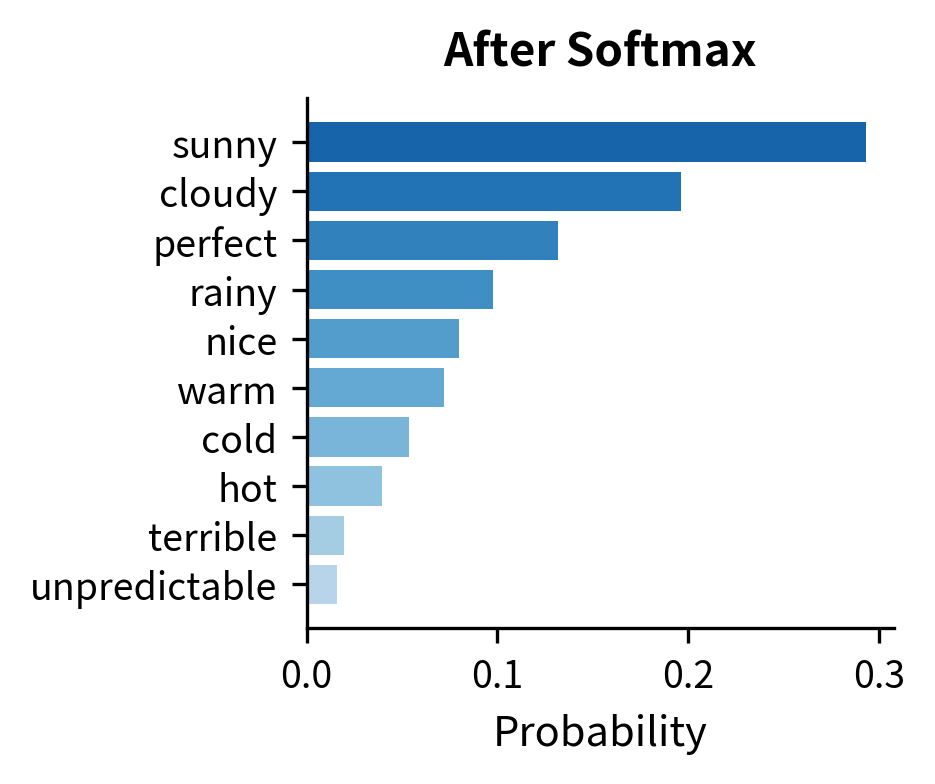
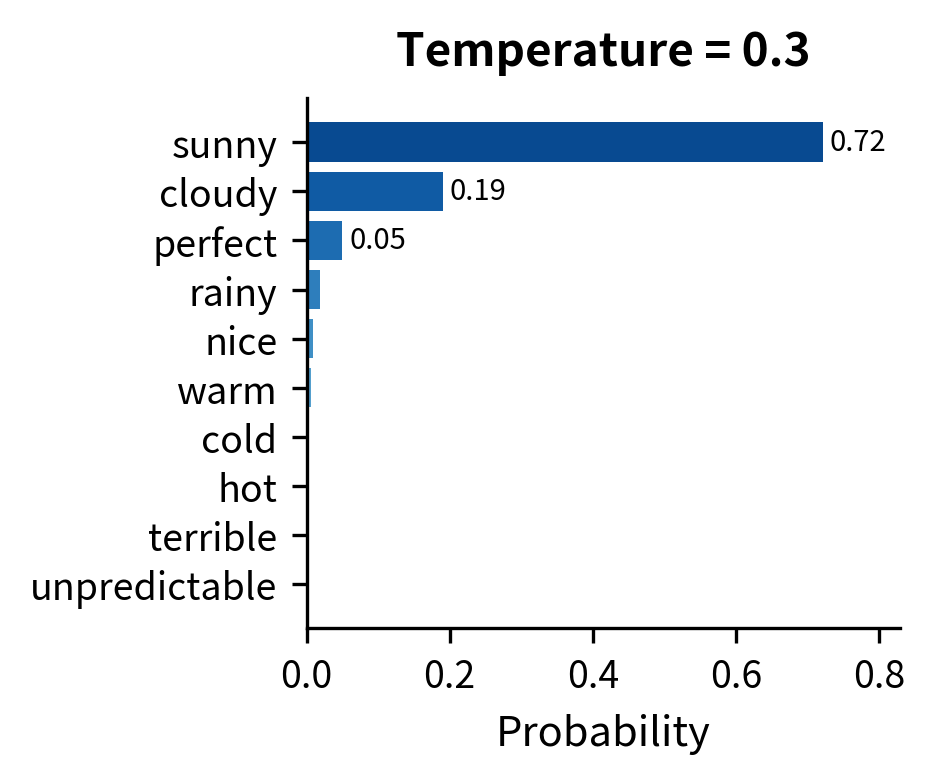
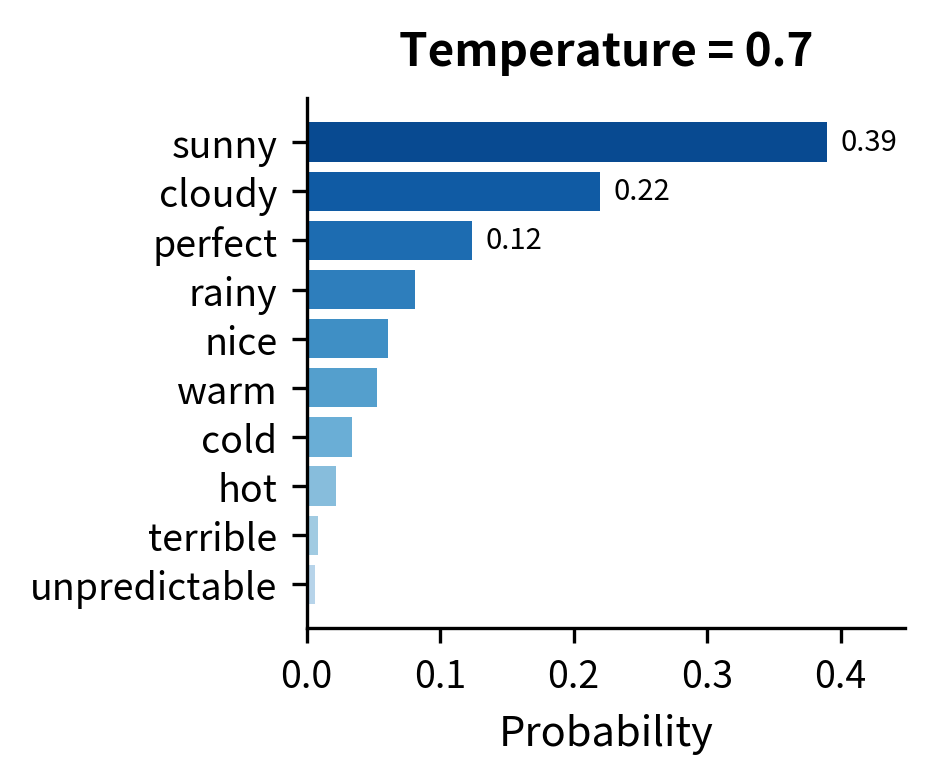
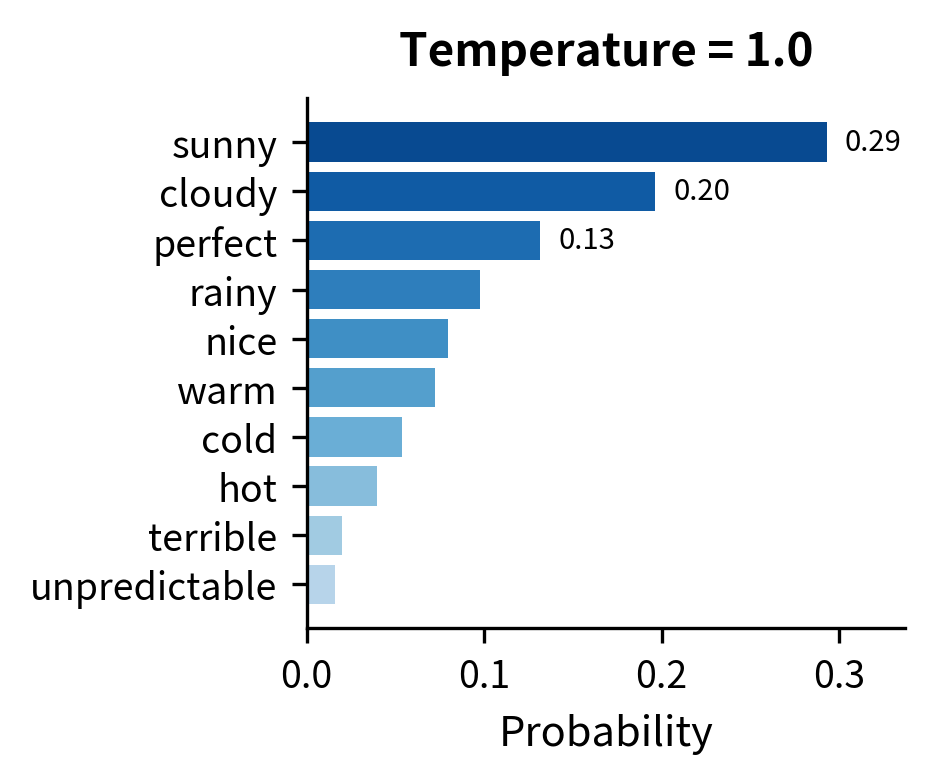
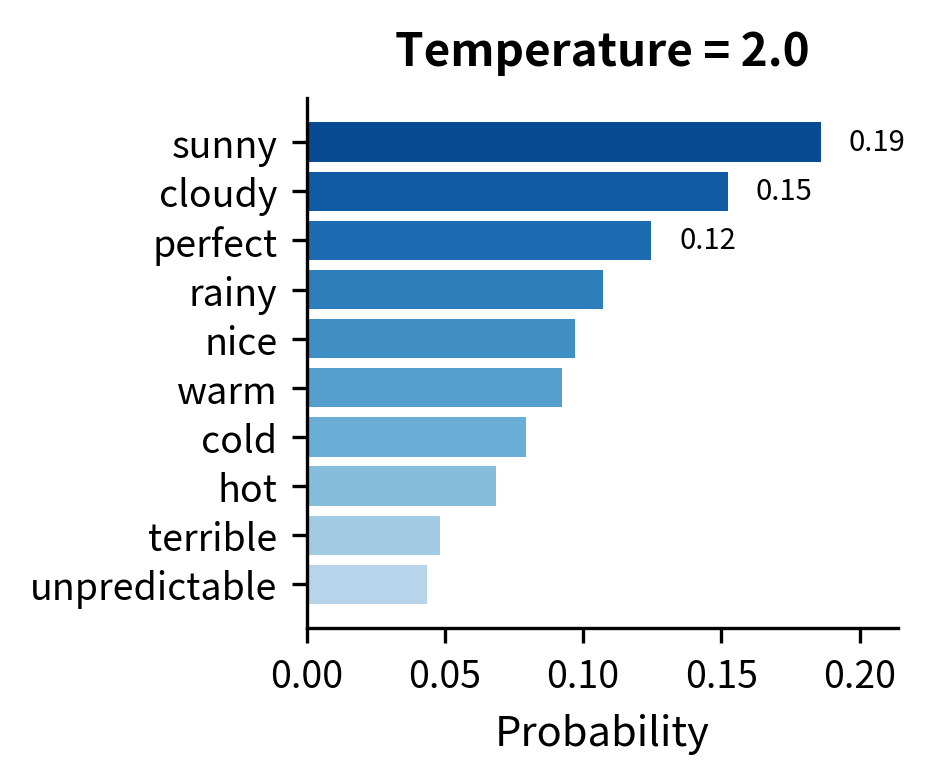
To develop intuition for temperature, let's visualize how it reshapes a realistic probability distribution. We will simulate logits from a language model predicting the next token after "The weather today is" and examine distributions across a range of temperatures. This section gives you a feel for the continuous nature of temperature's effect, rather than just discrete snapshots.
A single number like can feel abstract. What makes temperature intuition concrete is seeing the full distribution shift as changes. You will notice that some tokens barely change their relative rank while others experience dramatic swings in their probability. Tokens in the middle of the logit range are most affected: the very top tokens at low temperature already capture nearly all probability, so there is little room to grow, and the very bottom tokens are so far down the distribution that even high temperature cannot lift them to meaningful probabilities.
The redistribution of probability under temperature also has an important implication for generation diversity. When you double the temperature, you do not simply add a fixed amount of probability to each low-ranked token. Instead, you proportionally adjust the ratios between all token pairs. Tokens that were already close together in logit value (say, logit difference of 0.1) end up nearly equal in probability at any non-extreme temperature. Tokens far apart in logit value (say, logit difference of 3.0) remain unequal across a wide range of temperatures. This means the "effective vocabulary" from which sampling draws grows nonlinearly with temperature.
# Simulate logits for a vocabulary of plausible next tokens
vocab = [
"sunny",
"cloudy",
"rainy",
"nice",
"terrible",
"cold",
"warm",
"hot",
"perfect",
"unpredictable",
]
# Logits which reflects different likelihoods
logits_weather = torch.tensor(
[
3.2, # sunny - most likely
2.8, # cloudy
2.1, # rainy
1.9, # nice
0.5, # terrible
1.5, # cold
1.8, # warm
1.2, # hot
2.4, # perfect
0.3, # unpredictable
]
)
At , "sunny" captures over 60% of the probability mass, leaving little room for alternatives. This produces predictable text but misses the natural variation in language. Most weather descriptions do not use "sunny" as frequently as this distribution implies. At , the top five tokens each have between 10% and 18% probability. Sampling here introduces meaningful diversity while still favoring contextually appropriate completions. Notice that even "terrible" and "unpredictable," which had the lowest logits, receive non-trivial probabilities at , which could produce interesting creative writing but problematic factual generation.
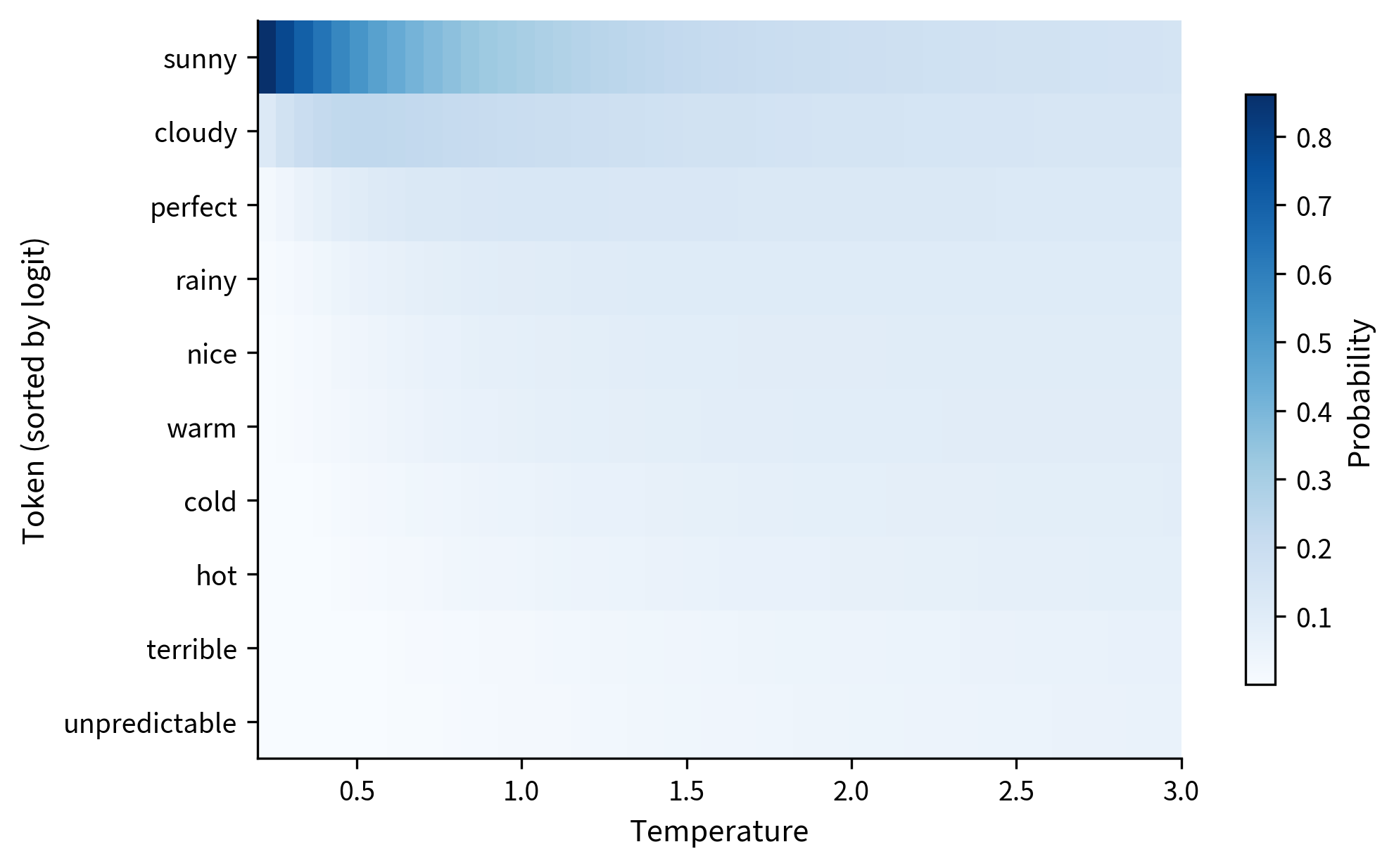
A heatmap reveals the continuous transformation more clearly. Each row shows one token's probability as temperature varies from left (low , sharp distribution) to right (high , flat distribution). Watching a single row across the heatmap shows you exactly how that token's fate changes with temperature:
The heatmap shows the redistribution of probability mass. At low temperature, the top token ("sunny") absorbs most probability (dark band at top-left). As temperature increases, probability spreads more evenly across all tokens (lighter, more uniform coloring toward the right). The transition is not abrupt but smooth and continuous. Tokens that start with low probabilities (bottom rows) gain probability slowly at first, then more rapidly as temperature increases.
Entropy and Temperature
Entropy quantifies the uncertainty or "spread" of a probability distribution. A distribution that assigns all probability to a single token has zero uncertainty: we know exactly what will be sampled. A distribution that assigns equal probability to all tokens has maximum uncertainty: every outcome is equally surprising. Shannon entropy gives this intuition a precise mathematical form.
For a discrete distribution over tokens, Shannon entropy measures the average number of bits of information in a random draw. It is computed as:
where:
- : the entropy of distribution , measured in bits
- : the probability of token
- : logarithm base 2, so entropy is measured in bits
- The negative sign ensures entropy is positive, since of a probability between 0 and 1 is negative
Why does this formula make sense? Consider the term : this is the surprise of observing token . A very likely token () has near-zero surprise, while a very unlikely token () has enormous surprise. Entropy is the probability-weighted average surprise across all tokens, measuring how surprised we expect to be, on average, when we sample from the distribution. A high-entropy distribution contains more "information" in each sample because samples are harder to predict.
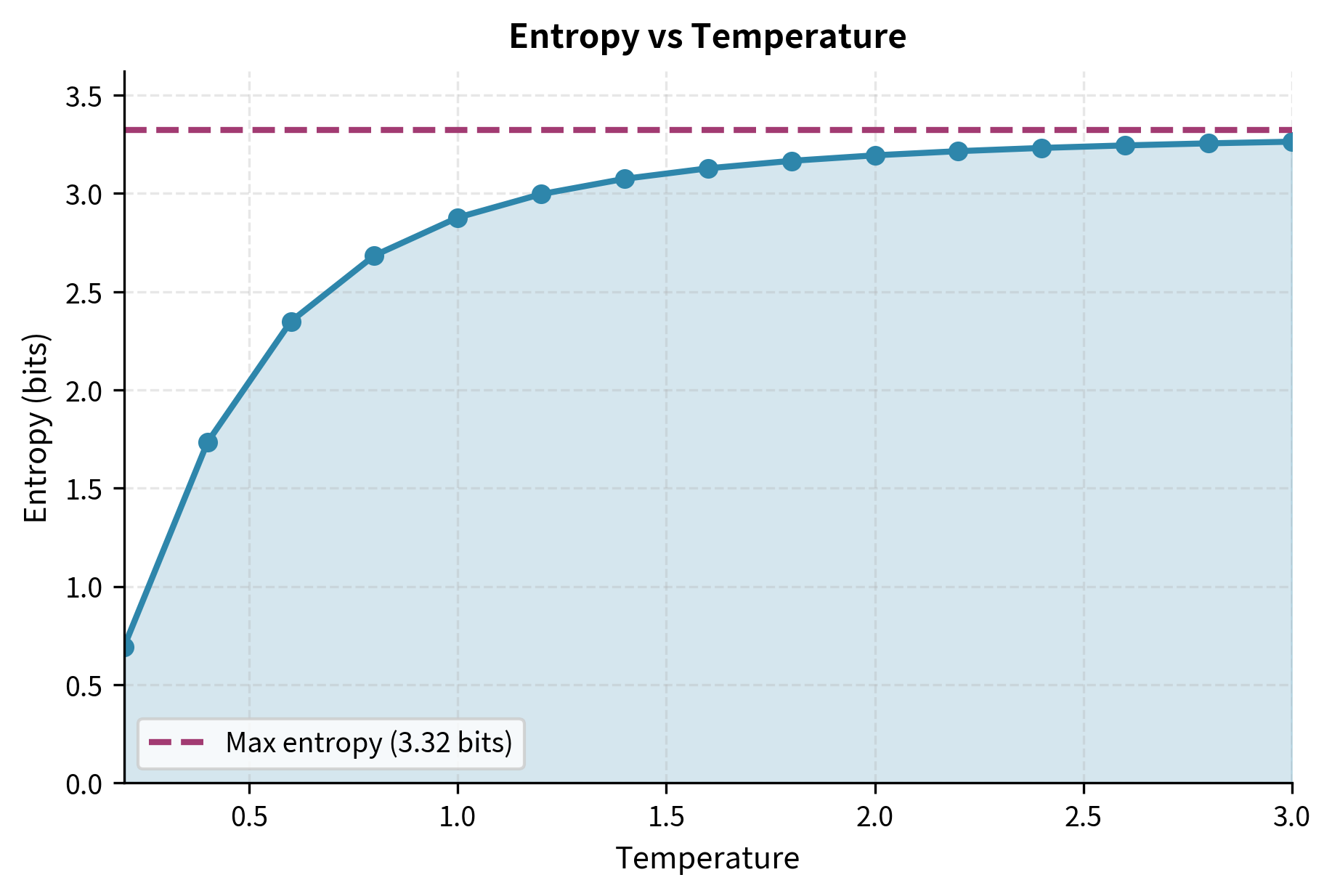
Entropy has intuitive extremes. When one token has probability 1.0 and all others have 0, entropy equals 0 bits: no uncertainty at all. When all tokens are equally likely with probability , entropy reaches its maximum of bits, which for a vocabulary of 10 tokens is bits.
Temperature directly controls entropy. Low temperature concentrates probability mass on high-logit tokens, reducing entropy and predictability. High temperature spreads probability more evenly, increasing entropy toward the maximum. The relationship between temperature and entropy is monotonically increasing: any increase in temperature (for the same set of logits) increases entropy. This means you can think of temperature as a direct entropy control: set to the level of uncertainty you want the model to exhibit at each generation step.
The entropy connection also explains why extremely high temperatures cause qualitative degradation in output. When entropy approaches where is the full vocabulary size of 50,000+ tokens, you are essentially sampling from a uniform distribution over the entire vocabulary. A 50,000-sided die produces tokens with no semantic relationship to the context. Real coherent text has low entropy at most positions: given a sentence like "The dog chased the," the next word is very constrained (nouns or pronouns, probably animate, probably syntactically appropriate), and the true distribution has entropy of perhaps 2 to 4 bits out of a possible 15+ bits for the full vocabulary.
def compute_entropy(probs: torch.Tensor) -> float:
"""Compute Shannon entropy of a probability distribution."""
# Filter out zero probabilities to avoid log(0)
probs = probs[probs > 0]
return -(probs * torch.log2(probs)).sum().item()Temperature vs Entropy: Temperature Entropy (bits) --------------------------- 0.3 0.693 0.5 1.733 1.0 2.877 1.5 3.127 2.0 3.214 3.0 3.262 Maximum possible entropy (uniform): 3.322 bits
With 10 tokens in our vocabulary, maximum entropy (achieved when the distribution is uniform) is bits. At , entropy drops to around 1.5 bits, showing the distribution is highly concentrated on just a few tokens. At , entropy approaches 3 bits, nearly matching the uniform distribution's maximum uncertainty. Each additional bit of entropy roughly doubles the effective number of tokens that receive meaningful probability mass.
Worked Example: Step-by-Step Temperature Calculation
Before implementing temperature in a full generation loop, let's walk through a complete numerical example from raw logits to sampled token. This trace is the kind of calculation that happens millions of times during a single generation call: once per token position, across every possible token in the vocabulary.
Suppose our model has just processed the prompt "The weather in Paris is" and the final linear layer has output the following logits for five candidate tokens:
- "beautiful": 3.5
- "rainy": 2.0
- "cold": 1.8
- "unusual": 0.9
- "enormous": -0.5
We will apply temperature and trace every step.
Step 1: Divide all logits by the temperature.
Notice that the logit differences have all been amplified by a factor of . The gap between "beautiful" and "rainy" was in the original logits, and now it is in the scaled logits.
Step 2: Exponentiate the scaled logits.
Step 3: Compute the normalization constant (denominator).
Step 4: Divide each exponentiated value by to get probabilities.
Step 5: Verify that probabilities sum to 1.
The small rounding error is expected; exact computation would give exactly 1.0.
Step 6: Sample from the distribution.
We now draw one token index according to these probabilities. With , "beautiful" has an 81.1% chance of being selected. If we had used instead, the probability of "beautiful" would be lower, and "rainy" and "cold" would have had more of a fighting chance. The temperature has sharpened the distribution, amplifying the model's confidence in "beautiful" beyond what the raw logits at would have implied. Notice that "enormous" has only a 0.3% chance: semantically, "The weather in Paris is enormous" is nonsensical, and the model's logits correctly reflect this, assigning a strongly negative logit. Even at , the probability of "enormous" would only rise to about 2%: a sensible result.
Let's confirm these calculations with code:
# Numerical trace of temperature scaling
example_tokens_trace = ["beautiful", "rainy", "cold", "unusual", "enormous"]
example_logits_trace = torch.tensor([3.5, 2.0, 1.8, 0.9, -0.5])
T_trace = 0.7Step 1: Scaled logits (z_i / T): beautiful : 3.50 / 0.7 = 5.000 rainy : 2.00 / 0.7 = 2.857 cold : 1.80 / 0.7 = 2.571 unusual : 0.90 / 0.7 = 1.286 enormous : -0.50 / 0.7 = -0.714 Step 2: Exponentiated (exp(z_i / T)): beautiful : 148.413 rainy : 17.412 cold : 13.085 unusual : 3.617 enormous : 0.490 Step 3: Normalization constant Z = 183.016 Step 4: Final probabilities: beautiful : 0.8109 (81.1%) rainy : 0.0951 (9.5%) cold : 0.0715 (7.1%) unusual : 0.0198 (2.0%) enormous : 0.0027 (0.3%) Step 5: Sum check = 1.000000
The computed values confirm our hand calculation. Notice how dramatically the temperature has concentrated probability on "beautiful": it captures over 81% of the probability mass despite its logit being only 1.5 units above the second-highest token. The exponential nature of softmax magnifies even moderate logit differences into large probability gaps.
Implementing Temperature-Controlled Sampling
Let's build a complete temperature sampling implementation. We will start with a function that samples from temperature-scaled logits, then extend it to generate token sequences. The implementation is straightforward because temperature scaling is a single line of code: dividing the logits by before passing them to softmax.
Understanding the implementation details matters because they affect numerical stability. Very low temperatures can cause logits to become very large after scaling, potentially causing floating point overflow before exponentiation. Very high temperatures with very negative logits can cause the softmax denominator to approach zero. Professional implementations use the log-sum-exp trick to handle these edge cases, but for temperatures in the practical range (0.1 to 2.0), the naive implementation works well.
The log-sum-exp trick exploits the fact that for any constant . Choosing ensures all exponentiated values are between 0 and 1, preventing overflow. PyTorch's F.softmax applies this trick internally, so the naive division followed by softmax is numerically safe in practice.
def sample_with_temperature(
logits: torch.Tensor, temperature: float = 1.0
) -> int:
"""Sample a token index from logits with temperature scaling.
Args:
logits: Raw model output scores, shape (vocab_size,)
temperature: Scaling parameter. 1.0 = unchanged, <1 = sharper, >1 = flatter
Returns:
Sampled token index
"""
if temperature <= 0:
# Greedy selection for T <= 0
return logits.argmax().item()
# Apply temperature scaling
scaled_logits = logits / temperature
probs = F.softmax(scaled_logits, dim=0)
# Sample from the distribution
return torch.multinomial(probs, num_samples=1).item()The function handles the edge case of by returning the argmax (greedy decoding). For positive temperatures, it scales logits, converts to probabilities, and samples using PyTorch's multinomial function. The torch.multinomial function performs a single draw from a categorical distribution defined by the probability vector, which is exactly what we want.
# Demonstrate sampling behavior at different temperatures
def sample_distribution(
logits: torch.Tensor, temp: float, n_samples: int = 1000
) -> dict:
"""Sample many times and return frequency distribution."""
counts = {}
for _ in range(n_samples):
idx = sample_with_temperature(logits, temp)
counts[idx] = counts.get(idx, 0) + 1
return {k: v / n_samples for k, v in counts.items()}Empirical sampling frequencies (1000 samples each): Token T=0.5 T=1.0 T=2.0 -------------------------------------------- sunny 0.518 0.290 0.179 cloudy 0.209 0.184 0.163 rainy 0.056 0.092 0.119 nice 0.045 0.092 0.089 terrible 0.004 0.018 0.046 cold 0.016 0.059 0.078 warm 0.033 0.085 0.092 hot 0.014 0.041 0.068 perfect 0.101 0.127 0.129 unpredictable 0.004 0.012 0.037
The empirical frequencies closely match the theoretical probabilities computed earlier. At , samples cluster heavily on "sunny" and "cloudy." At , we see meaningful representation from lower-probability tokens like "warm," "nice," and "cold." This alignment between theoretical probabilities and empirical frequencies is expected: with 1,000 samples, the law of large numbers ensures the empirical distribution converges close to the theoretical one.
Batch Sampling for Efficiency
In practice, we often want to generate multiple completions or compare outputs across temperatures. Looping over a single-sample function is inefficient because it makes many small GPU operations instead of one large one. Here is a vectorized implementation that generates all samples in a single call to torch.multinomial:
def batch_sample_with_temperature(
logits: torch.Tensor, temperature: float = 1.0, num_samples: int = 1
) -> torch.Tensor:
"""Sample multiple tokens efficiently.
Args:
logits: Raw scores, shape (vocab_size,) or (batch, vocab_size)
temperature: Scaling parameter
num_samples: Number of samples to draw
Returns:
Tensor of sampled indices
"""
if temperature <= 0:
if logits.dim() == 1:
return logits.argmax().unsqueeze(0).expand(num_samples)
return logits.argmax(dim=-1).unsqueeze(-1).expand(-1, num_samples)
scaled = logits / temperature
probs = F.softmax(scaled, dim=-1)
if logits.dim() == 1:
return torch.multinomial(
probs, num_samples=num_samples, replacement=True
)
return torch.multinomial(probs, num_samples=num_samples, replacement=True)5 samples at each temperature: T = 0.3: rainy, sunny, sunny, sunny, rainy T = 1.0: sunny, warm, cloudy, hot, perfect T = 2.0: perfect, cloudy, rainy, sunny, warm
At low temperature, we see repeated "sunny" selections. Higher temperatures introduce variety, sometimes surfacing less expected but still contextually reasonable tokens. The batch implementation is much more efficient because torch.multinomial with replacement=True draws all samples in a single vectorized operation rather than looping.
Temperature Selection Guidelines
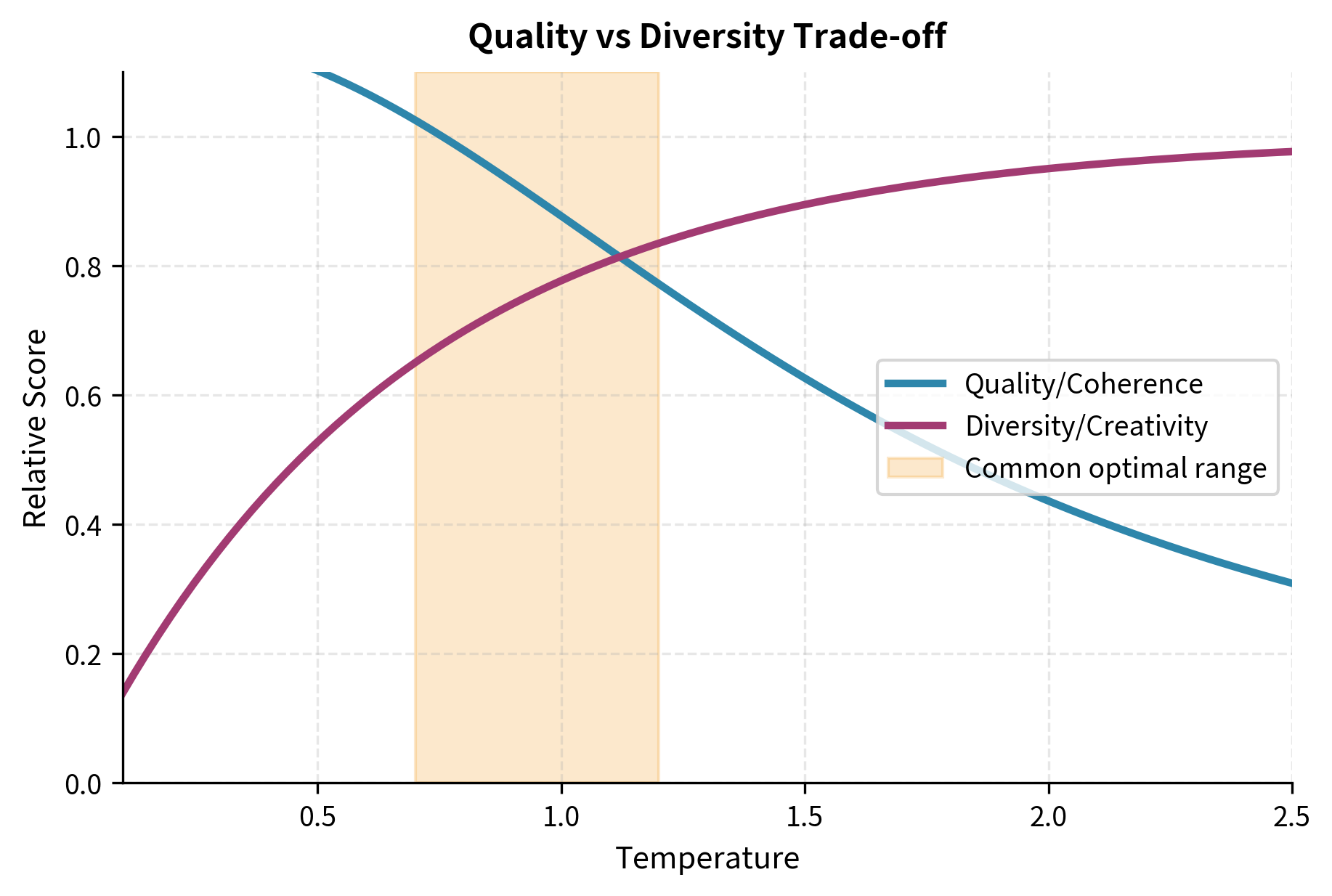
Choosing the right temperature depends on your application. The key insight is that temperature controls the trade-off between coherence and creativity. Lower temperatures produce safer, more predictable text by sharpening the model's probability distribution around its most confident predictions. Higher temperatures introduce novelty by flattening the distribution and giving less probable tokens meaningful chances of being selected. Neither extreme is universally correct: the right setting depends entirely on what you want from the generation.
A useful mental model: think of temperature as adjusting how conservative or adventurous the model's token choices are, not as adding external noise. The model's learned representations are encoded in the logits; temperature only adjusts how boldly the model acts on its preferences. Low temperature means "trust your top choices absolutely." High temperature means "consider your alternatives more seriously."
One practical heuristic: start with as a general-purpose default, which most practitioners find provides a good balance of quality and variety. Then adjust upward if outputs feel repetitive or templated, and adjust downward if outputs feel incoherent or off-topic. Small adjustments of 0.1 to 0.2 units can have significant perceptible effects, so tune incrementally.
Task-Based Recommendations
Different generation tasks call for different temperature settings. This reflects the varying priorities of accuracy versus creativity in each domain. The right temperature for code generation is very different from the right temperature for poetry, because the definition of "good output" differs substantially across tasks.
For tasks where correctness is binary (the code either runs or it does not, the fact is either right or wrong), temperature near zero is almost always preferable. Every step away from the most probable token is a risk of introducing an error. For tasks where quality is subjective and diversity is valuable (creative writing, brainstorming, generating multiple options to choose from), higher temperatures enable the model to produce a broader range of plausible completions. The table below summarizes common task-temperature pairings:
| Task | Recommended T | Rationale |
|---|---|---|
| Code generation | 0.0 - 0.3 | Correctness matters; creativity can introduce bugs |
| Factual Q&A | 0.0 - 0.5 | Accuracy over variety; want the most likely correct answer |
| Translation | 0.3 - 0.7 | Balance fluency with fidelity to source meaning |
| Creative writing | 0.7 - 1.2 | Encourage unexpected but coherent word choices |
| Brainstorming | 1.0 - 1.5 | Explore diverse ideas; some randomness is beneficial |
| Poetry/experimental | 1.2 - 2.0 | Prioritize novelty and surprise |
For code and factual tasks, you often want temperature near zero. A slight temperature (0.1 to 0.2) can prevent the model from getting stuck in repetitive loops while still strongly favoring high-probability outputs. At (pure greedy decoding), the model can get trapped generating the same phrase indefinitely if the context makes that phrase highly probable. A small temperature provides enough stochasticity to escape these loops without much loss in output quality. For creative tasks, temperatures between 0.7 and 1.2 typically produce the best balance of quality and variety, where the model feels expressive rather than robotic without creating nonsensical text.
The Quality-Diversity Trade-off
Temperature creates an inherent trade-off between output quality and output diversity. As you increase temperature, you gain:
- Lexical diversity: More varied word choices, less repetition of the same phrases
- Idea exploration: Access to less probable but potentially interesting continuations
- Reduced mode collapse: Less tendency to repeat the same high-probability phrases and structures
But you also risk:
- Coherence degradation: Sentences that do not follow logically from the preceding context
- Factual errors: Lower-probability (and potentially wrong) claims and statements
- Grammatical mistakes: Unusual token sequences that violate syntactic constraints the model learned
The sweet spot depends on how much you value diversity versus correctness. For a customer service chatbot, coherence and accuracy dominate: use low temperature. For a creative writing assistant, moderate temperature encourages the unexpected turns that make prose interesting. For a coding assistant, deterministic output is almost always preferable: bugs introduced by high-temperature sampling are much more costly than style variation.
The conceptual curves illustrate why practitioners often settle on the 0.7 to 1.2 range. Below 0.7, quality is high but diversity is low: outputs feel correct but robotic, using the same phrases repeatedly. Above 1.2, diversity continues to increase but quality degrades: grammatical errors and factual slips become more common. The optimal zone represents a region where both curves are at acceptable levels. Note that this is a conceptual illustration; the exact curves depend on the model, the task, and how "quality" and "diversity" are defined.
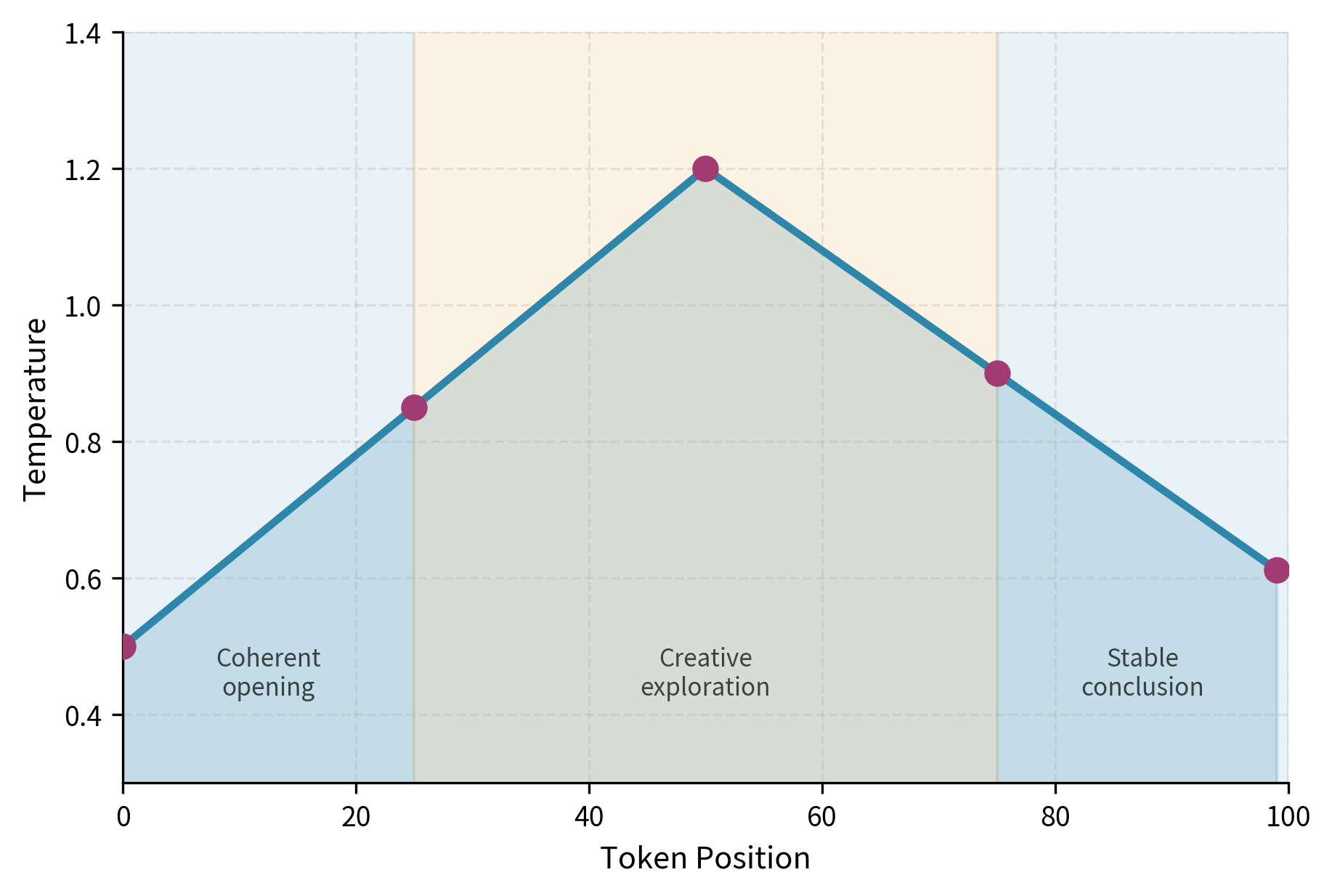
Dynamic Temperature
Some applications benefit from varying temperature during generation. You might start with low temperature to establish a coherent beginning, then increase temperature to introduce variation, then decrease again to conclude coherently. This technique requires careful tuning but can produce text that is both well-structured and creatively varied.
Dynamic temperature is particularly useful for long-form generation tasks like story writing. The opening sentences of a story usually need to be coherent and establish setting and character. The middle can experiment more freely. The conclusion benefits from returning to confident, direct language. By scheduling temperature to match these phases, you can produce output that feels purposeful throughout rather than uniformly cautious or uniformly random.
def dynamic_temperature(
position: int,
total_length: int,
t_start: float = 0.5,
t_peak: float = 1.2,
t_end: float = 0.6,
) -> float:
"""Compute temperature that varies across generation.
Uses a simple curve: starts low, peaks in the middle,
then decreases toward the end.
"""
# Normalized position [0, 1]
p = position / total_length
# Parabolic curve peaking at p=0.5
if p < 0.5:
# Rise from t_start to t_peak
return t_start + (t_peak - t_start) * (2 * p)
else:
# Fall from t_peak to t_end
return t_peak - (t_peak - t_end) * (2 * (p - 0.5))Dynamic temperature across 100-token generation: Position 0 (start): T = 0.50 Position 25: T = 0.85 Position 50 (middle): T = 1.20 Position 75: T = 0.90 Position 99 (end): T = 0.61
Text Generation with a Real Model
Let's put temperature into practice with a complete text generation example using GPT-2. This demonstrates how temperature affects actual model output, not just abstract probability distributions. The key difference from our toy examples is that a real model generates tokens autoregressively: each sampled token is appended to the context, and the model predicts the next token conditioned on everything that came before. Temperature errors accumulate: an unexpected token early in generation can push the model into a context it was not trained on, leading to compounding degradation.
The autoregressive nature of generation also means that temperature has a cascading effect. When you select a less-probable token at position 5, you change the context for all subsequent positions. The model's logits at position 6 are now conditioned on that unusual choice, and those logits may themselves be unusual (because position 6 rarely followed that unusual token in training data). Over many steps at high temperature, this cascading can produce text that drifts far from coherent human language patterns. This is why the "error accumulation" concern is so important for long sequences.
from transformers import GPT2LMHeadModel, GPT2Tokenizer
# Load model and tokenizer
model_name = "gpt2"
tokenizer = GPT2Tokenizer.from_pretrained(model_name)
model = GPT2LMHeadModel.from_pretrained(model_name, _fast_init=False)
model.eval()
# Set pad token to eos token (GPT-2 doesn't have a pad token by default)
tokenizer.pad_token = tokenizer.eos_tokendef generate_with_temperature(
prompt: str,
temperature: float,
max_new_tokens: int = 30,
model=model,
tokenizer=tokenizer,
) -> str:
"""Generate text completion with specified temperature using manual decoding."""
input_ids = tokenizer.encode(prompt, return_tensors="pt")
generated = input_ids.clone()
with torch.no_grad():
for _ in range(max_new_tokens):
outputs = model(generated)
next_token_logits = outputs.logits[:, -1, :]
if temperature <= 0:
# Greedy decoding
next_token = next_token_logits.argmax(dim=-1, keepdim=True)
else:
# Temperature sampling
scaled_logits = next_token_logits / temperature
probs = F.softmax(scaled_logits, dim=-1)
next_token = torch.multinomial(probs, num_samples=1)
generated = torch.cat([generated, next_token], dim=-1)
# Stop at EOS token
if next_token.item() == tokenizer.eos_token_id:
break
return tokenizer.decode(generated[0], skip_special_tokens=True)The generation loop mirrors exactly what we computed in the worked example above, but now operating on GPT-2's full 50,257-token vocabulary at each step. The model processes all generated tokens as context (including the newly added ones) on each iteration, which is why this is called autoregressive generation. Let's generate completions for a prompt at different temperatures:
Prompt: "The future of artificial intelligence is" ============================================================ Temperature = 0.3: ----------------------------------------
in the hands of the next generation of AI. The future of Temperature = 0.7: ----------------------------------------
uncertain, but there's much to like about the prospects. Explore Temperature = 1.0: ----------------------------------------
nowhere near as ambitious. Technological advances have few big promises. So the Temperature = 1.5: ----------------------------------------
world-changing how we all think—take foregone Great Fusion operators Heaven
At , the model produces focused, predictable continuations that sound like confident editorial statements. At , we see more varied vocabulary while maintaining coherence. At , creativity increases but the text may occasionally take unexpected turns in theme or word choice.
Comparing Multiple Samples
One sample does not reveal the full picture. A single draw at might happen to produce a diverse output, and a single draw at might happen to be conservative. The distribution of outputs across many draws is what temperature controls. Let's generate multiple completions at each temperature to see the range of outputs:
def generate_multiple(
prompt: str,
temperature: float,
n_samples: int = 5,
max_new_tokens: int = 20,
) -> list[str]:
"""Generate multiple completions to observe variety."""
completions = []
for _ in range(n_samples):
text = generate_with_temperature(prompt, temperature, max_new_tokens)
# Extract just the generated portion
generated = text[len(prompt) :].strip()
completions.append(generated)
return completionsPrompt: "In a world where robots" Temperature = 0.5: --------------------------------------------------
1. are ubiquitous and the Internet has grown exponentially, it 2. are becoming more and more ubiquitous, it's hard Temperature = 1.0: --------------------------------------------------
1. hunt everything in and at other times, they can 2. abound, one interesting trait that no One has now
At , the samples likely share similar themes and phrasing. At , you will observe more divergent narratives and word choices. This reflects the core promise of temperature: the same prompt can produce different completions depending on how much freedom you give the model to explore.
Measuring Output Diversity
We can quantify diversity by measuring how different the generated samples are from each other. One simple metric is the number of unique n-grams across samples. An n-gram is a sequence of consecutive words; unique n-grams across multiple samples indicate that the model is creating lexically diverse output rather than repeating the same phrases:
def measure_diversity(samples: list[str], n: int = 2) -> dict:
"""Measure n-gram diversity across samples."""
all_ngrams = []
for sample in samples:
words = sample.lower().split()
ngrams = [tuple(words[i : i + n]) for i in range(len(words) - n + 1)]
all_ngrams.extend(ngrams)
total = len(all_ngrams)
unique = len(set(all_ngrams))
return {
"total_ngrams": total,
"unique_ngrams": unique,
"diversity_ratio": unique / total if total > 0 else 0,
}Diversity comparison (10 samples, bigrams): Temperature Total Unique Diversity ------------------------------------------
0.3 27 24 0.889
0.7 21 21 1.000
1.0 20 20 1.000
1.5 23 23 1.000
Higher temperatures produce higher diversity ratios, confirming that the outputs explore a broader range of vocabulary and phrases. The diversity ratio measures what fraction of all n-grams across the samples are unique: a ratio of 1.0 would mean every bigram appeared exactly once (maximum diversity), while a ratio near 0 would indicate that all samples were nearly identical.
Limitations and Impact
Temperature is powerful but imperfect. It is one of the oldest and most universally used generation controls, and it shapes the user experience of virtually every language model deployment. Understanding its limitations helps you know when to rely on it and when to supplement it with other techniques.
The most basic limitation of temperature is that it is a single scalar applied uniformly to all logits. This uniformity means temperature cannot make fine-grained distinctions within the vocabulary. Consider a medical question-answering system where you want diverse phrasing (how the answer is expressed) but not diverse facts (what claims are made). Temperature cannot distinguish between these: raising temperature increases variety in both phrasing and factual content simultaneously. A higher temperature that produces pleasantly varied sentence structures will equally raise the probability of factually incorrect medical claims. This creates a real tension in high-stakes domains where accuracy matters but repetitive outputs frustrate users.
This uniformity limitation also manifests in vocabulary-level problems. Some token types are sensitive to temperature in beneficial ways, like lexical variation in adjectives and adverbs, while others are sensitive in harmful ways, like proper nouns and factual entities. When you generate "The capital of France is," you want temperature to vary how the information is phrased (perhaps "Paris, the City of Light" vs. "Paris, the French capital"), but not to introduce uncertainty about which city is the capital. Temperature applies the same scaling to the logit for "Paris" and the logit for "Lyon," so any temperature above zero gives "Lyon" a non-zero chance of being selected. In practice, models usually have large enough logit gaps for factual entities that low-to-moderate temperatures do not introduce errors, but this provides no formal guarantee.
Temperature also interacts poorly with very long generation. Early tokens sampled at high temperature can push the model into unfamiliar territory, leading to compounding errors as generation proceeds. A single unusual word choice in token 5 might make token 50 completely incoherent, because the model's probability distributions are conditioned on everything that came before. The model was trained on coherent text and may produce high-quality continuations of any coherent prefix, but if temperature sampling introduces an incoherent prefix early on, the model has no mechanism to "recover" and get back on track. This is why many practitioners combine temperature with other techniques like top-k or nucleus sampling, covered in the following chapters, which constrain the damage from high-temperature sampling by preventing the model from assigning meaningful probability to the most implausible tokens.
Temperature can also interact unexpectedly with certain training techniques. Models trained with reinforcement learning from human feedback (RLHF) sometimes have sharpened distributions on "safe" responses and flattened distributions on "unsafe" responses. Raising temperature on such a model may disproportionately increase the probability of off-policy or harmful content, because the RLHF training suppressed those outputs without eliminating them, and temperature can partially resurrect them. Practitioners using RLHF-trained models often combine temperature with system-level safety constraints rather than relying on temperature alone to ensure output quality.
Another subtle limitation: temperature is applied at the individual token level, not at the sequence or sentence level. Even at , the model might produce a sentence that is locally coherent (each token follows from the previous) but globally incoherent (the overall sentence does not make sense). The local nature of autoregressive generation means that temperature controls randomness at each individual step without any mechanism for global coherence checking. Beam search and other sequence-level decoding strategies attempt to address this by considering multiple candidate sequences simultaneously, but temperature applies to single-step sampling.
Despite these limitations, temperature fundamentally shaped how we interact with language models. Before temperature scaling became standard, language model outputs felt robotic and predictable. Temperature gave users a dial to explore the space of possible outputs, making language models feel more creative and less deterministic. The concept transfers beyond language: temperature-like parameters appear in image generation (diffusion model guidance scales), music synthesis, and other generative AI systems. The intuition that "higher temperature means more randomness" has become part of the basic vocabulary of generative AI, understood by practitioners across all modalities.
The success of temperature scaling also revealed something important about language model training. The fact that simply rescaling logits produces coherent but varied outputs suggests that models learn meaningful probability distributions over vocabulary. The relative ordering of token probabilities carries semantic information: "sunny" really is more appropriate than "elephant" after "The weather today is," and temperature preserves this ordering while adjusting the degree of concentration. A model with poorly calibrated logits (where the numerical values do not reflect true relative likelihoods) would produce bizarre behavior when temperature is adjusted, suggesting that large language models learn to assign logit values that are informative about the appropriateness of continuations.
Summary
Temperature controls the sharpness of the probability distribution during language model sampling. By dividing logits by a temperature parameter before softmax, we can make the distribution more peaked (low ) or more uniform (high ). The mechanism is mathematically clean: temperature amplifies or compresses logit differences, which exponentiates into multiplicative changes in probability ratios.
Key takeaways:
- preserves the learned distribution. Lower values sharpen it; higher values flatten it.
- approaches greedy decoding (argmax). approaches uniform random sampling.
- Practical ranges typically fall between 0.1 and 2.0, with most applications using 0.3 to 1.2.
- Task matters: Factual and code generation prefer low temperature. Creative writing benefits from higher values.
- Temperature controls the quality-diversity trade-off: more diversity comes at the cost of coherence.
- Temperature affects all tokens uniformly, which can be limiting when you want selective diversity.
- The probability ratio between any two tokens is , so temperature acts by rescaling the effective logit gap between all pairs of tokens.
- Entropy of the output distribution increases monotonically with temperature. This provides a precise measure of how much randomness temperature introduces.
Temperature is often combined with top-k and nucleus (top-p) sampling to get finer control over the output distribution. These techniques, covered in the following chapters, truncate the distribution before sampling, preventing temperature from giving meaningful probability to highly unlikely tokens. The combination of temperature (which controls how peaked the distribution is) and top-p sampling (which cuts off the tail of the distribution) is one of the most effective and widely used generation strategies in practice.
Key Parameters
When implementing temperature-controlled sampling, these parameters determine behavior:
-
temperature(float, typically 0.1-2.0): The scaling factor applied to logits before softmax. Values below 1.0 sharpen the distribution, making high-probability tokens more dominant. Values above 1.0 flatten the distribution, giving lower-probability tokens more chance. A value of 1.0 preserves the original learned distribution. -
do_sample(bool): Whether to sample from the distribution (True) or use greedy decoding (False). Temperature only affects output whendo_sample=True. Withdo_sample=False, the model always selects the highest-probability token regardless of temperature. -
top_k(int, 0 to disable): When combined with temperature, restricts sampling to the top k most probable tokens. Settingtop_k=0disables this constraint, letting temperature to affect the full vocabulary distribution. -
top_p(float, 0.0-1.0): Nucleus sampling threshold, often used alongside temperature. Settingtop_p=1.0disables nucleus sampling, isolating the temperature effect. Lower values restrict sampling to tokens whose cumulative probability reaches the threshold. -
max_new_tokens(int): Maximum number of tokens to generate. Longer sequences at high temperature tend to accumulate errors, so consider lower temperatures for longer outputs.
For most applications, start with temperature=0.7 and adjust based on output quality. Decrease if outputs are too random or incoherent; increase if outputs are too repetitive or predictable.
Quiz
Ready to test your understanding? Take this quick quiz to reinforce what you've learned about decoding temperature and probability distribution control.
Decoding Temperature
Reference
Citation details
Cite or share this article.
Continue with the full handbook
This chapter is part of Language AI Handbook. Use the handbook page to browse the complete table of contents and continue reading in sequence.
Explore Language AI HandbookStay up to date
Get articles, book updates, and news delivered to your inbox.
No spam, unsubscribe anytime.
Join the community
Sign in to remove popups, track your reading progress, and join the discussion.
Comments
No comments yet. Be the first to share your thoughts!