Learn how YaRN extends LLM context length through wavelength-based frequency interpolation and attention temperature correction. Includes mathematical formulation and implementation.

This article is part of the free-to-read Language AI Handbook
YaRN: Yet another RoPE extensioN
Extending context length in large language models has become a central challenge. Models trained on sequences of 2,048 or 4,096 tokens struggle when asked to process documents spanning tens of thousands of positions. Position Interpolation offered one solution: scale down position indices to fit within the trained range. NTK-aware scaling improved upon this by preserving high-frequency components that capture local relationships. But both methods still leave performance on the table, particularly as the extension factor grows large.
YaRN, which stands for "Yet another RoPE extensioN," addresses limitations in both approaches. The key insight is that extending context length doesn't just require fixing position encodings. It also requires compensating for a subtle but significant change in attention score distributions. When we stretch positions across longer sequences, the entropy of attention distributions shifts in ways that degrade model behavior. YaRN tackles this through a combination of targeted frequency interpolation and an attention temperature correction.
This chapter develops YaRN from its motivation through its complete formulation. We'll see why existing methods fall short at large extension factors, derive the attention scaling mechanism, and implement YaRN step by step. By the end, you'll understand how this technique enables models to maintain quality at context lengths 16x or 32x beyond their training distribution.
The Problem with Existing Methods
Before diving into YaRN, let's understand why Position Interpolation and NTK-aware scaling leave room for improvement. Both methods successfully enable RoPE-based models to process longer sequences, but they introduce subtle distortions that accumulate as the extension factor increases.
Position Interpolation works by scaling all position indices by a factor : a position becomes . This keeps all positions within the trained range, but it compresses the entire frequency spectrum uniformly. High-frequency dimensions that previously distinguished positions 1 apart now need to distinguish positions apart after compression. The model loses fine-grained position discrimination.
NTK-aware scaling addresses this by adjusting the base frequency rather than scaling positions directly. This preserves high-frequency components while stretching low-frequency ones. The approach works well for moderate extensions (2x to 4x), but at larger factors, even NTK-aware scaling begins to degrade.
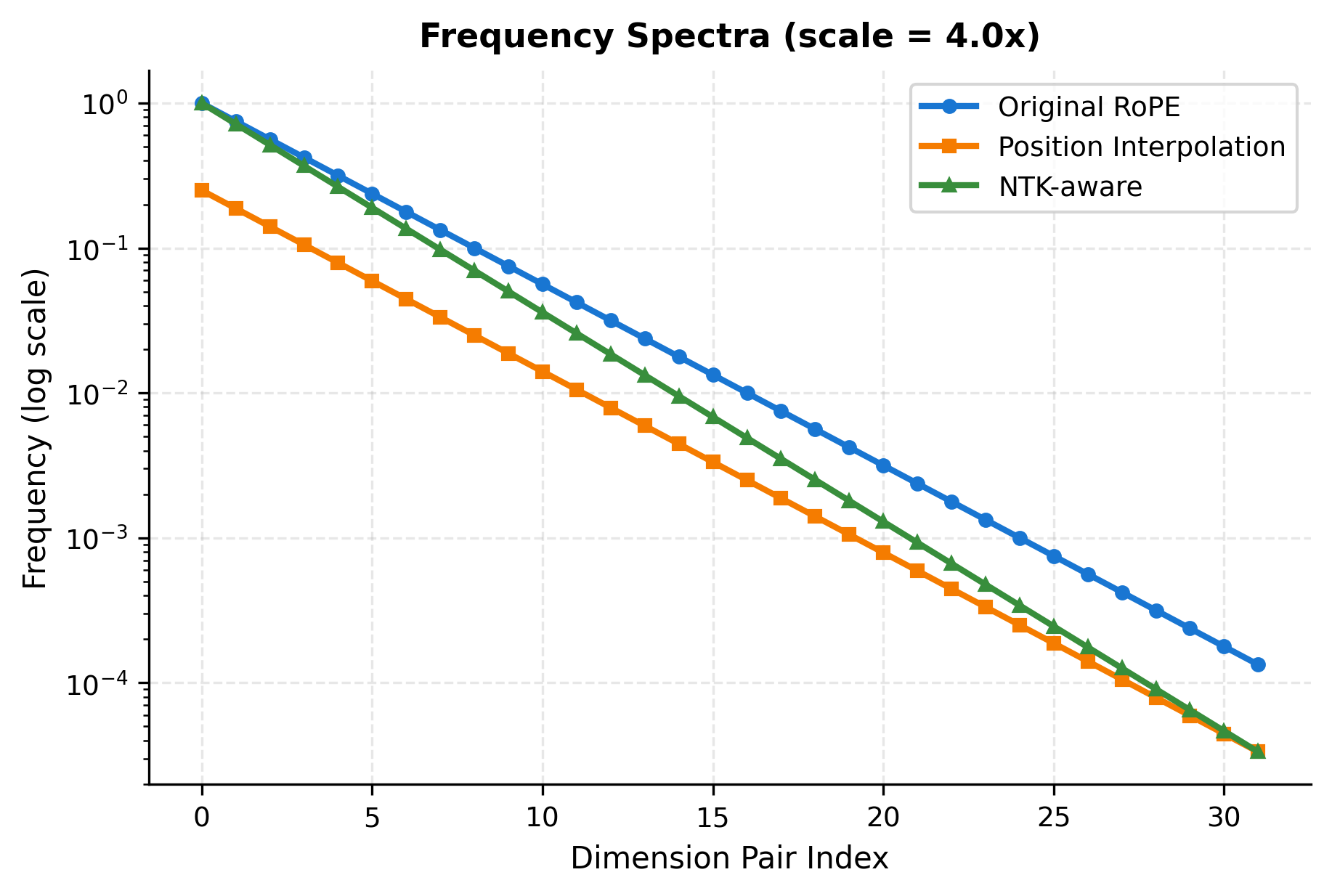
Let's visualize how these methods transform the frequency spectrum:
The visualization reveals a fundamental trade-off. Position Interpolation maintains the relative spacing between frequencies (the lines are parallel on a log scale) but shifts everything down. NTK-aware scaling bends the curve, keeping high frequencies close to original while aggressively stretching low frequencies. Neither approach is optimal across all dimension pairs.
Attention Entropy and the Temperature Problem
Beyond frequency adjustments, there's a more subtle issue that neither PI nor NTK-aware scaling addresses: attention entropy shifts. When we modify RoPE frequencies, we change the distribution of attention scores in ways that affect model behavior.
Recall that attention scores are computed as the scaled dot product between query and key vectors:
where:
- : the attention score between a query at position and a key at position
- : the RoPE-rotated query vector at sequence position
- : the RoPE-rotated key vector at sequence position
- : the dimension of the key vectors, used for scaling to prevent dot products from growing too large
- : the dot product between query and key, measuring their similarity
When we interpolate positions, the effective distances between tokens change. Positions that were far apart now appear closer in the rotated space. This compresses the range of attention scores, making them more uniform. Higher uniformity means higher entropy: the model attends more diffusely rather than focusing on specific positions.
The entropy of an attention distribution measures how spread out the attention weights are. Low entropy means the model focuses sharply on a few positions. High entropy means attention is distributed more evenly across many positions. Changes to position encoding can inadvertently shift this entropy, degrading the model's ability to focus.
Let's quantify this effect by computing attention entropy under different interpolation schemes:
The entropy values reveal the effect of position interpolation on attention patterns. While the differences might seem small in absolute terms, they compound across layers and affect the model's ability to retrieve and aggregate information from specific positions. YaRN addresses this by introducing an attention temperature correction.
The YaRN Solution
YaRN combines two complementary mechanisms to enable high-quality context extension:
-
Ramp-based frequency interpolation: Rather than treating all dimension pairs equally (like PI) or smoothly transitioning across all pairs (like NTK), YaRN uses a ramp function that applies no interpolation to high-frequency pairs, full interpolation to low-frequency pairs, and a smooth transition in between.
-
Attention temperature scaling: YaRN introduces a scaling factor to attention scores, where is derived to compensate for the entropy increase caused by interpolation. When (no extension), and no scaling is applied.
The combined approach modifies both the rotation frequencies and the attention computation. For frequencies, YaRN applies a dimension-specific adjustment:
where:
- : the adjusted frequency for dimension pair after YaRN modification
- : the original RoPE frequency for dimension pair , computed as
- : the interpolation factor, a value between and that depends on the wavelength ratio
- : the wavelength-to-context ratio for dimension pair
- : the wavelength for dimension pair (positions per full rotation)
- : the original training context length
For attention scores, YaRN introduces a temperature correction:
where:
- : the temperature-adjusted attention score
- : the temperature scaling factor, where increases score magnitude
- : the temperature parameter, computed from the extension factor
Let's develop each component in detail.
Wavelength Analysis
To understand why some dimension pairs need interpolation while others don't, we need to think about rotation in terms of wavelength rather than frequency. While frequency tells us how fast something rotates (radians per position), wavelength tells us how far we must travel for one complete cycle (positions per full rotation). Wavelength provides a more intuitive picture because we can directly compare it to the context length.
Think of it this way: if a dimension pair completes 100 full rotations during the training context, it has learned to use those rotations to distinguish positions at a fine-grained level. Extending the context by 4x means it now completes 400 rotations. No problem. The pair can still distinguish positions just as well as before. But if a dimension pair completes only 0.1 rotations during training (barely moving at all), extending by 4x means it now needs to cover 0.4 rotations. That's still not a complete cycle, and the model has never seen rotation patterns beyond what it learned during training.
The wavelength of dimension pair is the inverse of the frequency, scaled by :
where:
- : the wavelength (in positions) for dimension pair , representing how many sequence positions correspond to one complete rotation
- : the base frequency for dimension pair , measured in radians per position
- : the total embedding dimension (must be even)
- : the dimension pair index (0, 1, ..., )
- : the number of radians in a complete rotation (one full cycle)
- : the RoPE base constant, which controls the frequency range
The second equality follows by substituting the definition of and simplifying: .
The critical question becomes: how does each wavelength compare to the training context length ? If , the pair completes at least one full rotation during training, meaning the model has seen all possible rotation states. If , the pair completes less than one rotation, meaning the model has only seen a fraction of the rotation cycle. This ratio will be central to YaRN's design.
The "vs Original L" column shows the wavelength ratio . This ratio is the key to understanding which dimension pairs need interpolation:
- When , the wavelength is shorter than the context, meaning the pair completes multiple full rotations during training. These pairs have learned the full rotation cycle.
- When , the wavelength exceeds the context, meaning the pair doesn't complete even one rotation during training. These pairs operate in a limited portion of the rotation cycle.
Let's trace through the table to build intuition. Dimension pair 0 has a wavelength of about 6 positions and . It completes roughly 340 full rotations within the training context, so it has thoroughly learned how to use rotation for position encoding. When we extend to 8,192 positions, pair 0 still completes over 1,300 rotations. No problem here.
At the other extreme, dimension pair 31 has a wavelength of around 60,000 positions and . During training, it completes only about 3% of a single rotation. The model has learned to encode position using just this small arc of the rotation cycle. If we extend the context by 4x without interpolation, we'd ask pair 31 to cover 12% of its rotation cycle, using rotation states it has never encountered. This is extrapolation, and it degrades model quality.
The pattern is clear: pairs with small don't need interpolation; pairs with large do. The question is where to draw the line, and whether the transition should be abrupt or smooth. YaRN's ramp function provides the answer.
The YaRN Ramp Function
Now we can design a function that decides how much interpolation each dimension pair receives. We want three behaviors:
- For pairs with small (short wavelengths, many rotations during training): apply no interpolation, leaving them at their original frequencies.
- For pairs with large (long wavelengths, few rotations during training): apply full interpolation, scaling them by just like Position Interpolation would.
- For pairs with intermediate : apply partial interpolation, blending smoothly between the two extremes.
This is exactly what a ramp function achieves. YaRN defines as a piecewise function:
where:
- : the wavelength-to-context ratio for dimension pair , comparing the rotation period to the training context
- : the wavelength for dimension pair
- : the original training context length (e.g., 2048 or 4096 tokens)
- : the extension scale factor (e.g., 4 for extending from 2048 to 8192)
- : the lower threshold (typically 1.0), below which no interpolation is applied
- : the upper threshold (typically 32.0), above which full interpolation is applied
- : the interpolation weight in the ramp region, ranging from 0 to 1
- : the output interpolation factor, ranging from 1 (no interpolation) to (full interpolation)
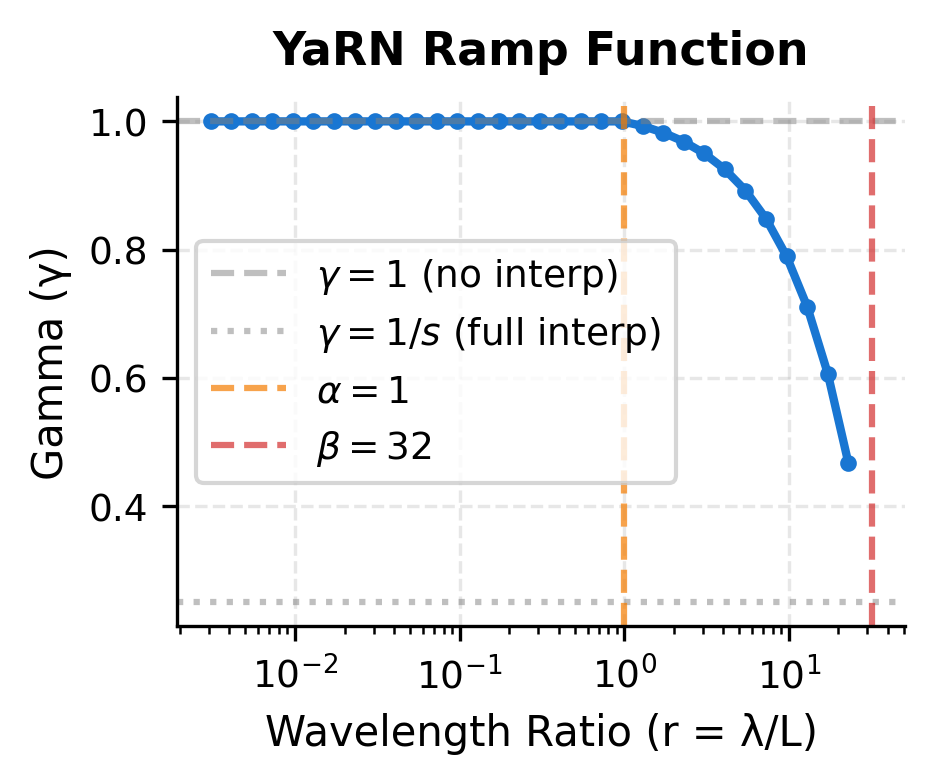
Let's unpack the middle case, which is the most interesting. The weight measures where falls within the transition region . At the left edge (), we have , so the expression becomes . At the right edge (), we have , giving . For values between the edges, we get a linear blend. This creates a smooth ramp rather than an abrupt step, which helps the model adapt more gracefully.
The default thresholds have intuitive interpretations. When , dimension pairs with wavelength less than the context length (completing at least one full rotation during training) don't need interpolation. When , dimension pairs with wavelength more than 32 times the context length (completing less than 3% of a rotation) need full interpolation. These values were empirically validated across multiple model architectures, striking a balance between preserving high-frequency information and ensuring stable extrapolation.
To summarize, the ramp function creates three distinct regions:
-
Short wavelengths (): These pairs already rotate many times within the original context. They don't need interpolation because they can naturally handle the extended positions.
-
Long wavelengths (): These pairs rotate slowly and need full Position Interpolation treatment to avoid extrapolation.
-
Middle wavelengths (): These pairs receive partial interpolation, smoothly blending between the two extremes.
Let's visualize the ramp function and its effect on frequencies:
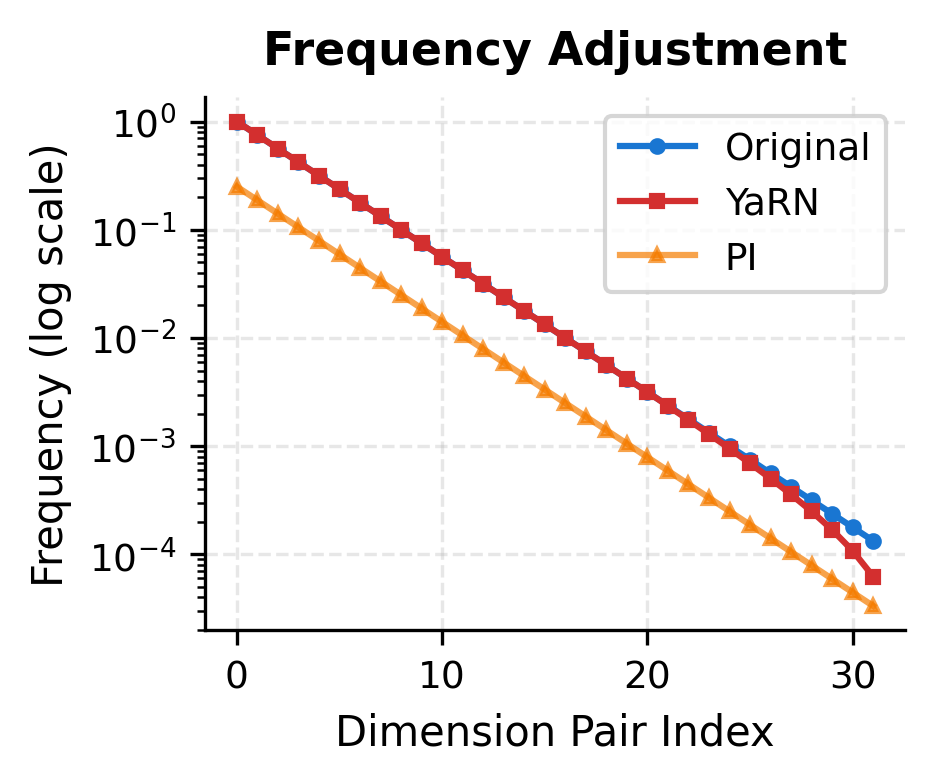
The ramp function creates a piecewise linear transition on the log-wavelength scale. The left panel shows how drops from 1 to as wavelength increases. The right panel shows the resulting frequency spectrum: YaRN preserves high frequencies (matching the original) while smoothly transitioning to interpolated low frequencies.
Attention Temperature Scaling
We've now addressed the frequency problem with the ramp function. But recall that we identified two problems at the start: frequency distortion and entropy shift. Even with perfect frequency adjustments, interpolation changes something fundamental about attention patterns.
To understand why, think about what interpolation does geometrically. When we slow down rotations (by multiplying frequencies by ), positions that were previously "far apart" in the rotated embedding space now appear "closer." Consider two tokens at positions 0 and 100. In the original RoPE, pair 0 might rotate these to be 100 radians apart (after wrapping). With interpolation, the same pair rotates them to only 25 radians apart (for 4x extension). This compression happens across all interpolated dimension pairs.
This compression has a direct consequence for attention scores. The dot product between query and key vectors measures their similarity. When positions appear closer together in the rotated space, the dot products become more similar to each other. The range of attention scores shrinks.
Now recall how softmax works. Given a vector of scores :
When input scores are spread out (high variance), exponentiating amplifies the differences, producing a peaked distribution that focuses on the highest scores. When input scores are compressed (low variance), the exponentials are more similar, producing a flatter, more uniform distribution. This increased uniformity is what we measure as higher entropy.
The solution is conceptually simple: if scores are too compressed, stretch them back out. We do this by multiplying the scores by a factor greater than 1 before applying softmax. In temperature scaling terminology, we reduce the "temperature" (making the distribution sharper) by dividing by a temperature , or equivalently, multiplying by . YaRN frames this as multiplying by where .
The temperature factor is computed as:
where:
- : the attention temperature scaling factor (always )
- : the context extension scale factor (e.g., 4 for 4x extension)
- : the natural logarithm of the extension factor
- : an empirically determined coefficient that controls the rate of temperature increase
- : the base value ensuring when (no extension)
Why rather than directly? This relates to how variance scales under multiplication. If we multiply scores by a constant , the variance of the scores is multiplied by . So to increase variance by a factor of , we need to multiply the scores by .
The logarithmic form of captures an empirical observation: the entropy shift doesn't grow linearly with the extension factor. Larger extensions need progressively less aggressive correction. Doubling the extension factor from 4x to 8x doesn't require doubling the temperature adjustment. Instead, it adds a constant amount: , contributing an additional to .
The column shows the actual multiplier applied to attention scores. Even for very large extension factors (128x), the multiplier stays below 1.2, indicating that temperature correction is a subtle adjustment rather than a dramatic rescaling.
The temperature factor grows slowly with extension factor. For a 4x extension, we multiply attention scores by . For 32x extension, the multiplier is . These modest corrections help maintain attention sharpness.
Let's verify the effect on entropy:
Temperature scaling helps bring the entropy closer to the original distribution. While the match isn't perfect (which is expected given the fundamental changes to the attention geometry), the correction prevents the excessive entropy increase that would otherwise occur.
The Complete YaRN Formula
Now we can put together the complete YaRN transformation. Given a model trained on context length that we want to extend by factor , the process involves three steps.
Step 1: Compute adjusted frequencies
For each dimension pair with base frequency and wavelength , compute the adjusted frequency:
where:
- : the adjusted frequency for dimension pair
- : the original RoPE frequency
- : the ramp function defined earlier
- : the wavelength ratio that determines the interpolation amount
Step 2: Apply RoPE with adjusted frequencies
For query or key vector at position , apply the block-diagonal rotation matrix:
where:
- : the rotated vector, now incorporating YaRN's frequency adjustments
- : a 22 rotation matrix for angle , applied to dimension pair
- : the rotation angle, which increases linearly with position at the adjusted rate
- The block-diagonal structure means each dimension pair is rotated independently
Step 3: Apply temperature scaling to attention scores
After computing the raw attention scores, apply the temperature correction:
where:
- : the scaled attention score between positions and
- : the YaRN-rotated query vector at position
- : the YaRN-rotated key vector at position
- : the dimension of key vectors
- : the temperature factor, computed from the extension scale
- : the scaling multiplier applied to raw scores (increases score magnitude to sharpen attention)
- The scaling occurs before softmax normalization
Let's test the complete YaRN implementation:
The implementation confirms that YaRN preserves vector magnitudes (rotation is an isometry) while applying the adjusted frequencies.
Visualizing YaRN's Effect
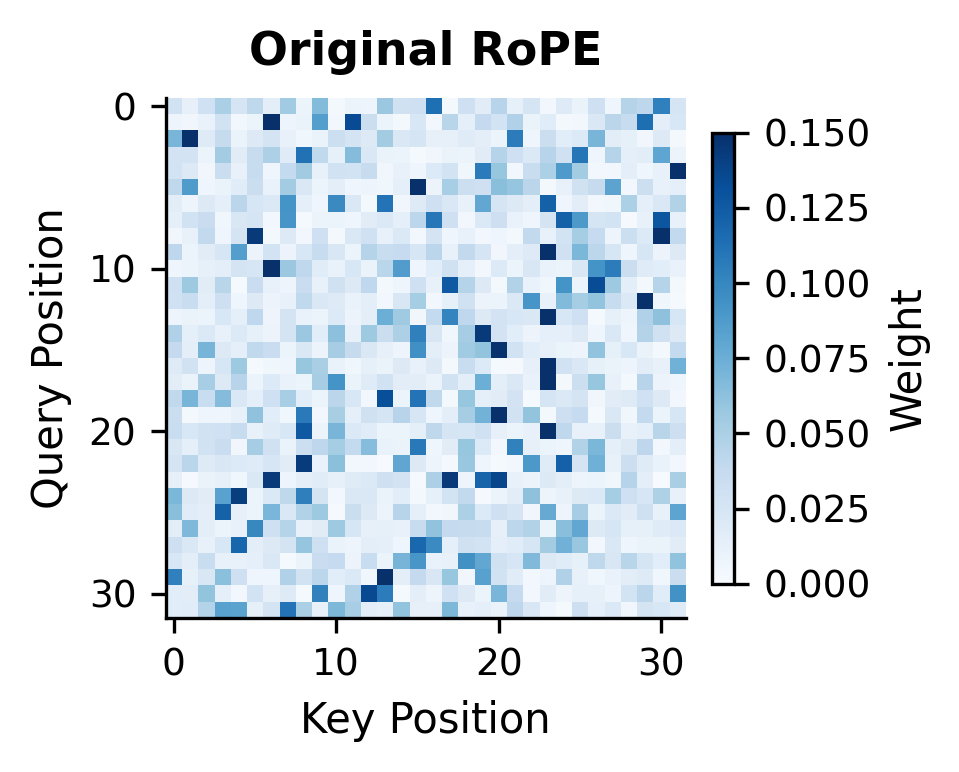
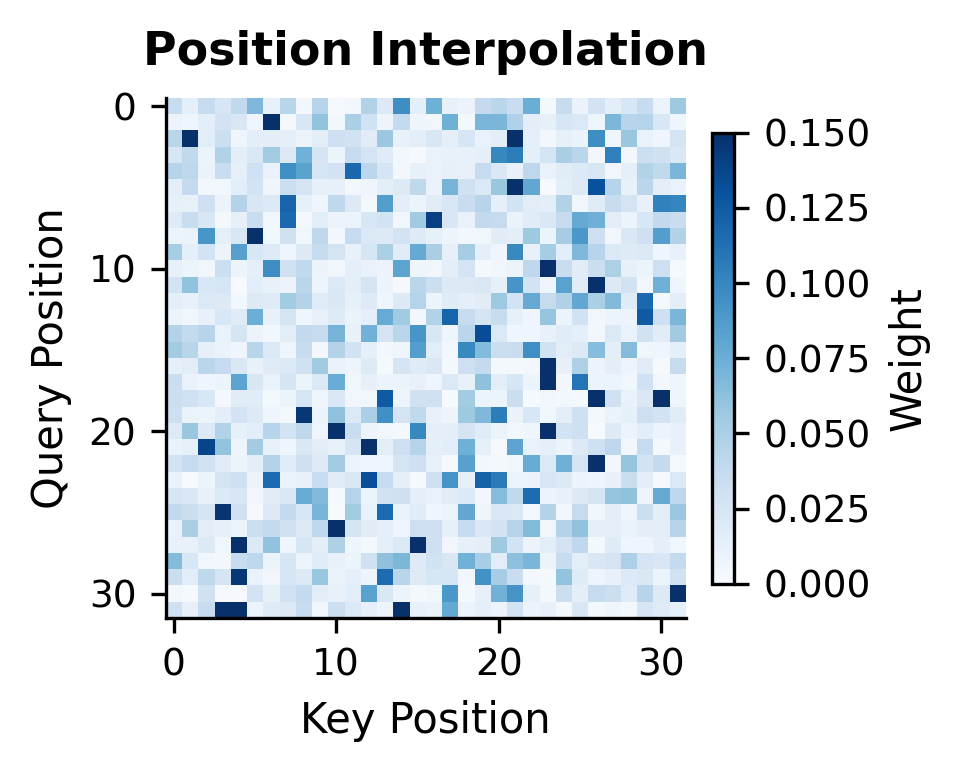
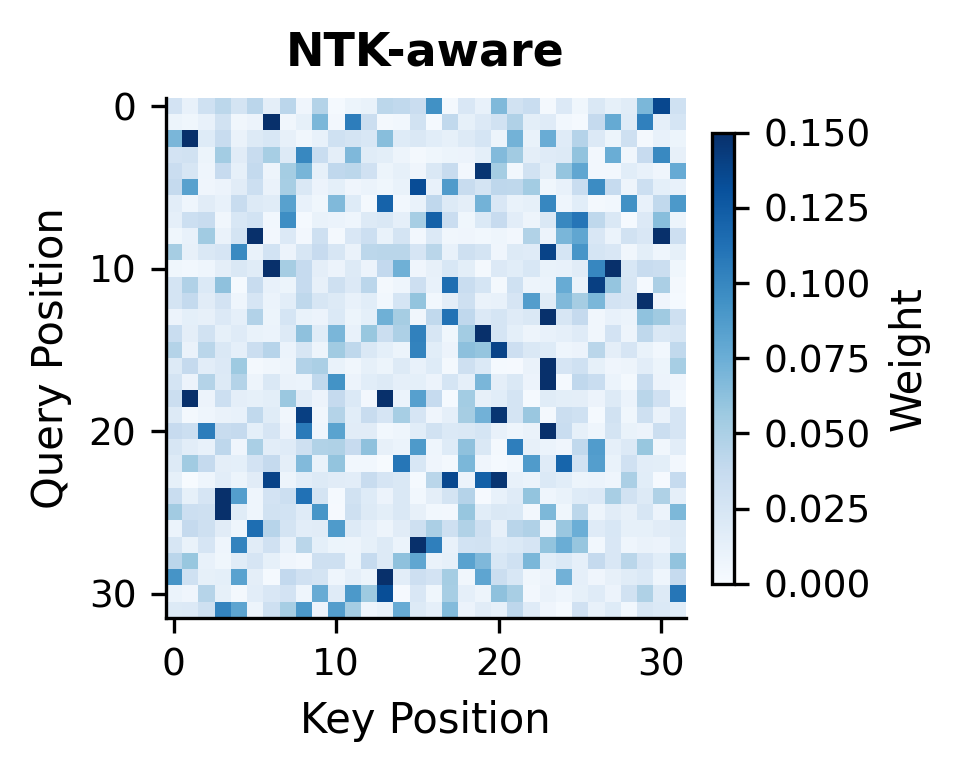
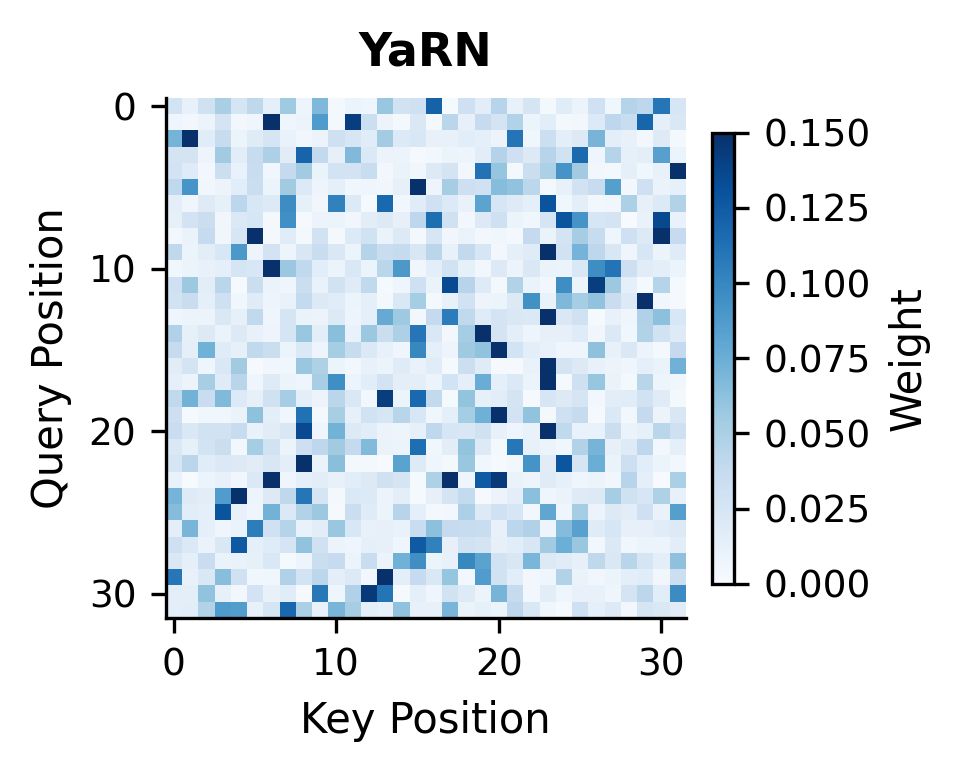
Let's visualize how YaRN affects the attention patterns compared to other methods:
The attention heatmaps reveal the differences between methods. YaRN produces patterns that more closely resemble the original RoPE attention, with sharper focus on relevant positions rather than the diffuse patterns seen with Position Interpolation.
YaRN Training Requirements
An important practical consideration is whether YaRN requires fine-tuning. The answer depends on the extension factor:
For modest extensions (2x to 4x): YaRN can often be applied without any fine-tuning, leveraging the model's existing weights. The frequency adjustments and temperature scaling are designed to minimize the distribution shift.
For larger extensions (8x to 32x): Brief fine-tuning significantly improves quality. The YaRN paper recommends 200 to 400 training steps on long-context data, much less than training from scratch.
For extreme extensions (64x+): Longer fine-tuning becomes necessary, though still much shorter than pre-training from scratch.
The key advantage of YaRN over naive approaches is the efficiency of this fine-tuning. Because the method preserves the essential structure of the position encoding while making targeted adjustments, the model needs to learn only minor adaptations rather than fundamentally new position representations.
YaRN vs Alternatives
Let's summarize how YaRN compares to other context extension methods:
| Method | Key Mechanism | Strengths | Weaknesses |
|---|---|---|---|
| Position Interpolation | Uniform position scaling | Simple, no new parameters | Loses high-frequency information |
| NTK-aware | Base frequency adjustment | Better frequency preservation | Still uniform across dimensions |
| Dynamic NTK | Position-dependent scaling | Adapts to sequence length | Complex, training instability |
| YaRN | Ramp function + temperature | Selective interpolation, entropy control | Two hyperparameters (α, β) |
The main advantages of YaRN are:
-
Selective preservation: High-frequency dimensions that don't need interpolation are left unchanged, maintaining fine-grained position discrimination.
-
Entropy control: Temperature scaling prevents the attention distribution from becoming too diffuse, preserving the model's ability to focus.
-
Efficient adaptation: The targeted adjustments require less fine-tuning to adapt to than more disruptive methods.
-
Predictable behavior: The ramp function provides intuitive control over which dimensions are interpolated and by how much.
The "Mean Entropy" column shows how diffuse the attention distribution is, with lower values indicating sharper focus. The "Rel. Pos. Error" measures whether the same relative distance produces the same attention score at different absolute positions. Values near zero indicate perfect relative position encoding.
The comparison shows that YaRN achieves entropy closer to the original while maintaining the relative position property (low position error). The combination of targeted interpolation and temperature scaling addresses both the frequency and entropy aspects of context extension.
Limitations and Considerations
Despite its effectiveness, YaRN has limitations worth understanding.
Hyperparameter sensitivity: The and parameters control the ramp function's transition region. While the defaults (1 and 32) work well for many models, some architectures may benefit from tuning. Models with different RoPE bases or dimension sizes may require adjustment.
Temperature approximation: The temperature formula is empirically derived rather than theoretically optimal. It works well in practice but may not perfectly compensate for entropy shifts in all scenarios.
Integration complexity: Unlike Position Interpolation (which only modifies position indices) or NTK-aware scaling (which only modifies the base), YaRN requires two separate modifications. Both the frequency adjustment and the attention scaling must be implemented correctly.
Interaction with other optimizations: When combined with techniques like FlashAttention or grouped-query attention, care must be taken to apply the temperature scaling at the correct point in the computation. The scaling should occur before the softmax, not after.
These limitations are manageable in practice. YaRN has been successfully integrated into many open-source models, and the community has developed reference implementations that handle the integration details correctly.
Key Parameters
When implementing YaRN, several parameters control its behavior:
-
scale: The context extension factor (e.g., 4.0 for extending from 2048 to 8192 tokens). Larger values enable longer contexts but may require more fine-tuning. -
alpha: The lower wavelength threshold (default: 1.0). Dimension pairs with wavelength-to-context ratio below this value receive no interpolation. Decreasing applies interpolation to more dimension pairs. -
beta: The upper wavelength threshold (default: 32.0). Dimension pairs with wavelength-to-context ratio above this value receive full interpolation. Increasing delays full interpolation to higher wavelength pairs. -
base: The RoPE frequency base (default: 10000). This should match the base used in the original model's RoPE implementation. -
original_context: The context length the model was originally trained on (e.g., 2048 or 4096). This determines the wavelength ratios used in the ramp function.
For most applications, the default values of and work well. The primary parameter to adjust is scale, which should be set to the desired extension factor. If the model uses a non-standard RoPE base, ensure base matches the original configuration.
Summary
YaRN provides a principled approach to extending context length in RoPE-based language models. By combining selective frequency interpolation with attention temperature scaling, it addresses limitations in both Position Interpolation and NTK-aware methods.
Key takeaways:
-
Wavelength-based interpolation: YaRN uses a ramp function to apply no interpolation to high-frequency dimension pairs, full interpolation to low-frequency pairs, and a smooth transition in between. This preserves fine-grained position information where it matters.
-
Attention temperature correction: Context extension changes attention score distributions, increasing entropy. YaRN compensates with a temperature scaling factor where .
-
Efficient fine-tuning: The targeted adjustments minimize distribution shift, enabling effective context extension with as few as 200 to 400 fine-tuning steps for moderate extension factors.
-
Complementary to other methods: YaRN can be seen as a refinement that combines insights from Position Interpolation (full interpolation for long wavelengths) and NTK-aware scaling (preservation of short wavelengths), while adding the novel temperature correction.
-
Practical deployment: YaRN has been integrated into many open-source models and inference frameworks, demonstrating its practical viability for real-world context extension.
The next chapter explores attention sinks, a phenomenon where transformer models allocate disproportionate attention to initial tokens regardless of their semantic relevance, and how this affects long-context processing.



Comments