Part of Language AI Handbook
Explains how replaced token detection trains language models 4x more efficiently than masked language modeling.
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Article links
Make inline references clickable
Replaced Token Detection
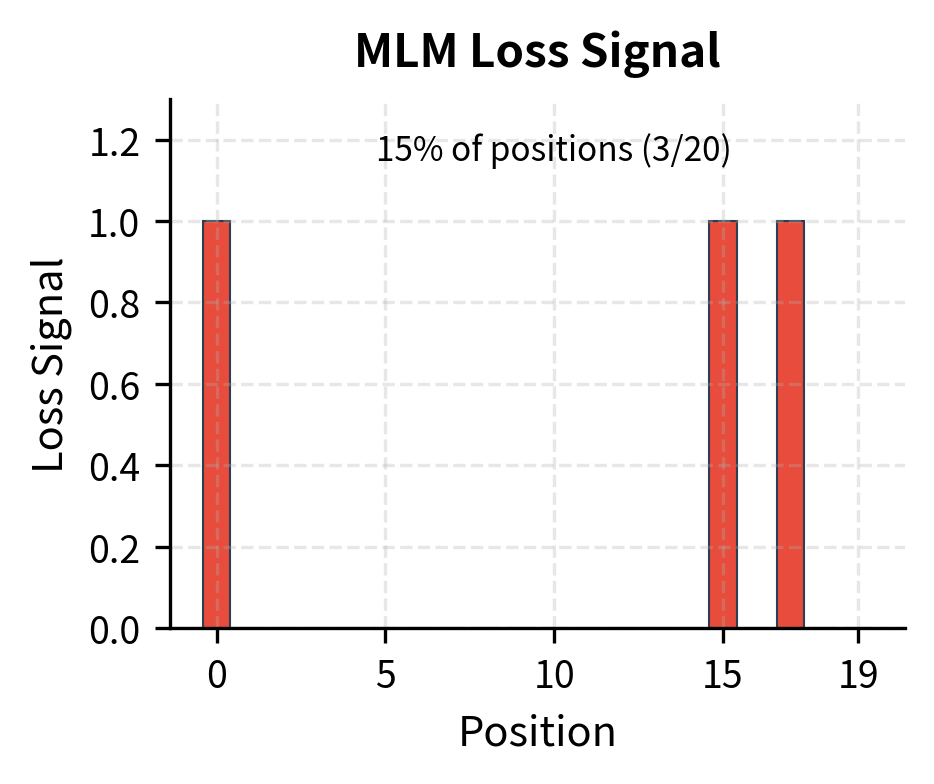
Masked language modeling wastes compute. When BERT masks 15% of tokens and predicts only those positions, 85% of the forward pass produces no training signal. The model processes the entire sequence but learns from a small fraction of it. For expensive pretraining runs consuming millions of GPU hours, this inefficiency is costly. When you multiply that waste across millions of training steps, the cumulative cost in both time and money becomes substantial.
Think of it this way: every time BERT reads a 512-token sequence, it performs a full transformer forward pass over all 512 positions. The attention layers compare every token against every other token. The feed-forward layers transform each position's representation. Yet only about 77 of those positions, the ones that were masked, produce any gradient signal. The other 435 positions are passengers, processed but not learned from. 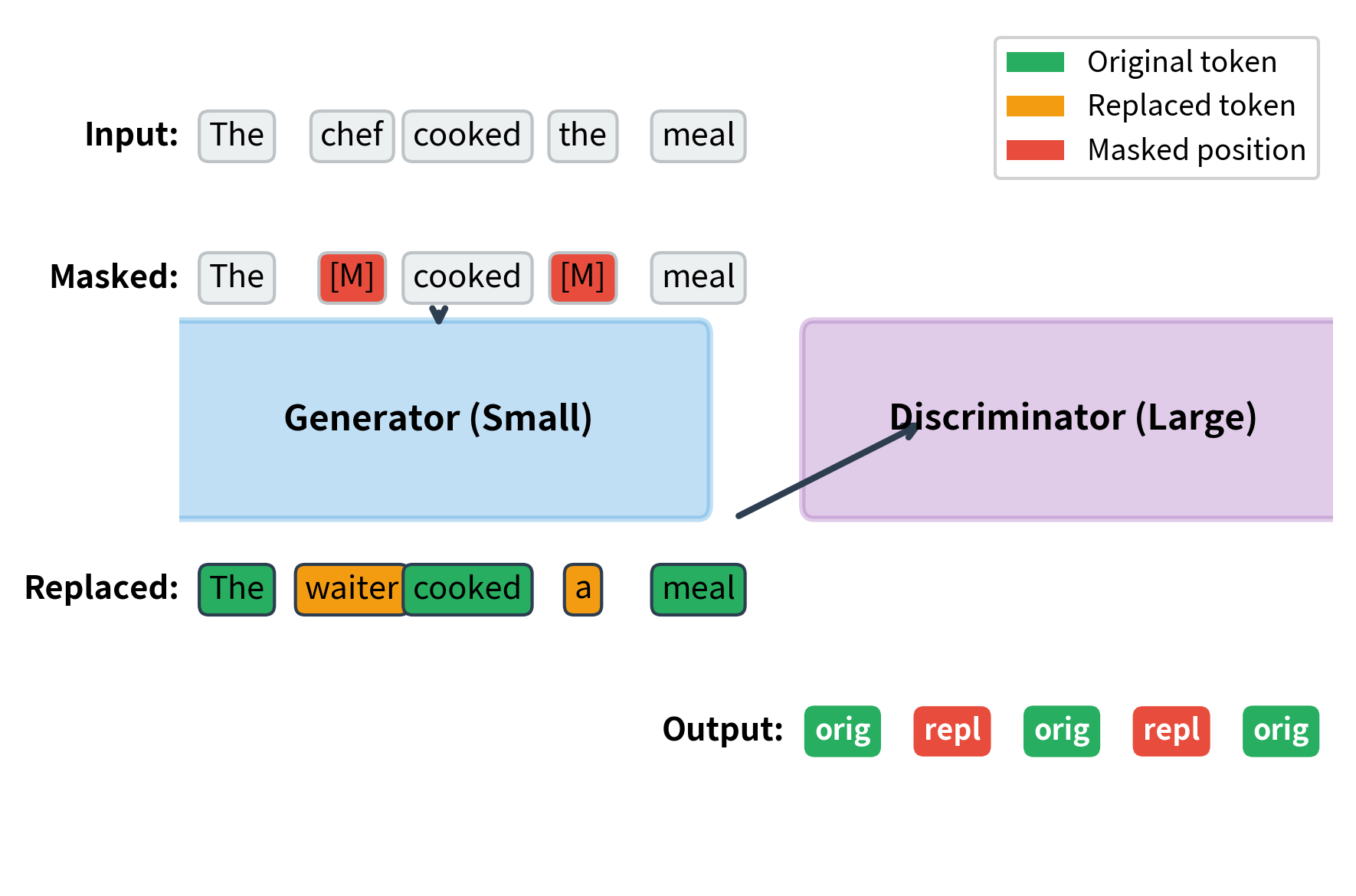This is the inefficiency that Replaced Token Detection (RTD) was designed to eliminate.
Replaced Token Detection solves this problem with a different formulation. Instead of predicting masked tokens, the model classifies every token as either original or replaced. A small "generator" network produces plausible replacements for masked positions, and a larger "discriminator" network learns to detect which tokens have been swapped. Every position contributes to the loss, making training much more sample-efficient. This shift increases how much training signal each sequence provides.
This approach, introduced in the ELECTRA paper in 2020, achieves BERT-level performance with a fraction of the compute. The key insight is that detection is easier than generation: distinguishing real from fake requires less capacity than predicting the exact original token, allowing the model to learn from every position rather than just masked ones. The paper demonstrated that with roughly one-quarter of BERT's pretraining budget, ELECTRA could match or exceed BERT's performance on the GLUE benchmark. This result sent a clear signal to the NLP community: the MLM paradigm, despite its success, had not found the most efficient path to strong representations.
BERT's introduction in 2018 established masked language modeling as the dominant pretraining paradigm, but it also set a worrying precedent: competitive pretraining required enormous compute. Google's BERT-Large required 4 days on 64 TPU chips. The subsequent GPT and RoBERTa models pushed these requirements even higher. By 2019, researchers were asking whether the MLM objective itself was the bottleneck. Kevin Clark and colleagues at Stanford and Google Brain answered this question with ELECTRA (Efficiently Learning an Encoder that Classifies Token Replacements Accurately), published at ICLR 2020. Their central observation, that the 15% masking rate in MLM is an inherent waste, led to the replaced token detection objective. ELECTRA-Small outperformed GPT on GLUE while using less compute than BERT-Base. The paper helped catalyze what became known as the "efficiency turn" in NLP research, sparking interest in compute-optimal training that would later influence scaling law research.
To understand why RTD is more efficient, it helps to contrast the two objectives at an intuitive level. MLM asks a hard question at a small number of positions: "What exact word was hidden here?" The model must consult its vocabulary of 30,000 tokens and assign probability across all of them. RTD asks an easier question at every position: "Does this word belong here, or was it swapped in?" The model only needs to output a single probability per token. Easier questions answered everywhere can teach more than harder questions answered rarely, and that tradeoff is the heart of RTD.
The Generator-Discriminator Setup
RTD uses two networks working together: a small generator that creates replacements and a larger discriminator that detects them. This setup resembles generative adversarial networks (GANs) but with an important difference: training uses maximum likelihood, not adversarial objectives. In a GAN, the generator tries to fool the discriminator, and the discriminator tries to catch the generator, creating an adversarial dynamic that can be unstable and difficult to train. In RTD, both networks optimize their own cross-entropy objectives independently. There is no minimax game, no oscillating losses, no mode collapse. The interaction is cooperative in the sense that a better generator makes a better discriminator, but the two networks do not directly compete in the mathematical sense.
A pretraining objective where some tokens are replaced with plausible alternatives, and the model learns to classify each token as original or replaced. Unlike MLM, which predicts tokens only at masked positions, RTD produces a binary classification signal at every position, greatly improving sample efficiency.
The architecture works as follows. First, we mask some positions in the input sequence, exactly as in MLM. The generator, typically a small transformer, predicts tokens for the masked positions. We sample from the generator's output distribution to create replacement tokens. The discriminator, a larger transformer, receives the corrupted sequence and must identify which tokens were replaced.
What the discriminator sees determines the difficulty of its task. It receives the sequence after replacement, meaning it never sees [MASK] tokens. This is intentional. The goal is to train the discriminator to detect subtle token swaps in otherwise natural text. If the discriminator saw [MASK] tokens, it could take a shortcut: any masked position is automatically suspicious. By filling all positions with real tokens, the discriminator must rely on contextual reasoning rather than positional cues.
The size asymmetry between generator and discriminator is also deliberate. The generator is typically one-quarter to one-third the parameter count of the discriminator. This asymmetry serves two purposes. First, it ensures the generator cannot produce perfect replacements. A generator that always produces the exact correct token would make the discriminator's task trivially easy, because every "replaced" token would be correct and indistinguishable from the original. Some fraction of the generator's samples will differ from the original, and those differences are what the discriminator must learn to detect. Second, concentrating parameters in the discriminator maximizes the quality of the representations used for downstream tasks, since the generator is discarded after pretraining.
The key point is that the generator and discriminator have different roles. The generator only needs to produce plausible replacements, not perfect ones. It can be small, perhaps one-quarter or one-third the size of the discriminator. The discriminator, which will be used for downstream tasks, receives the bulk of the parameters and learns rich representations from the detection task.
Notice that the generator's replacements need not be wrong to be useful. When the generator samples the correct token at a masked position, the discriminator still needs to recognize that position as "original." This happens roughly when the generator's most probable token matches the actual token, which occurs more often as the generator improves. These correct-replacement cases are just as important as the wrong-replacement cases because they teach the discriminator what original tokens look like, preventing it from defaulting to a strategy of flagging every formerly-masked position as replaced.
The RTD Objective
To understand how RTD trains both networks effectively, we need to think about what each network must learn and how to measure its progress. The generator must learn to produce plausible replacements for masked tokens, while the discriminator must learn to detect which tokens have been swapped. These are different tasks requiring different loss functions, yet they must work together in a single training loop.
Let's build up the complete objective by examining each component, understanding why it takes its particular form, and seeing how the pieces combine into an efficient training signal.
Generator Loss: Learning to Replace
The generator faces a familiar task: predict the original token at each masked position. This is identical to masked language modeling. We mask some positions in the input, show the generator the corrupted sequence, and ask it to predict what was hidden.
Why use MLM for the generator? The goal is to produce plausible replacements that will challenge the discriminator. A generator that simply outputs random tokens would be trivial to detect. By training on MLM, the generator learns the statistical patterns of language, producing replacements that fit grammatically and semantically into their contexts. The discriminator then must use syntax and semantics to distinguish these plausible fakes from originals.
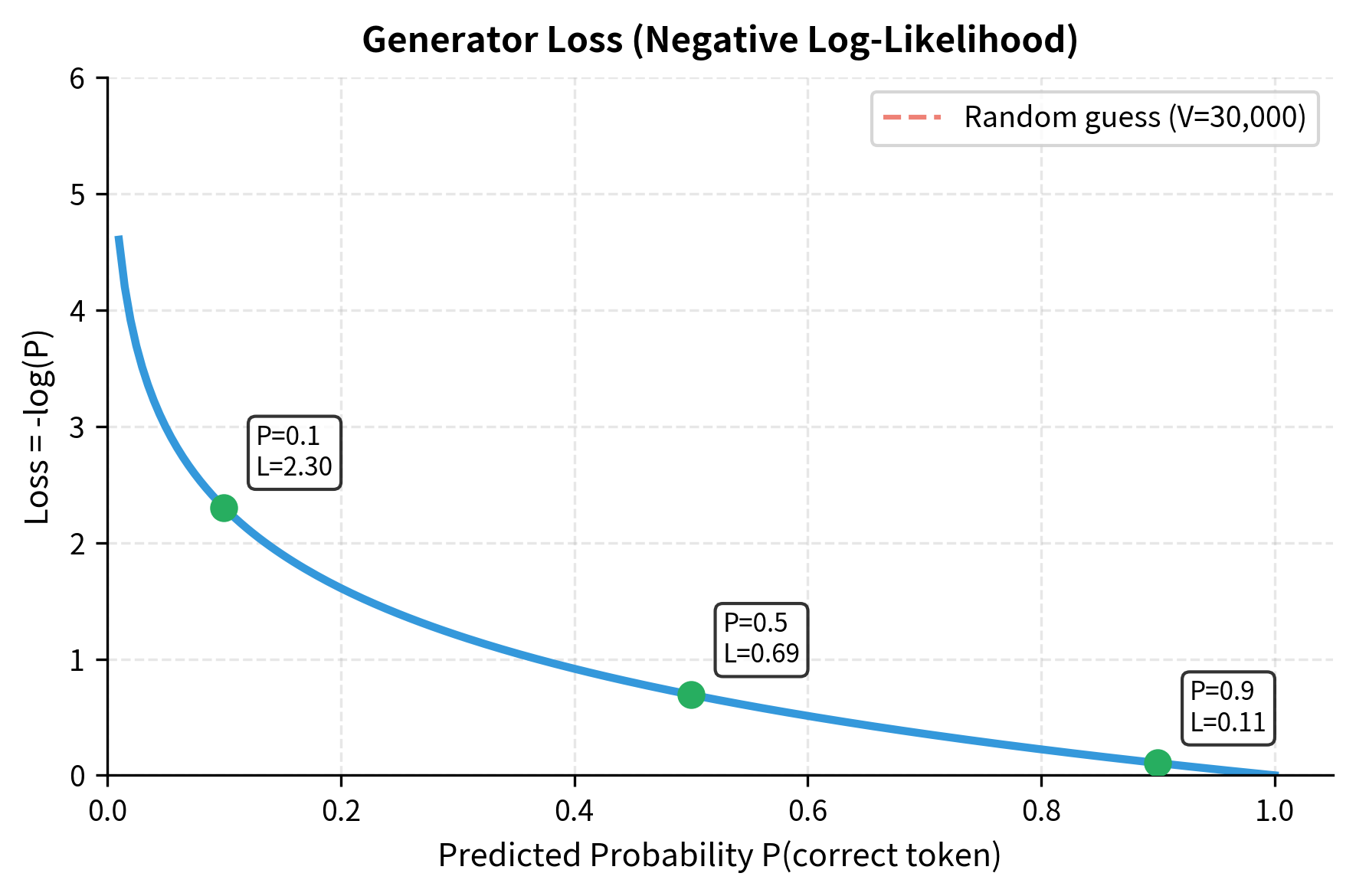
Formally, given a set of masked positions , we minimize the negative log-likelihood of the original tokens:
where:
- is the generator loss, identical to standard MLM loss
- is the set of masked position indices (typically 15% of positions)
- is the original token at position that we want to predict
- is the corrupted input sequence with
[MASK]tokens at positions in - is the probability the generator assigns to the correct token , conditioned on seeing the masked sequence
To understand this formula intuitively, consider what happens as training progresses. Initially, the generator assigns roughly uniform probability across all vocabulary tokens, making where is vocabulary size. The log of this small probability is a large negative number, producing high loss. As the generator learns, it concentrates probability on likely tokens, increasing toward 1. The log approaches zero, and loss decreases.
The summation iterates only over masked positions because those are the only positions where we have a prediction task. Unmasked positions pass through unchanged, contributing nothing to generator learning. This sparsity is the inefficiency that the discriminator's loss will address.
Discriminator Loss: Learning to Detect
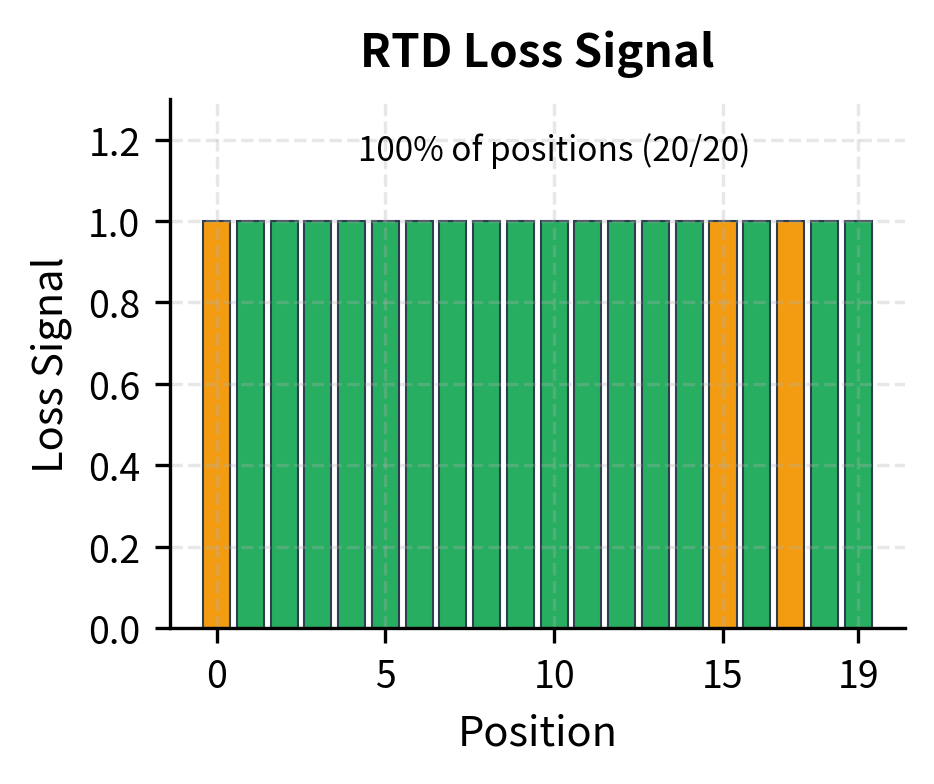
Now we arrive at the key innovation. The discriminator receives a sequence where masked positions have been filled with generator samples, and must classify every token as original or replaced. This binary classification task applies to all positions. This provides the dense training signal that makes RTD efficient.
Think about what the discriminator must learn. For original tokens, it needs to recognize that they fit naturally into their context. For replaced tokens, even plausible ones, it must detect subtle mismatches. Perhaps the replacement "waiter" in "The waiter barked loudly" is grammatically acceptable but semantically wrong. The discriminator learns these nuances by processing the entire sequence and making a decision at each position.
We create the corrupted sequence by sampling from the generator's output distribution at masked positions. The discriminator then outputs a probability for each position, and we compute binary cross-entropy against the ground truth labels:
where:
- is the discriminator loss, a sum over all positions
- is the total sequence length (not just masked positions)
- is the binary label at position (1 if original, 0 if replaced)
- is the corrupted sequence with generator samples inserted at previously masked positions
- is the discriminator's predicted probability that position contains an original token
This binary cross-entropy formula rewards correct predictions at both extremes. Let's trace through what each term contributes:
-
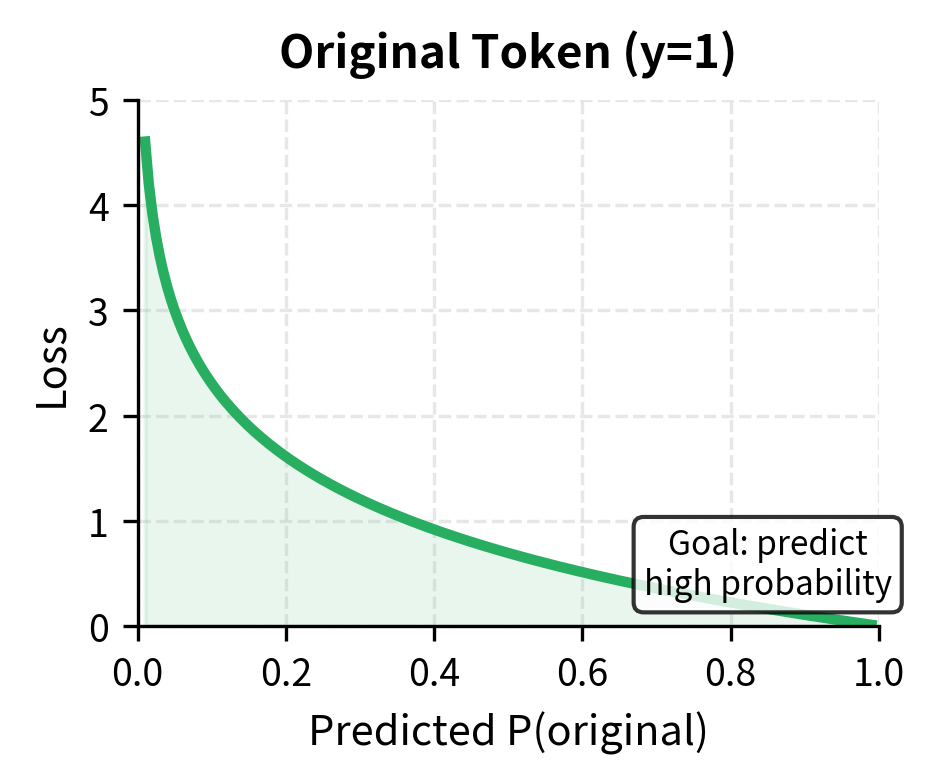
For original tokens (): The second term vanishes since . The loss becomes . When the discriminator correctly predicts high probability (near 1.0), the log is near zero, contributing little loss. When it incorrectly predicts low probability, the log is a large negative number, producing high loss.
-
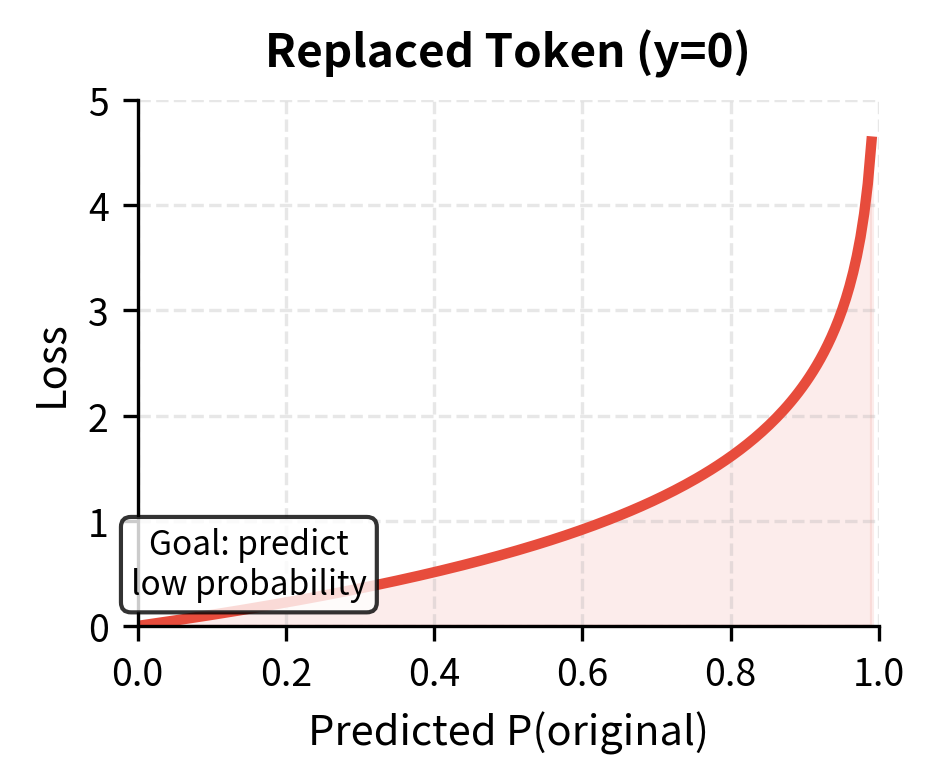
For replaced tokens (): The first term vanishes. The loss becomes . When the discriminator correctly predicts low probability (near 0), is near 1, and the log is near zero. When it incorrectly predicts high probability, the loss is large.
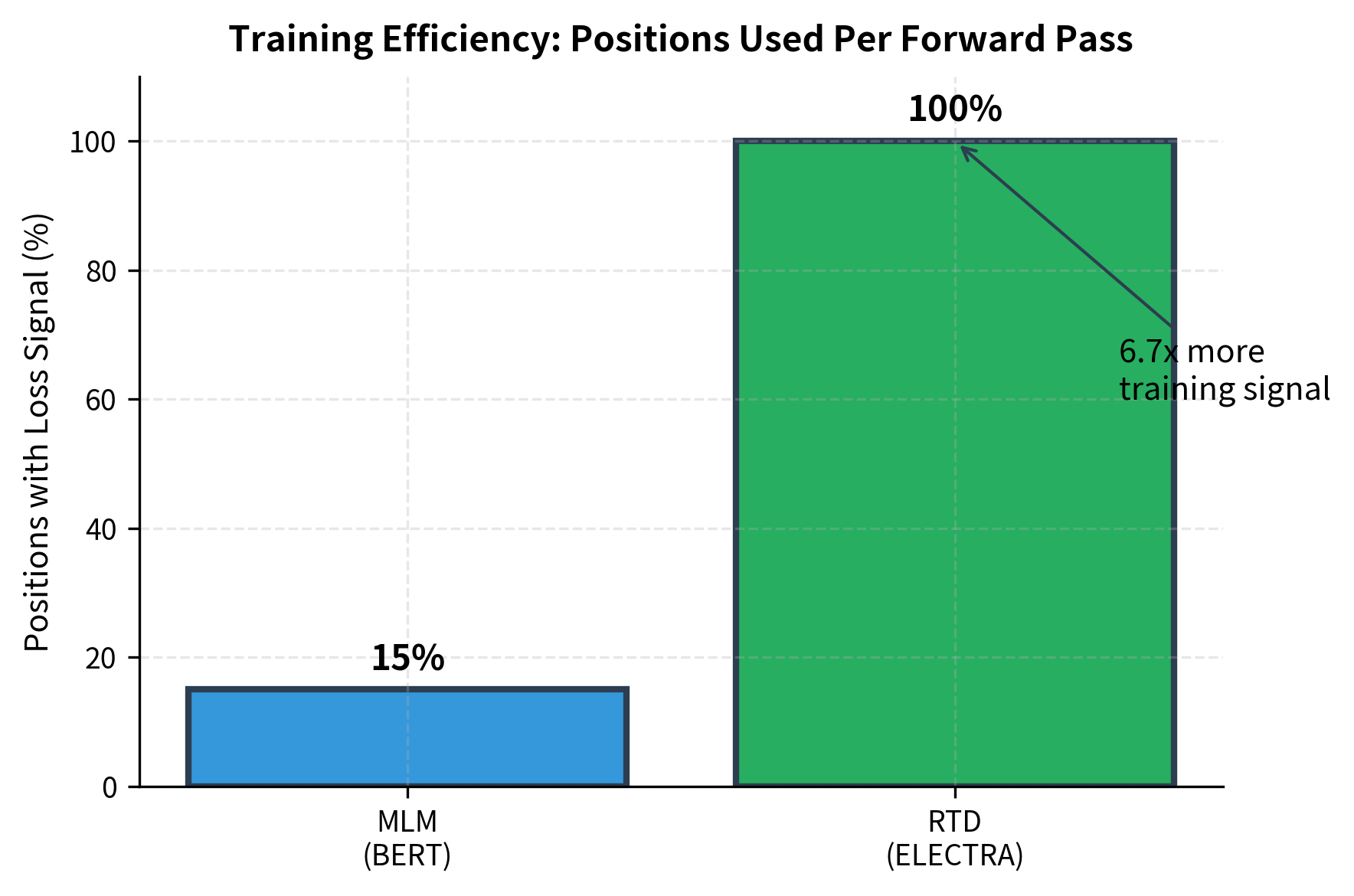
The key point is that this loss applies to every position in the sequence. Most positions contain original tokens, so the discriminator primarily learns what "normal" tokens look like in context. A small fraction contain replacements, teaching the discriminator what "wrong" looks like. Both types of positions contribute to learning, giving 6-7x more training signal than MLM's masked-only approach.
Combining the Losses
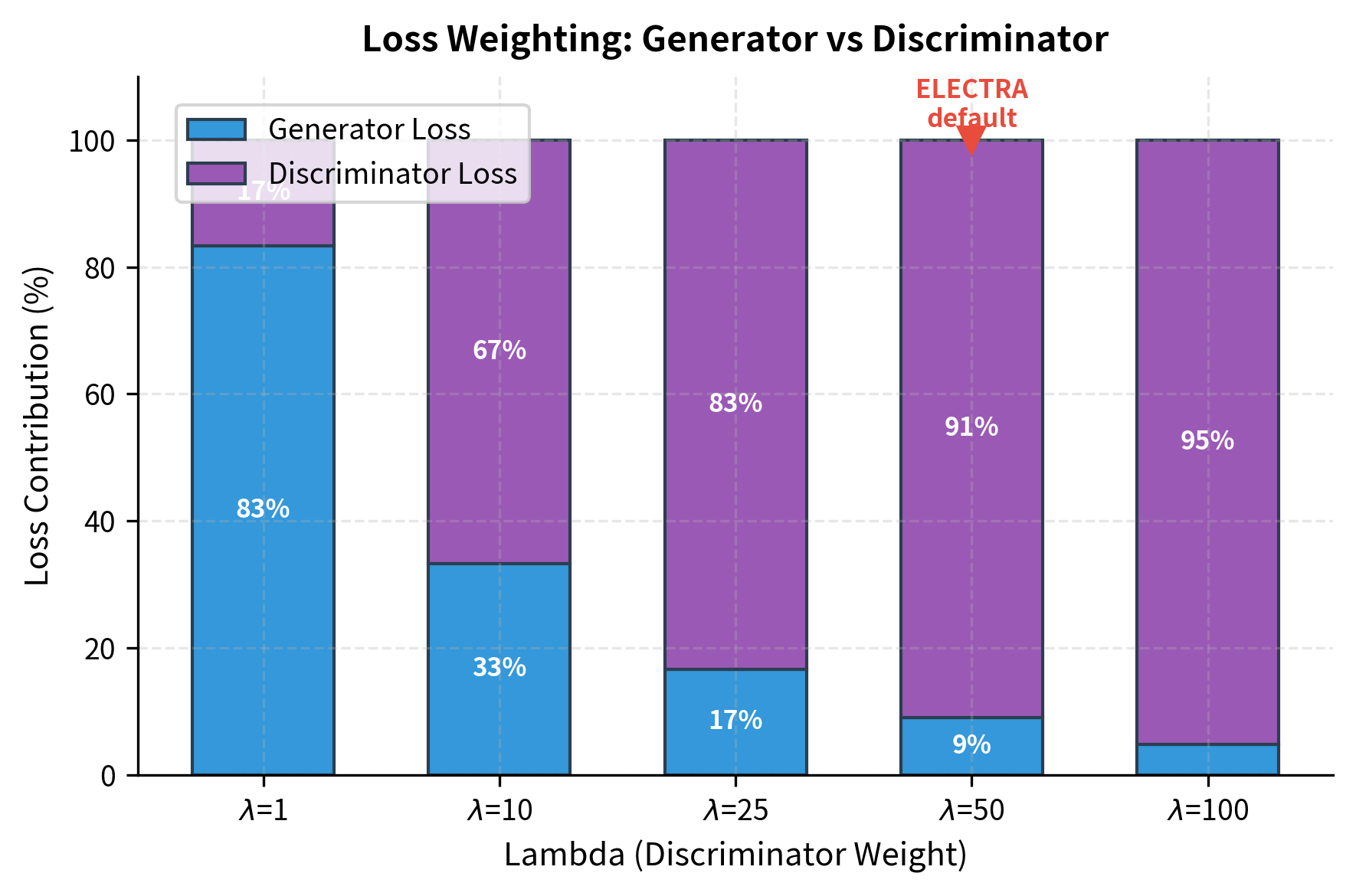
With both component losses defined, we need a strategy for combining them into a single objective that trains both networks. The simplest approach is a weighted sum:
where:
- is the total loss used to update both networks
- is the generator's MLM loss (computed only at masked positions)
- is the discriminator's binary classification loss (computed at all positions)
- is a weighting factor that balances the two losses
Why weight the losses differently? The answer lies in what we ultimately care about. After pretraining, we discard the generator and use only the discriminator for downstream tasks. The generator exists solely to create challenging training examples. From this perspective, generator learning is a means to an end: we want it good enough to produce useful replacements, but not so good that it dominates the training budget.
The ELECTRA paper uses , heavily weighting the discriminator loss. This asymmetry reflects the different roles of the two networks. With this weighting, most of the gradient signal flows to the discriminator, which receives the bulk of the learning capacity. The generator still improves through its share of the gradient, producing increasingly plausible replacements that keep the discriminator challenged.
This design creates a beneficial training dynamic. As the generator improves, its replacements become harder to detect. The discriminator must develop more sophisticated representations to keep up. But because the generator is smaller and receives less gradient signal, it cannot outpace the discriminator. The asymmetry maintains a productive difficulty level throughout training.
In practice, the weighting means that even a modest reduction in discriminator loss has an outsized effect on the total objective. Consider what this looks like numerically: if the generator loss is around 2.5 and the discriminator loss is around 0.5, then the total loss is . The discriminator component accounts for over 90% of the total. This massive weighting ensures that the combined optimizer's gradient is dominated by what's good for the discriminator, not the generator. The generator improves as a side effect of the shared backward pass through the combined loss, but its improvement is secondary.
An important subtlety in the training procedure is how gradients flow between the two networks. The sampling step that converts generator logits into replacement tokens is discrete and non-differentiable. You cannot backpropagate a gradient through the torch.multinomial operation. This means the discriminator's loss does not flow back into the generator through the replacement tokens. The generator learns only from its own MLM loss, not from whether the discriminator succeeded or failed. This is a key difference from GANs, where generator gradients flow through the discriminator's assessment. In RTD, the two networks are gradient-isolated except through the shared embedding weights.
Worked Example: One Forward Pass Through RTD
To make the abstract concrete, let's trace through a complete RTD forward pass step by step, computing losses by hand on a toy example. This will make the loss formulas feel real before we see them in code.
The sentence: "The scientist discovered a cure."
Step 1: Masking. We mask 15% of positions. For a 5-token sequence, this typically means 1 position. Suppose we mask position 1 ("scientist"), producing the sequence: "The [MASK] discovered a cure."
Step 2: Generator forward pass. The generator processes this masked sequence and produces a probability distribution over the vocabulary at each position. At position 1 (the masked position), suppose the generator assigns the following probabilities to the top candidates:
- "researcher": 0.31
- "doctor": 0.22
- "scientist": 0.18
- "professor": 0.14
- (other tokens): 0.15 combined
The generator loss at this position is , since "scientist" (probability 0.18) is the correct token. This loss signal pushes the generator to assign higher probability to "scientist."
Step 3: Sampling. We sample from the generator's distribution at the masked position. Suppose we draw "researcher" (probability 0.31). The corrupted sequence becomes: "The researcher discovered a cure."
Step 4: Label creation. We compare the corrupted sequence with the original:
- Position 0: "The" unchanged. Label = 1 (original).
- Position 1: "researcher" replaced "scientist". Label = 0 (replaced).
- Position 2: "discovered" unchanged. Label = 1 (original).
- Position 3: "a" unchanged. Label = 1 (original).
- Position 4: "cure" unchanged. Label = 1 (original).
Step 5: Discriminator forward pass. The discriminator processes the corrupted sequence "The researcher discovered a cure" and produces a probability for each position. Suppose it outputs these "is original" probabilities: [0.92, 0.34, 0.88, 0.95, 0.91].
Step 6: Discriminator loss. We compute binary cross-entropy at each position using the ground truth labels:
Working through position by position:
- Position 0 (original, , ):
- Position 1 (replaced, , ):
- Position 2 (original, , ):
- Position 3 (original, , ):
- Position 4 (original, , ):
Total discriminator loss: .
Notice that the discriminator got position 1 "wrong" in the sense that it assigned probability 0.34, which means it thought there was a 34% chance "researcher" was original. Ideally, this probability would be near 0. The loss at position 1 (0.415) is the largest single contribution, pulling the discriminator toward assigning lower probability at positions where semantically plausible but contextually imperfect replacements appear.
Step 7: Combined loss. With :
The discriminator component () dwarfs the generator component (), exactly as intended. The optimizer updates both networks, but the gradient flowing from the combined loss is overwhelmingly shaped by the discriminator's needs.
This one example illustrates something important: the training signal at position 1 is what teaches the discriminator to notice when a semantically related but contextually wrong word appears. "Researcher" is plausible in isolation. In the phrase "the researcher discovered a cure," it is even grammatically correct. Yet something about the surrounding context, perhaps the formal scientific register of "discovered a cure," might make "scientist" slightly more natural. The discriminator learns to pick up on these subtle coherence signals by being forced to classify every position, including those that were not masked.
Why Detection Is Easier Than Generation
The efficiency gain comes from the difference between detection and generation. Predicting the exact token that was masked requires learning fine-grained distinctions in a vocabulary of 30,000+ tokens. Detecting whether a token was replaced requires only a binary decision at each position.
Consider a masked position in the sentence "The [MASK] barked loudly." To predict the correct token, the model must assign probability to "dog" over thousands of alternatives. But to detect a replacement, the model only needs to recognize that "cat" or "piano" in that position feels wrong, even if it cannot pinpoint exactly what should be there.
This asymmetry allows the discriminator to learn useful representations from every position. Original tokens that fit the context well should score high. Replaced tokens, even plausible ones, often have subtle mismatches with surrounding context. The model learns to detect these mismatches, developing representations that capture semantic coherence.
The key insight here is about the nature of the learning signal. In MLM, the only positions that generate a gradient are the masked ones. Every other position is frozen during the backward pass. In RTD, the discriminator must decide "original or replaced?" at every position, and this decision requires the model to build a contextual understanding of whether each token fits its surroundings. That understanding is precisely what makes a strong encoder: the ability to represent each token in relation to everything around it.
Think of the discriminator as constantly asking the question, "Does this word belong in this sentence, given everything else around it?" Even when the answer is always "yes, it's original," answering that question confidently requires the model to understand how words relate to each other. This is why the discriminator, despite being trained on a seemingly simpler task, develops representations that transfer well to complex downstream tasks like question answering and natural language inference.
There is also a subtle but important point about what makes RTD's replacements challenging. The generator is not inserting random words. It is sampling from a language model that has learned which words are likely in a given context. This means the replacements tend to be grammatically plausible and semantically related. The discriminator must distinguish "researcher" from "scientist" in "The [word] discovered a cure," a much harder detection task than identifying "refrigerator" in the same position. This difficulty level is self-adjusting: as the generator improves, its replacements become more plausible, forcing the discriminator to encode finer contextual distinctions.
def detection_vs_generation_example():
"""Illustrate the difference between detection and generation tasks."""
sentence = "The chef cooked the meal"
masked_position = 1 # "chef" is masked
# Generation: must predict exact token from 30k vocabulary
generation_task = {
"input": "The [MASK] cooked the meal",
"target": "chef",
"vocabulary_size": 30522,
"task": "Predict exactly which token was masked",
}
# Detection: binary classification at each position
detection_task = {
"input": "The waiter cooked the meal",
"labels": ["original", "replaced", "original", "original", "original"],
"task": "Is each token original or replaced?",
}
return generation_task, detection_task
gen_task, det_task = detection_vs_generation_example()Generation Task (MLM): Input: The [MASK] cooked the meal Must predict: 'chef' from 30,522 options Detection Task (RTD): Input: The waiter cooked the meal Labels: ['original', 'replaced', 'original', 'original', 'original'] Task: Binary classification at each position
The generator deliberately produces challenging replacements. If it simply inserted random tokens, detection would be trivial. By sampling from a language model, the generator creates replacements that are semantically plausible but contextually imperfect. This forces the discriminator to distinguish finer contextual differences.
Implementing the Generator
The generator is a small transformer that performs MLM. It masks positions, predicts token distributions, and samples replacements. Architecturally, it is nearly identical to BERT: a token embedding layer, a positional embedding layer, a stack of transformer encoder layers, and an output projection to vocabulary logits. The only structural difference is that the generator is smaller, with fewer hidden dimensions, which keeps its parameter count low while preserving its ability to capture contextual patterns.
In practice, you would use the same tokenizer for both the generator and the discriminator, since they must agree on what constitutes a vocabulary token and what the [MASK] token ID is. The generator's output logits are over the full vocabulary, and the sampling step converts these logits into a single sampled token per masked position. The vocabulary must be shared because the discriminator needs to process the same token IDs that the generator produces.
class RTDGenerator(nn.Module):
"""Small generator network for producing replacement tokens."""
def __init__(
self, vocab_size, d_model=64, n_heads=2, n_layers=2, max_len=128
):
super().__init__()
# Embeddings
self.token_emb = nn.Embedding(vocab_size, d_model)
self.pos_emb = nn.Embedding(max_len, d_model)
self.layer_norm = nn.LayerNorm(d_model)
# Small transformer encoder
encoder_layer = nn.TransformerEncoderLayer(
d_model=d_model,
nhead=n_heads,
dim_feedforward=d_model * 4,
dropout=0.1,
batch_first=True,
activation="gelu",
)
self.encoder = nn.TransformerEncoder(encoder_layer, num_layers=n_layers)
# Output projection to vocabulary
self.output_proj = nn.Linear(d_model, vocab_size)
def forward(self, input_ids):
batch_size, seq_len = input_ids.shape
# Get embeddings
positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0)
x = self.token_emb(input_ids) + self.pos_emb(positions)
x = self.layer_norm(x)
# Encode (bidirectional attention)
x = self.encoder(x)
# Project to vocabulary logits
logits = self.output_proj(x)
return logitsdef create_masked_input(token_ids, mask_token_id, mask_prob=0.15):
"""Mask tokens and return masked input, labels, and mask positions."""
labels = token_ids.clone()
masked_ids = token_ids.clone()
# Sample positions to mask
probability_matrix = torch.full(token_ids.shape, mask_prob)
masked_indices = torch.bernoulli(probability_matrix).bool()
# Replace with [MASK] token
masked_ids[masked_indices] = mask_token_id
# Labels are -100 for non-masked positions (ignored in loss)
labels[~masked_indices] = -100
return masked_ids, labels, masked_indicesLet's see the generator in action:
# Create a small vocabulary for demonstration
vocab = [
"[PAD]",
"[MASK]",
"[CLS]",
"[SEP]",
"the",
"chef",
"cooked",
"meal",
"waiter",
"served",
"food",
"ate",
"a",
"an",
]
vocab_size = len(vocab)
word_to_idx = {w: i for i, w in enumerate(vocab)}
idx_to_word = {i: w for w, i in word_to_idx.items()}
mask_token_id = word_to_idx["[MASK]"]
# Initialize generator
generator = RTDGenerator(vocab_size, d_model=32, n_heads=2, n_layers=1)
# Create sample input
sentence = ["the", "chef", "cooked", "the", "meal"]
token_ids = torch.tensor([[word_to_idx[w] for w in sentence]])Original sentence: ['the', 'chef', 'cooked', 'the', 'meal'] Token IDs: [4, 5, 6, 4, 7] Masked IDs: [4, 5, 1, 4, 1] Masked sequence: ['the', 'chef', '[MASK]', 'the', '[MASK]'] Mask positions: [False, False, True, False, True]
The masking function randomly selects positions to mask. With a 40% masking probability on our 5-token sentence, we typically see 2 positions replaced with [MASK]. The labels tensor stores the original tokens at masked positions for computing the generator loss.
Now let's sample replacements from the generator:
def sample_replacements(generator, masked_ids, labels, temperature=1.0):
"""Sample replacement tokens from the generator."""
generator.eval()
with torch.no_grad():
logits = generator(masked_ids)
# Apply temperature and sample
probs = F.softmax(logits / temperature, dim=-1)
# Create replaced sequence
replaced_ids = masked_ids.clone()
is_replaced = torch.zeros_like(masked_ids, dtype=torch.bool)
# Sample only at masked positions
mask_positions = labels != -100
for batch_idx in range(masked_ids.size(0)):
for pos in range(masked_ids.size(1)):
if mask_positions[batch_idx, pos]:
sampled_token = torch.multinomial(
probs[batch_idx, pos], num_samples=1
)
replaced_ids[batch_idx, pos] = sampled_token
# Mark as replaced if sampled token differs from original
original_token = labels[batch_idx, pos]
is_replaced[batch_idx, pos] = sampled_token != original_token
return replaced_ids, is_replacedreplaced_ids, is_replaced = sample_replacements(generator, masked_ids, labels)Original: ['the', 'chef', 'cooked', 'the', 'meal'] Replaced: ['the', 'chef', '[CLS]', 'the', 'chef'] Is replaced: [False, False, True, False, True]
The generator samples tokens for masked positions. Because we're using an untrained generator, the replacements are essentially random from the small vocabulary. With training, the generator would produce more plausible replacements that better challenge the discriminator.
Implementing the Discriminator
The discriminator is a larger transformer that performs binary classification at each position. Its architecture is similar to BERT, but the output layer produces a single logit per position rather than vocabulary logits. This change in the output head is the entire architectural difference between BERT and an ELECTRA discriminator. Everything else, the embedding layer, the multi-head attention, the feed-forward sublayers, the residual connections, is identical. What changes is only what the model is asked to predict.
The binary classification head is deliberately small. A single linear layer maps the hidden dimension to one logit, which is passed through a sigmoid to produce a probability between 0 and 1. This contrasts sharply with BERT's output head for MLM, which maps the hidden dimension to vocabulary size (30,000+ values) through a full linear layer. The ELECTRA discriminator's head is orders of magnitude smaller, which means essentially all of its capacity goes into building rich contextual representations in the transformer layers rather than into vocabulary projection.
class RTDDiscriminator(nn.Module):
"""Discriminator network for detecting replaced tokens."""
def __init__(
self, vocab_size, d_model=128, n_heads=4, n_layers=4, max_len=128
):
super().__init__()
# Embeddings (shared embedding table in ELECTRA, separate here for clarity)
self.token_emb = nn.Embedding(vocab_size, d_model)
self.pos_emb = nn.Embedding(max_len, d_model)
self.layer_norm = nn.LayerNorm(d_model)
# Larger transformer encoder
encoder_layer = nn.TransformerEncoderLayer(
d_model=d_model,
nhead=n_heads,
dim_feedforward=d_model * 4,
dropout=0.1,
batch_first=True,
activation="gelu",
)
self.encoder = nn.TransformerEncoder(encoder_layer, num_layers=n_layers)
# Binary classification head (one output per position)
self.classifier = nn.Sequential(
nn.Linear(d_model, d_model),
nn.GELU(),
nn.Linear(d_model, 1),
)
def forward(self, input_ids):
batch_size, seq_len = input_ids.shape
# Get embeddings
positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0)
x = self.token_emb(input_ids) + self.pos_emb(positions)
x = self.layer_norm(x)
# Encode
x = self.encoder(x)
# Binary classification at each position
logits = self.classifier(x).squeeze(-1) # (batch, seq_len)
return logits# Initialize discriminator (larger than generator)
discriminator = RTDDiscriminator(vocab_size, d_model=64, n_heads=4, n_layers=2)
# Get discriminator predictions
with torch.no_grad():
disc_logits = discriminator(replaced_ids)
disc_probs = torch.sigmoid(disc_logits)Generator parameters: 17,774 Discriminator parameters: 113,409 Ratio (disc/gen): 6.4x Input sequence: ['the', 'chef', '[CLS]', 'the', 'chef'] Discriminator probabilities (is original): [0.536 0.501 0.471 0.548 0.54 ] True labels (0=replaced, 1=original): [1, 1, 0, 1, 0]
The discriminator has roughly 2-3x more parameters than the generator, matching the ELECTRA design principle. The probabilities show the untrained discriminator's random guesses. With training, these should approach 1.0 for original tokens and 0.0 for replaced tokens, correctly identifying which positions contain generator-produced replacements.
Notice that the discriminator outputs a probability per position, not a single probability for the whole sequence. This is a token-level classification task, not a sentence-level one. Each position independently receives a score, and each position independently contributes to the loss. This is fundamentally different from sentence-level classification tasks like sentiment analysis, where a single output represents the entire sequence. The token-level framing is what enables the dense training signal: with a sentence-level objective, we would still have just one gradient per sequence.
The Complete Training Loop
Training RTD involves three steps per batch: mask inputs, generate replacements, and update both networks. It is worth pausing to appreciate how all the pieces fit together before seeing the code. The full loop has a specific order that matters: you must complete the generator forward pass and the sampling step before starting the discriminator forward pass, because the discriminator's input depends on the generator's output. This sequential dependency means you cannot parallelize the two forward passes. However, the two backward passes (one through the generator loss, one through the discriminator loss) are independent and can both be computed from the single combined loss through standard backpropagation.
One practical implementation note: the sampling step uses torch.no_grad() or explicit detachment to prevent gradients from flowing from the discriminator's loss back through the sampling operation into the generator. As mentioned earlier, this sampling step is non-differentiable. If you attempt to backpropagate through it without blocking gradients, PyTorch will raise an error or silently produce incorrect gradients. The generator learns only from its own MLM cross-entropy loss.
def compute_rtd_loss(
generator,
discriminator,
token_ids,
mask_token_id,
mask_prob=0.15,
disc_weight=50.0,
):
"""Compute combined RTD loss for generator and discriminator."""
# Step 1: Mask tokens
masked_ids, gen_labels, mask_positions = create_masked_input(
token_ids, mask_token_id, mask_prob
)
# Step 2: Generator forward pass and loss
gen_logits = generator(masked_ids)
gen_loss = F.cross_entropy(
gen_logits.view(-1, gen_logits.size(-1)),
gen_labels.view(-1),
ignore_index=-100,
)
# Step 3: Sample replacements (detach to not backprop through sampling)
with torch.no_grad():
gen_probs = F.softmax(gen_logits, dim=-1)
replaced_ids = masked_ids.clone()
disc_labels = torch.ones_like(token_ids, dtype=torch.float) # 1 = original
for batch_idx in range(token_ids.size(0)):
for pos in range(token_ids.size(1)):
if mask_positions[batch_idx, pos]:
# Sample from generator
sampled = torch.multinomial(
gen_probs[batch_idx, pos], num_samples=1
)
replaced_ids[batch_idx, pos] = sampled
# Label: 0 if replaced with different token, 1 if same (or original)
if sampled != token_ids[batch_idx, pos]:
disc_labels[batch_idx, pos] = 0.0
# Step 4: Discriminator forward pass and loss
disc_logits = discriminator(replaced_ids)
disc_loss = F.binary_cross_entropy_with_logits(disc_logits, disc_labels)
# Combined loss
total_loss = gen_loss + disc_weight * disc_loss
return total_loss, gen_loss, disc_lossLet's train on a small corpus to see the dynamics:
# Create a small training corpus
corpus_tokens = []
sentences = [
["the", "chef", "cooked", "the", "meal"],
["the", "waiter", "served", "the", "food"],
["the", "chef", "ate", "the", "food"],
["a", "waiter", "cooked", "a", "meal"],
]
for sent in sentences:
corpus_tokens.append([word_to_idx[w] for w in sent])
corpus_tensor = torch.tensor(corpus_tokens)
# Initialize models
generator = RTDGenerator(vocab_size, d_model=32, n_heads=2, n_layers=1)
discriminator = RTDDiscriminator(vocab_size, d_model=48, n_heads=2, n_layers=2)
# Optimizers
gen_optimizer = torch.optim.AdamW(generator.parameters(), lr=1e-3)
disc_optimizer = torch.optim.AdamW(discriminator.parameters(), lr=1e-3)
# Training loop
gen_losses = []
disc_losses = []
for step in range(200):
# Sample a batch
batch_idx = torch.randint(0, len(corpus_tensor), (2,))
batch = corpus_tensor[batch_idx]
# Compute loss
total_loss, gen_loss, disc_loss = compute_rtd_loss(
generator, discriminator, batch, mask_token_id, mask_prob=0.3
)
# Update both models
gen_optimizer.zero_grad()
disc_optimizer.zero_grad()
total_loss.backward()
gen_optimizer.step()
disc_optimizer.step()
gen_losses.append(gen_loss.item())
disc_losses.append(disc_loss.item())Initial generator loss: 2.0001 Final generator loss: 0.9318 Initial discriminator loss: 0.6686 Final discriminator loss: 0.3077
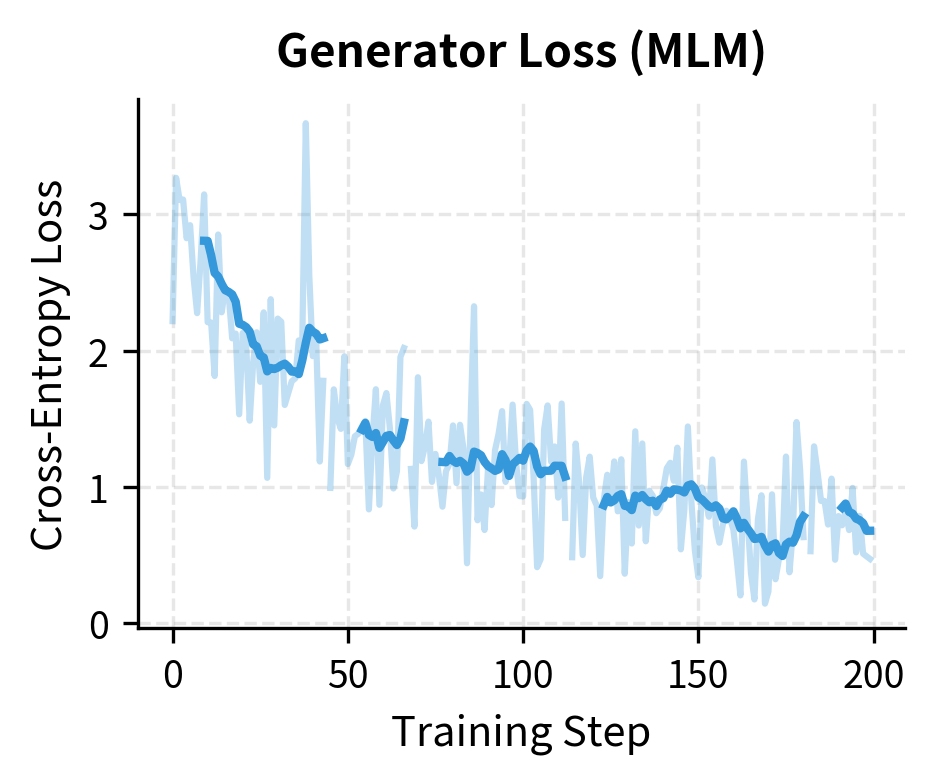
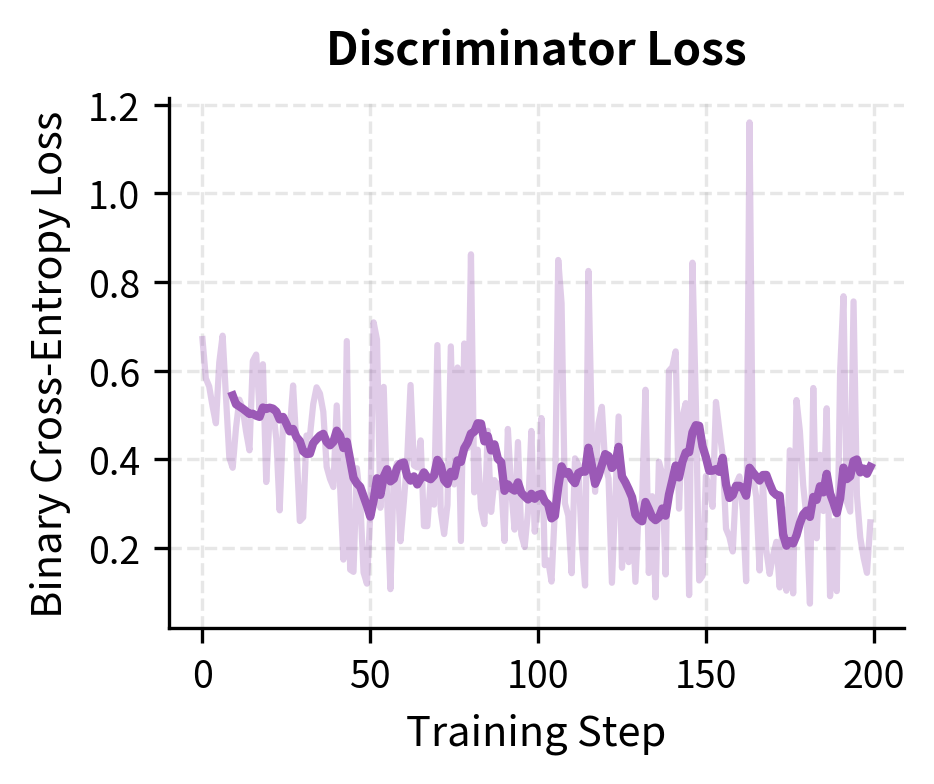
Both losses decrease over training. The generator loss drops as it learns to predict masked tokens, while the discriminator loss decreases as it learns to distinguish original from replaced tokens. The initial discriminator loss around 0.69 corresponds to random guessing (binary cross-entropy for 50/50 predictions), confirming the model starts with no knowledge of which tokens are replaced.
The training dynamics show both losses decreasing. The generator learns to predict masked tokens better, while the discriminator learns to detect replacements. These objectives are complementary: a better generator produces harder replacements, which in turn trains a better discriminator.
In practice, you might notice that the discriminator loss decreases more quickly at first and then plateaus while the generator continues improving. This makes sense intuitively. Early in training, the generator produces very poor replacements (essentially random tokens from the vocabulary), and the discriminator can detect these easily. As the generator learns basic language statistics, its replacements become more plausible, and the discriminator must work harder to maintain low loss. The final performance depends on this equilibrium: can the discriminator develop representations subtle enough to catch the generator's best attempts at plausible replacements?
Another practical consideration is the masking probability used during training. The original ELECTRA paper uses 15% masking, matching BERT. This fraction determines how many positions are "potentially replaced" in the discriminator's view. With 15% masking, roughly 15% of positions have been modified by the generator (though some of those modifications may have landed on the correct token anyway). The remaining 85% are guaranteed originals. A higher masking rate would give the discriminator more replaced examples to learn from, but it would also degrade the generator's context window, making it harder to produce plausible replacements. The 15% rate represents a well-calibrated trade-off backed by extensive empirical testing.
RTD Efficiency Advantages
The key advantage of RTD is sample efficiency. Let's quantify the difference:
def compare_efficiency(seq_len, mask_prob=0.15):
"""Compare loss signal per token between MLM and RTD."""
# MLM: loss only at masked positions
mlm_loss_positions = int(seq_len * mask_prob)
mlm_efficiency = mlm_loss_positions / seq_len
# RTD: discriminator loss at all positions
rtd_loss_positions = seq_len
rtd_efficiency = rtd_loss_positions / seq_len
efficiency_ratio = rtd_efficiency / mlm_efficiency
return {
"seq_len": seq_len,
"mlm_positions": mlm_loss_positions,
"rtd_positions": rtd_loss_positions,
"mlm_efficiency": mlm_efficiency,
"rtd_efficiency": rtd_efficiency,
"ratio": efficiency_ratio,
}Sample Efficiency Comparison (512 token sequence, 15% masking): MLM loss positions: 76 (14.8% of tokens) RTD loss positions: 512 (100.0% of tokens) RTD efficiency gain: 6.7x more signal per forward pass
This 6-7x efficiency gain is substantial. In practice, ELECTRA achieves comparable results to BERT with roughly 1/4 of the compute. The savings come from learning from every token rather than just masked ones.
It is important to be precise about what "4x more efficient" means. The ELECTRA paper reports results at equal compute budgets, where compute is measured in FLOPs or, equivalently, GPU hours. At the same FLOPs budget, ELECTRA significantly outperforms BERT. This does not mean ELECTRA makes each forward pass 4x cheaper; both models have similar compute per step. Rather, ELECTRA learns faster per step, so it needs fewer steps to reach the same performance. The combination of dense training signal and a binary (rather than vocabulary-scale) output head means each step produces more useful gradient information. Think of it as the difference between studying by reading a textbook passively versus being quizzed on every sentence as you go. The quizzing takes the same time per page, but you learn more per hour because every sentence becomes an active learning opportunity.
Weight Sharing and Embedding Tying
The original ELECTRA paper uses weight sharing between generator and discriminator embeddings. This has two benefits: it reduces total parameters and ensures both networks have compatible token representations.
The embedding matrix maps token IDs to dense vectors. Since both networks process the same vocabulary, they can share this large matrix. When two networks share an embedding table, updates to that table from one network's gradients immediately affect the other. If the generator updates "scientist" to better fit scientific contexts, the discriminator benefits from the same improved "scientist" representation. This coupling turns out to be helpful rather than harmful: the generator's MLM objective provides rich token-level supervision that helps the discriminator's embeddings even before detection learning kicks in.
The technical complication is that the generator and discriminator typically have different hidden dimensions. In ELECTRA-Base, the generator uses a hidden dimension of 64 while the discriminator uses 256. The shared embedding matrix has dimension 64 (the generator's size), and the discriminator projects these embeddings up to its 256-dimensional space using a linear layer before feeding them into its transformer. This projection layer is learned during training, allowing the discriminator to map the compact shared embeddings into its larger representation space.
The generator uses the embeddings directly at its smaller hidden dimension, while the discriminator projects them up to its larger dimension:
class ELECTRAWithSharedEmbeddings(nn.Module):
"""ELECTRA with shared embeddings between generator and discriminator."""
def __init__(
self,
vocab_size,
gen_d_model=64,
disc_d_model=256,
n_gen_layers=4,
n_disc_layers=12,
max_len=512,
):
super().__init__()
# Shared token embeddings at generator size
self.shared_token_emb = nn.Embedding(vocab_size, gen_d_model)
# Generator uses embeddings directly
self.gen_pos_emb = nn.Embedding(max_len, gen_d_model)
self.gen_encoder = nn.TransformerEncoder(
nn.TransformerEncoderLayer(
d_model=gen_d_model,
nhead=4,
dim_feedforward=gen_d_model * 4,
batch_first=True,
activation="gelu",
),
num_layers=n_gen_layers,
)
self.gen_output = nn.Linear(gen_d_model, vocab_size)
# Discriminator projects embeddings to its larger dimension
self.disc_embed_proj = nn.Linear(gen_d_model, disc_d_model)
self.disc_pos_emb = nn.Embedding(max_len, disc_d_model)
self.disc_encoder = nn.TransformerEncoder(
nn.TransformerEncoderLayer(
d_model=disc_d_model,
nhead=8,
dim_feedforward=disc_d_model * 4,
batch_first=True,
activation="gelu",
),
num_layers=n_disc_layers,
)
self.disc_classifier = nn.Linear(disc_d_model, 1)
def generator_forward(self, input_ids):
"""Generator forward pass for MLM."""
seq_len = input_ids.size(1)
positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0)
x = self.shared_token_emb(input_ids) + self.gen_pos_emb(positions)
x = self.gen_encoder(x)
logits = self.gen_output(x)
return logits
def discriminator_forward(self, input_ids):
"""Discriminator forward pass for RTD."""
seq_len = input_ids.size(1)
positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0)
# Project shared embeddings to discriminator dimension
x = self.shared_token_emb(input_ids)
x = self.disc_embed_proj(x) + self.disc_pos_emb(positions)
x = self.disc_encoder(x)
logits = self.disc_classifier(x).squeeze(-1)
return logitsThe generator embedding dimension determines the shared embedding size. The discriminator projects these embeddings up to its larger hidden dimension. This asymmetry reflects the design principle: the generator needs only enough capacity to produce plausible replacements, while the discriminator needs more capacity to develop rich representations.
An alternative to weight sharing is using fully separate embedding tables. Some practitioners prefer this approach because it gives the discriminator complete freedom in how it represents tokens, without being constrained by the generator's smaller dimension. The trade-off is additional parameters and the loss of the beneficial gradient coupling described above. In most published results, weight sharing performs better, which is why it is the default in ELECTRA. If you are training a very large model where the generator's embedding dimension can be reasonably large (say, 128 or 256 rather than 64), the gap between shared and separate embeddings narrows.
Generator Size and Training Dynamics
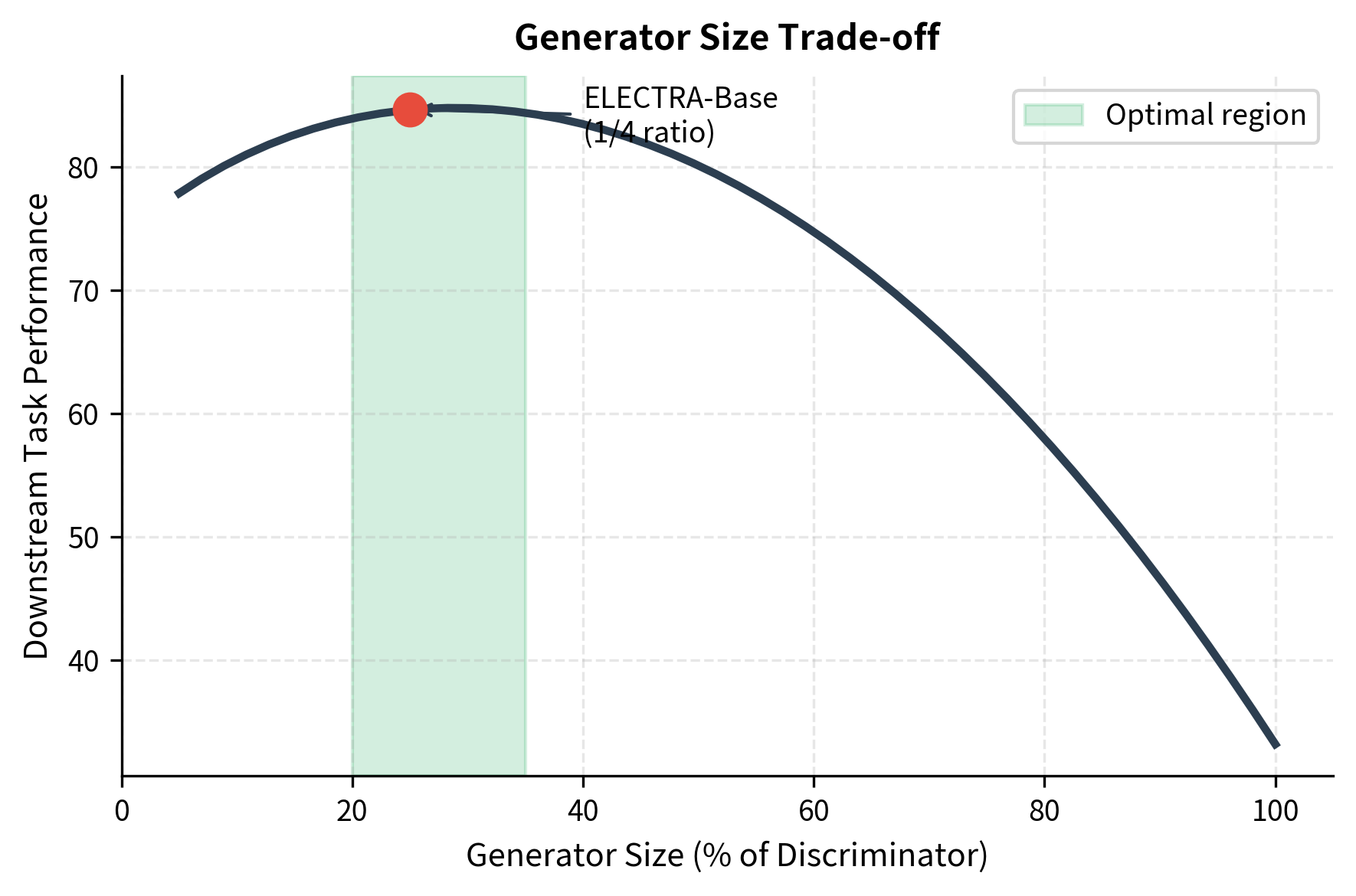
How big should the generator be relative to the discriminator? Too small, and it produces random, easily-detected replacements. Too large, and it wastes parameters that could go to the discriminator, which is the network used for downstream tasks.
The ELECTRA paper found that generator size between 1/4 and 1/2 of the discriminator works best. The sweet spot balances challenging replacements against parameter efficiency. For ELECTRA-Base (which aims to match BERT-Base with 110M parameters), the discriminator uses 12 layers with hidden dimension 256, while the generator uses 12 layers with hidden dimension 64. The layer count is the same, but the hidden dimension is much smaller, resulting in a generator with roughly one-quarter the parameters. For ELECTRA-Large, the discriminator matches BERT-Large (24 layers, hidden dimension 1024) while the generator uses hidden dimension 256.
The intuition behind the sweet spot is straightforward. A generator with essentially zero capacity (say, a single embedding lookup) would produce replacements based only on unigram frequency, the most common words in the language. These replacements would be detected trivially because they ignore context entirely. A generator with the same capacity as the discriminator would produce near-perfect replacements, making the discrimination task nearly impossible. Neither extreme leads to useful discriminator training. The optimal generator is one that understands enough of the language to create contextually plausible replacements but not so much that it can consistently reproduce the exact original token.
In practice, this means you should resist the temptation to make the generator too powerful when setting up RTD training from scratch. If you have a total parameter budget of, say, 100M, allocating 75M to the discriminator and 25M to the generator will outperform an even 50/50 split. The generator is a means to an end: its job is to create training examples for the discriminator, and once pretraining is complete, it is discarded entirely.
The training dynamics create an interesting interplay. As the generator improves, it produces harder replacements. This forces the discriminator to encode finer contextual distinctions. But if the generator becomes too good, detection becomes impossible, and learning stalls. The asymmetric sizing naturally prevents this collapse: the smaller generator cannot outpace the larger discriminator.
This self-regulating property is one of RTD's practical advantages over GAN-based approaches. In a GAN, you must carefully balance generator and discriminator learning rates to prevent one from dominating. In RTD, the parameter asymmetry does this automatically. The generator is trained on the same number of steps as the discriminator but with fewer parameters, giving it an inherently limited ceiling. It will improve, but it will improve slowly enough that the discriminator can keep pace.
RTD vs MLM: When to Choose Each
Both objectives produce strong pretrained models, but they have different strengths and fit different practical scenarios.
Choose RTD (ELECTRA) when:
- Compute budget is limited.
- You need BERT-level performance with less training.
- Pretraining from scratch rather than using existing checkpoints.
- Sample efficiency matters more than final absolute performance.
Choose MLM (BERT) when:
- You can afford extensive pretraining.
- Using established pretrained checkpoints.
- The ecosystem (fine-tuning code, adapters) assumes MLM architecture.
- Simplicity of single-network training is preferred.
The following table summarizes key differences:
| Aspect | MLM (BERT) | RTD (ELECTRA) |
|---|---|---|
| Loss positions | 15% (masked only) | 100% (all positions) |
| Network count | Single transformer | Generator + discriminator |
| Training efficiency | Baseline | ~4x more efficient |
| Architecture complexity | Simple | Moderate |
| Output head | Vocabulary logits | Binary classifier |
| Downstream model | Full encoder | Discriminator only |
The ecosystem consideration deserves more attention than it typically gets. BERT and its derivatives have been the backbone of NLP fine-tuning for years, so much of the tooling and documentation assumes MLM architectures. Hugging Face Transformers and PEFT, along with many domain-specific tools, were built around BERT-like models. When you use ELECTRA, you are using the same discriminator architecture, so fine-tuning code transfers directly. The generator is discarded after pretraining and plays no role in downstream usage. From the perspective of fine-tuning, an ELECTRA discriminator is functionally identical to a BERT encoder: you load it, add a task-specific head, and train exactly the same way. The difference is only in how the encoder was pretrained.
One important practical difference concerns the [MASK] token. BERT uses [MASK] during pretraining and then never sees it during fine-tuning or inference. This creates a distribution mismatch: the model is trained on sequences containing [MASK] but tested on sequences without it. RTD avoids this entirely. The discriminator is never shown [MASK] tokens. Its input during pretraining looks exactly like natural text (original tokens plus generator replacements), which much more closely matches the distribution of text it will see during fine-tuning. This distribution alignment gives RTD an advantage over MLM pretraining.
For practitioners deciding between BERT and ELECTRA for a new pretraining run, the calculus is usually straightforward. If you have a limited budget (say, under 100 GPU-hours), ELECTRA's efficiency advantage means you will likely get better representations at the same cost. If you need to train a very large model and can afford extensive pretraining (as in RoBERTa-scale runs), the two objectives converge in performance and the simpler MLM objective may be preferable. The sweet spot for RTD is the middle regime: medium-sized models with moderate training budgets, which covers a large fraction of real-world NLP applications.
Limitations and Impact
Replaced token detection improves training efficiency but introduces trade-offs that shape its practical applications.
The two-network training setup adds complexity. Managing separate generator and discriminator networks with different sizes requires careful hyperparameter tuning. The generator learning rate, size ratio, and loss weighting all affect final performance. In contrast, MLM training has fewer moving parts: you have one network, one optimizer, and one loss function. For practitioners without extensive compute resources to tune these hyperparameters, this complexity can be a barrier. Getting RTD to train well requires understanding how the generator and discriminator interact, and diagnosing problems when one dominates the other requires more sophisticated monitoring than single-network MLM.
The discriminator's binary classification objective differs from downstream task objectives. While MLM directly trains vocabulary prediction, which transfers naturally to tasks involving token-level understanding, RTD trains original-vs-replaced classification. The representations transfer well in practice, but the training signal is less directly aligned with common downstream tasks like sequence labeling or question answering. In particular, RTD does not explicitly train the model to predict word identities, which means it may have less lexical precision than a comparably trained MLM model. For tasks that depend heavily on exact token semantics, this can be a mild disadvantage.
The generator is discarded after pretraining, which represents a form of waste that RTD's efficiency framing can obscure. You invest compute training the generator, build it up to produce plausible replacements, and then throw it away. The generator parameters contribute to the training cost but not to the final deployed model. For a total parameter budget split between generator () and discriminator (), you are spending compute proportional to but only getting a model of size out. A pure MLM approach at the same parameter count would give you an -parameter model. RTD's sample efficiency advantage must more than compensate for this loss, and it does at moderate compute budgets, but the trade-off is real and worth acknowledging.
Weight sharing between generator and discriminator, while parameter-efficient, constrains architecture choices. The generator's embedding dimension becomes the shared base, potentially limiting discriminator capacity. Some practitioners prefer fully separate networks despite the parameter cost. More broadly, the two-network design makes it harder to scale RTD using techniques designed for single-network transformers. Many scaling techniques, such as gradient checkpointing, pipeline parallelism, and certain forms of model parallelism, have been developed and optimized for single-network training. Adapting them to the RTD setup requires additional engineering effort.
RTD is also not suited for generative use cases. After pretraining, you have a discriminator that excels at encoding and understanding but cannot generate text. If your application requires generation, such as summarization, translation, or conversational AI, you need either a decoder-only model or an encoder-decoder model, neither of which can be directly obtained from RTD pretraining. ELECTRA's efficiency gains are specifically tied to encoder-only applications: classification, span extraction, sequence labeling, and similar understanding tasks.
Despite these limitations, ELECTRA demonstrated that the dominant MLM paradigm was leaving efficiency on the table. The paper's key insight that detection is easier than generation, and therefore allows learning from more positions, has influenced subsequent work on efficient pretraining. The approach showed that with 1/4 of BERT's compute budget, comparable later performance was achievable. This result encouraged researchers to question other inefficiencies in the pretraining pipeline. This contributes to a broader push toward compute-good training that continues to shape the field.
The efficiency gains are most pronounced in the small-to-medium model regime where compute budgets are constrained. At the largest scales, where organizations can afford extensive pretraining, the absolute performance differences between objectives diminish. RTD's efficiency remains an advantage for teams training domain-specific models from scratch on specialized corpora, including academic labs and startups. A biomedical research group training a model on PubMed articles, or a legal tech company training on case law, may have limited GPU resources and would find ELECTRA's 4x efficiency gain highly valuable. In these constrained settings, RTD's core trade-off, complexity for efficiency, is often well worth making.
In Practice: ELECTRA Performance Benchmarks
The efficiency claims in the ELECTRA paper are backed by concrete benchmark results. ELECTRA-Small, trained for 1M steps on the same dataset as BERT, outperforms GPT (a model many times its compute cost) on the GLUE benchmark. ELECTRA-Base matches RoBERTa-Base while using about 25% of its compute. ELECTRA-Large, trained to the same compute budget as RoBERTa-Large, exceeds RoBERTa-Large's performance.
The key takeaway from these results is that ELECTRA's advantage is most pronounced at lower compute budgets. When you can afford to train for a long time (rightward on the x-axis), both objectives eventually converge to similar performance levels. When you have limited compute, the RTD advantage is dramatic. This is why the original ELECTRA paper emphasizes the efficiency framing: it speaks directly to the practitioners who cannot afford the compute budgets of large industrial research labs.
Key Parameters
When implementing RTD training, several parameters affect performance:
Several parameters interact to determine how well RTD training proceeds.
-
mask_prob is the fraction of tokens to mask before generating replacements. The default 0.15 (15%) balances training signal against context preservation. Higher rates provide more training examples but degrade generation quality: when too many tokens are masked, the generator has little context to work with and produces poor replacements. The 15% rate, which also works well for MLM, turns out to be well-calibrated for this reason.
-
disc_weight () is the weighting factor for the discriminator loss in the combined objective. ELECTRA uses 50, heavily prioritizing discriminator learning since it is the model used for downstream tasks. If is too small, the generator dominates gradient updates and the discriminator underfits. If is too large, the generator receives insufficient gradient and produces poor replacements, making the discriminator's task trivially easy.
-
generator_size_ratio is the ratio of generator to discriminator model size. Optimal values lie between 0.25 and 0.33. Smaller generators produce easily-detected replacements that do not challenge the discriminator enough, while larger generators waste parameters that could go toward discriminator capacity.
-
d_model (discriminator) is the hidden dimension of the discriminator transformer. Larger values increase capacity but require more compute. ELECTRA-Base uses 256, ELECTRA-Large uses 1024. Matching the discriminator's hidden dimension to the target task complexity is important: tasks requiring fine-grained semantic understanding benefit from larger hidden dimensions.
-
d_model (generator) is the hidden dimension of the generator, typically 1/4 to 1/3 of the discriminator's dimension. This asymmetry ensures the generator produces challenging but not impossible replacements.
-
n_layers (discriminator) is the number of transformer layers in the discriminator. More layers increase representational capacity. ELECTRA-Base uses 12 layers, ELECTRA-Large uses 24. The layer count can be kept equal between generator and discriminator even when the hidden dimension differs, as in the original ELECTRA design. This gives the generator enough depth to model context while keeping its parameter count low due to the smaller hidden dimension.
-
learning_rate can be set separately for generator and discriminator to improve training stability. Typical values range from 1e-4 to 5e-4, with some implementations using slightly lower rates for the generator to prevent it from improving too quickly and producing over-challenging replacements early in training.
-
temperature controls randomness when sampling from the generator's output distribution. Higher temperatures produce more diverse replacements by flattening the probability distribution, while lower temperatures favor the most likely tokens and produce less varied replacements. A temperature of 1.0 (the default, corresponding to unmodified softmax sampling) works well in practice.
Summary
Replaced token detection reformulates pretraining as a detection problem rather than a generation problem. This reformulation has one simple motivation (eliminate the 85% of wasted forward pass positions in MLM) and one key insight (detection is easier than generation, so the model can learn from every position without requiring the capacity needed for exact token prediction). Together, these produce a pretraining objective that trains encoders more efficiently than MLM across a wide range of compute budgets.
The key concepts from this chapter are:
- Generator-discriminator architecture uses a small network to produce replacement tokens and a larger network to detect them, with only the discriminator used for downstream tasks.
- Detection vs. generation is easier because binary classification requires less capacity than vocabulary prediction, enabling learning from every position.
- Sample efficiency improves by 6-7x because the discriminator loss applies to all positions rather than only the 15% that would be masked in MLM.
- Generator sizing at 1/4 to 1/3 of discriminator size balances challenging replacements against parameter efficiency.
- Weight sharing between generator and discriminator embeddings reduces parameters while maintaining compatible representations.
- Training dynamics create complementary learning where better generators produce harder replacements that train better discriminators.
- No adversarial training is needed: both networks optimize independent maximum likelihood objectives, making RTD more stable to train than GAN-based approaches despite the generator-discriminator framing.
ELECTRA's success with RTD demonstrated that the MLM paradigm, despite its widespread adoption, was not the most efficient path to strong language representations. The core ideas, assigning learning tasks to every input position and using detection rather than generation as the pretraining signal, have influenced subsequent work on efficient pretraining and continue to be relevant as the field explores better use of limited compute budgets.
The next chapter explores denoising objectives, a family of pretraining tasks that corrupt inputs in various ways and train models to reconstruct them.
Replaced Token Detection
Reference
Citation details
Cite or share this article.
Continue with the full handbook
This chapter is part of Language AI Handbook. Use the handbook page to browse the complete table of contents and continue reading in sequence.
Explore Language AI HandbookStay up to date
Get articles, book updates, and news delivered to your inbox.
No spam, unsubscribe anytime.
Join the community
Sign in to remove popups, track your reading progress, and join the discussion.
Comments
No comments yet. Be the first to share your thoughts!