Part of Language AI Handbook
Explains how BART trains language models using diverse text corruptions including token deletion, shuffling, sentence permutation.
Choose your expertise level to adjust how many terms are explained. Beginners see more tooltips, experts see fewer to maintain reading flow. Hover over underlined terms for instant definitions.
Article links
Make inline references clickable
Denoising Objectives
Language models learn by predicting missing or corrupted text. Masked language modeling replaces tokens with [MASK], and span corruption hides contiguous chunks. But what if we corrupted text in more diverse ways? Token deletion, shuffling, sentence permutation, and document rotation all introduce different types of noise that force models to learn different aspects of language structure.
Denoising objectives generalize the idea of text reconstruction. Instead of a single corruption strategy, they apply multiple transformations that break different properties of natural text. To recover the original, the model must learn word order, sentence boundaries, document structure, and semantic coherence. BART (Bidirectional and Auto-Regressive Transformers) pioneered this approach, showing that combining diverse noise types produces models that excel at both understanding and generation.
The core intuition behind this design is that different corruption types create different learning pressures. When you randomly mask a single token, you train the model to use local context to fill in a blank. But when you delete a token entirely, the model faces a harder challenge: it must figure out what word belongs there and where the gap is at all. When you permute sentences, you force the model to reason about causality, temporal sequence, and rhetorical flow at a level entirely beyond individual words. Each corruption type is essentially a different exam question testing a different facet of language understanding.
Think of it this way: a student who only ever practices fill-in-the-blank exercises will develop a narrow skill. A student who also practices reordering scrambled sentences, reconstructing documents from shuffled paragraphs, and expanding abbreviated summaries develops a much richer and more flexible understanding of how language works. The same principle applies to language model pretraining. By exposing the model to a diverse curriculum of reconstruction challenges, denoising objectives build representations that generalize across a wide range of downstream tasks.
In this chapter, we'll explore the major denoising transformations, understand what each one teaches the model, implement them from scratch, and see how combining them creates versatile language models.
The denoising autoencoder concept traces back to Vincent et al. (2008), who showed that training autoencoders to reconstruct clean data from corrupted inputs produced better feature representations than standard autoencoders. The key insight was that forcing a model to reconstruct from noise prevents trivial identity mappings and encourages the model to capture the underlying data distribution. Lewis et al. (2019) applied this principle to sequence-to-sequence language modeling at scale, combining it with an encoder-decoder transformer architecture to create BART. The result was a pretraining method that, unlike BERT, could be fine-tuned directly for text generation without architectural changes.
The Denoising Autoencoder Framework
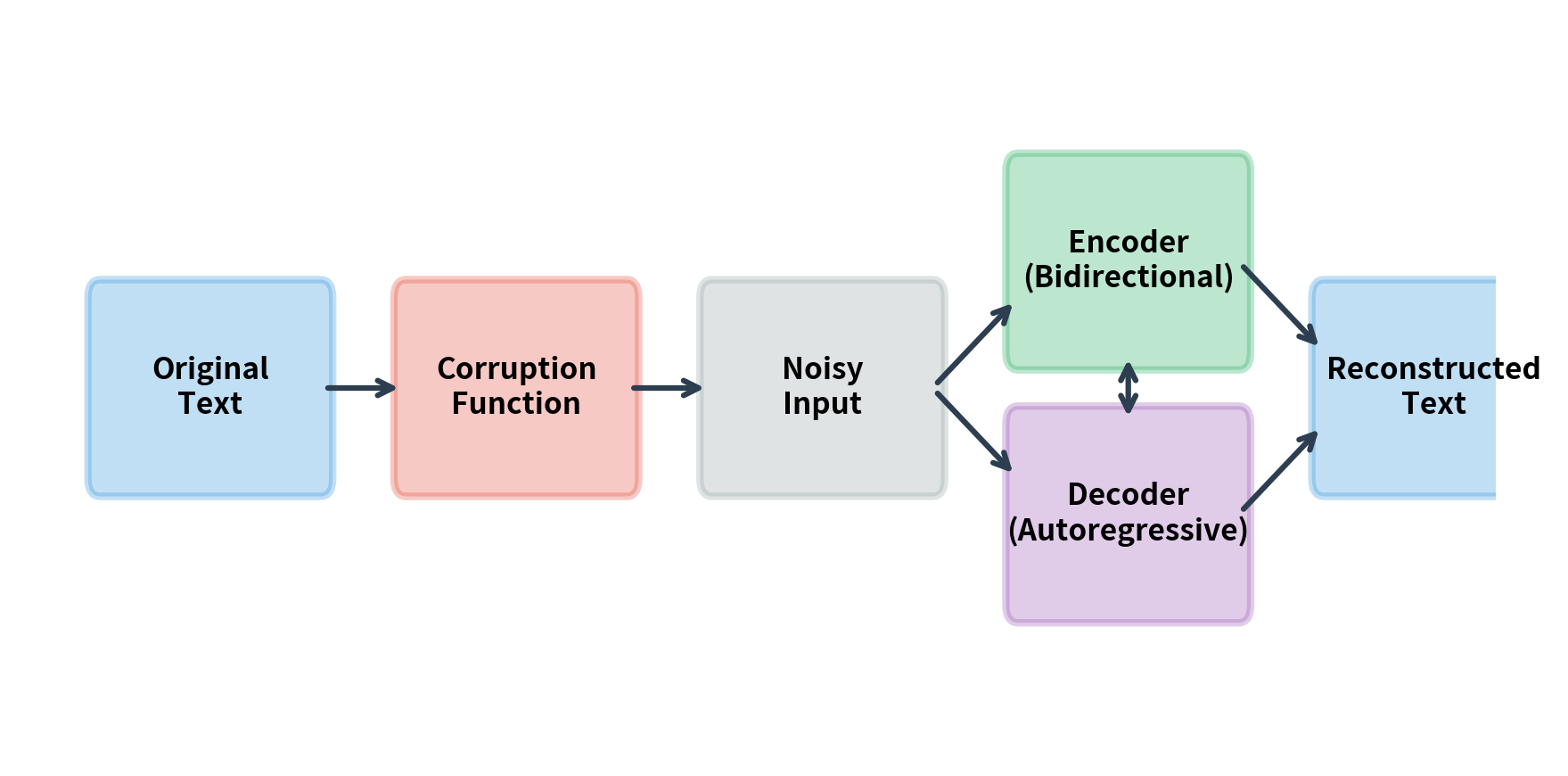
Denoising objectives treat pretraining as an autoencoding problem. The model receives corrupted input and must reconstruct the original. This differs from standard autoencoders, which simply copy input to output. By corrupting the input, we force the model to learn meaningful representations rather than trivial identity mappings.
A model trained to reconstruct clean data from corrupted inputs. By learning to remove noise, the model develops representations that capture the underlying structure of the data rather than surface-level patterns.
The key insight is that the corruption function acts as a form of regularization. If the model could see the clean input directly, it could achieve zero loss by copying the input to the output token by token, learning nothing useful in the process. By hiding part of the information, corruption forces the model to build internal representations that encode the meaning and structure of the text, because those representations are what allow it to fill in what is missing. This is analogous to how studying by closing your notes and trying to reconstruct key ideas is more effective than simply re-reading them.
Formally, given original text , we apply a corruption function to obtain noisy input . The model learns parameters to maximize the probability of recovering from . The training objective minimizes the negative log-likelihood of reconstructing the original:
where:
- : the denoising loss we want to minimize
- : the original, uncorrupted text sequence
- : the corrupted input produced by applying the corruption function to
- : the model parameters (encoder and decoder weights)
- : the probability the model assigns to the original text given the corrupted input
The negative log maps the probability (a value between 0 and 1) into a loss: when the model assigns high probability to the correct reconstruction, the loss is low. When the model is uncertain or wrong, the loss is high. Minimizing this loss trains the model to reliably reconstruct clean text from corrupted inputs.
The choice of corruption function determines what the model must learn. Simple corruptions like random token replacement teach local dependencies. Complex corruptions like document rotation teach global structure. By combining multiple corruption types, we can train models that understand language at every level.
The encoder-decoder architecture fits naturally with denoising. The encoder processes the corrupted input bidirectionally, building rich representations. The decoder generates the original text autoregressively, learning to produce coherent output. This combination gives BART-style models the best of both worlds: bidirectional encoding for understanding and autoregressive decoding for generation. Notice that this architectural choice is not arbitrary: the bidirectional encoder is necessary because reconstructing missing information often requires looking ahead as well as back. The autoregressive decoder is necessary because generating coherent text requires conditioning each output token on all previously generated tokens.
Token Deletion
Token deletion randomly removes tokens from the input sequence. Unlike masking, which replaces tokens with a placeholder, deletion removes them entirely. The model must determine which tokens are missing and where they belonged.
This corruption is more challenging than masking because position information is lost. With masking, the model knows exactly where each missing token should go because the [MASK] placeholder preserves the sequence length and signals the exact location of each gap. With deletion, the remaining tokens are simply concatenated without any placeholder marking where deletions occurred. The model must infer both the missing content and its correct location from context alone.
In practice, this means the model's decoder must learn to output a sequence longer than its encoder input. For masked language modeling, the input and output are always the same length. For token deletion, the output can be longer than the input by exactly the number of tokens that were removed. This length-expansion capability is particularly useful for tasks like abstractive summarization, where a short compressed input must be expanded into a longer and more detailed output.
def apply_token_deletion(tokens, deletion_prob=0.15):
"""
Delete tokens randomly from the sequence.
Args:
tokens: List of tokens
deletion_prob: Probability of deleting each token
Returns:
corrupted: Tokens with some deleted
original: Original tokens for reconstruction target
"""
corrupted = []
for token in tokens:
if np.random.random() > deletion_prob:
corrupted.append(token)
return corrupted, tokens# Demonstrate token deletion
original_sentence = "The quick brown fox jumps over the lazy dog".split()
deleted, target = apply_token_deletion(original_sentence, deletion_prob=0.2)Original (9 tokens): The quick brown fox jumps over the lazy dog After deletion (6 tokens): The quick brown fox lazy dog Deleted 3 tokens (33% of original)
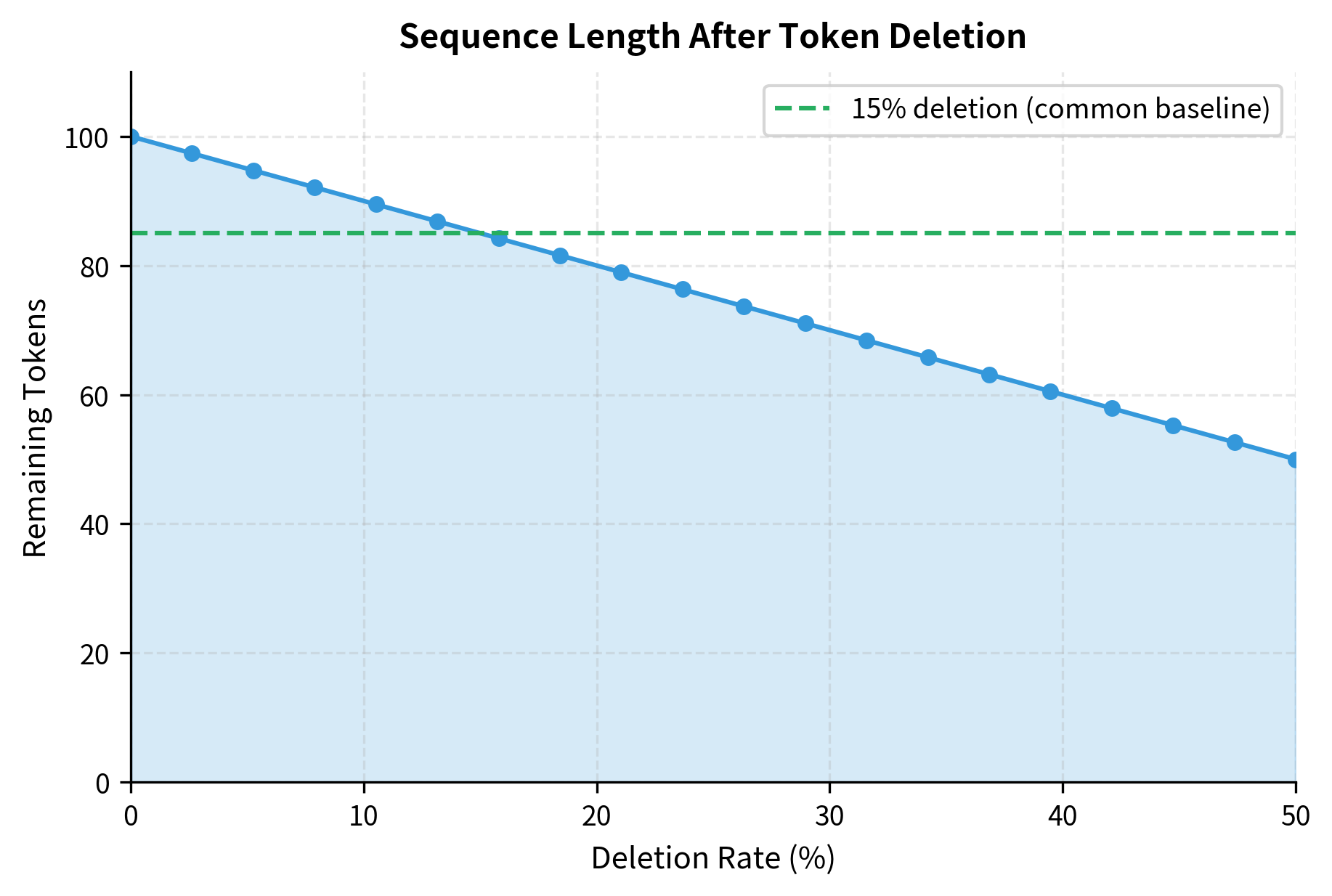
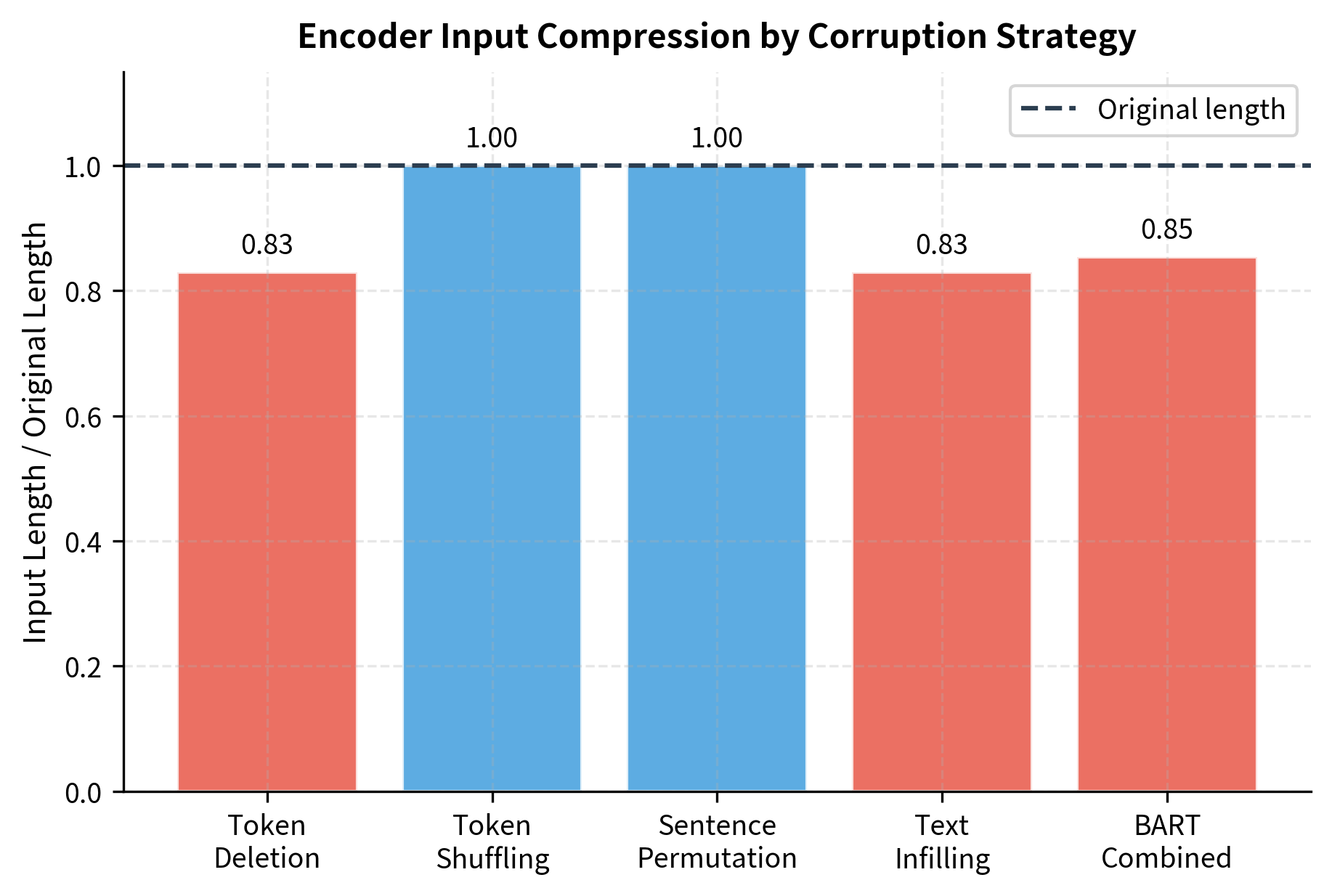
The corrupted sequence is shorter than the original. With a 20% deletion probability, we expect roughly 2 tokens to be removed from a 9-token sentence. The actual number varies due to random sampling. Notice that the deleted tokens could be anywhere in the sequence, and the remaining tokens are simply concatenated without any placeholder marking where deletions occurred. The model must learn to expand the sequence during reconstruction, inserting the missing tokens in the correct positions.
Token deletion teaches several important skills. First, the model learns less brittle representations that don't depend on specific tokens being present. Second, it learns about syntactic obligatoriness, recognizing when articles, prepositions, or other grammatical elements are missing. Third, it develops sensitivity to semantic completeness, detecting when content words have been removed. A sentence missing only function words ("quick brown fox jumps lazy dog") retains most of its meaning, while a sentence missing key content words ("The over the") loses its meaning almost entirely. Through many examples of both, the model learns which tokens carry the most informational weight.
Deletion Rate Selection
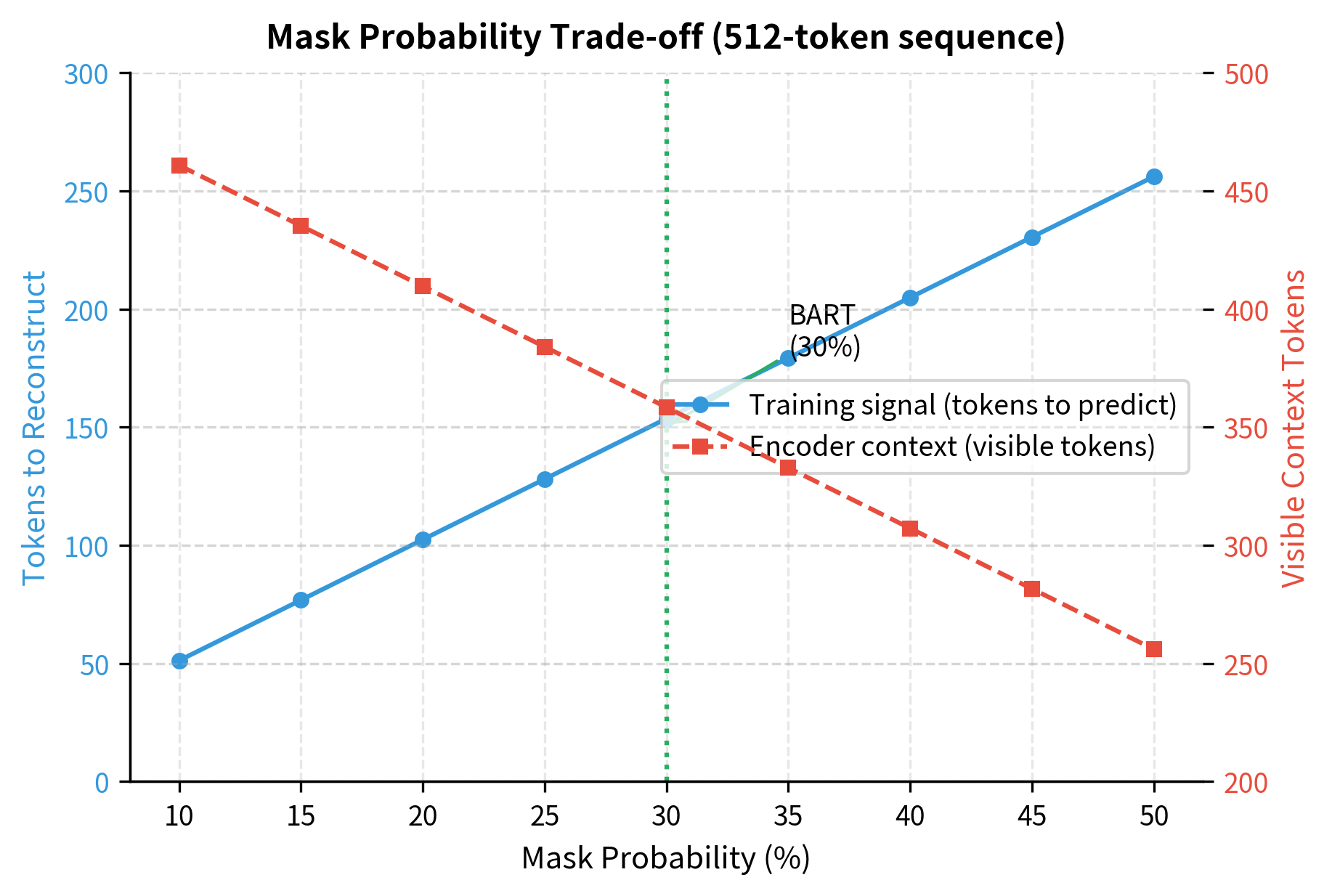
The deletion probability controls the difficulty of reconstruction. Too low (under 5%), and most sequences pass through unchanged. This provides little training signal. Too high (over 30%), and too much information is lost for reliable reconstruction.
A 15% deletion rate, matching BERT's masking rate, provides a reasonable balance. This removes enough tokens for meaningful learning while preserving sufficient context for accurate reconstruction. Note that BART's final configuration uses text infilling (30%) rather than pure token deletion, but 15% remains a common baseline when experimenting with deletion-based corruption. The BART paper found that pure token deletion performed worse than text infilling on generation tasks, because deletion alone doesn't train the model to handle variable-length gaps the same way that span-level masking does. However, deletion can be more effective than masking for tasks that specifically require understanding when information is absent rather than merely obscured.
Token Shuffling
Token shuffling permutes tokens within the sequence, breaking the original word order. The model must learn to reorder tokens into grammatically correct sequences. This corruption targets a model's understanding of syntax and word order constraints.
Unlike deletion, shuffling preserves all tokens. The information is present but scrambled. The model must learn that "dog the lazy" should become "the lazy dog" based on its understanding of English syntax. This is fundamentally a reordering problem rather than a reconstruction problem, and it requires the model to develop representations that encode syntactic roles, phrase structure, and the ordering constraints that govern natural language.
The key insight behind token shuffling is that it separates the questions of "what words are present" from "what order they should appear in." Because all the tokens are preserved, the model cannot fail the task by simply generating any plausible sentence. It must recover the specific original sentence from the scrambled version. This encourages the model to learn precise syntactic and semantic representations rather than vague semantic associations.
def apply_token_shuffling(tokens, shuffle_distance=3):
"""
Shuffle tokens within a limited distance of their original positions.
Args:
tokens: List of tokens
shuffle_distance: Maximum positions a token can move
Returns:
shuffled: Tokens with local shuffling applied
original: Original tokens for reconstruction target
"""
n = len(tokens)
# Add noise to positions, then sort
noisy_positions = np.arange(n) + np.random.uniform(0, shuffle_distance, n)
shuffle_order = np.argsort(noisy_positions)
shuffled = [tokens[i] for i in shuffle_order]
return shuffled, tokens# Demonstrate token shuffling
original_sentence = "The quick brown fox jumps over the lazy dog".split()
shuffled, target = apply_token_shuffling(original_sentence, shuffle_distance=3)Original: The quick brown fox jumps over the lazy dog Shuffled: quick The jumps brown fox over the lazy dog 5 of 9 tokens changed position (56%)
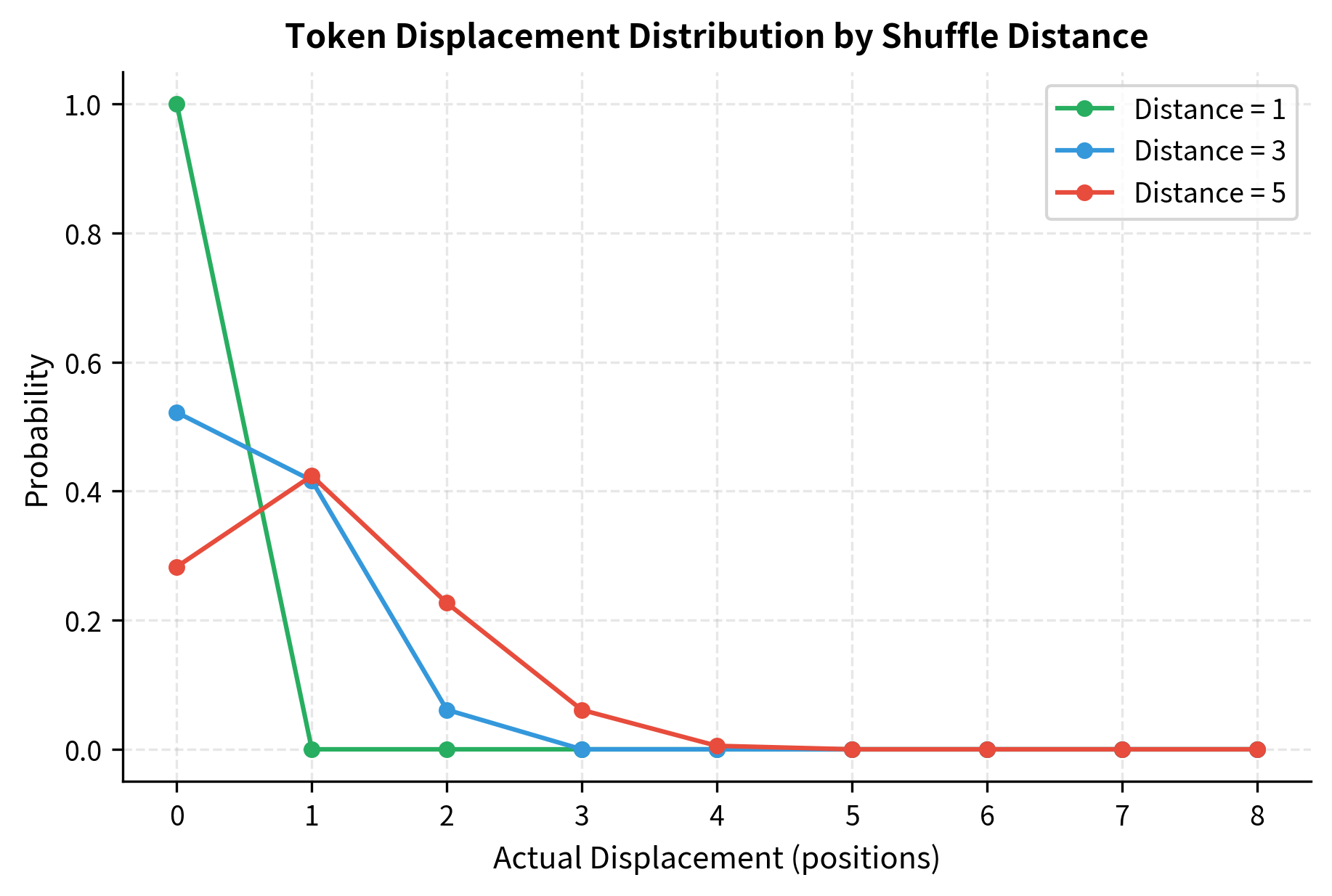
With a shuffle distance of 3, tokens can move up to 3 positions from their original location. The algorithm adds random noise to each position, then sorts by the noisy positions, creating local permutations while preserving rough ordering. This approach ensures that tokens tend to stay near their original positions rather than being scattered randomly across the entire sequence. The resulting corruption requires the model to recover syntactic order without making the task impossible.
Smaller distance values produce local permutations that are easier to correct. Larger values create more severe scrambling that requires understanding longer-range dependencies.
Local vs. Global Shuffling
Local shuffling (small distance) tests whether the model understands adjacent word relationships. Phrases like "the quick" or "brown fox" have strong local coherence that the model should detect. When a determiner appears after its noun, or an adjective after the word it modifies, the model must recognize the violation and correct it. This requires learning phrase-level syntactic patterns, the kinds of relationships that traditional n-gram models captured but that neural models can represent more flexibly.
Global shuffling (large distance) tests whether the model understands sentence-level structure. The subject-verb-object ordering of English, or the tendency for adjectives to precede nouns, becomes important when tokens move far from their original positions. A model that understands only local relationships can fix "the brown quick fox" to "the quick brown fox" but may struggle to reconstruct "jumps the fox over dog lazy the" because correcting it requires understanding the full argument structure of the sentence. Notice that the BART authors ultimately did not include token shuffling in their best-performing configuration, finding that it provided less benefit than text infilling for generation tasks, but it remains a useful diagnostic tool for understanding what ordering knowledge models acquire.
Sentence Permutation
Sentence permutation shuffles the order of sentences within a document. While token shuffling breaks word-level order, sentence permutation breaks discourse-level structure. The model must learn how sentences relate to each other and what ordering makes a coherent document.
This corruption helps with tasks that require understanding document structure, such as summarization, document classification, and multi-document reasoning. A model that can reconstruct a permuted document must understand individual sentences and the logical and temporal relationships that bind them into a coherent whole. This is qualitatively different from token-level understanding because it requires reasoning at the paragraph level about causal links and how ideas contrast, elaborate, or form a narrative arc.
Think of sentence permutation as training the model to become a skilled editor who can look at a jumbled set of sentences and recognize which one should come first, which provides necessary background information, and which is a conclusion that only makes sense after earlier evidence is established. In practice, this skill transfers directly to tasks like multi-document summarization, where the model must understand which pieces of information are foundational and which are elaborations, even when those pieces arrive from different sources in no particular order.
def apply_sentence_permutation(text, sentence_delimiter="."):
"""
Randomly permute sentences within the document.
Args:
text: Input text string
sentence_delimiter: Character that separates sentences
Returns:
permuted: Text with sentences reordered
original: Original text for reconstruction target
"""
# Split into sentences (keeping delimiter)
sentences = [
s.strip() + sentence_delimiter
for s in text.split(sentence_delimiter)
if s.strip()
]
# Random permutation
permuted_order = np.random.permutation(len(sentences))
permuted_sentences = [sentences[i] for i in permuted_order]
return " ".join(permuted_sentences), text# Demonstrate sentence permutation
document = "The cat sat on the mat. It was a sunny day. The cat fell asleep. Later it woke up hungry."
permuted, original = apply_sentence_permutation(document)Original document: The cat sat on the mat. It was a sunny day. The cat fell asleep. Later it woke up hungry. Permuted document: Later it woke up hungry. It was a sunny day. The cat sat on the mat. The cat fell asleep. 4 sentences randomly reordered
The permuted document contains all the original information but in scrambled order. Notice how "Later it woke up hungry" appears without prior context about the cat falling asleep, making the narrative harder to follow. The model must learn to detect these coherence breaks and recognize that certain sentences require prior context to make sense.
Discourse Coherence
Sentence permutation forces the model to learn discourse markers and rhetorical relationships. Words like "however," "therefore," "first," and "finally" provide strong signals about sentence ordering. Pronoun resolution also provides clues: "it" in "It was a sunny day" must refer to something previously mentioned. When "It was a sunny day" appears as the first sentence of the permuted document, the model must recognize that this anaphoric reference is stranded without its antecedent. The temporal adverb "Later" in "Later it woke up hungry" signals that this sentence describes an event that follows some earlier event, so it cannot possibly be the opening sentence of the document.
Narrative text is harder because events unfold in a specific order. Scientific writing with clear logical progression is easier because explicit markers guide the ordering. Creative writing with complex temporal structure is hardest because the "correct" order may not be unique. In practice, sentence permutation pretraining is most beneficial for tasks involving multi-sentence reasoning, like abstractive summarization of long documents, dialogue generation, and narrative question answering. The BART authors found that sentence permutation, combined with text infilling, gave the best overall performance across multiple evaluation benchmarks, suggesting that learning both local and discourse-level reconstruction is complementary rather than redundant.
Document Rotation
Document rotation moves a random portion of the document from the beginning to the end, or vice versa. The text is "rotated" around a randomly chosen pivot point. This corruption breaks the document's beginning and end while preserving internal structure.
The motivation for document rotation is somewhat different from the other corruptions. Where token deletion and sentence permutation test reconstruction of missing or reordered content, document rotation specifically trains sensitivity to document boundaries. Many text genres have highly stereotyped openings and closings: news articles begin with a lede, academic papers begin with an abstract and introduction, fairy tales begin with "Once upon a time," and legal documents begin with formal declarations. By forcing the model to recognize when these expected openings are missing and to identify where the true beginning of a document lies, rotation trains awareness of genre conventions and global document structure.
def apply_document_rotation(tokens):
"""
Rotate the document by moving tokens from the beginning to the end.
Args:
tokens: List of tokens
Returns:
rotated: Tokens with rotation applied
original: Original tokens for reconstruction target
rotation_point: Where the rotation occurred
"""
if len(tokens) < 2:
return tokens, tokens, 0
# Choose a random rotation point
rotation_point = np.random.randint(1, len(tokens))
# Rotate: move first part to the end
rotated = tokens[rotation_point:] + tokens[:rotation_point]
return rotated, tokens, rotation_point# Demonstrate document rotation
original_tokens = (
"Once upon a time there was a brave knight who lived in a castle".split()
)
rotated, original, pivot = apply_document_rotation(original_tokens)Original: Once upon a time there was a brave knight who lived in a castle Rotated at position 4 (29% into document): there was a brave knight who lived in a castle Once upon a time Moved to end: 'Once upon a time'
The rotated text starts mid-sentence with "was a brave knight..." rather than the natural opening "Once upon a time." The model must recognize this unnatural beginning and identify where the original document started. The classic fairy tale opening provides a strong signal about document structure, teaching the model to recognize common opening patterns like "Once upon a time," "In this paper," or "Chapter 1."
Start Token Identification
BART uses a special approach for document rotation: it always starts the corrupted input at a sentinel token that marks where the original document began. This simplifies the task slightly but still requires the model to learn document structure.
Without the sentinel, the model must learn to identify document beginnings from content alone. Phrases like "In this paper," "Chapter 1," or narrative openings like "It was a dark and stormy night" signal document starts. The model develops sensitivity to these patterns through the rotation objective. In practice, the document rotation objective showed smaller benefits than text infilling and sentence permutation in the BART ablation studies. However, it is valuable for domains where document structure is highly stereotyped, such as scientific literature or news, and for tasks like document beginning detection and coherence scoring.
def apply_document_rotation_with_sentinel(tokens, sentinel="[START]"):
"""
Rotate document and mark original start position with sentinel.
Args:
tokens: List of tokens
sentinel: Token to mark original document start
Returns:
rotated: Rotated tokens with sentinel marker
original: Original tokens
"""
if len(tokens) < 2:
return tokens, tokens
rotation_point = np.random.randint(1, len(tokens))
rotated = tokens[rotation_point:] + [sentinel] + tokens[:rotation_point]
return rotated, tokensrotated_with_sentinel, original = apply_document_rotation_with_sentinel(
original_tokens
)Original: Once upon a time there was a brave knight who lived in a castle Rotated with sentinel: in a castle [START] Once upon a time there was a brave knight who lived
The sentinel token provides an explicit signal about where rotation occurred. The model's job becomes somewhat easier: generate the correct sequence given knowledge of where the original start was.
Text Infilling
Text infilling combines aspects of span corruption and token deletion. Random spans of text are replaced with a single mask token, and the model must generate the missing content. Unlike span corruption where each span gets a unique sentinel, infilling uses a single mask token for all gaps.
This is more challenging than either simple masking or span corruption with unique sentinels because the model must determine both the content and the length of each missing span. A single [MASK] might represent one word or ten words. The model cannot treat each mask as a fixed-size prediction slot. Instead, it must learn to read the surrounding context and infer which words are missing and how many are missing. This length-prediction requirement is what makes text infilling so effective for training generation models: it forces the model to practice the same kind of variable-length expansion that it will need to perform during summarization, paraphrase generation, and story continuation.
The key insight is that text infilling trains the decoder to make length decisions. When generating text conditioned on a context, the model must decide how many tokens to produce before stopping. Standard autoregressive training on clean text teaches the model to produce a fixed target but doesn't specifically train it to infer the appropriate length from an incomplete input. Text infilling does exactly this, because every [MASK] token forces the model to decide: how many tokens does this gap need?
def apply_text_infilling(
tokens, mask_prob=0.15, mean_span_length=3, mask_token="[MASK]"
):
"""
Replace spans of tokens with a single mask token.
Args:
tokens: List of tokens
mask_prob: Probability of each token being in a masked span
mean_span_length: Average length of masked spans
mask_token: Token to insert for masked spans
Returns:
infilled: Tokens with spans replaced by mask tokens
original: Original tokens
spans: List of (start, end) tuples for masked spans
"""
n = len(tokens)
num_to_mask = int(n * mask_prob)
# Sample span lengths from geometric distribution
p = 1 / mean_span_length
spans = []
total_masked = 0
while total_masked < num_to_mask and len(spans) < n:
span_length = np.random.geometric(p)
span_length = min(span_length, num_to_mask - total_masked)
if span_length > 0:
spans.append(span_length)
total_masked += span_length
# Randomly place spans
mask = np.zeros(n, dtype=bool)
span_positions = []
for span_length in spans:
# Find valid start positions
valid_starts = []
for start in range(n - span_length + 1):
if not any(mask[start : start + span_length]):
valid_starts.append(start)
if not valid_starts:
continue
start = np.random.choice(valid_starts)
mask[start : start + span_length] = True
span_positions.append((start, start + span_length))
# Sort spans by position
span_positions.sort()
# Build infilled sequence
infilled = []
last_end = 0
for start, end in span_positions:
infilled.extend(tokens[last_end:start])
infilled.append(mask_token)
last_end = end
infilled.extend(tokens[last_end:])
return infilled, tokens, span_positionssentence = "The transformer architecture has revolutionized natural language processing".split()
infilled, original, spans = apply_text_infilling(
sentence, mask_prob=0.3, mean_span_length=2
)Original: The transformer architecture has revolutionized natural language processing Infilled: The transformer [MASK] revolutionized natural language processing Masked 2 tokens (25%) in 1 span(s): [2:4] 'architecture has' -> [MASK]
Multiple tokens collapse into single [MASK] placeholders. The 8-token sentence shrinks to fewer tokens because each span, regardless of length, becomes a single mask. The model must learn to generate the correct number of tokens for each mask, a more challenging objective than predicting a fixed number of tokens per placeholder.
Span Length Distribution
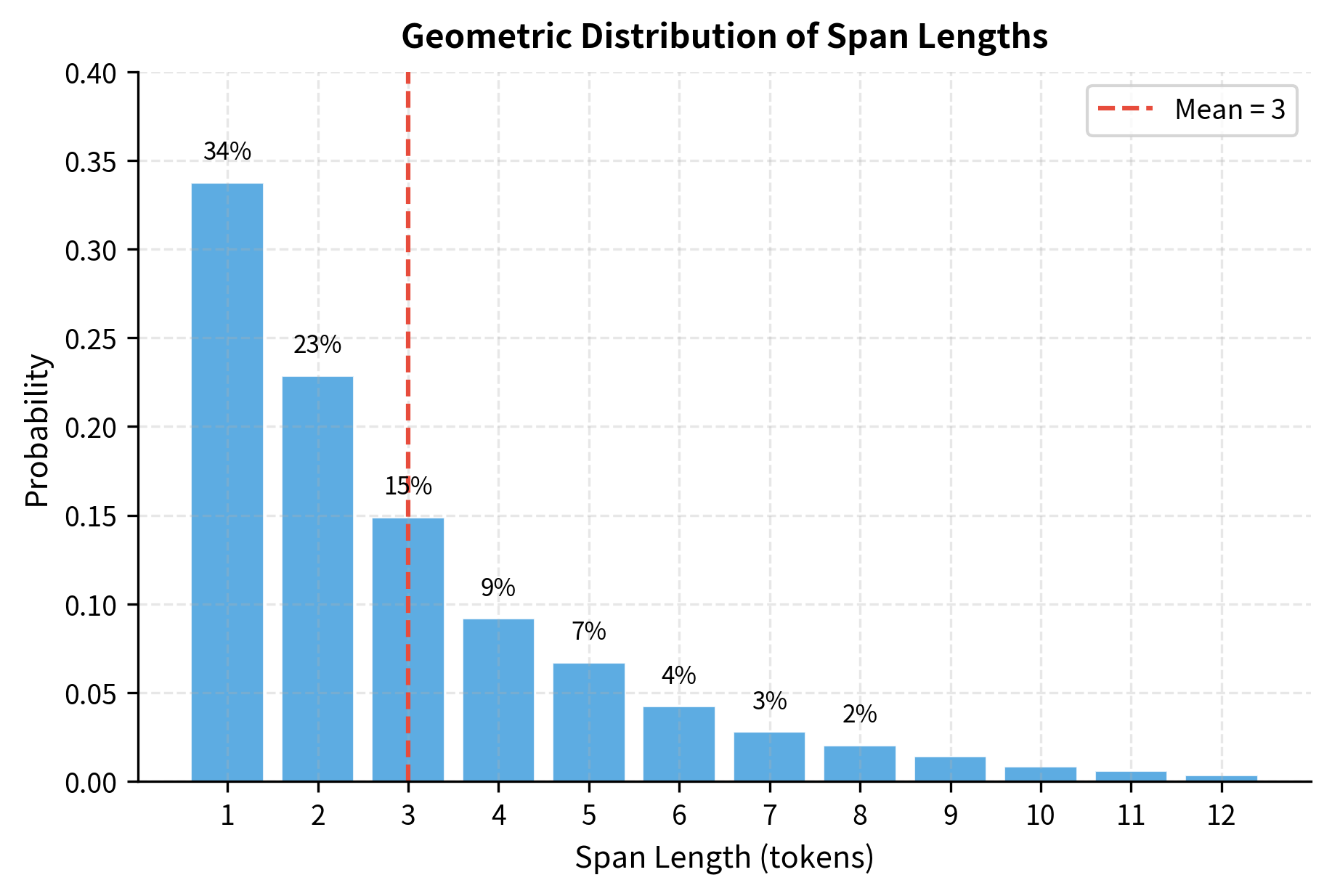
The geometric distribution controls how span lengths are sampled. With a mean of 3, most spans are short (1-2 tokens), but the heavy tail allows occasional longer spans that test phrase-level understanding.
The geometric distribution is a natural choice here because it has a memoryless property: the probability of a span having length given that it has length at least is constant. This means every additional token in a span is equally likely to be the last one, creating an exponentially decaying distribution of lengths. The parameter controls the rate of decay. A small produces a heavy-tailed distribution with many long spans, while a large produces mostly length-1 spans similar to standard token masking.
The distribution shows that roughly one-third of spans contain just a single token, similar to standard MLM. However, the remaining two-thirds contain multiple tokens, forcing the model to generate coherent phrases rather than isolated words. This balance between token-level and phrase-level prediction is key to text infilling's effectiveness. It ensures the model receives practice both at predicting individual words and at generating multi-word phrases and clauses, which is exactly what tasks like summarization and paraphrase generation require.
BART-Style Combined Denoising
BART combines multiple corruption types to create a versatile denoising objective. The original BART paper explored five transformations:
- Token masking: Replace tokens with
[MASK](similar to BERT) - Token deletion: Remove tokens entirely
- Text infilling: Replace spans with single
[MASK]tokens - Sentence permutation: Shuffle sentence order
- Document rotation: Rotate document around random point
The best-performing configuration used text infilling as the primary corruption, combined with sentence permutation. This combination forces the model to learn both local (word-level) and global (document-level) structure. Text infilling trains the decoder to generate variable-length continuations that fill in masked spans, which is a direct precursor to the generation capability needed for summarization. Sentence permutation trains the encoder to build representations that capture inter-sentence relationships, which supports tasks like coherence scoring and multi-document reasoning. Together, they ensure that neither local nor global language understanding is neglected during pretraining.
class BARTCorruptor:
"""
Apply BART-style denoising corruption to text.
Combines multiple corruption strategies:
- Text infilling (spans replaced with single mask)
- Sentence permutation (reorder sentences)
"""
def __init__(
self,
mask_prob=0.30,
mean_span_length=3,
permute_sentences=True,
mask_token="[MASK]",
):
self.mask_prob = mask_prob
self.mean_span_length = mean_span_length
self.permute_sentences = permute_sentences
self.mask_token = mask_token
def _split_sentences(self, tokens):
"""Split token list into sentences (simple period-based)."""
sentences = []
current = []
for token in tokens:
current.append(token)
if (
token.endswith(".")
or token.endswith("!")
or token.endswith("?")
):
sentences.append(current)
current = []
if current:
sentences.append(current)
return sentences
def _infill_tokens(self, tokens):
"""Apply text infilling to token list."""
n = len(tokens)
if n == 0:
return tokens
num_to_mask = max(1, int(n * self.mask_prob))
# Sample span lengths
p = 1 / self.mean_span_length
mask = np.zeros(n, dtype=bool)
span_positions = []
total_masked = 0
attempts = 0
while total_masked < num_to_mask and attempts < 100:
attempts += 1
span_length = np.random.geometric(p)
span_length = min(span_length, num_to_mask - total_masked, n)
valid_starts = [
i
for i in range(n - span_length + 1)
if not any(mask[i : i + span_length])
]
if not valid_starts:
continue
start = np.random.choice(valid_starts)
mask[start : start + span_length] = True
span_positions.append((start, start + span_length))
total_masked += span_length
span_positions.sort()
# Build result
result = []
last_end = 0
for start, end in span_positions:
result.extend(tokens[last_end:start])
result.append(self.mask_token)
last_end = end
result.extend(tokens[last_end:])
return result
def corrupt(self, tokens):
"""
Apply BART-style corruption.
Args:
tokens: List of string tokens
Returns:
dict with 'input' (corrupted) and 'target' (original) token lists
"""
working_tokens = list(tokens)
# Step 1: Sentence permutation (if enabled and multiple sentences)
if self.permute_sentences:
sentences = self._split_sentences(working_tokens)
if len(sentences) > 1:
order = np.random.permutation(len(sentences))
working_tokens = []
for i in order:
working_tokens.extend(sentences[i])
# Step 2: Text infilling
corrupted = self._infill_tokens(working_tokens)
return {"input": corrupted, "target": list(tokens)}# Demonstrate BART corruption
document = """The transformer changed NLP. Attention is all you need.
Models became larger. Performance improved dramatically."""
tokens = document.split()
corruptor = BARTCorruptor(
mask_prob=0.30, mean_span_length=3, permute_sentences=True
)
result = corruptor.corrupt(tokens)Original: The transformer changed NLP. Attention is all you need. Models became larger. Performance improved dramatically. Corrupted (13 tokens): Attention is all [MASK] need. Models became larger. The transformer changed [MASK] dramatically. Compression: 15 -> 13 tokens (13% reduction)
The corrupted version demonstrates both transformations working together. Sentences appear in a different order, and multiple spans have been replaced with [MASK] tokens. The sequence is noticeably shorter because each masked span, regardless of how many tokens it contained, becomes a single placeholder. This compression is a key efficiency advantage of text infilling: the encoder processes fewer tokens while the decoder still generates the full original.
The compression from text infilling provides computational savings during training. The encoder processes shorter sequences, reducing the quadratic attention cost, while the decoder still learns to generate the full original sequence. This asymmetry is intentional: it makes encoder computation cheap while keeping decoder training rich. For long documents, where encoder self-attention over the full sequence would be prohibitively expensive, this compression increases the number of training examples the model can process per hour.
Worked Example: Tracing a Single Document Through BART Corruption
To make the full pipeline concrete, let's trace a single document step by step through BART's combined corruption strategy and understand exactly what the model must learn at each stage.
Consider the following short document: "The sun rose over the mountains. The hikers began their ascent. By noon they reached the summit. The view was breathtaking."
This four-sentence document has a clear narrative structure: setting, action, culmination, reaction. The sentences flow logically from one to the next, with temporal markers ("By noon") and causal implications ("the view was breathtaking" follows "they reached the summit") binding them together.
When we apply sentence permutation, this document might become: "The view was breathtaking. The sun rose over the mountains. By noon they reached the summit. The hikers began their ascent." Now the reaction appears first, before the setting has been established. The temporal marker "By noon" loses its meaning because we haven't been told what morning activity the noon event follows. The document still contains all four sentences, but it no longer makes sequential sense.
Next, text infilling replaces 30% of the tokens with [MASK] placeholders using span lengths drawn from a geometric distribution. The permuted document might become: "The [MASK] breathtaking. The sun rose [MASK] mountains. By noon they [MASK] summit. The hikers [MASK] their ascent." Now the model faces a doubly corrupted input: the sentences are out of order, and each sentence has gaps of unknown length.
To reconstruct the original, the model must simultaneously: (1) recognize that the sentences are in the wrong order and reorder them as part of generating the target sequence, and (2) fill in the masked spans with the correct words and the correct number of words. The decoder must output "The sun rose over the mountains. The hikers began their ascent. By noon they reached the summit. The view was breathtaking." from the scrambled, gapped input.
This is an extraordinarily demanding task that requires the model to reason at multiple levels at once. Every training step on a document like this exercises the model's understanding of temporal sequence, discourse structure, argument structure within individual sentences, and the relationship between context and missing words. After seeing billions of such examples, the model develops the rich multi-level representations that make BART-style models effective across so many downstream tasks.
Comparing Corruption Strategies
Different corruptions teach different aspects of language understanding. Let's compare how each strategy transforms the same input.
def compare_corruptions(text, seed=42):
"""Compare all corruption strategies on the same text."""
tokens = text.split()
results = {}
# Token deletion
np.random.seed(seed)
deleted, _ = apply_token_deletion(tokens, deletion_prob=0.2)
results["Token Deletion"] = " ".join(deleted)
# Token shuffling
np.random.seed(seed)
shuffled, _ = apply_token_shuffling(tokens, shuffle_distance=3)
results["Token Shuffling"] = " ".join(shuffled)
# Text infilling
np.random.seed(seed)
infilled, _, _ = apply_text_infilling(
tokens, mask_prob=0.25, mean_span_length=2
)
results["Text Infilling"] = " ".join(infilled)
# Sentence permutation
np.random.seed(seed)
permuted, _ = apply_sentence_permutation(text)
results["Sentence Permutation"] = permuted
return resultssample = "The quick brown fox jumps. It leaps over the lazy dog. The dog wakes up surprised."
comparisons = compare_corruptions(sample)Original: The quick brown fox jumps. It leaps over the lazy dog. The dog wakes up surprised. ============================================================ Token Deletion: The quick brown fox over the lazy The dog wakes Token Shuffling: The quick brown jumps. fox It leaps over the dog. lazy wakes The dog up surprised. Text Infilling: The quick brown fox jumps. It leaps [MASK] [MASK] The dog wakes up surprised. Sentence Permutation: The quick brown fox jumps. It leaps over the lazy dog. The dog wakes up surprised.
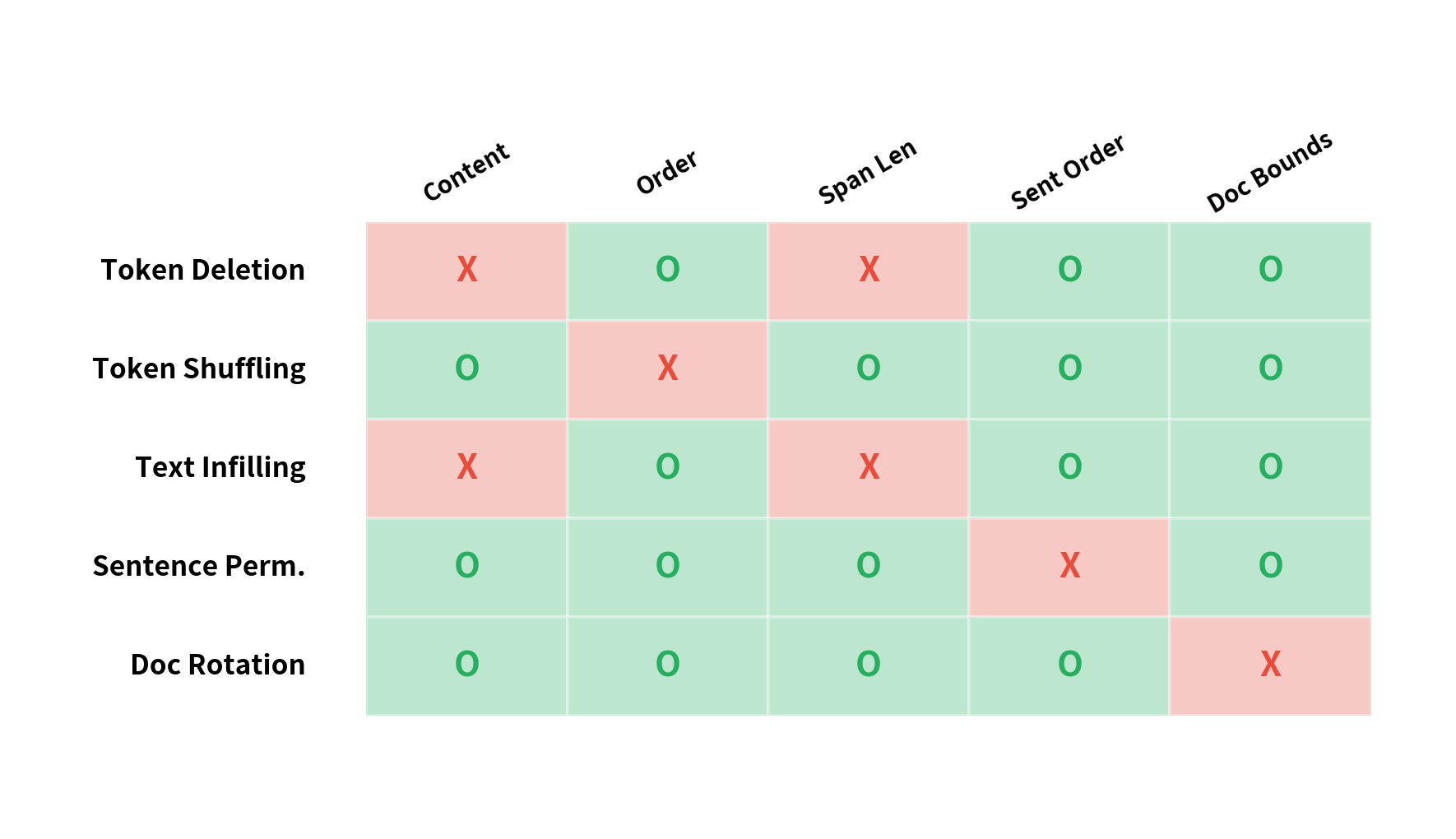
Each corruption breaks different properties:
- Token deletion: Removes specific words, breaking local completeness
- Token shuffling: Scrambles word order, breaking syntax
- Text infilling: Hides contiguous chunks, breaking both content and length
- Sentence permutation: Reorders sentences, breaking discourse flow
The choice of corruption depends on the target application. For generation tasks, text infilling works best because it trains the decoder to produce variable-length outputs. For understanding tasks, combining multiple corruptions teaches the model to recover several kinds of structure.
Training with Denoising Objectives
Training a denoising model requires carefully balancing the encoder and decoder. The encoder must build useful representations from corrupted input. The decoder must learn to generate coherent text conditioned on those representations.
The training setup is conceptually simple but hides important implementation details. On the encoder side, the corrupted sequence is padded to a fixed length and processed with full bidirectional attention, so every token can attend to every other token. The encoder produces a sequence of hidden states, one per input token, that capture contextual information about the corrupted document. On the decoder side, training uses teacher forcing: the decoder receives the ground-truth target tokens as input at each step and is trained to predict the next token. At inference time, teacher forcing is replaced by autoregressive generation, where each predicted token is fed back as input to predict the next one.
class DenoisingTrainer:
"""
Training loop for denoising language models.
Handles batching, corruption, and loss computation.
"""
def __init__(self, model, tokenizer, corruptor, learning_rate=1e-4):
self.model = model
self.tokenizer = tokenizer
self.corruptor = corruptor
self.optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
def prepare_batch(self, texts):
"""
Prepare a batch for training.
Args:
texts: List of text strings
Returns:
dict with encoder_input, decoder_input, labels tensors
"""
batch_encoder = []
batch_decoder = []
batch_labels = []
for text in texts:
tokens = text.split()
result = self.corruptor.corrupt(tokens)
# Corrupted text goes to encoder
encoder_tokens = result["input"]
# Original text is the target for decoder
target_tokens = result["target"]
batch_encoder.append(" ".join(encoder_tokens))
batch_decoder.append(" ".join(target_tokens))
batch_labels.append(" ".join(target_tokens))
return {
"encoder_texts": batch_encoder,
"decoder_texts": batch_decoder,
"target_texts": batch_labels,
}
def compute_loss(self, encoder_input, decoder_input, labels):
"""
Compute cross-entropy loss on target tokens.
This is a placeholder showing the structure.
Real implementation would use model forward pass.
"""
# In practice:
# outputs = self.model(encoder_input, decoder_input)
# loss = F.cross_entropy(outputs.logits, labels)
passThe training loop follows a straightforward sequence-to-sequence pattern:
- Sample a batch of documents from the training corpus
- Apply corruption (text infilling and sentence permutation)
- Pass corrupted input through the encoder
- Generate the original text with the decoder using teacher forcing
- Compute cross-entropy loss on target tokens
- Backpropagate gradients and update parameters
The training objective is standard sequence-to-sequence cross-entropy. The difference from other seq2seq tasks lies entirely in how the training pairs are constructed: the corrupted input is the source, and the original text is the target. This means you can use any standard seq2seq training infrastructure (Hugging Face Seq2SeqTrainer, for instance) and simply provide corrupted-original pairs as your dataset. The denoising is entirely a data preprocessing concern, not an architectural one.
Hyperparameter Considerations
Key hyperparameters for denoising pretraining include:
-
Mask probability (default: 30% for BART): Higher than BERT's 15% because infilling is more efficient. Each mask token can represent multiple original tokens.
-
Mean span length (default: 3): Balances short spans (token-level learning) with longer spans (phrase-level learning). Span lengths follow a geometric distribution with parameter , producing a mean of 3 tokens. Most spans are short (1-2 tokens), with occasional longer spans.
-
Sentence permutation probability: BART applies permutation to all documents. Some variants skip permutation for single-sentence inputs.
-
Learning rate: Standard transformer learning rates (1e-4 to 5e-4) with warmup work well.
-
Batch size: Large batches (2048+ tokens per GPU) help with the noisy gradients from aggressive corruption.
Limitations and Impact
Denoising objectives have transformed language model pretraining, but they come with tradeoffs that shape their practical applications.
The most fundamental limitation is the mismatch between pretraining and downstream tasks. During pretraining, the model always receives corrupted input and must produce the original. During fine-tuning and inference, the model receives clean input and must produce novel output. This gap means that denoising models may not immediately transfer their reconstruction skills to generation tasks without fine-tuning. BART addresses this partially through its autoregressive decoder, which learns generation patterns even during denoising, but the task distribution shift remains a concern for zero-shot applications. A model that has spent all of its pretraining learning to reconstruct from noise may not have developed the same degree of open-ended generative fluency as a model trained purely on next-token prediction over clean text.
Computational efficiency presents another tradeoff. Aggressive corruption reduces the input sequence length (especially with text infilling), which speeds up encoding. However, the decoder must still generate the full original sequence, and the encoder-decoder architecture is more expensive than encoder-only or decoder-only models of equivalent capacity. For pure understanding tasks, BERT-style encoders may be more efficient. For pure generation tasks, GPT-style decoders may be preferable. Denoising models like BART occupy a middle ground that excels when both capabilities are needed, such as in conditional text generation where the model must understand an input document and produce a coherent output based on it.
Key practical considerations include:
-
Corruption choice matters: Different corruptions suit different downstream tasks. Text infilling helps summarization but may not help classification. Empirical tuning is often necessary.
-
Sentence boundaries required: Sentence permutation requires reliable sentence segmentation. For domains with unusual punctuation or formatting, this corruption may introduce artifacts.
-
Length changes complicate batching: Token deletion and infilling change sequence lengths, requiring dynamic padding or variable-length batching infrastructure.
-
Hyperparameter sensitivity: The interaction between mask probability, mean span length, and sentence permutation means that the optimal corruption configuration varies by domain and downstream task. What works for news summarization may not be optimal for code generation or scientific question answering.
Despite these limitations, denoising objectives work well in practice. BART achieved state-of-the-art results on summarization and translation, as well as question answering, when released. The insight that diverse corruptions produce versatile models has influenced subsequent work like T5, mBART, and PEGASUS. Models trained with denoising objectives often transfer better to generation tasks than MLM-only models, while maintaining competitive understanding performance. The PEGASUS model, for instance, adapted the infilling idea specifically for summarization by masking entire sentences that were deemed important (using a sentence-level importance score), training the model to generate the most salient content from the remaining context. This shows how the general principle of denoising can be adapted and specialized for particular applications beyond what BART originally demonstrated.
Key Parameters
The corruption functions implemented in this chapter share several configurable parameters that control the difficulty and nature of the denoising task:
-
deletion_prob (default: 0.15): Probability of deleting each token in token deletion. Higher values remove more content but may destroy too much context for reliable reconstruction. The 15% rate matches BERT's masking rate, though BART's final model uses text infilling rather than pure deletion.
-
shuffle_distance (default: 3): Maximum positions a token can move during shuffling. Smaller values (1-2) test local word order, while larger values (5+) test sentence-level syntax understanding. The noise-based algorithm ensures tokens typically move less than the maximum.
-
mask_prob (default: 0.30 for BART): Fraction of tokens to include in masked spans during text infilling. Higher than BERT's 15% because each mask can represent multiple tokens, making the objective more efficient.
-
mean_span_length (default: 3): Average number of tokens per masked span. Sampled from a geometric distribution, meaning most spans are short (1-2 tokens) with occasional longer spans. Controls the balance between token-level and phrase-level learning.
-
permute_sentences (default: True): Whether to apply sentence permutation before text infilling. Combining both corruptions teaches both local and global structure. Can be disabled for single-sentence inputs.
-
mask_token (default: "[MASK]"): Placeholder token inserted for masked spans. Unlike span corruption which uses unique sentinels for each span, text infilling uses the same token for all spans, requiring the model to infer span boundaries.
Summary
Denoising objectives train models to reconstruct original text from corrupted inputs. By applying diverse corruption strategies, these objectives expose models to a rich curriculum of reconstruction challenges that build multi-level language understanding, from individual word choice to discourse-level coherence. This chapter covered the major corruption strategies and their effects:
-
Token deletion removes tokens entirely, forcing the model to identify missing content and insert it at the correct positions. Unlike masking, deletion also requires inferring the locations of gaps, making it a harder and more position-sensitive task.
-
Token shuffling permutes word order within a local window, teaching the model syntax and word order constraints. The shuffle distance controls whether the model focuses on local phrase structure or longer-range sentence organization.
-
Sentence permutation reorders sentences within documents, developing understanding of discourse structure and coherence. This corruption is uniquely effective for tasks that require reasoning about causality, temporal order, and rhetorical organization across multiple sentences.
-
Document rotation moves content from the beginning to the end, training sensitivity to document boundaries and openings. While showing smaller benefits than other corruptions in BART's ablation studies, it is particularly useful for genre-aware tasks.
-
Text infilling replaces spans with single mask tokens, combining content prediction with length prediction for flexible generation. The geometric distribution of span lengths ensures a mix of token-level and phrase-level reconstruction challenges.
-
BART-style combination uses text infilling plus sentence permutation to train models that excel at both understanding and generation. This combination covers both local and global structure, producing representations that transfer effectively to summarization and translation, as well as question answering.
The choice of corruption strategy depends on the target application. Text infilling suits generation tasks, while combining multiple corruptions produces general-purpose models that recover several kinds of structure. The encoder-decoder architecture of denoising models naturally supports both bidirectional encoding for understanding and autoregressive decoding for generation.
The next part of the book explores BERT and its variants, examining how encoder-only architectures apply masked language modeling to build powerful understanding models.
Denoising Objectives
Reference
Citation details
Cite or share this article.
Continue with the full handbook
This chapter is part of Language AI Handbook. Use the handbook page to browse the complete table of contents and continue reading in sequence.
Explore Language AI HandbookStay up to date
Get articles, book updates, and news delivered to your inbox.
No spam, unsubscribe anytime.
Join the community
Sign in to remove popups, track your reading progress, and join the discussion.
Comments
No comments yet. Be the first to share your thoughts!